Úloha 1J
Ak hranu kocky zväčšíme o 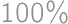 , tak o koľko percent sa zväčší jej objem?
, tak o koľko percent sa zväčší jej objem?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 2J
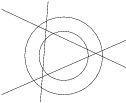
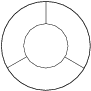
Najviac na koľko častí sa dá tromi priamkami rozdeliť medzikružie?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Chceme, aby všetky priesečníky priamok boli rôzne, ležali vo vnútri medzikružia a aby každá priamka bola sečnicou vnútorného kruhu. To sa nám podarí, ak vnútorná kružnica bude niečo medzi vpísanou a opísanou kružnicou trojuholníka, ktorý ohraničujú tri priamky.
Úloha 3J
Ak 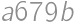 je päťciferné číslo deliteľné
je päťciferné číslo deliteľné 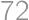 , zistite hodnotu súčinu
, zistite hodnotu súčinu 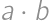 .
.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 4J
Učiteľ matematiky sa rozhodol usporiadať dve kolá minináboja päťčlenných družstiev vo svojej triede. V prvom kole sa žiaci rozdelili do družstiev ako chceli a v druhom kole ich učiteľ rozdelil tak, aby nikto nebol v družstve s nikým, s kým bol v družstve v prvom kole. Aký je najmenší počet žiakov, pre ktorý sa to učiteľovi vždy podarí?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Počet žiakov musí byť deliteľný 5. Ak by ich bolo 20 alebo menej, tak z Dirichletovho princípu aspoň dvaja žiaci, ktorí boli spolu v prvom kole, musia byť spolu aj v druhom. Našťastie 25 žiakov už stačí, lebo môžeme do každého nového družstva zobrať jedného z každého tímu.
Úloha 5J
Vanilkový koláč tvaru kvádra s rozmermi 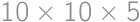 je na celom povrchu pokrytý tenkou vrstvou čokolády. Koláč rozrežeme na kocky
je na celom povrchu pokrytý tenkou vrstvou čokolády. Koláč rozrežeme na kocky 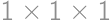 . Koľko percent kúskov nemá na sebe žiadnu čokoládu?
. Koľko percent kúskov nemá na sebe žiadnu čokoládu?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 6J
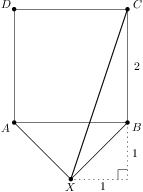
Majme štvorec 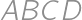 so stranou dĺžky
so stranou dĺžky 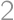 a bod
a bod 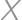 ležiaci mimo neho tak, že platí
ležiaci mimo neho tak, že platí 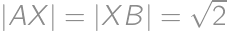 . Akú dĺžku má najdlhšia uhlopriečka päťuholníka
. Akú dĺžku má najdlhšia uhlopriečka päťuholníka 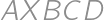 ?
?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 7J
V súčine 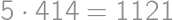 každú cifru zväčšite alebo zmenšite o 1 tak, aby bol výsledok správny. Aký bude výsledok?
každú cifru zväčšite alebo zmenšite o 1 tak, aby bol výsledok správny. Aký bude výsledok?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Stačí nám vyskúšať všetky možné zmeny na ľavej strane (je ich 16) a zisťovať, či sa dá pravá strana podľa toho zmeniť.
Úloha 8J
Pre celé čísla 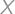 a
a 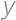 platí, že ich súčet je nanajvýš
platí, že ich súčet je nanajvýš 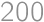 a ich rozdiel je menší ako
a ich rozdiel je menší ako 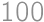 . Nájdite maximálnu hodnotu, ktorú môže nadobúdať výraz
. Nájdite maximálnu hodnotu, ktorú môže nadobúdať výraz 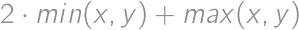 . Výraz
. Výraz 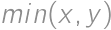 má hodnotu najmenšieho čísla z dvojice
má hodnotu najmenšieho čísla z dvojice 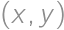 , podobne
, podobne 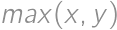 má hodnotu najväčšieho čísla z dvojice
má hodnotu najväčšieho čísla z dvojice 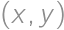 .
.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 9J
Pre reálne čísla 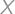 ,
, 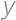 a
a 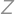 platí, že aritmetický priemer čísel
platí, že aritmetický priemer čísel 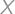 a
a 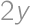 je rovný
je rovný 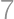 a aritmetický priemer čísel
a aritmetický priemer čísel 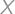 a
a 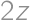 je rovný
je rovný 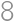 . Aký je aritmetický priemer čísel
. Aký je aritmetický priemer čísel 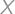 ,
, 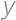 a
a 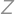 ?
?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Sčítaním prvých dvoch rovností pre aritmetický priemer 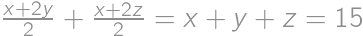 . Správny výsledok dostaneme predelením tejto rovnosti troma.
. Správny výsledok dostaneme predelením tejto rovnosti troma.
Úloha 10J
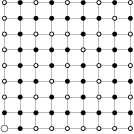
V mrežových bodoch štvorcovej mriežky 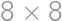 stojí 81 stromov. Záhradník vyrezal jeden z rohových stromov a teraz sa z jeho miesta pozerá na ostatné stromy. Niektoré však nevidí, pretože ich zakrývajú iné a to práve takto: strom
stojí 81 stromov. Záhradník vyrezal jeden z rohových stromov a teraz sa z jeho miesta pozerá na ostatné stromy. Niektoré však nevidí, pretože ich zakrývajú iné a to práve takto: strom 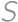 je zakrytý práve vtedy ak na úsečke medzi stromom
je zakrytý práve vtedy ak na úsečke medzi stromom 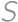 a záhradníkom leží iný strom, t.j. mrežový bod. Koľko stromov vidí záhradník?
a záhradníkom leží iný strom, t.j. mrežový bod. Koľko stromov vidí záhradník?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Nakreslíme si obrázok a postupne skontrolujeme stromy od tých, čo sú najbližšie k záhradníkovi, až po tie úplne najďalej. Kontrolovaný strom vždy označíme za viditeľný, ak ešte nebol vyškrtnutý a spolu s ním vyškrtneme všetky ďalšie stromy, ktoré tento strom zakrýva (ležia spolu s ním a záhradníkom na jednej priamke). Nakoniec spočítame všetky stromy, ktoré sme označili za viditeľné.
Úloha 11J / 1S
Koľkými spôsobmi vieme ofarbiť steny kocky čiernou a bielou farbou? Dve ofarbenia považujeme za rovnaké, ak dokážeme otočením jedného z nich dostať druhé.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Rozdeľme možnosti podľa toho, koľko stien zafarbíme bielou farbou. Pre nula stien máme jednu možnosť, rovnako ako pre jednu stenu. Pre dve steny existujú dve možnosti: zafarbené steny buď susedia jednou hranou, alebo sú protiľahlé. Pre tri steny sú tiež dve možnosti: Steny majú spoločný vrchol alebo dve sú protiľahlé a tretia susedí s obidvomi hranou. Pre štyri je rovnako veľa možností ako pre dve. Tak isto aj pre päť a šesť je toľko možností ako pre jednu a nula. Spolu všetkých možností je potom 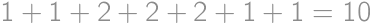 .
.
Úloha 12J / 2S
Majme obdĺžnik 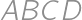 so stranami
so stranami 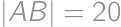 a
a 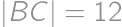 . Na polpriamke
. Na polpriamke 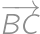 leží bod
leží bod 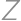 taký, že
taký, že 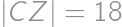 . Bod
. Bod 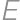 leží vo vnútri
leží vo vnútri 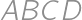 , pričom platí, že vzdialenosť
, pričom platí, že vzdialenosť 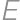 od
od 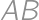 aj
aj 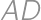 je
je 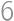 . Priamka
. Priamka 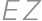 pretína strany
pretína strany 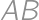 a
a 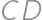 postupne v bodoch
postupne v bodoch 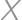 a
a 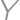 . Zistite obsah štvoruholníka
. Zistite obsah štvoruholníka 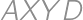 .
.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 13J / 3S
Pre koľko prirodzených čísel 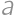 ,
,  , je číslo
, je číslo 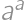 druhou mocninou prirodzeného čísla?
druhou mocninou prirodzeného čísla?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 14J / 4S
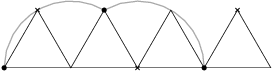
Majme rovnostranný trojuholník so stranou 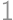 položený na podlahe. Jeden z jeho bodov zafarbíme na červeno. Trojuholník kotúľame po podlahe a trikrát ho preklopíme. Akú dlhú dráhu prejde červený bod?
položený na podlahe. Jeden z jeho bodov zafarbíme na červeno. Trojuholník kotúľame po podlahe a trikrát ho preklopíme. Akú dlhú dráhu prejde červený bod?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Uvedomíme si, že červený bod sa pohybuje po výsekoch kružnice (jeden bod vždy zostáva na mieste a vzdialenosť červeného bodu je od neho konštantná). Dvakrát prejde 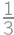 z obvodu kružnice a raz zostane na mieste. Dokopy prejde dráhu dĺžky
z obvodu kružnice a raz zostane na mieste. Dokopy prejde dráhu dĺžky 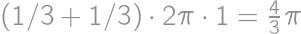 .
.
Úloha 15J / 5S
Aké je najmenšie kladné číslo zložené iba z núl a jednotiek, ktoré je deliteľné 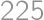 ?
?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 16J / 6S
Bill je dosť starý na to, aby volil, ale nie dosť na to, aby mohol využívať dôchodcovskú zľavu (jeho vek je medzi 18 a 70). Je o ňom známe, že pred 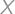 rokmi bol jeho vek odmocninou z jeho veku o
rokmi bol jeho vek odmocninou z jeho veku o  rokov. Billov vek je druhou mocninou prirodzeného čísla. Nájdite prirodzené číslo
rokov. Billov vek je druhou mocninou prirodzeného čísla. Nájdite prirodzené číslo 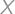 .
.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Billov vek, označme ho 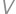 , je druhá mocnina prirodzeného čísla v rozpätí od 18 do 70. Ďalej vieme, že
, je druhá mocnina prirodzeného čísla v rozpätí od 18 do 70. Ďalej vieme, že 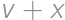 je taktiež druhou mocninou. Stačí vyskúšať niekoľko možností.
je taktiež druhou mocninou. Stačí vyskúšať niekoľko možností.
Úloha 17J / 7S
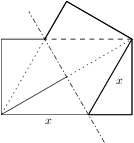
Priložme ľavý dolný roh obdĺžnikového papiera k pravému hornému rohu. Vznikne tak útvar rozdelený na tri trojuholníky, ktorých strany tvoria okraje papiera, a čiara zohnutia. Pre aký pomer dĺžok strán papiera je pomer obsahov týchto troch trojuholníkov 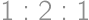 ?
?
Zobrazit / skrýt výsledek
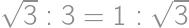 pripadne v opacnom poradi.
pripadne v opacnom poradi.
Úloha 18J / 8S
Koľko je trojciferných čísel deliteľných šiestimi, v ktorých je každá cifra väčšia ako 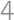 ?
?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
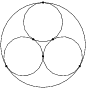
Úloha 19J / 9S
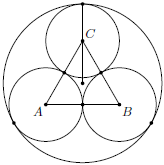
Dané sú tri kružnice s polomerom 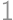 , pričom každé dve z nich sa navzájom zvonka dotýkajú. Týmto kružniciam opíšeme kružnicu
, pričom každé dve z nich sa navzájom zvonka dotýkajú. Týmto kružniciam opíšeme kružnicu 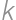 tak, aby sa jej zvnútra dotýkali všetky 3 kružnice. Vypočítajte polomer kružnice
tak, aby sa jej zvnútra dotýkali všetky 3 kružnice. Vypočítajte polomer kružnice 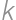 .
.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 20J / 10S
Nech  je prirodzené číslo. Ak
je prirodzené číslo. Ak 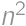 má cifru na mieste desiatok
má cifru na mieste desiatok 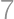 , akú cifru môže mať na mieste jednotiek?
, akú cifru môže mať na mieste jednotiek?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 21J / 11S
Ak napíšeme čísla 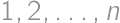 v nejakom poradí, získame tak
v nejakom poradí, získame tak  -reťazec. Napríklad, jeden z možných
-reťazec. Napríklad, jeden z možných  -reťazcov dĺžky 11 je:
-reťazcov dĺžky 11 je:
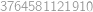
Aké je najmenšie
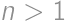
také, že existuje
 -reťazec,
-reťazec, ktorý je palindrómom (číta sa odpredu rovnako ako odzadu)?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Nasledujúci reťazec je takým 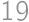 -reťazcom:
-reťazcom:
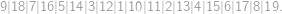
Ukážeme si, že 19 je najmenším takým číslom. Uvedomíme si, že iba jedno číslo sa môže vyskytnúť nepárny počet krát v palindromickom
 -reťazci
-reťazci (konkrétne stredná cifra). Ak
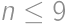 ,
, tak zrejme táto podmienka nie je splnená. Podobne, pre
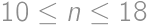
sa cifry
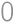
a
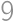
vyskytujú v reťazci práve raz, takže zase nemôže byť
 -reťazec
-reťazec palindrómom.
Úloha 22J / 12S
Nájdite všetky trojice 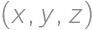 kladných reálnych čísel
kladných reálnych čísel 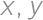 a
a 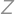 , pre ktoré platí
, pre ktoré platí 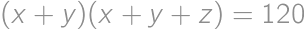 ,
, 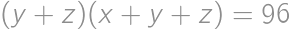 a
a 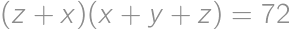 .
.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 23J / 13S
Majme kruh s polomerom 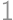 a v ňom dve kolmé tetivy, ktoré delia kruh na
a v ňom dve kolmé tetivy, ktoré delia kruh na 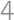 časti. Ofarbíme časť s najväčším a časť s najmenším obsahom čiernou, zvyšné necháme biele. Vieme, že obsah bielych častí bude taký ako obsah čiernych častí. Aká je maximálna možná vzdialenosť dlhšej tetivy od stredu kružnice?
časti. Ofarbíme časť s najväčším a časť s najmenším obsahom čiernou, zvyšné necháme biele. Vieme, že obsah bielych častí bude taký ako obsah čiernych častí. Aká je maximálna možná vzdialenosť dlhšej tetivy od stredu kružnice?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Stačí hľadať rovnaké obsahy. Napríklad ak rozrežeme kruh ešte dvoma tetivami, ktoré sú bodovo súmerné so stredom kružnice k pôvodným dvom tetivám, tak získame 9 častí, pričom stredná bude navyše. Preto musí aspoň jedna z priamok prechádzať stredom kružnice.
Úloha 24J / 14S
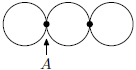
Strážnik má za úlohu strážiť tri objekty. Má obchôdzkové trasy ako na obrázku. Jedna obchôdzka začína v bode  , prejde cez každý úsek práve raz a vráti sa na začiatok. Ak záleží na smere obchádzania budovy, tak koľko rôznych obchôdzok existuje?
, prejde cez každý úsek práve raz a vráti sa na začiatok. Ak záleží na smere obchádzania budovy, tak koľko rôznych obchôdzok existuje?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Z bodu  má 4 možnosti kam sa vydať. Na najbližšej križovatke, kam sa dostane, má už len 2 možnosti (nemôže ísť naspäť ani dokončiť kolečko okolo prvej budovy). Na nasledujúcej križovatke má zas na výber 2 možnosti. Ďalej je už jeho cesta jednoznačne určená. Vyberal si zo
má 4 možnosti kam sa vydať. Na najbližšej križovatke, kam sa dostane, má už len 2 možnosti (nemôže ísť naspäť ani dokončiť kolečko okolo prvej budovy). Na nasledujúcej križovatke má zas na výber 2 možnosti. Ďalej je už jeho cesta jednoznačne určená. Vyberal si zo 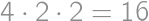 možných ciest.
možných ciest.
Úloha 25J / 15S
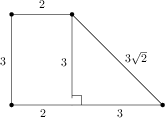
Lichobežník má strany dĺžky 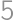 ,
, 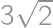 ,
, 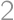 a
a 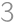 v tomto poradí, pričom rovnobežné sú strany dlhé
v tomto poradí, pričom rovnobežné sú strany dlhé 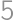 a
a 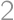 . Aký má obsah?
. Aký má obsah?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
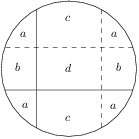
Úloha 26J / 16S
V rade za sebou stojí 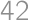 ľudí a chcú sa zoradiť podľa výšky tak, aby vpredu stál najvyšší. V jednom ťahu si môžu vymeniť miesto dvaja za sebou. Koľko najmenej ťahov potrebujú na to, aby sa týmto spôsobom zoradili, keď stoja na začiatku ľubovoľne?
ľudí a chcú sa zoradiť podľa výšky tak, aby vpredu stál najvyšší. V jednom ťahu si môžu vymeniť miesto dvaja za sebou. Koľko najmenej ťahov potrebujú na to, aby sa týmto spôsobom zoradili, keď stoja na začiatku ľubovoľne?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 27J / 17S
Petržlen žije v zeleninovom štáte, kde sa platí iba mincami v hodnote 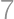 alebo
alebo 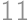 . Ak by mal Petržlen z oboch druhov mincí ľubovoľný počet, aká je najvyššia cena, ktorú nimi nevie zaplatiť?
. Ak by mal Petržlen z oboch druhov mincí ľubovoľný počet, aká je najvyššia cena, ktorú nimi nevie zaplatiť?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 28J / 18S
Rozdelíme kruh s polomerom 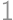 ľubovoľným spôsobom na štyri súvislé časti. Aký najmenší obvod môže mať časť s najväčším obsahom? Ak má viacero častí najväčší obsah, tak berieme tú s najmenším obvodom.
ľubovoľným spôsobom na štyri súvislé časti. Aký najmenší obvod môže mať časť s najväčším obsahom? Ak má viacero častí najväčší obsah, tak berieme tú s najmenším obvodom.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Najmenší možný obsah najväčšej časti je štvrtina obsahu kruhu. Súvislá časť s daným obsahom má najmenší obvod, ak má tvar kruhu. Takže ak rozsekneme pôvodný kruh tak, že všetky časti budú mať obsah práve štvrtinu obsahu pôvodného kruhu a jedna z tých častí bude mať kruhový tvar, tak sme hotoví. To sa dá napríklad vyseknutím sústrednej kružnice s pôvodným kruhom a polovičným polomerom a zvyšok rozrežeme na tri rovnaké časti ako na obrázku. Malá kružnica má obvod 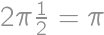 .
.
Úloha 29J / 19S
Nájdite súčet všetkých reálnych čísel 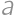 , pre ktoré majú rovnice
, pre ktoré majú rovnice 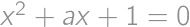 a
a 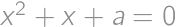 aspoň jeden spoločný reálny koreň.
aspoň jeden spoločný reálny koreň.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 30J / 20S
Koľko je takých osemciferných prirodzených čísel, že po škrtnutí ich prvej cifry zostane číslo 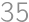 -krát menšie ako pôvodné?
-krát menšie ako pôvodné?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 31J / 21S
Máme pravouhlý trojuholník, ktorého všetky strany majú celočíselnú dĺžku. Ak má jedna z jeho strán dĺžku 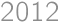 , aký môže mať najväčší obsah?
, aký môže mať najväčší obsah?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 32J / 22S
Nech 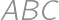 je trojuholník so stredom kružnice opísanej
je trojuholník so stredom kružnice opísanej 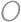 a priesečníkom výšok
a priesečníkom výšok  , pričom body
, pričom body 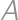 ,
, 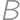 ,
, 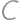 ,
, 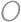 a
a  majú celočíselné súradnice a žiadne dva nesplývajú. Aký je druhý najmenší možný polomer kružnice opísanej trojuholníku
majú celočíselné súradnice a žiadne dva nesplývajú. Aký je druhý najmenší možný polomer kružnice opísanej trojuholníku 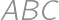 ?
?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 33J / 23S
Nájdite najväčšie prirodzené číslo  také, že číslo
také, že číslo 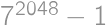 je deliteľné
je deliteľné 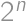 .
.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Viacnásobným použitím vzorca 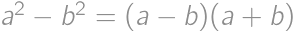 dostávame:
dostávame:
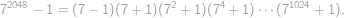
V rozvoji je každý z členov okrem
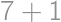
deliteľný 2 práve raz, čo sa dá jednoducho overiť skúmaním zvyškov
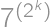
po delení 4.
Úloha 34J / 24S
Ak počítame súčin cifier daného čísla, potom súčin cifier tohto súčinu, potom znova súčin cifier nového súčinu atď., nutne po nejakom počte krokov dospejeme k jednocifernému číslu. Tento počet krokov nazývame vytrvalosťou čísla. Napr. číslo 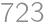 má vytrvalosť
má vytrvalosť 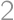 , lebo
, lebo 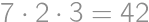 (1. krok) a
(1. krok) a 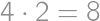 (2. krok). Nájdite najväčšie párne číslo s navzájom rôznymi nenulovými ciframi a vytrvalosťou
(2. krok). Nájdite najväčšie párne číslo s navzájom rôznymi nenulovými ciframi a vytrvalosťou 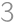 .
.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 35J / 25S
Ak strany 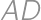 a
a 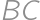 konvexného štvoruholníka
konvexného štvoruholníka 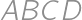 predĺžime, tak sa pretnú v bode
predĺžime, tak sa pretnú v bode 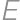 . Označme
. Označme  a
a 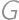 postupne stredy
postupne stredy 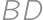 a
a 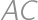 . Nájdite pomer obsahu trojuholníka
. Nájdite pomer obsahu trojuholníka 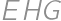 a obsahu štvoruholníka
a obsahu štvoruholníka 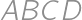 . Prezradíme vám, že tento pomer je rovnaký pre každý konvexný štvoruholník
. Prezradíme vám, že tento pomer je rovnaký pre každý konvexný štvoruholník 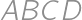 , ktorého strany
, ktorého strany 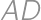 a
a 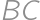 nie sú rovnobežné.
nie sú rovnobežné.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Pre prípad, že 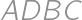 je rovnoramenný lichobežník so stranami 1, 1, 1 a
je rovnoramenný lichobežník so stranami 1, 1, 1 a 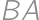 = 2, to vychádza ľahko aj bez väčšieho počítania, keďže je tam veľa rovnostranných trojuholníkov. V riešení pre všeobecný prípad budeme
= 2, to vychádza ľahko aj bez väčšieho počítania, keďže je tam veľa rovnostranných trojuholníkov. V riešení pre všeobecný prípad budeme 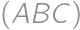 označovať obsah
označovať obsah 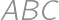 . Dokreslime si úsečky
. Dokreslime si úsečky 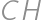 ,
, 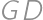 ,
, 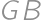 . Keďže
. Keďže 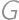 je stred
je stred 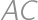 , tak
, tak 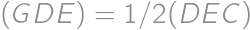 . Podobne
. Podobne 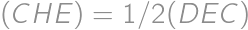 . Teda
. Teda 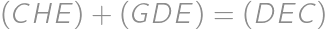 . Z toho vieme usúdiť, že
. Z toho vieme usúdiť, že 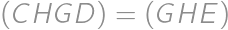 . Keďže
. Keďže 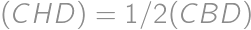 a
a 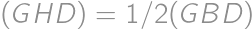 , tak
, tak 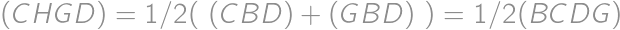 . Ale
. Ale 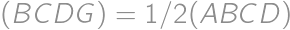 , lebo
, lebo 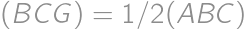 a
a 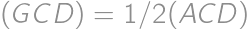 . Potom
. Potom 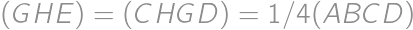 .
.
Úloha 36J / 26S
Kockaté termity vyvŕtali cez kocku so stranou 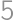 v každom smere štyri rovné chodbičky ako na obrázku a opustili ju. To, čo z kocky zostalo, chceme ofarbiť antitermitovou farbou. Koľko centimetrov štvorcových musíme ofarbiť?
v každom smere štyri rovné chodbičky ako na obrázku a opustili ju. To, čo z kocky zostalo, chceme ofarbiť antitermitovou farbou. Koľko centimetrov štvorcových musíme ofarbiť?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 37J / 27S
Máme kruh s polomerom 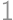 a stojíme na najľavejšom bode jeho obvodu. Môžeme sa hýbať len doprava a hore. Akú dĺžku má najdlhšia trasa, ktorú môžeme prejsť, ak nechceme z kruhu vyjsť?
a stojíme na najľavejšom bode jeho obvodu. Môžeme sa hýbať len doprava a hore. Akú dĺžku má najdlhšia trasa, ktorú môžeme prejsť, ak nechceme z kruhu vyjsť?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 38J / 28S
Aký je najväčší deliteľ čísla 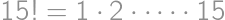 taký, že po vydelení
taký, že po vydelení 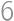 dáva zvyšok
dáva zvyšok 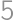 ?
?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 39J / 29S
Máme kocku a v nej nasledovných 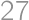 bodov: vrcholy kocky, stredy hrán, stredy stien a stred kocky. Koľko je priamok, ktoré prechádzajú práve cez tri body?
bodov: vrcholy kocky, stredy hrán, stredy stien a stred kocky. Koľko je priamok, ktoré prechádzajú práve cez tri body?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Rozdelíme si všetky priamky do troch nezávislých kategórií. Tých, ktoré prechádzajú stredom kocky, je 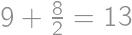 . Tých, ktoré prechádzajú stredom steny a neprechádzajú stredom kocky, je pre každú stenu 4 a dokopy teda 24. Zvýšili nám už len priamky totožné s hranami kocky, ktorých je 12. Dokopy máme
. Tých, ktoré prechádzajú stredom steny a neprechádzajú stredom kocky, je pre každú stenu 4 a dokopy teda 24. Zvýšili nám už len priamky totožné s hranami kocky, ktorých je 12. Dokopy máme 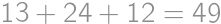 priamok.
priamok.
Úloha 40J / 30S
Sútaže trvajúcej 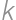 dní sa zúčastnilo
dní sa zúčastnilo  účastníkov. Každý deň všetci účastníci získali skóre
účastníkov. Každý deň všetci účastníci získali skóre 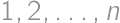 bodov, pričom žiadni dvaja nemali rovnaký počet bodov za daný deň. Na konci súťaže (
bodov, pričom žiadni dvaja nemali rovnaký počet bodov za daný deň. Na konci súťaže (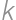 -ty deň večer po súťaži) mal každý účastník v súčte za všetky dni skóre
-ty deň večer po súťaži) mal každý účastník v súčte za všetky dni skóre 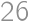 bodov. Nezávisle od
bodov. Nezávisle od 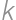 , nájdite súčet všetkých
, nájdite súčet všetkých  , pre ktoré je to možné.
, pre ktoré je to možné.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 41J / 31S
Máme tortu, ktorú chceme rozrezať. Torta má tvar valca a každý rez má tvar roviny. Napríklad dvoma rezmi ju vieme rozrezať na štyri časti a troma rezmi na osem častí. Na koľko najviac častí ju vieme rozrezať piatimi rezmi?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 42J / 32S
Osemramenná hviezda je teleso, ktoré vznikne prilepením pravidelných štvorstenov na všetky steny pravidelného osemstena. Hrany osemstena aj všetkých štvorstenov majú dĺžku 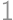 . Aký objem má osemramenná hviezda?
. Aký objem má osemramenná hviezda?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 43J / 33S
Stopár ide po ceste. Šanca, že v najbližších 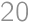 minútach stretne auto je
minútach stretne auto je 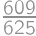 . Ak je v každom okamihu rovnaká šanca, že stretne auto, tak aká je šanca, že stretne auto v najbližších piatich minútach?
. Ak je v každom okamihu rovnaká šanca, že stretne auto, tak aká je šanca, že stretne auto v najbližších piatich minútach?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 44J / 34S
Vandal a moderátor upravujú článok na Wikipédii. Na začiatku bol článok bez chyby a každý deň vandal pridal jeden chybný údaj. Na konci každého dňa má moderátor 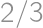 šancu na nájdenie každej jednotlivej chyby, ktorá ešte v článku je. Aká je šanca, že po troch dňoch bude článok bezchybný?
šancu na nájdenie každej jednotlivej chyby, ktorá ešte v článku je. Aká je šanca, že po troch dňoch bude článok bezchybný?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 45J / 35S
Máme k dispozícii neobmedzenú zásobu červených, modrých a žltých kariet. Za každú kartu sa dostávajú body, a to nasledovne:
- za každú červenú kartu je jeden bod
- za každú modrú kartu je toľko bodov, koľko je dvojnásobok počtu našich červených kariet
- za každú žltú kartu je toľko bodov, koľko je trojnásobok počtu našich modrých kariet
Koľko najviac bodov dokážeme získať pomocou pätnástich kariet?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 46J / 36S
Matúš má jednu 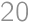 -stennú hraciu kocku a CDčko má tri
-stennú hraciu kocku a CDčko má tri 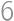 -stenné hracie kocky. Aká je šanca, že po hodení kockami bude hodnota na Matúšovej kocke väčšia, ako súčet hodnôt na CDčkových kockách?
-stenné hracie kocky. Aká je šanca, že po hodení kockami bude hodnota na Matúšovej kocke väčšia, ako súčet hodnôt na CDčkových kockách?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Uvedomíme si, že oba hody majú symetrické rozdelenie. Tj. pravdepodobnosť, že padne 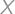 na dvadsaťstennej je rovnaká, ako že padne
na dvadsaťstennej je rovnaká, ako že padne 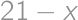 (od 1 po 20). A podobne pravdepodobnosť, že padne
(od 1 po 20). A podobne pravdepodobnosť, že padne 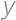 na troch šesťstenných, je rovnaká, ako že padne
na troch šesťstenných, je rovnaká, ako že padne 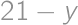 (od 3 po 18). Podobnou úvahou zistíme, že pravdepodobnosť výhry Matúša je rovnaká, ako pravdepodobnosť výhry CDčka. Preto je výsledok
(od 3 po 18). Podobnou úvahou zistíme, že pravdepodobnosť výhry Matúša je rovnaká, ako pravdepodobnosť výhry CDčka. Preto je výsledok 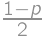 kde
kde 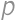 je pravdepodobnosť remízy. A tá je
je pravdepodobnosť remízy. A tá je 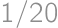 , keďže nech hodí CDčko troma kockami ľubovoľnú hodnotu, tak Matúš má vždy šancu
, keďže nech hodí CDčko troma kockami ľubovoľnú hodnotu, tak Matúš má vždy šancu 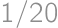 , aby ju trafil.
, aby ju trafil.
Úloha 47J / 37S
Majme tabuľku 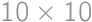 . Riadky, resp. stĺpce očíslujeme postupne zľava doprava resp. zhora, dole číslami od
. Riadky, resp. stĺpce očíslujeme postupne zľava doprava resp. zhora, dole číslami od 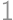 po
po 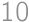 . Do každého políčka vpíšeme súčin čísla riadku a čísla stĺpca, v ktorom sa nachádza. Stanka stojí na políčku v ľavom hornom rohu a chce sa dostať na políčko v pravom dolnom rohu. Stanka môže chodiť iba doprava a dole (šikmo nie). Stankine číslo je súčinom čísel na políčkach, na ktoré Stanka stúpila (vrátane prvého a posledného). Ak uvažujeme všetky možné Stankine čísla, aký je ich najväčší spoločný deliteľ?
. Do každého políčka vpíšeme súčin čísla riadku a čísla stĺpca, v ktorom sa nachádza. Stanka stojí na políčku v ľavom hornom rohu a chce sa dostať na políčko v pravom dolnom rohu. Stanka môže chodiť iba doprava a dole (šikmo nie). Stankine číslo je súčinom čísel na políčkach, na ktoré Stanka stúpila (vrátane prvého a posledného). Ak uvažujeme všetky možné Stankine čísla, aký je ich najväčší spoločný deliteľ?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 48J / 38S
Majme trojuholník s výškami dlhými 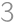 ,
, 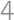 a
a 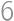 . Aký je jeho obvod?
. Aký je jeho obvod?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 49J / 39S
Nájdite najväčšie prirodzené číslo 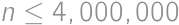 , pre ktoré je výraz
, pre ktoré je výraz 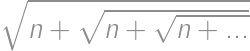 racionálny.
racionálny.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Označme  . Potom platí
. Potom platí 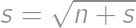 . Riešením kvadratickej rovnice pre
. Riešením kvadratickej rovnice pre 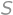 je
je 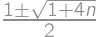 , a keďže
, a keďže 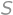 má byť racionálne, tak musí
má byť racionálne, tak musí 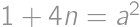 , kde
, kde 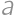 je racionálne číslo. Úpravou výrazu dostaneme
je racionálne číslo. Úpravou výrazu dostaneme 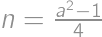 . Aby bolo
. Aby bolo  celé, musí byť aj
celé, musí byť aj 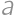 celé, pretože ak
celé, pretože ak 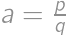 je vykrátený zlomok, tak
je vykrátený zlomok, tak 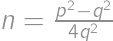 má byť celé číslo, a teda
má byť celé číslo, a teda 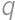 by muselo deliť
by muselo deliť 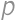 , čo je spor s vykráteným zlomkom. Ďalšou úpravou máme
, čo je spor s vykráteným zlomkom. Ďalšou úpravou máme 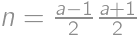 , a teda
, a teda 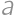 musí byť nepárne a aby
musí byť nepárne a aby 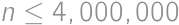 , tak najväčšie
, tak najväčšie 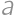 získame keď
získame keď 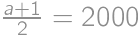 , z čoho
, z čoho 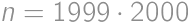 .
.
Úloha 50J / 40S
Majme Maxištvorec 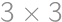 tvorený deviatimi štvorcovými kachličkami. Každá kachlička je rozdelená na štyri rovnaké štvorčeky, v ktorých sú vpísané čísla
tvorený deviatimi štvorcovými kachličkami. Každá kachlička je rozdelená na štyri rovnaké štvorčeky, v ktorých sú vpísané čísla 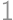 ,
, 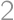 ,
, 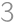 a
a 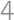 (každé práve raz). Dve kachličky sa môžu dotýkať len rovnakými číslami (ako dominá). Koľko rôznych Maxištvorcov existuje?
(každé práve raz). Dve kachličky sa môžu dotýkať len rovnakými číslami (ako dominá). Koľko rôznych Maxištvorcov existuje?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Kachličku vľavo si pevne zvolíme (1,2 a 3,4). Uvedomíme si, že celá situácia záleží len na štyroch kľúčových hodnotách. Nech ľavé horné políčko má súradnice 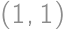 , tak kľúčové sú
, tak kľúčové sú 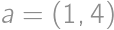 ,
, 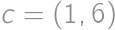 ,
, 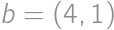 a
a 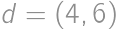 . Do každej z nich môžu byť vpísané len 2 čísla, takže máme maximálne
. Do každej z nich môžu byť vpísané len 2 čísla, takže máme maximálne 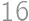 možností. Treba si uvedomiť, že nevyhovujú všetky, niekedy príde ku kolíziám vo vnútri. Takže buď ich všetky vyskúšame, alebo pracujeme s označenými hodnotami
možností. Treba si uvedomiť, že nevyhovujú všetky, niekedy príde ku kolíziám vo vnútri. Takže buď ich všetky vyskúšame, alebo pracujeme s označenými hodnotami 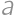 ,
,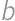 ,
,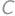 a
a 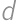 a prídeme na nejaké vzťahy. Napríklad nesmie byť
a prídeme na nejaké vzťahy. Napríklad nesmie byť 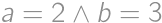 kvôli strednej kachličke,
kvôli strednej kachličke, 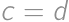 kvôli pravej dolnej,
kvôli pravej dolnej,  kvôli pravej strednej a
kvôli pravej strednej a 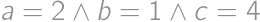 kvôli strednej dolnej. To nám dokopy vylúči 9 možností (jednu sme zarátali dvakrát). Nezabudnime výsledok vynásobiť 24 — toľko je možností ako môže vyzerať prvá kachlička.
kvôli strednej dolnej. To nám dokopy vylúči 9 možností (jednu sme zarátali dvakrát). Nezabudnime výsledok vynásobiť 24 — toľko je možností ako môže vyzerať prvá kachlička.
Úloha 51J / 41S
Ondro svoje obľúbené číslo (zapísané v desiatkovej sústave a bez nuly na začiatku) nazýva balónik. Pre balónik platí:
- Číslo o 1 väčšie ako balónik je deliteľné 210.
- Ciferný súčet balónika je dvojnásobok počtu jeho cifier.
- Balónik nemá viac ako 12 cifier.
- Cifry balónika sú na striedačku párne a nepárne (balónik nemusí začínať párnou cifrou).
Určite hodnotu Ondrovho balónika.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Zameriame sa na podmienku, že číslo o 1 väčšie je deliteľné 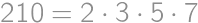 . Z toho je hneď zrejmé, že posledná cifra musí byť 9. Kvôli deliteľnosti trojkou je ciferný súčet tvaru
. Z toho je hneď zrejmé, že posledná cifra musí byť 9. Kvôli deliteľnosti trojkou je ciferný súčet tvaru 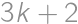 . Zo zadania ciferný súčet balónika je dvojnásobok počtu jeho cifier. Ciferné súčty, keďže sú párne, tvaru
. Zo zadania ciferný súčet balónika je dvojnásobok počtu jeho cifier. Ciferné súčty, keďže sú párne, tvaru 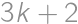 a väčšie ako 9, prichádzajú do úvahy 14 a 20. Im zodpovedajú počty cifier
a väčšie ako 9, prichádzajú do úvahy 14 a 20. Im zodpovedajú počty cifier 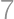 , resp.
, resp. 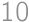 . Keďže sa striedajú párne a nepárne cifry, tak najmenšie čísla spĺňajúce všetko okrem deliteľnosti 7 sú 1010109 a 2101010109, ktoré majú ciferné súčty 12 a 15. Druhé číslo má nepárny ciferný súčet, a teda nevieme dosiahnúť súčet 20. V prvom prípade nám stačí zväčšiť ciferný súčet o 2, teda zväčšiť jednu z cifier o 2. Ľahko môžme zistiť, že jediná možnosť, kvôli deliteľnosti 7, je číslo 1010309.
. Keďže sa striedajú párne a nepárne cifry, tak najmenšie čísla spĺňajúce všetko okrem deliteľnosti 7 sú 1010109 a 2101010109, ktoré majú ciferné súčty 12 a 15. Druhé číslo má nepárny ciferný súčet, a teda nevieme dosiahnúť súčet 20. V prvom prípade nám stačí zväčšiť ciferný súčet o 2, teda zväčšiť jednu z cifier o 2. Ľahko môžme zistiť, že jediná možnosť, kvôli deliteľnosti 7, je číslo 1010309.
Úloha 52J / 42S
Štvorciferné číslo  je také, že posledné
je také, že posledné 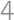 cifry z
cifry z 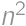 je číslo
je číslo  samo. Nájdite
samo. Nájdite  .
.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 53J / 43S
Zistite súčet všetkých päťciferných palindrómov. Palindróm je číslo, ktoré vyzerá rovnako spredu aj zozadu. Napr. 12321 je palindróm.
Zobrazit / skrýt výsledek
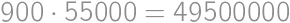 .
.
Úloha 54J / 44S
Majme štyri nepárne prirodzené čísla 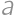 ,
, 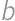 ,
, 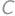 a
a 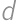 , ktoré spĺňajú
, ktoré spĺňajú 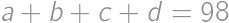 . Koľkými rôznymi spôsobmi môžeme tieto čísla vybrať?
. Koľkými rôznymi spôsobmi môžeme tieto čísla vybrať?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Najprv si úlohu zmeníme na jednoduchšiu tak, aby zostal výsledok rovnaký. Označíme si 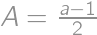 a rovnako označíme aj
a rovnako označíme aj 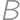 ,
, 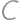 a
a 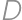 pre
pre 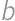 ,
, 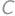 a
a 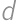 . Potom platí
. Potom platí 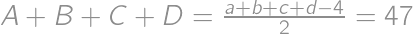 pre kladné celé
pre kladné celé 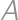 ,
, 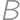 ,
, 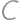 a
a 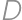 . Je vidno, že pre každú štvoricu
. Je vidno, že pre každú štvoricu 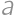 ,
, 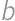 ,
, 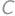 a
a 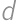 zo zadania existuje vyhovujúca štvorica
zo zadania existuje vyhovujúca štvorica 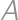 ,
, 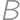 ,
, 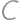 a
a 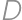 , a naopak. Toto už je štandardná úloha. Riešime ju tak, že si zoberieme 47 bielych guľôčok a 3 čierne. Rozostavíme ich do radu a čierne guľôčky rozdelia biele guľôčky na štyri úseky (potenciálne prázdne), ktoré označujú
, a naopak. Toto už je štandardná úloha. Riešime ju tak, že si zoberieme 47 bielych guľôčok a 3 čierne. Rozostavíme ich do radu a čierne guľôčky rozdelia biele guľôčky na štyri úseky (potenciálne prázdne), ktoré označujú 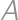 ,
,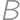 ,
,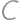 a
a 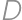 . Napríklad, ak sú čierne na pozíciách 5,6 a 25, tak úseky bielych sú 1-4, prázdny, 7-24 a 26-50 a
. Napríklad, ak sú čierne na pozíciách 5,6 a 25, tak úseky bielych sú 1-4, prázdny, 7-24 a 26-50 a 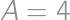 ,
, 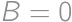 ,
, 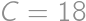 a
a 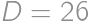 . Zase je vidno, že pre každé
. Zase je vidno, že pre každé 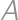 ,
,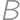 ,
,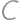 a
a 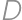 existuje práve jedna pozícia čiernych guľôčok, a naopak.Takže riešením je počet rozostavení 3 čiernych guľôčok na 50 pozíciách, ktorých je
existuje práve jedna pozícia čiernych guľôčok, a naopak.Takže riešením je počet rozostavení 3 čiernych guľôčok na 50 pozíciách, ktorých je 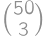 .
.
Úloha 55J / 45S
Nájdite jediné jedenásťciferné prirodzené číslo začínajúce jednotkou také, že keď ho napíšeme dvakrát za sebou, tak dostaneme druhú mocninu nejakého prirodzeného čísla.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 56J / 46S
Dva rôzne trojuholníky so stranami dĺžok 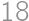 ,
,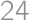 a
a 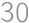 majú spoločnú vpísanú aj opísanú kružnicu. Aký obsah má ich spoločná plocha?
majú spoločnú vpísanú aj opísanú kružnicu. Aký obsah má ich spoločná plocha?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 57J / 47S
Majme mriežku 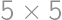 . Každý štvorček chceme zafarbiť bielou alebo čiernou farbou, aby platilo, že v každom riadku aj stĺpci sú práve dva čierne štvorčeky. Koľkými spôsobmi to vieme urobiť?
. Každý štvorček chceme zafarbiť bielou alebo čiernou farbou, aby platilo, že v každom riadku aj stĺpci sú práve dva čierne štvorčeky. Koľkými spôsobmi to vieme urobiť?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Úloha 58J / 48S
Body 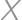 a
a 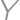 sú vo vnútri štvorca so stranou 1. Diaľkou vrchola štvorca označme jeho vzdialenosť k bližšiemu z bodov
sú vo vnútri štvorca so stranou 1. Diaľkou vrchola štvorca označme jeho vzdialenosť k bližšiemu z bodov 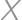 a
a 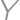 . Aký je najmenší možný súčet diaľok vrcholov štvorca?
. Aký je najmenší možný súčet diaľok vrcholov štvorca?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Prvý odhad získame, keď 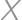 a
a 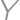 zvolíme ako rôzne vrcholy štvorca, potom je súčet diaľok 2. Pomocou trojuholníkových nerovností vieme zistiť, že ak je
zvolíme ako rôzne vrcholy štvorca, potom je súčet diaľok 2. Pomocou trojuholníkových nerovností vieme zistiť, že ak je  alebo
alebo  najbližšie k práve 0,2 alebo 4 vrcholom, tak súčet menší ako 2 nedosiahneme. Preto nech
najbližšie k práve 0,2 alebo 4 vrcholom, tak súčet menší ako 2 nedosiahneme. Preto nech  je bližšie k práve trom vrcholom (
je bližšie k práve trom vrcholom ( ,
, 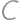 a
a 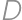 ) ako
) ako 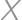 . Chceme minimalizovať
. Chceme minimalizovať 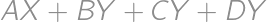 , ale
, ale 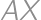 môže byť nula, ak
môže byť nula, ak 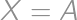 . Je známe, že súčet tých troch vzdialeností v trojuholníku
. Je známe, že súčet tých troch vzdialeností v trojuholníku 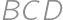 je najmenší, keď úsečky
je najmenší, keď úsečky 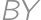 ,
,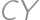 a
a 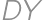 zvierajú 120 stupňov. (Túto skutočnosť môžeme overiť otočením trojuholníka
zvierajú 120 stupňov. (Túto skutočnosť môžeme overiť otočením trojuholníka 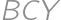 podľa bodu
podľa bodu 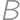 o
o 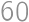 stupňov na
stupňov na 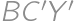 a minimalizáciou dĺžky lomenej čiary
a minimalizáciou dĺžky lomenej čiary 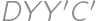 , čím bude úsečka
, čím bude úsečka 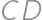 , ktorej dĺžku jednoducho vyjadríme.)
, ktorej dĺžku jednoducho vyjadríme.)
Úloha 59J / 49S
Parkovisko pozostáva z  parkovacích miest pravidelne rozložených v jednom rade označených číslami
parkovacích miest pravidelne rozložených v jednom rade označených číslami  až
až  . Postupne tam po jednom zaparkuje
. Postupne tam po jednom zaparkuje  áut, pričom postupujú nasledovne:
áut, pričom postupujú nasledovne:
- Prvé auto si náhodne vyberie jedno z 2012 miest.
- Každé ďalšie auto si vyberá s rovnakou pravdepodobnosťou zo všetkých miest, ktorých vzdialenosť od najbližšieho obsadeného miesta je v danej chvíli najväčšia.
Aká je pravdepodobnosť, že posledné auto zaparkuje na mieste s číslom
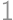 ?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
?
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Aby mohlo byť miesto číslo 1 obsadené ako posledné, musí byť miesto číslo 2 obsadené ako prvé (so šancou  ), a hneď po ňom sa obsadí pozícia
), a hneď po ňom sa obsadí pozícia  . Potom sa zaplnia niektoré miesta od
. Potom sa zaplnia niektoré miesta od 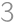 po
po 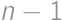 , až kým zostanú iba medzery veľkosti 1 a 2. V takom prípade je pravdepodobnosť, že 1. miesto bude obsadené ako posledné, rovná prevrátenej hodnote počtu voľných miest, keďže každé miesto má rovnakú šancu byť posledné. Uvedomíme si, že ak sa budeme pozerať iba na veľkosti medzier a postupne obsadzovať najväčšie, tak vždy nám zostane rovnaký počet medzier veľkosti 1 aj 2. A preto si vieme ich počet jednoznačne vypočítať. Nech
, až kým zostanú iba medzery veľkosti 1 a 2. V takom prípade je pravdepodobnosť, že 1. miesto bude obsadené ako posledné, rovná prevrátenej hodnote počtu voľných miest, keďže každé miesto má rovnakú šancu byť posledné. Uvedomíme si, že ak sa budeme pozerať iba na veľkosti medzier a postupne obsadzovať najväčšie, tak vždy nám zostane rovnaký počet medzier veľkosti 1 aj 2. A preto si vieme ich počet jednoznačne vypočítať. Nech 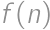 je počet miest, ktoré zostanú voľné, ak autá môžu parkovať na
je počet miest, ktoré zostanú voľné, ak autá môžu parkovať na 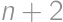 miestach za sebou, pričom prvé a posledné je obsadené. Prvé auto sa postaví do stredu a zostanú prípady
miestach za sebou, pričom prvé a posledné je obsadené. Prvé auto sa postaví do stredu a zostanú prípady 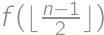 a
a 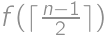 . A preto máme rekurentné vyjadrenie
. A preto máme rekurentné vyjadrenie 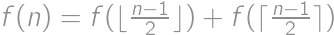 s bázou
s bázou 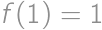 a
a 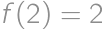 . Ak sa s tým pohráme a zrátame pre malé hodnoty, tak sa dostaneme k explicitnému vyjadreniu:
. Ak sa s tým pohráme a zrátame pre malé hodnoty, tak sa dostaneme k explicitnému vyjadreniu:
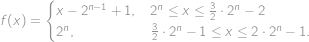
Preto
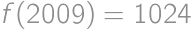
a celková pravdepodobnosť je
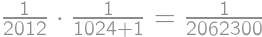 .
.
Úloha 60J / 50S
Nájdite všetky reálne čísla 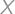 spĺňajúce
spĺňajúce 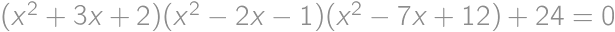 .
.
Zobrazit / skrýt výsledek
Zobrazit / skrýt řešení
Keďže
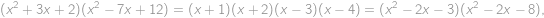
riešime po substitúcií
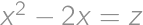
rovnicu
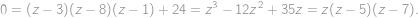
Pre každé
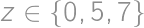
jednoducho zistíme zodpovedajúce
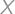 .
.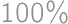 ,
,
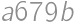 je päťciferné číslo deliteľné
je päťciferné číslo deliteľné 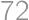 ,
,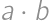 .
.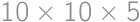 je na celom povrchu pokrytý tenkou vrstvou čokolády. Koláč rozrežeme na kocky
je na celom povrchu pokrytý tenkou vrstvou čokolády. Koláč rozrežeme na kocky 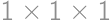 .
.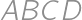 so stranou dĺžky
so stranou dĺžky 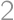 a bod
a bod 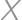 ležiaci mimo neho tak, že platí
ležiaci mimo neho tak, že platí 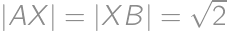 .
.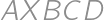 ?
?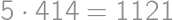 každú cifru zväčšite alebo zmenšite o 1 tak, aby bol výsledok správny. Aký bude výsledok?
každú cifru zväčšite alebo zmenšite o 1 tak, aby bol výsledok správny. Aký bude výsledok?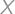 a
a 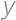 platí, že ich súčet je nanajvýš
platí, že ich súčet je nanajvýš 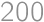 a ich rozdiel je menší ako
a ich rozdiel je menší ako 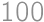 .
.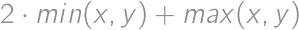 .
.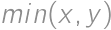 má hodnotu najmenšieho čísla z dvojice
má hodnotu najmenšieho čísla z dvojice 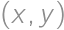 ,
,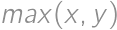 má hodnotu najväčšieho čísla z dvojice
má hodnotu najväčšieho čísla z dvojice 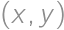 .
.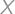 ,
,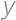 a
a 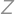 platí, že aritmetický priemer čísel
platí, že aritmetický priemer čísel 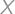 a
a 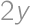 je rovný
je rovný 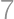 a aritmetický priemer čísel
a aritmetický priemer čísel 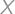 a
a 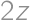 je rovný
je rovný 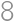 .
.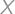 ,
,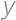 a
a 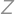 ?
?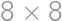 stojí 81 stromov. Záhradník vyrezal jeden z rohových stromov a teraz sa z jeho miesta pozerá na ostatné stromy. Niektoré však nevidí, pretože ich zakrývajú iné a to práve takto: strom
stojí 81 stromov. Záhradník vyrezal jeden z rohových stromov a teraz sa z jeho miesta pozerá na ostatné stromy. Niektoré však nevidí, pretože ich zakrývajú iné a to práve takto: strom 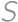 je zakrytý práve vtedy ak na úsečke medzi stromom
je zakrytý práve vtedy ak na úsečke medzi stromom 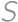 a záhradníkom leží iný strom, t.j. mrežový bod. Koľko stromov vidí záhradník?
a záhradníkom leží iný strom, t.j. mrežový bod. Koľko stromov vidí záhradník? 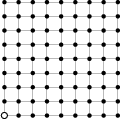
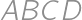 so stranami
so stranami 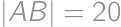 a
a 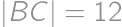 .
.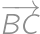 leží bod
leží bod 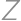 taký, že
taký, že 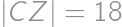 .
.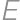 leží vo vnútri
leží vo vnútri 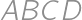 ,
,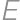 od
od 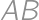 aj
aj 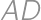 je
je 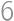 .
.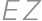 pretína strany
pretína strany 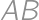 a
a 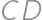 postupne v bodoch
postupne v bodoch 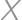 a
a 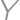 .
.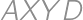 .
.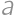 ,
, , je číslo
, je číslo 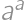 druhou mocninou prirodzeného čísla?
druhou mocninou prirodzeného čísla?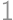 položený na podlahe. Jeden z jeho bodov zafarbíme na červeno. Trojuholník kotúľame po podlahe a trikrát ho preklopíme. Akú dlhú dráhu prejde červený bod?
položený na podlahe. Jeden z jeho bodov zafarbíme na červeno. Trojuholník kotúľame po podlahe a trikrát ho preklopíme. Akú dlhú dráhu prejde červený bod? ?
? rokmi bol jeho vek odmocninou z jeho veku o
rokmi bol jeho vek odmocninou z jeho veku o 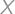 rokov. Billov vek je druhou mocninou prirodzeného čísla. Nájdite prirodzené číslo
rokov. Billov vek je druhou mocninou prirodzeného čísla. Nájdite prirodzené číslo 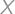 .
.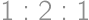 ?
?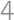 ?
?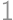 ,
,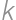 tak, aby sa jej zvnútra dotýkali všetky 3 kružnice. Vypočítajte polomer kružnice
tak, aby sa jej zvnútra dotýkali všetky 3 kružnice. Vypočítajte polomer kružnice 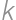 .
.
 je prirodzené číslo. Ak
je prirodzené číslo. Ak 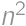 má cifru na mieste desiatok
má cifru na mieste desiatok 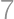 ,
,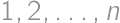 v nejakom poradí, získame tak
v nejakom poradí, získame tak  -reťazec.
-reťazec. -reťazcov
-reťazcov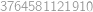
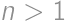 také, že existuje
také, že existuje  -reťazec,
-reťazec,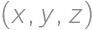 kladných reálnych čísel
kladných reálnych čísel 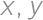 a
a 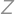 ,
,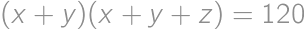 ,
,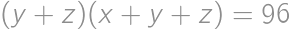 a
a 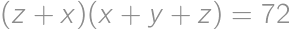 .
. a v ňom dve kolmé tetivy, ktoré delia kruh na
a v ňom dve kolmé tetivy, ktoré delia kruh na  časti. Ofarbíme časť s najväčším a časť s najmenším obsahom čiernou, zvyšné necháme biele. Vieme, že obsah bielych častí bude taký ako obsah čiernych častí. Aká je maximálna možná vzdialenosť dlhšej tetivy od stredu kružnice?
časti. Ofarbíme časť s najväčším a časť s najmenším obsahom čiernou, zvyšné necháme biele. Vieme, že obsah bielych častí bude taký ako obsah čiernych častí. Aká je maximálna možná vzdialenosť dlhšej tetivy od stredu kružnice? ,
,
 ,
,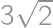 ,
, 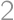 a
a 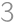 v tomto poradí, pričom rovnobežné sú strany dlhé
v tomto poradí, pričom rovnobežné sú strany dlhé 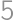 a
a 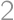 .
.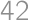 ľudí a chcú sa zoradiť podľa výšky tak, aby vpredu stál najvyšší. V jednom ťahu si môžu vymeniť miesto dvaja za sebou. Koľko najmenej ťahov potrebujú na to, aby sa týmto spôsobom zoradili, keď stoja na začiatku ľubovoľne?
ľudí a chcú sa zoradiť podľa výšky tak, aby vpredu stál najvyšší. V jednom ťahu si môžu vymeniť miesto dvaja za sebou. Koľko najmenej ťahov potrebujú na to, aby sa týmto spôsobom zoradili, keď stoja na začiatku ľubovoľne?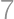 alebo
alebo 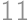 .
.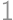 ľubovoľným spôsobom na štyri súvislé časti. Aký najmenší obvod môže mať časť s najväčším obsahom? Ak má viacero častí najväčší obsah, tak berieme tú s najmenším obvodom.
ľubovoľným spôsobom na štyri súvislé časti. Aký najmenší obvod môže mať časť s najväčším obsahom? Ak má viacero častí najväčší obsah, tak berieme tú s najmenším obvodom.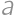 ,
,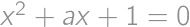 a
a 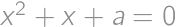 aspoň jeden spoločný reálny koreň.
aspoň jeden spoločný reálny koreň. -krát
-krát ,
, je trojuholník so stredom kružnice opísanej
je trojuholník so stredom kružnice opísanej  a priesečníkom výšok
a priesečníkom výšok  ,
, ,
, ,
,  ,
, a
a  majú celočíselné súradnice a žiadne dva nesplývajú. Aký je druhý najmenší možný polomer kružnice opísanej trojuholníku
majú celočíselné súradnice a žiadne dva nesplývajú. Aký je druhý najmenší možný polomer kružnice opísanej trojuholníku  ?
? také, že číslo
také, že číslo 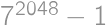 je deliteľné
je deliteľné 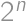 .
.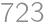 má vytrvalosť
má vytrvalosť 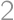 ,
,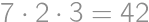 (1. krok) a
(1. krok) a 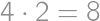 (2. krok). Nájdite najväčšie párne číslo s navzájom rôznymi nenulovými ciframi a vytrvalosťou
(2. krok). Nájdite najväčšie párne číslo s navzájom rôznymi nenulovými ciframi a vytrvalosťou 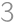 .
.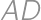 a
a 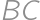 konvexného štvoruholníka
konvexného štvoruholníka 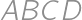 predĺžime, tak sa pretnú v bode
predĺžime, tak sa pretnú v bode 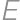 .
. a
a 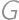 postupne stredy
postupne stredy 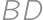 a
a 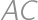 .
.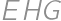 a obsahu štvoruholníka
a obsahu štvoruholníka 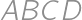 .
.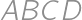 ,
,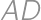 a
a 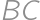 nie sú rovnobežné.
nie sú rovnobežné. v každom smere štyri rovné chodbičky ako na obrázku a opustili ju. To, čo z kocky zostalo, chceme ofarbiť antitermitovou farbou. Koľko centimetrov štvorcových musíme ofarbiť?
v každom smere štyri rovné chodbičky ako na obrázku a opustili ju. To, čo z kocky zostalo, chceme ofarbiť antitermitovou farbou. Koľko centimetrov štvorcových musíme ofarbiť? 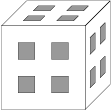
 a stojíme na najľavejšom bode jeho obvodu. Môžeme sa hýbať len doprava a hore. Akú dĺžku má najdlhšia trasa, ktorú môžeme prejsť, ak nechceme z kruhu vyjsť?
a stojíme na najľavejšom bode jeho obvodu. Môžeme sa hýbať len doprava a hore. Akú dĺžku má najdlhšia trasa, ktorú môžeme prejsť, ak nechceme z kruhu vyjsť?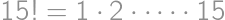 taký, že po vydelení
taký, že po vydelení 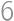 dáva zvyšok
dáva zvyšok 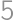 ?
?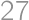 bodov: vrcholy kocky, stredy hrán, stredy stien a stred kocky. Koľko je priamok, ktoré prechádzajú práve cez tri body?
bodov: vrcholy kocky, stredy hrán, stredy stien a stred kocky. Koľko je priamok, ktoré prechádzajú práve cez tri body?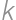 dní sa zúčastnilo
dní sa zúčastnilo  účastníkov. Každý deň všetci účastníci získali skóre
účastníkov. Každý deň všetci účastníci získali skóre 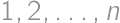 bodov, pričom žiadni dvaja nemali rovnaký počet bodov za daný deň. Na konci súťaže (
bodov, pričom žiadni dvaja nemali rovnaký počet bodov za daný deň. Na konci súťaže (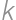 -ty deň večer po súťaži) mal každý účastník v súčte za všetky dni skóre
-ty deň večer po súťaži) mal každý účastník v súčte za všetky dni skóre 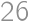 bodov. Nezávisle od
bodov. Nezávisle od 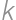 ,
, ,
, .
. minútach stretne auto je
minútach stretne auto je 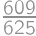 .
.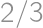 šancu na nájdenie každej jednotlivej chyby, ktorá ešte v článku je. Aká je šanca, že po troch dňoch bude článok bezchybný?
šancu na nájdenie každej jednotlivej chyby, ktorá ešte v článku je. Aká je šanca, že po troch dňoch bude článok bezchybný?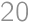 -stennú
-stennú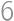 -stenné
-stenné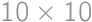 .
. po
po 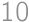 .
.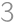 ,
,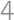 a
a 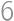 .
.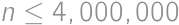 ,
,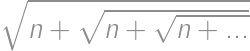 racionálny.
racionálny.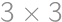 tvorený deviatimi štvorcovými kachličkami. Každá kachlička je rozdelená na štyri rovnaké štvorčeky, v ktorých sú vpísané čísla
tvorený deviatimi štvorcovými kachličkami. Každá kachlička je rozdelená na štyri rovnaké štvorčeky, v ktorých sú vpísané čísla 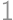 ,
,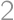 ,
, 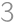 a
a 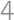 (každé práve raz). Dve kachličky sa môžu dotýkať len rovnakými číslami (ako dominá). Koľko rôznych Maxištvorcov existuje?
(každé práve raz). Dve kachličky sa môžu dotýkať len rovnakými číslami (ako dominá). Koľko rôznych Maxištvorcov existuje? 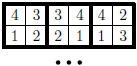
 je také, že posledné
je také, že posledné 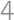 cifry z
cifry z 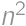 je číslo
je číslo  samo. Nájdite
samo. Nájdite  .
.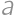 ,
,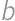 ,
, 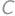 a
a 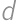 ,
,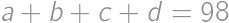 .
.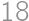 ,
,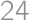
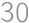 majú spoločnú vpísanú aj opísanú kružnicu. Aký obsah má ich spoločná plocha?
majú spoločnú vpísanú aj opísanú kružnicu. Aký obsah má ich spoločná plocha?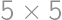 .
.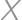 a
a  sú vo vnútri štvorca so stranou 1. Diaľkou vrchola štvorca označme jeho vzdialenosť k bližšiemu z bodov
sú vo vnútri štvorca so stranou 1. Diaľkou vrchola štvorca označme jeho vzdialenosť k bližšiemu z bodov  a
a  .
.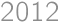 parkovacích miest pravidelne rozložených v jednom rade označených číslami
parkovacích miest pravidelne rozložených v jednom rade označených číslami  až
až 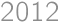 .
.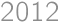 áut, pričom postupujú nasledovne:
áut, pričom postupujú nasledovne:  ?
?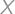 spĺňajúce
spĺňajúce  .
.
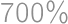
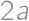 .
.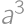 ,
,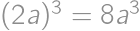 .
.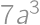 ,
,
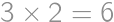
 (
(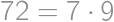 ). Z kritéria deliteľnosti 8 máme, že
). Z kritéria deliteľnosti 8 máme, že  ,
,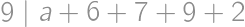 ,
, .
.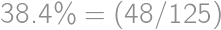
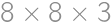 zložený zo všetkých kúskov bez čokolády, takže ich musí byť 192. Z celkového počtu
zložený zo všetkých kúskov bez čokolády, takže ich musí byť 192. Z celkového počtu 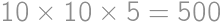 kúskov už ľahko zrátame percentá:
kúskov už ľahko zrátame percentá: 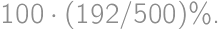
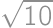
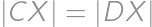 .
.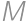 je stred strany
je stred strany 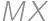 .
.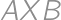 je pravouhlý rovnoramenný (z Pytagorovej vety), takže
je pravouhlý rovnoramenný (z Pytagorovej vety), takže 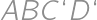 (
(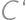 a
a 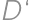 získame preklopením
získame preklopením 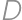 cez
cez 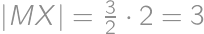 .
.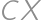 už zrátame jednoducho z Pytagorovej vety:
už zrátame jednoducho z Pytagorovej vety: 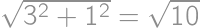 .
.
 .
.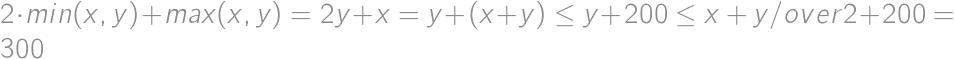 .
.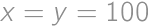 .
.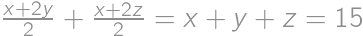 .
.
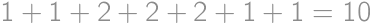
 ,
,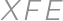 a
a 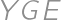 sú zhodné, takže obsah
sú zhodné, takže obsah 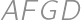 ,
,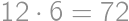 .
.
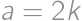 je číslo
je číslo 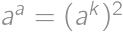 určite druhou mocninou. Pre nepárne čísla
určite druhou mocninou. Pre nepárne čísla 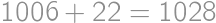 .
.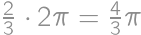
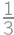 z obvodu kružnice a raz zostane na mieste. Dokopy prejde dráhu dĺžky
z obvodu kružnice a raz zostane na mieste. Dokopy prejde dráhu dĺžky 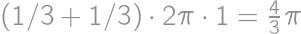 .
.
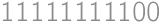
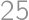 (lebo
(lebo 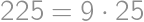 ).
).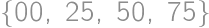 .
.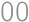 .
.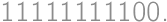
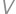 ,
,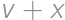 je taktiež druhou mocninou. Stačí vyskúšať niekoľko možností.
je taktiež druhou mocninou. Stačí vyskúšať niekoľko možností.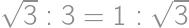 pripadne v opacnom poradi.
pripadne v opacnom poradi.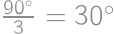 .
.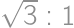 .
.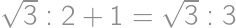
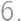 Rovnako je číslo deliteľné aj tromi, a preto jeho ciferný súčet je deliteľný tromi, čiže súčet prvých dvoch cifier musí dávať po delení 3 zvyšok
Rovnako je číslo deliteľné aj tromi, a preto jeho ciferný súčet je deliteľný tromi, čiže súčet prvých dvoch cifier musí dávať po delení 3 zvyšok 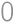 (ak je posledná
(ak je posledná 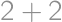 ,
,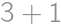 (záleží aj na poradí cifier, takže máme
(záleží aj na poradí cifier, takže máme 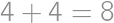 možností.). Podobne zvyšok
možností.). Podobne zvyšok 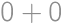 ,
,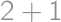 (znovu máme
(znovu máme 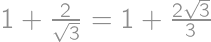
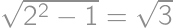 .
.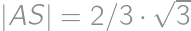 .
.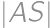 .
.
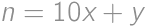 ,
,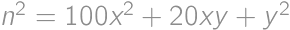 .
.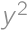 .
.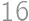 alebo
alebo 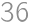 .
.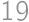 -reťazcom:
-reťazcom: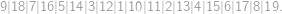
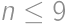 ,
,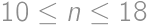 sa cifry
sa cifry 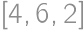
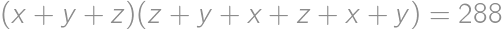 .
. ,
,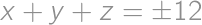 ,
,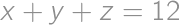 .
.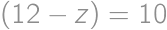 ,
,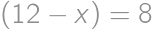 ,
, 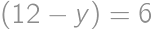 ,
,
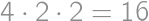 možných ciest.
možných ciest.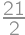
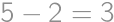 ,
, 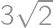 ,
,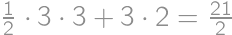 .
.
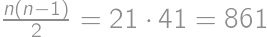
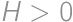 ,
,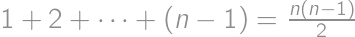 ,
,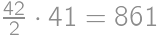 ťahov.
ťahov. dáva
dáva 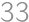 dáva
dáva 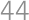 dáva
dáva 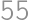 dáva
dáva 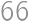 dáva zvyšok
dáva zvyšok 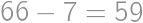 .
.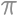
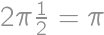 .
.
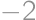
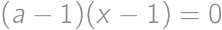 .
.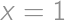 alebo
alebo  .
.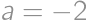 .
.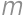 je číslo, ktoré nám zostane po škrtnutí prvej cifry. Pôvodné číslo potom musí vyzerať
je číslo, ktoré nám zostane po škrtnutí prvej cifry. Pôvodné číslo potom musí vyzerať 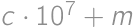 ,
,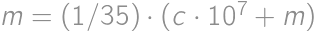 ,
,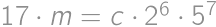 .
. ,
,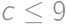 .
.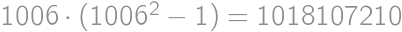
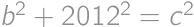 .
.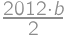 ,
,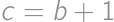 ,
,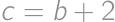 do Pytagorovej vety dostaneme jednoduchú rovnicu pre
do Pytagorovej vety dostaneme jednoduchú rovnicu pre 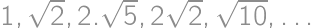 . Pre polomery
. Pre polomery 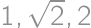 a
a 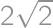 vidíme, že vždy je jeden z vrcholov trojuholníka priesečníkom výšok. Pre
vidíme, že vždy je jeden z vrcholov trojuholníka priesečníkom výšok. Pre 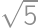 a
a 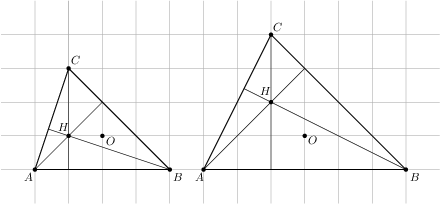
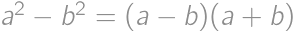 dostávame:
dostávame: 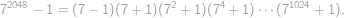
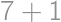 deliteľný 2 práve raz, čo sa dá jednoducho overiť skúmaním zvyškov
deliteľný 2 práve raz, čo sa dá jednoducho overiť skúmaním zvyškov 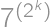 po delení 4.
po delení 4.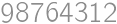
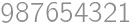 ,
,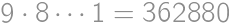 ,
,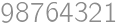 je 3, lebo
je 3, lebo 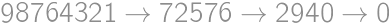 .
.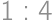
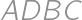 je rovnoramenný lichobežník so stranami 1, 1, 1 a
je rovnoramenný lichobežník so stranami 1, 1, 1 a 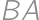 = 2, to vychádza ľahko aj bez väčšieho počítania, keďže je tam veľa rovnostranných trojuholníkov. V riešení pre všeobecný prípad budeme
= 2, to vychádza ľahko aj bez väčšieho počítania, keďže je tam veľa rovnostranných trojuholníkov. V riešení pre všeobecný prípad budeme 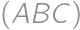 označovať obsah
označovať obsah 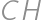 ,
,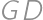 ,
, 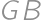 .
.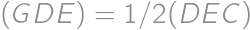 .
.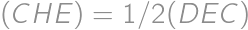 .
.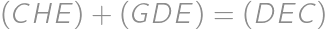 .
.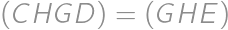 .
.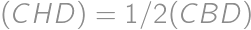 a
a 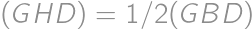 ,
,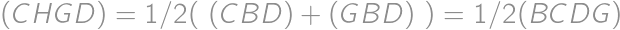 .
.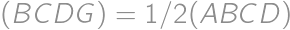 ,
,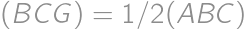 a
a 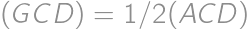 .
.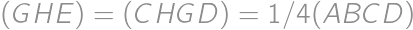 .
.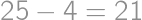 .
.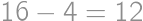 .
.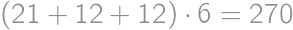 plôšok.
plôšok.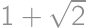
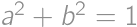 a chceme maximalizovať
a chceme maximalizovať  .
.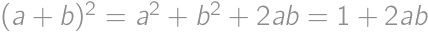 . Z triviálnej nerovnosti
. Z triviálnej nerovnosti 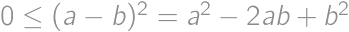 máme
máme 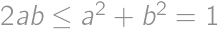 .
.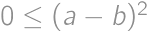 ,
,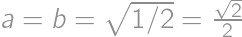 .
.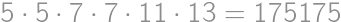
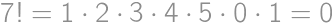 .
.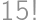 musíme vyhodiť všetky dvojky a trojky. Zostane nám číslo
musíme vyhodiť všetky dvojky a trojky. Zostane nám číslo 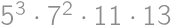 a dáva zvyšok 1. Keďže
a dáva zvyšok 1. Keďže 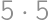 dáva zvyšok 1, tak nám stačí vyhodiť jedno číslo so zvyškom 5 a najmenším takým je samozrejme 5.
dáva zvyšok 1, tak nám stačí vyhodiť jedno číslo so zvyškom 5 a najmenším takým je samozrejme 5.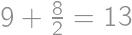 .
.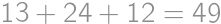 priamok.
priamok.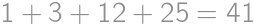
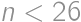 .
.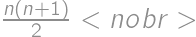 bodov, čo dáva celkový súčet
bodov, čo dáva celkový súčet 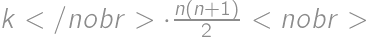 bodov. To je ale tiež rovné
bodov. To je ale tiež rovné 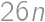 . Z toho dostávame
. Z toho dostávame 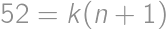 .
.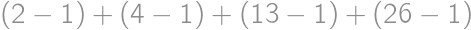 .
.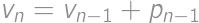 kde
kde 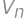 je výsledok pre
je výsledok pre 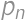 je počet nových častí = počet oblastí, na ktoré vieme rozdeliť rovinu
je počet nových častí = počet oblastí, na ktoré vieme rozdeliť rovinu 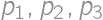 a
a 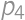 ako
ako 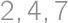 a
a 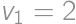 ,
,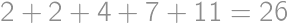 .
.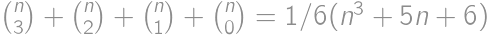 .
.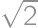
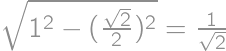 ,
,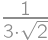 .
.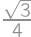 a výšku
a výšku 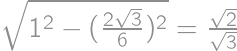 ,
,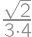 .
.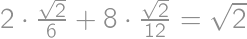 .
.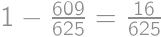 .
.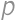 ,
,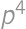 .
.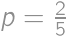 .
.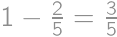 .
.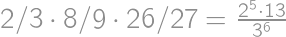
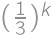 a pravdepodobnosť, že nejaká chyba nevydrží
a pravdepodobnosť, že nejaká chyba nevydrží 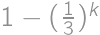 .
.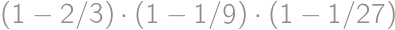 .
.
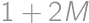 (jeden bod za seba a dva za každú modrú kartu) a každá žltá karta prispieva
(jeden bod za seba a dva za každú modrú kartu) a každá žltá karta prispieva 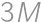 .
. ,
,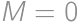 ,
,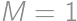 ,
,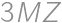 ,
,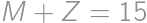 .
.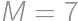 a
a 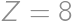 ,
,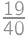
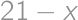 (od 1 po 20). A podobne pravdepodobnosť, že padne
(od 1 po 20). A podobne pravdepodobnosť, že padne 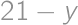 (od 3 po 18). Podobnou úvahou zistíme, že pravdepodobnosť výhry Matúša je rovnaká, ako pravdepodobnosť výhry CDčka. Preto je výsledok
(od 3 po 18). Podobnou úvahou zistíme, že pravdepodobnosť výhry Matúša je rovnaká, ako pravdepodobnosť výhry CDčka. Preto je výsledok 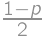 kde
kde 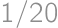 ,
,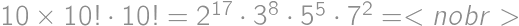
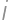 okrem
okrem  budú vo výslednom súčine práve dvakrát. Keďže v pravom dolnom rohu (
budú vo výslednom súčine práve dvakrát. Keďže v pravom dolnom rohu (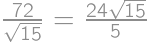
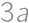 a
a 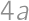 ,
,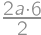 .
.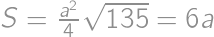 z čoho dostaneme
z čoho dostaneme 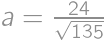 a obvod je
a obvod je 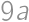 .
.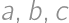 je
je 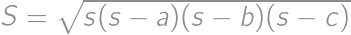 ,
,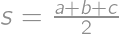 a
a 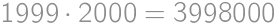
 .
.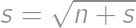 .
.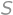 je
je 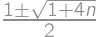 ,
,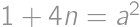 ,
,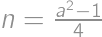 .
.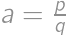 je vykrátený zlomok, tak
je vykrátený zlomok, tak 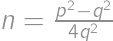 má byť celé číslo, a teda
má byť celé číslo, a teda 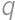 by muselo deliť
by muselo deliť 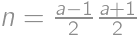 ,
,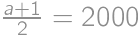 ,
,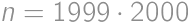 .
.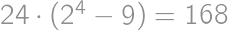
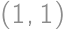 ,
,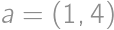 ,
,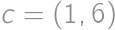 ,
, 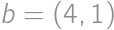 a
a 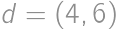 .
.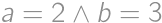 kvôli strednej kachličke,
kvôli strednej kachličke, 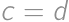 kvôli pravej dolnej,
kvôli pravej dolnej,  kvôli pravej strednej a
kvôli pravej strednej a 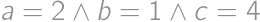 kvôli strednej dolnej. To nám dokopy vylúči 9 možností (jednu sme zarátali dvakrát). Nezabudnime výsledok vynásobiť 24 — toľko je možností ako môže vyzerať prvá kachlička.
kvôli strednej dolnej. To nám dokopy vylúči 9 možností (jednu sme zarátali dvakrát). Nezabudnime výsledok vynásobiť 24 — toľko je možností ako môže vyzerať prvá kachlička.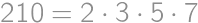 .
.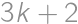 .
.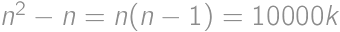 pre nejaké prirodzené
pre nejaké prirodzené 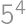 delí pravú stranu, a preto
delí pravú stranu, a preto 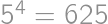 delí buď
delí buď 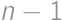 .
.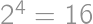 delí buď
delí buď 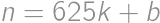 kde
kde 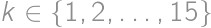 a
a 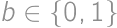 .
.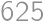 dáva zvyšok 1 po delení 16, tak
dáva zvyšok 1 po delení 16, tak 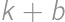 po delení 16. Z druhej deliteľnosti musí byť teda
po delení 16. Z druhej deliteľnosti musí byť teda 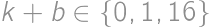 a štvorciferný výsledok dostaneme jedine pre
a štvorciferný výsledok dostaneme jedine pre 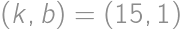 ,
,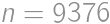 .
.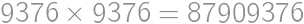 ,
,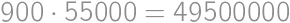 .
.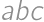 vieme priradiť palindróm
vieme priradiť palindróm 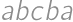 pre
pre 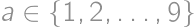 a
a 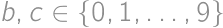 .
.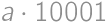 ,
,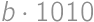 a každé
a každé 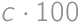 k celkovému súčtu. Každá z možností pre
k celkovému súčtu. Každá z možností pre 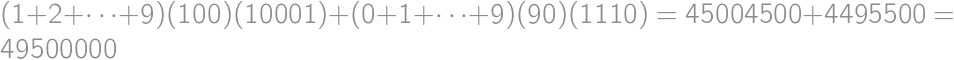 .
.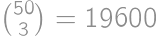
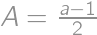 a rovnako označíme aj
a rovnako označíme aj 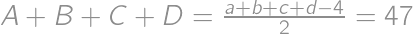 pre kladné celé
pre kladné celé 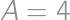 ,
,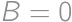 ,
, 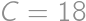 a
a 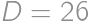 .
.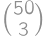 .
.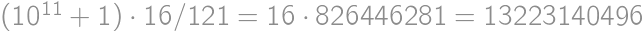
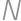 vzniknuté zapísaním pôvodného čísla
vzniknuté zapísaním pôvodného čísla 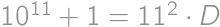 .
.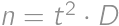 ,
,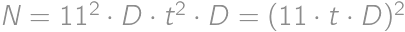 .
.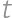 tak, aby
tak, aby 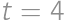 a zo zadania vieme, že je jediné také.
a zo zadania vieme, že je jediné také.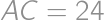 ,
, 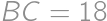 ).
).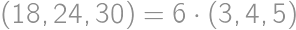 ,
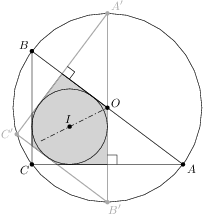
,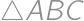 je pravouhlý a pre polomery vpísanej a opísanej kružnice platí
je pravouhlý a pre polomery vpísanej a opísanej kružnice platí 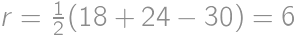 a
a 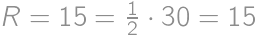 .
.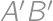 opísanej kružnice rôzny od
opísanej kružnice rôzny od 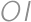 .
.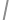 vzdialenosť 6. Druhý trojuholník
vzdialenosť 6. Druhý trojuholník 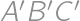 bude preto symetrický s
bude preto symetrický s 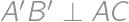 a
a 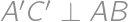 .
.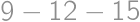 (u
(u 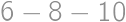 (u
(u 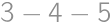 (u
(u 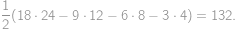
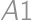 až
až 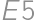 (čísla sú riadky). Postupne ofarbíme desať políčok načierno. Bez ujmy na všeobecnosti (bunv), nech sú ofarbené
(čísla sú riadky). Postupne ofarbíme desať políčok načierno. Bez ujmy na všeobecnosti (bunv), nech sú ofarbené 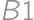 (výsledok potom stačí zo symetrie vynásobiť
(výsledok potom stačí zo symetrie vynásobiť 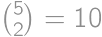 )
)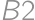 (a štyrmi). Ďalej, ak je v druhom riadku ofarbené políčko
(a štyrmi). Ďalej, ak je v druhom riadku ofarbené políčko 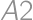 ,
,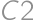 (násobíme troma) a v treťom stĺpci ešte
(násobíme troma) a v treťom stĺpci ešte 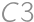 (opäť troma). Ak je ofarbené políčko
(opäť troma). Ak je ofarbené políčko  ,
,
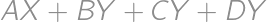 ,
,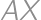 môže byť nula, ak
môže byť nula, ak 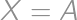 .
.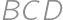 je najmenší, keď úsečky
je najmenší, keď úsečky 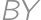 ,
,
 zvierajú 120 stupňov. (Túto skutočnosť môžeme overiť otočením trojuholníka
zvierajú 120 stupňov. (Túto skutočnosť môžeme overiť otočením trojuholníka  podľa bodu
podľa bodu  stupňov na
stupňov na 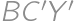 a minimalizáciou dĺžky lomenej čiary
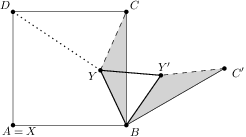
a minimalizáciou dĺžky lomenej čiary 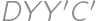 ,
,
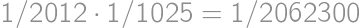
 ),
),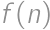 je počet miest, ktoré zostanú voľné, ak autá môžu parkovať na
je počet miest, ktoré zostanú voľné, ak autá môžu parkovať na 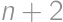 miestach za sebou, pričom prvé a posledné je obsadené. Prvé auto sa postaví do stredu a zostanú prípady
miestach za sebou, pričom prvé a posledné je obsadené. Prvé auto sa postaví do stredu a zostanú prípady 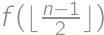 a
a 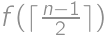 .
.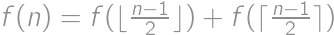 s bázou
s bázou 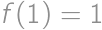 a
a 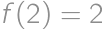 .
.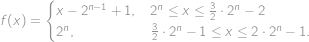
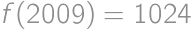 a celková pravdepodobnosť je
a celková pravdepodobnosť je 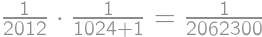 .
.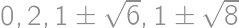
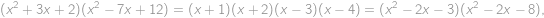
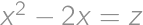 rovnicu
rovnicu 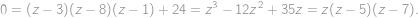
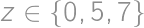 jednoducho zistíme zodpovedajúce
jednoducho zistíme zodpovedajúce 




















