Ülesanne 1
Čitateľ aj menovateľ Jefovho zlomku sú prirodzené čísla so súčtom 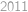 . Hodnota zlomku je pritom menšia ako
. Hodnota zlomku je pritom menšia ako 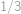 . Aká najväčšia môže byť hodnota Jefovho zlomku?
. Aká najväčšia môže byť hodnota Jefovho zlomku?
Peida / näita vastust
 .
.
Hledáme vlastně největší přirozené číslo 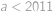 splňující nerovnici
splňující nerovnici
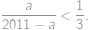
Tu ekvivalentně upravíme do tvaru
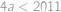
a vidíme, že největší vyhovující

je
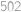
a výsledný zlomek je pak roven
 .
.
Ülesanne 2
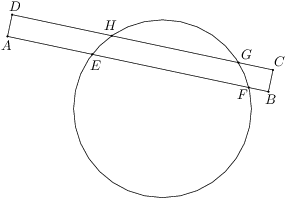
Na obrázku pretína obdĺžnik 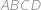 kružnicu v bodoch
kružnicu v bodoch 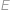 ,
, 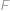 ,
, 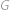 ,
, 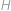 . Vieme, že
. Vieme, že 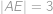 ,
, 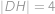 a
a 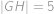 . Vypočítajte dĺžku úsesčky
. Vypočítajte dĺžku úsesčky 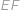 .
.
Peida / näita vastust
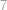 .
.
Označme
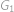 ,
, 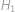
po řadě průměty bodů
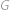 ,
, 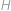
na přímku
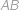 .
. Potom zřejmě
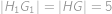 .
. Dále si všimneme, že díky osové souměrnosti je
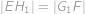
a navíc
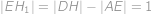 .
. Tedy
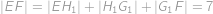 .
.
Ülesanne 3
Vypočítajte ciferný súčet čísla 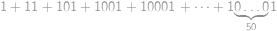 .
.
Peida / näita vastust
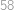 .
.
Upravujme
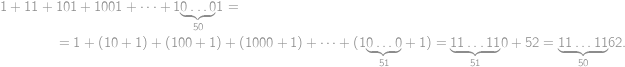
Hledaný ciferný součet je tedy roven
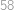 .
.
Ülesanne 4
Niekoľko mandaríniek sme rozdelili do troch sáčkov. V prvom sáčku je o šesť mandaríniek menej ako v zvyšných dvoch sáčkoch dohromady. Podobne, v druhom sáčku je o 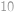 mandaríniek menej ako v zvyšných dvoch sáčkoch dohromady. Koľko mandaríniek je v treťom sáčku?
mandaríniek menej ako v zvyšných dvoch sáčkoch dohromady. Koľko mandaríniek je v treťom sáčku?
Peida / näita vastust
 .
.
Označme  ,
, 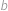 ,
,  postupně počty mandarinek v prvním, druhém a třetím sáčku. Podle zadání je
postupně počty mandarinek v prvním, druhém a třetím sáčku. Podle zadání je
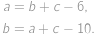
Po sečtení rovnic můžeme od obou stran odečíst
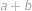
a dopočteme
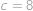 .
.
Ülesanne 5
Na stole je 33 orechov rozdelených aspoň na dve kôpky. V každej kôpke sú aspoň dva orechy. Ak zo všetkých kôpok zoberieme jeden orech a položíme ho na prvú kôpku, tak bude na všetkých kôpkach rovnako veľa orechov. Koľko kôpok mohlo byť pôvodne na stole? Zistite všetky možnosti.
Peida / näita vastust
 .
.
Ülesanne 6
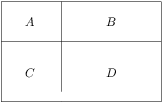
Obdĺžnik je dvoma úsečkami rovnobežnými s jeho stranami rozdelený na štyri menšie obdĺžniky. Označme ich  ,
,  ,
, 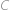 ,
,  rovnako ako na obrázku. Obvody obdĺžnikov
rovnako ako na obrázku. Obvody obdĺžnikov  ,
,  a
a 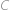 sú po rade
sú po rade  cm,
cm,  cm a
cm a 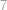 cm. Aké hodnoty môže nadobúdať obvod obdĺžnika
cm. Aké hodnoty môže nadobúdať obvod obdĺžnika  ?
?
Peida / näita vastust
 cm.
cm.
Označme délky
 ,
, 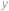
,
 ,
, 
jako na obrázku. Pro obvody obdélníků
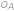 ,
, 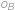
,
 ,
, 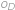
pak platí
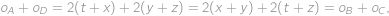
takže
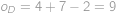
cm.
Ülesanne 7
Nájdite rozdielne cifry  ,
,  a
a 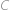 (v desiatkovej sústave) také, aby platil nasledujúci sčítací vzťah:
(v desiatkovej sústave) také, aby platil nasledujúci sčítací vzťah:
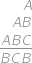
Peida / näita vastust
Peida / näita lahendust
Ülesanne 8
Určte obsah obdĺžnika, ak viete, že jeho obvod je 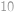 cm a jeho uhlopriečka má dĺžku
cm a jeho uhlopriečka má dĺžku 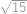 cm.
cm.
Peida / näita vastust
 cm
cm .
.
Ülesanne 9
Edo si zobral 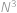 rovnako veľkých kociek a postavil z nich jednu veľkú kocku o rozmeroch
rovnako veľkých kociek a postavil z nich jednu veľkú kocku o rozmeroch 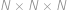 . Celý povrch veľkej kocky zafarbil a potom ju celú rozložil na pôvodné kocky. Určte
. Celý povrch veľkej kocky zafarbil a potom ju celú rozložil na pôvodné kocky. Určte 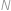 , ak viete, že je zafarbená desatina celkového povrchu malých kociek.
, ak viete, že je zafarbená desatina celkového povrchu malých kociek.
Peida / näita vastust
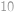 .
.
Ülesanne 10
Koľko najmenej členov má matematický klub, v ktorom je zastúpenie žien väčšie ako 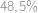 , ale menšie ako
, ale menšie ako 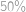 ?
?
Peida / näita vastust
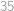 .
.
Ülesanne 11
Ak zväčšíte číslo úlohy, ktorú práve držíte v ruke o číslo  , získate číslo úlohy s najviac šokujúcim zadaním. Ak ho ale zväčšíte o dvojciferné číslo
, získate číslo úlohy s najviac šokujúcim zadaním. Ak ho ale zväčšíte o dvojciferné číslo 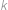 , získate číslo najhravejšej úlohy. Naviac platí, že
, získate číslo najhravejšej úlohy. Naviac platí, že 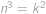 . Určte
. Určte  a
a 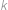 , ak viete, že vám zostáva ešte
, ak viete, že vám zostáva ešte 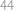 úloh (vrátane tejto).
úloh (vrátane tejto).
Peida / näita vastust
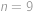 ,
, 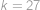 .
.
Ülesanne 12
Nájdite prirodzené číslo  spĺňajúce vzťah
spĺňajúce vzťah 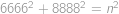 .
.
Peida / näita vastust
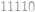 .
.
Počítání si usnadníme vytýkáním, tedy
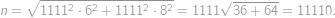
Ülesanne 13
Nájdite najmenšie prirodzené číslo, ktorého desiatkový zápis končí na 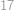 , je deliteľné
, je deliteľné 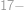 timi a má ciferný súčet
timi a má ciferný súčet 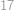 .
.
Peida / näita vastust
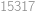 .
.
Ülesanne 14
Každá dvojica po sebe idúcich cifier istého 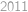 -ciferného čísla je násobkom
-ciferného čísla je násobkom 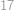 alebo
alebo 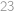 . Jeho posledná cifra je
. Jeho posledná cifra je 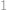 . Určte jeho prvú cifru.
. Určte jeho prvú cifru.
Peida / näita vastust
 .
.
Ülesanne 15
Prirodzené číslo nazveme luxusné, ak každé iné číslo s rovnakým ciferným súčtom je od neho väčšie. Zistite, koľko je trojciferných luxusných čísel.
Peida / näita vastust
 .
.
Ülesanne 16
Škrečkove reálne čísla  ,
, 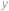 ,
,  spĺňajú
spĺňajú 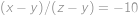 . Aké hodnoty môže nadobúdať výraz
. Aké hodnoty môže nadobúdať výraz 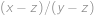 ? Nájdite všetky možnosti.
? Nájdite všetky možnosti.
Peida / näita vastust
 .
.
Ülesanne 17
Číslice 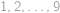 napíšeme za sebou v nejakom poradí tak, aby vzniklo deväťciferné číslo. Uvažujme všetky trojice po sebe idúcich cifier tohto čísla a k týmto trojiciam zodpovedajúce trojciferné čísla sčítame. Aký najväčší výsledok môžeme dostať?
napíšeme za sebou v nejakom poradí tak, aby vzniklo deväťciferné číslo. Uvažujme všetky trojice po sebe idúcich cifier tohto čísla a k týmto trojiciam zodpovedajúce trojciferné čísla sčítame. Aký najväčší výsledok môžeme dostať?
Peida / näita vastust
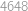 .
.
Označíme cifry 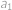 ,
, 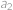 , … ,
, … , 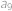 . Jednotlivé trojice jsou pak rovny:
. Jednotlivé trojice jsou pak rovny:
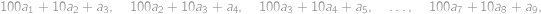
takže jejich součet je roven
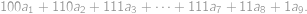
Chceme-li tento součet maximalizovat, použijeme nejvyšší čísla pro cifry
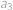
až
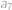 .
. Dále
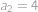 ,
, 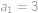
,
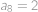 ,
, 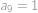
. Součet vyjde
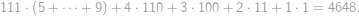
Ülesanne 18
V každom políčku tabuľky 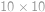 je napísané číslo. Filip si vybral dve čísla z tabuľky a do zošita si napísal ich súčin. Toto spravil pre všetky dvojice čísel z tabuľky. Všimol si, že práve
je napísané číslo. Filip si vybral dve čísla z tabuľky a do zošita si napísal ich súčin. Toto spravil pre všetky dvojice čísel z tabuľky. Všimol si, že práve 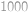 z týchto súčinov je záporných. Koľko z pôvodných čísel mohlo byť rovných nule? Vypíšte všetky možnosti.
z týchto súčinov je záporných. Koľko z pôvodných čísel mohlo byť rovných nule? Vypíšte všetky možnosti.
Peida / näita vastust
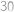 ,
, 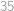 .
.
Ülesanne 19
V istom kráľovstve začali raziť mince. Počas prvého dňa razili mince v hodnote 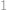 fufeň. Každý ďalší deň razili mince v najmenšej hodnote, ktorá sa nedala zaplatiť pomocou maximálne desiatich už vyrazených mincí. Mince akej hodnoty razili počas
fufeň. Každý ďalší deň razili mince v najmenšej hodnote, ktorá sa nedala zaplatiť pomocou maximálne desiatich už vyrazených mincí. Mince akej hodnoty razili počas 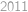 -teho dňa?
-teho dňa?
Peida / näita vastust
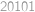 (fufníků).
(fufníků).
Ülesanne 20
Označme 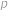 riešenie úlohy na tomto papieri. Určte pravdepodobnosť (číslo z intervalu
riešenie úlohy na tomto papieri. Určte pravdepodobnosť (číslo z intervalu 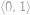 ), že náhodne vybraný bod vnútri štvorca so stranou
), že náhodne vybraný bod vnútri štvorca so stranou 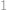 cm je od všetkých jeho strán vzdialený aspoň
cm je od všetkých jeho strán vzdialený aspoň 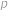 cm.
cm.
Peida / näita vastust
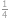 .
.
Bod je od každé strany vzdálený alespoň 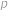 cm právě tehdy, když je uvnitř čtverce o straně
cm právě tehdy, když je uvnitř čtverce o straně 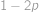 umístěného uprostřed (má-li tento čtverec nezápornou velikost). Pravděpodobnost spočítáme jako podíl obsahů, tedy
umístěného uprostřed (má-li tento čtverec nezápornou velikost). Pravděpodobnost spočítáme jako podíl obsahů, tedy
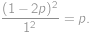
Tato kvadratická rovnice má dvě řešení:
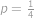
zadání vyhovuje,
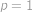
ne.
Ülesanne 21
Tabuľka 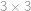 je vyplnená celými číslami. Súčty čísel v riadkoch zhora nadol stúpajú o
je vyplnená celými číslami. Súčty čísel v riadkoch zhora nadol stúpajú o  a súčty čísel v stĺpcoch zľava doprava sa zdvojnásobujú. Ak je súčet jedného z riadkov
a súčty čísel v stĺpcoch zľava doprava sa zdvojnásobujú. Ak je súčet jedného z riadkov 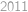 , tak aký je súčet čísel v ľavom stĺpci?
, tak aký je súčet čísel v ľavom stĺpci?
Peida / näita vastust
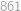 .
.
Ülesanne 22
Dva trajekty vyplávali naraz proti sebe cez zátoku. Oba plávali po priamke konštantnou, ale rozdielnou rýchlosťou. Prvýkrát sa stretli vo vzdialenosti 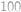 m od jedného brehu. Keď každý z nich doplával k protiľahlému brehu, ihneď sa otočil a plával rovnakou cestou naspäť. Na spiatočnej ceste sa stretli trajekty vo vzdialenosti
m od jedného brehu. Keď každý z nich doplával k protiľahlému brehu, ihneď sa otočil a plával rovnakou cestou naspäť. Na spiatočnej ceste sa stretli trajekty vo vzdialenosti 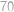 m od druhého brehu. Aká široká je zátoka?
m od druhého brehu. Aká široká je zátoka?
Peida / näita vastust
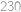 m.
m.
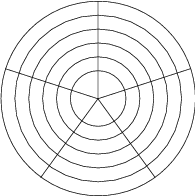
Ülesanne 23
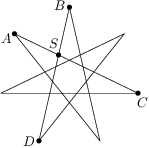
Vrcholy hviezdy na obrázku tvoria pravidelný sedemuholník. Aká je veľkosť vyznačeného uhla?
Peida / näita vastust
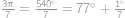 .
.
Označme body
 ,
, 
,
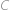 ,
, 
,
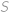
jako na obrázku. Pokud otočíme úsečku
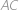
kolem středu hvězdy o
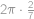
proti směru hodinových ručiček, dostaneme úsečku
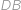 .
. Tedy
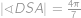 ,
, úhel
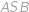
je pak jeho doplněk.
Ülesanne 24
Nájdite  spĺňajúce vzťah
spĺňajúce vzťah 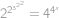 .
.
Poznámka: poschodové mocniny sa vyhodnocujú zhora, tj. 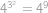 .
.
Peida / näita vastust
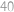 .
.
Upravíme pravou stranu rovnice:
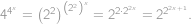
Požadované rovnosti tedy bude dosaženo, pokud
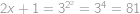 ,
, neboli
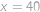 .
.
Ülesanne 25
Zistite počet usporiadaných trojíc prirodzených čísel 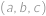 takých, že
takých, že 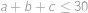 a
a
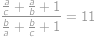
Peida / näita vastust
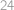 .
.
První jedničku zapíšeme jako 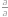 , druhou jako
, druhou jako 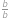 . Potom
. Potom
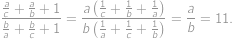
Pro
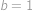 ,
, 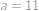
vyhovuje
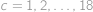
a pro
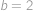 ,
, 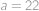
vyhovuje
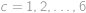 ,
, což dává celkem
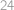
trojic.
Ülesanne 26
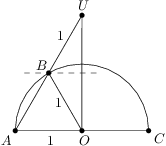
V rovine je daná kružnica s polomerom 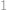 , stredom
, stredom  a priemerom
a priemerom 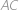 . Označme
. Označme 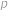 kolmicu na priemer
kolmicu na priemer 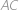 prechádzajúcu bodom
prechádzajúcu bodom  . Zvolíme bod
. Zvolíme bod 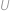 na priamke
na priamke 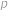 mimo kružnice taký, že ak označíme druhý priesečník kružnice s priamkou
mimo kružnice taký, že ak označíme druhý priesečník kružnice s priamkou 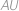 ako
ako  , tak platí
, tak platí 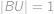 . Určte dĺžku úsečky
. Určte dĺžku úsečky 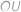 .
.
Peida / näita vastust
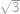 .
.
Jelikož
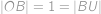 ,
, je trojúhelník
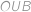
rovnoramenný. Bod

tak leží na ose odvěsny pravoúhlého trojúhelníku

a zároveň na jeho přeponě, takže je středem této přepony. Tím pádem i
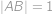
a z Pythagorovy věty dopočteme
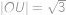 .
.
Ülesanne 27
Bitky dvoch armád  a
a  sa zúčastnilo dokopy
sa zúčastnilo dokopy 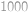 vojakov. Armády strieľali v salvách. V každej salve zastrelil každý vojak jedného vojaka z nepriateľskej armády (ak je to možné, tak každý iného). V tejto bitke strieľala najprv armáda
vojakov. Armády strieľali v salvách. V každej salve zastrelil každý vojak jedného vojaka z nepriateľskej armády (ak je to možné, tak každý iného). V tejto bitke strieľala najprv armáda  , potom armáda
, potom armáda  a nakoniec armáda
a nakoniec armáda  . Najmenej koľko vojakov bitku určite prežilo?
. Najmenej koľko vojakov bitku určite prežilo?
Peida / näita vastust
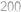 .
.
Ülesanne 28
Všetkých šesť strán konvexného šesťuholníka 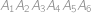 je zafarbených na červeno. Každú z uhlopriečok zafarbíme buď na červeno, alebo na modro. Koľko je zafarbení takých, že každý trojuholník
je zafarbených na červeno. Každú z uhlopriečok zafarbíme buď na červeno, alebo na modro. Koľko je zafarbení takých, že každý trojuholník 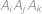 (
( ) má aspoň jednu zo svojich strán zafarbenú na červeno?
) má aspoň jednu zo svojich strán zafarbenú na červeno?
Peida / näita vastust
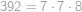 .
.
Ülesanne 29
Petržlen najskôr povedal jedno prirodzené číslo Škrečkovi a jedno prirodzené číslo Jefovi. Potom im povedal, že ich čísla sú rôzne a súčet ich čísel je dvojciferné číslo. Následne sa začali Škrečok s Jefom rozprávať:
Škrečok: „Neviem povedať, kto z nás má väčšie číslo.“
Jefo: „Ani ja, ale prezradím, že moje číslo je deliteľné 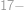 mi.“
mi.“
Škrečok: „Aha!, tak ja už teraz viem aký je súčet našich čísel.“
Čomu sa rovná tento súčet, ak obaja uvažovali bezchybne?
Peida / näita vastust
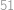 .
.
Ülesanne 30
V kaviarni sú Indovia a Turci a dohromady je ich 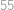 . Každý z nich pije buď kávu alebo čaj. Ind je pravdovravný práve vtedy, keď pije čaj. Turek je pravdovravný práve vtedy, keď pije kávu. Na otázky: „Pijete kávu?“, „Ste Turek?“ a „Prší vonku?“ boli počty kladných odpovedí postupne
. Každý z nich pije buď kávu alebo čaj. Ind je pravdovravný práve vtedy, keď pije čaj. Turek je pravdovravný práve vtedy, keď pije kávu. Na otázky: „Pijete kávu?“, „Ste Turek?“ a „Prší vonku?“ boli počty kladných odpovedí postupne 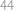 ,
,  a
a 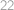 (každý odpovedal práve raz). Koľko Indov pije čaj? Nájdite všetky možnosti.
(každý odpovedal práve raz). Koľko Indov pije čaj? Nájdite všetky možnosti.
Peida / näita vastust
 .
.
Nejprve si uvědomíme, že na otázku „Pijete kávu?“ odpoví kladně právě Turci a na otázku „Jste Turek?“ odpoví kladně právě ti, kdo pijí kávu.
Víme tedy, že Turků je 44 a těch, kdo pijí kávu, je 33. Z toho dopočteme, že Indů je 11 a těch, kteří pijí čaj, je 22. Když sečteme počet Indů a počet lidí pijících čaj a odečteme od toho počet lidí, kteří lžou, dostaneme dvojnásobek počtu Indů pijících čaj.
Pokud venku prší, lže 33 lidí a čaj pije 0 Indů, pokud venku neprší, lže 22 lidí a čaj tak pije 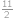 Indů. Necelou možnost kvůli humánnosti zavrhujeme.
Indů. Necelou možnost kvůli humánnosti zavrhujeme.
Ülesanne 31
Za pravý koniec prirodzeného čísla  v desiatkovom zápise boli dopísané tri cifry, čím vzniklo číslo, ktoré je súčtom všetkých prirodzených čísel od
v desiatkovom zápise boli dopísané tri cifry, čím vzniklo číslo, ktoré je súčtom všetkých prirodzených čísel od 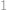 po
po  vrátane. Zistite všetky možné hodnoty čísla
vrátane. Zistite všetky možné hodnoty čísla  .
.
Peida / näita vastust
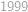 .
.
Označme  připsané trojčíslí. Jelikož
připsané trojčíslí. Jelikož 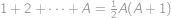 , máme dle zadání
, máme dle zadání
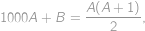
což upravíme na
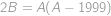 .
. Levá strana je alespoň

a nejvýše
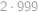 ,
, zatímco pravá strana je pro přirozené
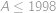
záporná a pro
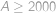
alespoň
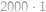 .
. Jediné možné
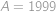
vyhovuje pro
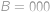 .
.
Ülesanne 32
Amanda, Bohumila, Celestína, Dobroslava a Etelka hrajú turnaj v štvorhre v stolnom tenise. Každá dvojica hrala proti každej inej dvojici práve raz. Amanda vyhrala dokopy 12 zápasov a Bohumila ich vyhrala 6. Koľko zápasov mohla vyhrať Celestína? Nájdite všetky možnosti.
Peida / näita vastust
 .
.
Spočítáme, kolik zápasů odehraje jedna hráčka. Chceme-li vytvořit zápas s danou hráčkou 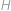 , vybereme si, která hráčka ze zbývajících hrát nebude (4 možnosti) a která z hrajících bude hrát s
, vybereme si, která hráčka ze zbývajících hrát nebude (4 možnosti) a která z hrajících bude hrát s 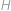 (3 možnosti). Každá hráčka tedy odehraje
(3 možnosti). Každá hráčka tedy odehraje 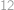 zápasů.
zápasů.
Z toho rovnou vidíme, že Adéla vyhrála všechno. Dále spočítáme, kolik zápasů hrála Adéla proti Báře. Máme tři možnosti, kdo může hrát s Adélou, pak 2 možnosti, kdo ze zbývajících může hrát s Bárou. Bára tedy prohrála 6 zápasů proti Adéle, všechny ostatní tak musela vyhrát.
Nyní už víme, jak poznat, která dvojice vyhrála. Je to ta, kde hrála Adéla, a byla-li Adéla mimo hru, vyhrála dvojice obsahující Báru.
Když hrála Cilka s Adélou, byly 3 možnosti, kdo je mimo hru, tedy takto vyhrála Cilka 3 zápasy. Když vyhrála Cilka s Bárou, byla mimo hru Adéla, to se stalo jednou. Celkem tak Cilka vyhrála 4 zápasy.
Ülesanne 33
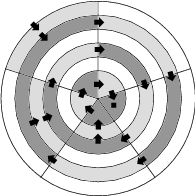
Dvaja hráči hrajú na uvedenom pláne pozostávajúceho z 30 políčok hru podľa nasledujúcich pravidiel:
- hráči sa striedajú v ťahoch,
- ťahom rozumieme vyfarbenie práve jedného políčka,
- v prvom ťahu sa vyfarbí políčko susediace s vonkajškom terča a v každom ďalšom ťahu sa vyfarbí políčko, ktoré susedí s posledným vyfarbeným políčkom a nie je ďalej od stredu,
- vyfarbené políčko sa nesmie znovu vyfarbovať,
- kto nemôže potiahnuť, prehral.
Koľko políčok bude vyfarbených na konci hry, v ktorej obaja hráči hrajú bezchybne a ten, kto nemôže vyhrať, sa snaží hru čo najviac predlžovať?
Peida / näita vastust
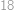 .
.
Jednotlivým mezikružím (včetně vnitřního kruhu) budeme říkat vrstvy, Za první považujeme tu na okraji, za šestou kruh uprostřed. Vrstvu s posledním vybarveným políčkem nazýváme aktuální.
Druhý hráč má následující vyhrávající strategii:
- Pokud je aktuální vrstva lichá, zahraje do následující vrstvy.
- v opačném případě v aktuální vrstvě zbývá licho volných políček, zahraje tedy do této vrstvy.
Touto strategií pošle vždy protihráče do pozice, kde je aktuální vrstva sudá a obsahuje sudo volných políček. Ten tak musí buď zahrát do liché vrstvy, nebo způsobit, že bude v aktuální vrstvě licho volných políček.
Druhý hráč přitom nemůže zahrát jinak, protože by mu tak mohl první hráč strategii převzít. První hráč bude hru prodlužovat tím, že bude oddalovat přesunutí se do další vrstvy. Hra tedy dopadne nějak takto:
Ülesanne 34
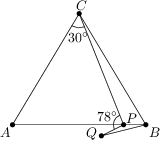
V trojuholníku 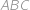 platí
platí 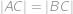 . Vo vnútri strany
. Vo vnútri strany 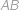 bližšie k bodu
bližšie k bodu  určíme bod
určíme bod 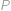 tak, aby
tak, aby 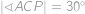 . Ďalej určíme bod
. Ďalej určíme bod  tak, aby
tak, aby 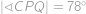 a aby body
a aby body 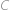 a
a  ležali v opačných polrovinách určených priamkou
ležali v opačných polrovinách určených priamkou 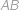 . Vieme, že všetky uhly v trojuholníkoch
. Vieme, že všetky uhly v trojuholníkoch 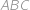 a
a 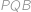 sú vyjadrené celočíselne v stupňoch. Zistite, aké hodnoty môže nadobúdať uhol
sú vyjadrené celočíselne v stupňoch. Zistite, aké hodnoty môže nadobúdať uhol 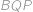 .
.
Peida / näita vastust
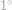 .
.
Jelikož

a
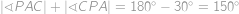 ,
, musí být
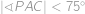 .
. Jeho velikost ve stupních je ale celočíselná, takže musí být dokonce
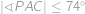
a
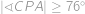 .
. Zároveň ale 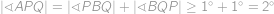 , z čehož
, z čehož
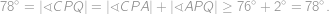
Ve všech neostrých nerovnostech tedy musela nastat rovnost a speciálně
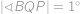 .
.
Ülesanne 35
Desať ľudí sedelo za radom vedľa seba v divadle. Po prestávke si sadli tak, že práve dvaja z nich zostali na svojich pôvodných miestach a zvyšných osem sa posadilo na stoličku jedného zo susedov. Koľkými spôsobmi to mohli urobiť?
Peida / näita vastust
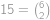 .
.
Ülesanne 36
Na každej stene kocky je napísané prirodzené číslo. Každému vrcholu kocky priradíme súčin čísel napísaných na troch príľahlých stenách. Vieme, že súčet čísel priradených vrcholom je 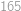 . Aké hodnoty môže nadobúdať súčet čísel na stenách?
. Aké hodnoty môže nadobúdať súčet čísel na stenách?
Peida / näita vastust
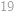 .
.
Označme čísla na stěnách písmeny  ,
, 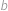 ,
,  ,
, 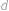 ,
,  ,
, 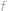 tak, aby proti sobě ležely dvojice
tak, aby proti sobě ležely dvojice  a
a 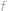 ,
, 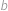 a
a  ,
,  a
a 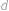 . Pak
. Pak
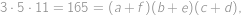
kde o druhé rovnosti se můžeme přesvědčit roznásobením. Jelikož čísla

až
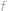
jsou přirozená, je každá závorka na pravé straně přirozená a větší než 1. Závorky se tedy (v nějakém pořadí) rovnají číslům
 ,
, 
a
 .
. Součet čísel na stěnách tak může být jedině
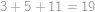 .
. Zkonstruovat příklad s požadovanými součty je snadné.
Ülesanne 37
Dvaja cyklisti pretekali na rovnej ulici v cestnom maratóne. Štartovali spoločne v rovnaký čas a z rovnakého konca ulice. Ak ľubovoľný z nich dorazil na ľubovoľný koniec ulice, tak sa otočil a išiel späť. Do okamihu, kým sa obaja zase stretli na jednom z koncov ulice, prešiel prvý z nich ulicu 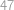 -krát a druhý
-krát a druhý 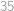 -krát. Koľkokrát sa počas tejto doby čelne minuli?
-krát. Koľkokrát sa počas tejto doby čelne minuli?
Peida / näita vastust
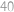 .
.
Na začátku jedou cyklisti stejným směrem. Pak se jeden z nich otočí, tedy pojedou proti sobě. Pak se čelně minou, tedy pojedou od sebe. Pak se jeden z nich otočí a jedou tak opět stejným směrem. Toto se opakuje, dokud neurazí své vzdálenosti, nakonec dorazí oba stejným směrem. V každém cyklu proběhnou dvě otočení se a jedno čelní minutí. První se otáčel 34 krát, druhý 46 krát, to je dohromady 80. Čelních minutí je pak dvakrát méně.
Ülesanne 38
Nájdite najväčšie prirodzené číslo také, že všetky cifry okrem prvej a poslednej sú menšie ako aritmetický priemer susedných dvoch cifier.
Peida / näita vastust
 .
.
Označme 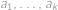 cifry hledaného čísla. Nejprve určíme maximální délku úseku, v němž cifry neklesají. Podmínku
cifry hledaného čísla. Nejprve určíme maximální délku úseku, v němž cifry neklesají. Podmínku  přepíšeme jako
přepíšeme jako 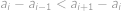 a interpretujeme tak, že postupně rostou rozdíly mezi po sobě jdoucími ciframi. Pokud by čísel v rostoucím úseku bylo alespoň
a interpretujeme tak, že postupně rostou rozdíly mezi po sobě jdoucími ciframi. Pokud by čísel v rostoucím úseku bylo alespoň  , byly by hodnoty rozdílů postupně rovny nejméně číslům
, byly by hodnoty rozdílů postupně rovny nejméně číslům 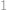 ,
,  ,
,  ,
,  a rozdíl mezi první a poslední cifrou by tak byl alespoň
a rozdíl mezi první a poslední cifrou by tak byl alespoň 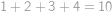 , což nelze. Každý rostoucí úsek má tedy nejvýše délku
, což nelze. Každý rostoucí úsek má tedy nejvýše délku  a zcela obdobně odvodíme, že i každý klesající úsek má nejvýše délku čtyři.
a zcela obdobně odvodíme, že i každý klesající úsek má nejvýše délku čtyři.
Jelikož rozdíly mezi po sobě jdoucími ciframi postupně rostou, nejdříve mohou být tyto rozdíly záporné — tam budou samotné cifry klesat, pak může být rozdíl jednou nulový a pak budou rozdíly kladné — tam budou samotné cifry růst. Odtud plyne, že hledané číslo se skládá z jednoho klesajícího úseku a jednoho rostoucího úseku a má tedy nejvýše  cifer. Nyní začneme osmiciferná čísla zkoušet od největších. Ta, která začínají dvojicemi cifer
cifer. Nyní začneme osmiciferná čísla zkoušet od největších. Ta, která začínají dvojicemi cifer 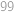 ,
, 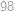 ,
, 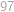 , nemohou tvořit dostatečně dlouhé klesající úseky a jako řešení tak nalézáme číslo
, nemohou tvořit dostatečně dlouhé klesající úseky a jako řešení tak nalézáme číslo  .
.
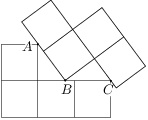
Ülesanne 39
Dve tetrisové kocky zostavené zo štvorcov o rozmeroch 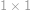 dm sa dotýkajú v bodoch
dm sa dotýkajú v bodoch  ,
,  ,
, 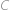 ako na obrázku. Určte vzdialenosť
ako na obrázku. Určte vzdialenosť 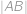 .
.
Peida / näita vastust
Peida / näita lahendust
Ülesanne 40
V rovine je daných 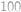 rôznych mrežových bodov. Každé dva rôzne body spojíme úsečkou. Najmenej koľko z týchto úsečiek má stred v mrežovom bode?
rôznych mrežových bodov. Každé dva rôzne body spojíme úsečkou. Najmenej koľko z týchto úsečiek má stred v mrežovom bode?
Poznámka: bod v rovine nazývame mrežový, ak sú obe jeho súradnice celočíselné.
Peida / näita vastust
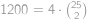 .
.
Souřadnice středu spojnice dvou mřížových bodů určíme jako průměr souřadnic těchto bodů. Všimneme si, že střed je opět mřížový bod právě tehdy, když mají vodorovné i svislé souřadnice obou bodů stejnou paritu. Všechny body se tedy podle parity souřadnic rozdělí do čtyř skupin (sudá-sudá, sudá-lichá, lichá-sudá, lichá-lichá), přičemž v každé skupině budou mít všechny spojnice za svůj střed mřížový bod a žádná spojnice bodů z různých skupin tuto vlastnost mít nebude. Aby byl počet úseček se středem v mřížovém bodě minimální, musí být všechny čtyři skupinky stejně velké. Rozmyslete si, že kdyby nebyly, tak přesunutím jednoho bodu z nejpočetnější skupiny do nejméně početné skupiny bychom počet takových úseček snížili. Počet spojnic v jedné skupince je tudíž 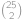 a celkem tedy bude úseček se středem v mřížovém bodě
a celkem tedy bude úseček se středem v mřížovém bodě 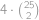 .
.
Ülesanne 41
Päťciferné číslo nazveme nerozložiteľné, ak sa nedá napísať ako súčin dvoch trojciferných čísel. Najviac koľko nerozložiteľných čísel môže nasledovať bezprostredne za sebou?
Peida / näita vastust
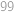 .
.
Ülesanne 42
Reálne čísla  a
a 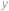 spĺňajú
spĺňajú 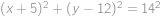 . Nájdite minimálnu hodnotu výrazu
. Nájdite minimálnu hodnotu výrazu  .
.
Peida / näita vastust
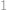 .
.
Ülesanne 43
Postupnosť vytvárame postupne pomocou vzorca
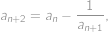
kým má pravá strana zmysel (tj. nedelí sa nulou). Navyše vieme, že
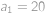
a
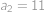 .
. Určte najmenšie

také, že
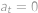 .
Peida / näita vastust
.
Peida / näita vastust
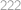 .
.
Dokud má pravá strana smysl, můžeme zadanou podmínku roznásobit a upravit na
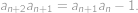
Vidíme, že
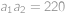 ,
, 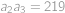
,
 ,
, 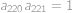
,
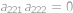 ,
, a proto
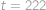 .
.
Ülesanne 44
Je daný ostrouhlý trojuholník 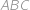 s výškami
s výškami 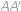 ,
, 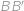 ,
, 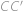 , ktoré sa pretínajú v bode
, ktoré sa pretínajú v bode 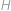 . Navyše platí
. Navyše platí
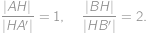
Určte
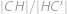 .
Peida / näita vastust
.
Peida / näita vastust
 .
.
Ülesanne 45
Na oslave každý (vrátane Ondra) pozná práve sedem chlapcov a presne desať dievčat. Známosti sú vzájomné a nikto nepozná sám seba. Koľko najmenej ľudí mohlo byť na oslave?
Peida / näita vastust
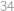 .
.
Označme počet chlapců  a počet dívek
a počet dívek 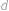 . Znání se mezi chlapci a dívkami je vzájemné, tedy sečteme-li přes všechny dívky chlapce, které znají, dostaneme totéž jako když sečteme přes všechny chlapce dívky, které znají. Máme tak
. Znání se mezi chlapci a dívkami je vzájemné, tedy sečteme-li přes všechny dívky chlapce, které znají, dostaneme totéž jako když sečteme přes všechny chlapce dívky, které znají. Máme tak 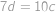 , z toho vidíme, že počet chlapců je přímo úměrný počtu dívek (stačí tedy minimalizovat počet dívek) a že počet dívek musí být dělitelný deseti. Každá dívka zná deset dívek, tedy
, z toho vidíme, že počet chlapců je přímo úměrný počtu dívek (stačí tedy minimalizovat počet dívek) a že počet dívek musí být dělitelný deseti. Každá dívka zná deset dívek, tedy 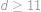 , nejmenší možný počet dívek tak je 20, chlapců pak je 14. A takovou situaci umíme sestrojit, např. následovně:
, nejmenší možný počet dívek tak je 20, chlapců pak je 14. A takovou situaci umíme sestrojit, např. následovně:
- Rozdělíme společnost do dvou skupinek po 10 dívkách a 7 chlapcích. V každé skupince seznámíme každého chlapce s každou dívkou.
- Postavíme dívky do kolečka. Pak každou seznámíme s deseti nejbližšími.
- Postavíme chlapce do kolečka. Pak každého seznámíme s šesti nejbližšími a dále s chlapcem naproti.
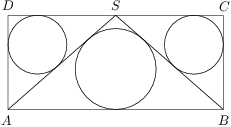
Ülesanne 46
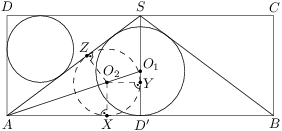
Bod 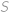 je stredom strany
je stredom strany  obdĺžnika
obdĺžnika 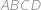 . Obe kružnice vpísané troj\-*uholníkom
. Obe kružnice vpísané troj\-*uholníkom 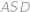 a
a 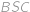 majú polomer
majú polomer  a kružnica vpísaná trojuholníku
a kružnica vpísaná trojuholníku 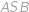 má polomer
má polomer  . Určte veľkosti strán obdĺžnika.
. Určte veľkosti strán obdĺžnika.
Peida / näita vastust
 ,
, 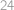 .
.
Označme body
 ,
, 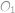
,
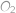 ,
, 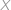
,
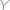 ,
, 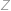
jako na obrázku a
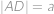 ,
, 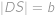
. Potom je
 ,
, takže poloměr kružnice vepsané trojúhelníku
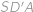
je
 .
. Navíc je tato kružnice vepsána úhlu
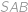 ,
, takže její střed
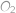
leží na přímce
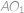 .
. Z podobnosti trojúhelníků
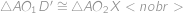
(věta

) máme
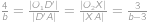 ,
, tj.
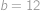 .
. Protože úseky tečen jsou shodné, platí 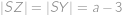 a
a 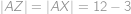 . Z Pythagorovy věty pro trojúhelník
. Z Pythagorovy věty pro trojúhelník 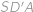 dostaneme druhou rovnici
dostaneme druhou rovnici 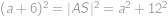 , odkud
, odkud 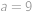 , takže strany obdélníku jsou
, takže strany obdélníku jsou  a
a 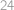 .
.
Ülesanne 47
Kladných deliteľov prirodzeného čísla  menších od
menších od  si napíšeme od najväčšieho po najmenšieho. Ak je súčet druhého a tretieho napísaného čísla rovný prvému napísanému číslu, tak číslo
si napíšeme od najväčšieho po najmenšieho. Ak je súčet druhého a tretieho napísaného čísla rovný prvému napísanému číslu, tak číslo  nazveme sčítacie. Koľko existuje sčítacích čísel menších ako
nazveme sčítacie. Koľko existuje sčítacích čísel menších ako 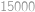 ?
?
Peida / näita vastust
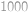 .
.
Vezmeme číslo  a zjistíme, co po něm požadujeme, aby bylo sčítací. Pokud by bylo liché, mělo by všechny dělitele liché. Ale to by pak součet dvou lichých čísel musel být liché číslo, což nejde. Číslo
a zjistíme, co po něm požadujeme, aby bylo sčítací. Pokud by bylo liché, mělo by všechny dělitele liché. Ale to by pak součet dvou lichých čísel musel být liché číslo, což nejde. Číslo  je tedy sudé.
je tedy sudé.
Všechny vypsané dělitele podělíme  . Tak získáme převrácené hodnoty všech dělitelů setříděných vzestupně, tentokrát kromě jedničky. Potřebujeme, aby součet převrácené hodnoty druhého a třetího nejmenšího dělitele dával jednu polovinu. Sčítance musí být různé, takže jeden z nich musí být větší než
. Tak získáme převrácené hodnoty všech dělitelů setříděných vzestupně, tentokrát kromě jedničky. Potřebujeme, aby součet převrácené hodnoty druhého a třetího nejmenšího dělitele dával jednu polovinu. Sčítance musí být různé, takže jeden z nich musí být větší než 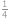 . Víme tak, že druhý nejmenší dělitel musí být roven třem. Třetí pak vyjde šest.
. Víme tak, že druhý nejmenší dělitel musí být roven třem. Třetí pak vyjde šest.
Tedy číslo  je „sčítací“ právě tehdy, když jeho dělitelé jsou vzestupně
je „sčítací“ právě tehdy, když jeho dělitelé jsou vzestupně 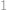 ,
,  ,
,  ,
,  , … neboli když je dělitelné šesti, ale ne čtyřmi ani pěti. Vydělíme všechna taková čísla z rozmezí
, … neboli když je dělitelné šesti, ale ne čtyřmi ani pěti. Vydělíme všechna taková čísla z rozmezí 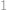 až
až 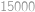 šesti a dostáváme všechna lichá čísla nedělitelná pěti v rozmezí
šesti a dostáváme všechna lichá čísla nedělitelná pěti v rozmezí 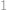 až
až 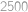 . Číslo je liché a nedělitelné pěti, pokud končí na jednu z cifer
. Číslo je liché a nedělitelné pěti, pokud končí na jednu z cifer 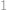 ,
,  ,
, 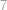 ,
,  . Mezi každými deseti po sobě jdoucími čísly jsou taková čísla
. Mezi každými deseti po sobě jdoucími čísly jsou taková čísla  . To máme
. To máme 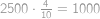 sčítacích čísel.
sčítacích čísel.
Ülesanne 48
Nájdite všetky reálne čísla  spĺňajúce vzťah
spĺňajúce vzťah
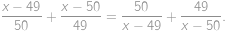
Peida / näita vastust
Peida / näita lahendust
Ülesanne 49
Umiestnenie hodinovej a minútovej ručičky na ciferníku nazývame korektné, ak vyjadruje skutočný čas v priebehu dňa. Zistite, koľko existuje takých korektných umiestnení, ktoré zostanú korektné aj po zámene ručičiek.
Peida / näita vastust
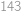 .
.
Označme  , resp.
, resp.  úhly měřené ve stupních (
úhly měřené ve stupních ( ), které svírají hodinová, resp. minutová ručička se spojnicí středu a dvanáctky. Uvědomíme si, že umístění ručiček je platné, právě když existuje celé
), které svírají hodinová, resp. minutová ručička se spojnicí středu a dvanáctky. Uvědomíme si, že umístění ručiček je platné, právě když existuje celé  takové, že
takové, že
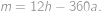
Aby umístění ručiček zůstalo platné i po jejich prohození, musí existovat celé
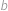
takové, že
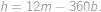
Dosazením první rovnice do druhé dostáváme
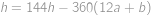
a jednoduchou úpravou
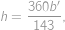
kde
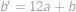
je rovněž celočíselné. Poslední rovnice má pro

z intervalu
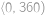
právě
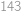
řešení, která nalezneme pro
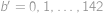 .
. A protože pro každé

dostáváme z první rovnice jednoznačně určené

z intervalu
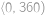 ,
, existuje právě
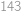
hledaných dvojic
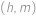 .
.
Ülesanne 50
Nech  ,
, 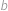 ,
,  sú také nenulové reálne čísla, že kvadratické trojčleny
sú také nenulové reálne čísla, že kvadratické trojčleny 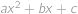 a
a 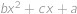 majú spoločný koreň. Určte, aké hodnoty môže tento spoločný koreň nadobúdať.
majú spoločný koreň. Určte, aké hodnoty môže tento spoločný koreň nadobúdať.
Peida / näita vastust
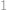 .
.
Ülesanne 51
Nájdite všetky celé čísla  také, že obe čísla
také, že obe čísla 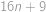 a
a 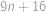 sú druhými mocninami nejakých prirodzených čísel.
sú druhými mocninami nejakých prirodzených čísel.
Peida / näita vastust
Peida / näita lahendust
Má-li  má požadovanou vlastnost, pak jsou druhými mocninami i čísla
má požadovanou vlastnost, pak jsou druhými mocninami i čísla

Hledejme tedy dvě druhé mocniny, které se liší o
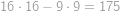
. Pro přirozená

řešíme rovnici
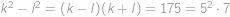
a postupně vyzkoušíme možné rozklady čísla
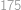 .
. Řešení
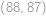 ,
, 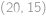
,
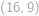
postupně odpovídají hodnotám
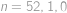 ,
, které jsou skutečně řešením.
Ülesanne 52
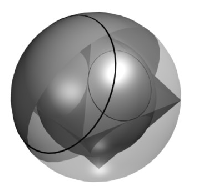
Je daný pravidelný osemsten s hranou dĺžky  . Jednej jeho stene vpíšeme kružnicu a stene s ňou susediacej kružnicu opíšeme. Aká je najmenšia vzdialenosť medzi týmito dvoma kružnicami?
. Jednej jeho stene vpíšeme kružnicu a stene s ňou susediacej kružnicu opíšeme. Aká je najmenšia vzdialenosť medzi týmito dvoma kružnicami?
Peida / näita vastust
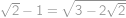 .
.
Přikreslíme si do obrázku dvě sféry. Jednu osmistěnu opíšeme a druhou vepíšeme jeho hranám. Celá opsaná kružnice tak leží na opsané sféře a celá vepsaná kružnice na vepsané sféře.
Nejmenší vzdálenost kružnic tak určitě nebude menší než nejmenší vzdálenost sfér. Nejmenší vzdálenost soustředných sfér je rovna rozdílu jejich poloměrů, tedy 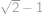 .
.
Zbývá si uvědomit, že této vzdálenosti se skutečně nabývá. To nastane, pokud existuje polopřímka s počátkem ve středu osmistěnu, která prochází oběma kružnicemi. Můžeme snadno najít polopřímku protínající vepsanou kružnici, která vede vnitřkem opsané kružnice, i takovou, která opsanou zvenku míjí. Bude tedy existovat i taková polopřímka, co opsanou kružnici protíná.
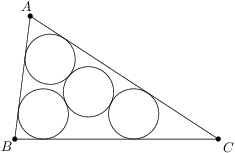
Ülesanne 53
Je daný trojuholník 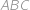 s polomerom opísanej kružnice
s polomerom opísanej kružnice  a polomerom vpísanej kružnice
a polomerom vpísanej kružnice  . Vnútri trojuholníka sú do uhlov
. Vnútri trojuholníka sú do uhlov 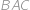 ,
,  ,
, 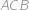 vpísané zhodné kružnice s polomerom
vpísané zhodné kružnice s polomerom  tak, že existuje ďalšia kružnica s polomerom
tak, že existuje ďalšia kružnica s polomerom  , ktorá má so všetkými z nich vonkajší dotyk. Určte
, ktorá má so všetkými z nich vonkajší dotyk. Určte  .
.
Peida / näita vastust
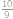 .
.
Ülesanne 54
Pre reálne čísla  ,
, 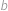 ,
,  ,
, 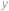 platí
platí
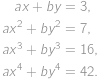
Určte hodnotu
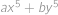 .
Peida / näita vastust
.
Peida / näita vastust
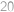 .
.
Rozmyslíme si, že pro každé přirozené  platí
platí
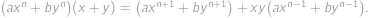
Označme
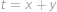 ,
, 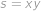
a dosaďme do předchozího vztahu postupně
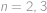 .
. Dostaneme tak soustavu lineárních rovnic
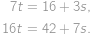
Řešením soustavy jsou
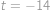 ,
, 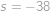
. Nakonec stačí do prvního vztahu dosadit
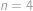 ,
, čímž dostaneme
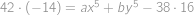
a dopočteme
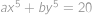 .
.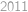 .
.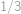 .
.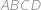 kružnicu v bodoch
kružnicu v bodoch 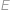 ,
,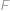 ,
, 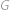 ,
,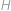 . Vieme, že
. Vieme, že 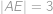 ,
,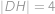 a
a 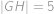 . Vypočítajte dĺžku úsesčky
. Vypočítajte dĺžku úsesčky 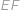 .
.
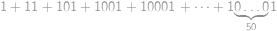 .
.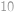 mandaríniek menej ako v zvyšných dvoch sáčkoch dohromady. Koľko mandaríniek je v treťom sáčku?
mandaríniek menej ako v zvyšných dvoch sáčkoch dohromady. Koľko mandaríniek je v treťom sáčku? ,
, ,
, 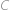 ,
, rovnako ako na obrázku. Obvody obdĺžnikov
rovnako ako na obrázku. Obvody obdĺžnikov  ,
, a
a 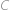 sú po rade
sú po rade  cm,
cm, cm a
cm a 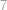 cm.
cm. ?
?
 ,
, a
a 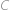 (v desiatkovej sústave) také, aby platil nasledujúci sčítací vzťah:
(v desiatkovej sústave) také, aby platil nasledujúci sčítací vzťah: 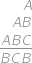
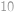 cm
cm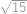 cm.
cm.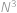 rovnako veľkých kociek a postavil z nich jednu veľkú kocku o rozmeroch
rovnako veľkých kociek a postavil z nich jednu veľkú kocku o rozmeroch 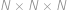 .
.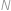 ,
,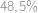 ,
,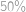 ?
? ,
,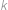 ,
,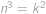 .
. a
a 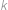 ,
,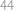 úloh (vrátane tejto).
úloh (vrátane tejto). spĺňajúce vzťah
spĺňajúce vzťah 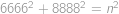 .
.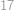 ,
,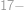 timi
timi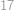 .
.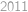 -ciferného
-ciferného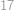 alebo
alebo 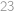 .
.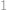 .
. ,
,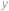 ,
,  spĺňajú
spĺňajú 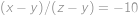 .
.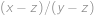 ?
?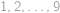 napíšeme za sebou v nejakom poradí tak, aby vzniklo deväťciferné číslo. Uvažujme všetky trojice po sebe idúcich cifier tohto čísla a k týmto trojiciam zodpovedajúce trojciferné čísla sčítame. Aký najväčší výsledok môžeme dostať?
napíšeme za sebou v nejakom poradí tak, aby vzniklo deväťciferné číslo. Uvažujme všetky trojice po sebe idúcich cifier tohto čísla a k týmto trojiciam zodpovedajúce trojciferné čísla sčítame. Aký najväčší výsledok môžeme dostať?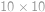 je napísané číslo. Filip si vybral dve čísla z tabuľky a do zošita si napísal ich súčin. Toto spravil pre všetky dvojice čísel z tabuľky. Všimol si, že práve
je napísané číslo. Filip si vybral dve čísla z tabuľky a do zošita si napísal ich súčin. Toto spravil pre všetky dvojice čísel z tabuľky. Všimol si, že práve 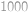 z týchto súčinov je záporných. Koľko z pôvodných čísel mohlo byť rovných nule? Vypíšte všetky možnosti.
z týchto súčinov je záporných. Koľko z pôvodných čísel mohlo byť rovných nule? Vypíšte všetky možnosti.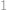 fufeň. Každý ďalší deň razili mince v najmenšej hodnote, ktorá sa nedala zaplatiť pomocou maximálne desiatich už vyrazených mincí. Mince akej hodnoty razili počas
fufeň. Každý ďalší deň razili mince v najmenšej hodnote, ktorá sa nedala zaplatiť pomocou maximálne desiatich už vyrazených mincí. Mince akej hodnoty razili počas  -teho
-teho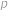 riešenie úlohy na tomto papieri. Určte pravdepodobnosť (číslo z intervalu
riešenie úlohy na tomto papieri. Určte pravdepodobnosť (číslo z intervalu 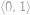 ),
),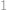 cm
cm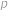 cm.
cm.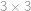 je vyplnená celými číslami. Súčty čísel v riadkoch zhora nadol stúpajú o
je vyplnená celými číslami. Súčty čísel v riadkoch zhora nadol stúpajú o  a súčty čísel v stĺpcoch zľava doprava sa zdvojnásobujú. Ak je súčet jedného z riadkov
a súčty čísel v stĺpcoch zľava doprava sa zdvojnásobujú. Ak je súčet jedného z riadkov 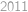 ,
,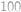 m
m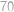 m
m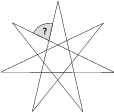
 spĺňajúce vzťah
spĺňajúce vzťah 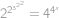 .
.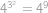 .
.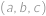 takých, že
takých, že 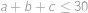 a
a 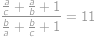
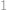 ,
, a priemerom
a priemerom 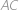 .
.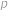 kolmicu na priemer
kolmicu na priemer 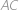 prechádzajúcu bodom
prechádzajúcu bodom  .
.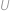 na priamke
na priamke 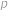 mimo kružnice taký, že ak označíme druhý priesečník kružnice s priamkou
mimo kružnice taký, že ak označíme druhý priesečník kružnice s priamkou 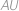 ako
ako  ,
,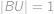 .
.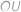 .
. a
a  sa zúčastnilo dokopy
sa zúčastnilo dokopy 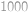 vojakov. Armády strieľali v salvách. V každej salve zastrelil každý vojak jedného vojaka z nepriateľskej armády (ak je to možné, tak každý iného). V tejto bitke strieľala najprv armáda
vojakov. Armády strieľali v salvách. V každej salve zastrelil každý vojak jedného vojaka z nepriateľskej armády (ak je to možné, tak každý iného). V tejto bitke strieľala najprv armáda  ,
, a nakoniec armáda
a nakoniec armáda  .
.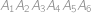 je zafarbených na červeno. Každú z uhlopriečok zafarbíme buď na červeno, alebo na modro. Koľko je zafarbení takých, že každý trojuholník
je zafarbených na červeno. Každú z uhlopriečok zafarbíme buď na červeno, alebo na modro. Koľko je zafarbení takých, že každý trojuholník 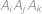 (
( ) má aspoň jednu zo svojich strán zafarbenú na červeno?
) má aspoň jednu zo svojich strán zafarbenú na červeno?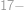 mi.“
mi.“ .
. ,
, a
a  (každý odpovedal práve raz). Koľko Indov pije čaj? Nájdite všetky možnosti.
(každý odpovedal práve raz). Koľko Indov pije čaj? Nájdite všetky možnosti. v desiatkovom zápise boli dopísané tri cifry, čím vzniklo číslo, ktoré je súčtom všetkých prirodzených čísel od
v desiatkovom zápise boli dopísané tri cifry, čím vzniklo číslo, ktoré je súčtom všetkých prirodzených čísel od  po
po  vrátane. Zistite všetky možné hodnoty čísla
vrátane. Zistite všetky možné hodnoty čísla  .
.
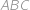 platí
platí 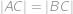 .
.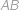 bližšie k bodu
bližšie k bodu  určíme bod
určíme bod 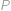 tak, aby
tak, aby 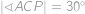 .
. tak, aby
tak, aby 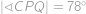 a aby body
a aby body 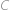 a
a  ležali v opačných polrovinách určených priamkou
ležali v opačných polrovinách určených priamkou 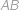 .
.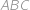 a
a 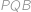 sú vyjadrené celočíselne v stupňoch. Zistite, aké hodnoty môže nadobúdať uhol
sú vyjadrené celočíselne v stupňoch. Zistite, aké hodnoty môže nadobúdať uhol 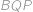 .
.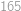 .
.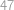 -krát
-krát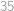 -krát.
-krát.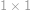 dm sa dotýkajú v bodoch
dm sa dotýkajú v bodoch  ,
, ,
,  ako na obrázku. Určte vzdialenosť
ako na obrázku. Určte vzdialenosť 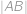 .
.
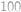 rôznych mrežových bodov. Každé dva rôzne body spojíme úsečkou. Najmenej koľko z týchto úsečiek má stred v mrežovom bode?
rôznych mrežových bodov. Každé dva rôzne body spojíme úsečkou. Najmenej koľko z týchto úsečiek má stred v mrežovom bode?  a
a 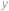 spĺňajú
spĺňajú 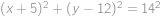 .
. .
.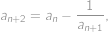
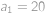 a
a 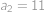 .
. také, že
také, že 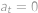 .
.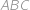 s výškami
s výškami 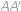 ,
,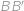 ,
, 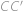 ,
,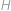 .
.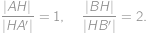
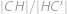 .
.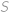 je stredom strany
je stredom strany  obdĺžnika
obdĺžnika 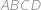 .
.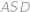 a
a 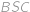 majú polomer
majú polomer  a kružnica vpísaná trojuholníku
a kružnica vpísaná trojuholníku 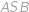 má polomer
má polomer  .
.
 menších od
menších od  si napíšeme od najväčšieho po najmenšieho. Ak je súčet druhého a tretieho napísaného čísla rovný prvému napísanému číslu, tak číslo
si napíšeme od najväčšieho po najmenšieho. Ak je súčet druhého a tretieho napísaného čísla rovný prvému napísanému číslu, tak číslo  nazveme sčítacie. Koľko existuje sčítacích čísel menších ako
nazveme sčítacie. Koľko existuje sčítacích čísel menších ako 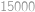 ?
? spĺňajúce vzťah
spĺňajúce vzťah 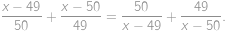
 ,
,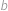 ,
,  sú také nenulové reálne čísla, že kvadratické trojčleny
sú také nenulové reálne čísla, že kvadratické trojčleny 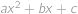 a
a 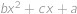 majú spoločný koreň. Určte, aké hodnoty môže tento spoločný koreň nadobúdať.
majú spoločný koreň. Určte, aké hodnoty môže tento spoločný koreň nadobúdať. také, že obe čísla
také, že obe čísla 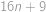 a
a 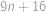 sú druhými mocninami nejakých prirodzených čísel.
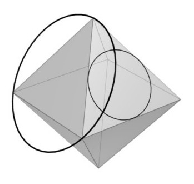
sú druhými mocninami nejakých prirodzených čísel. .
.
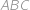 s polomerom opísanej kružnice
s polomerom opísanej kružnice  a polomerom vpísanej kružnice
a polomerom vpísanej kružnice  .
. ,
, ,
,  vpísané zhodné kružnice s polomerom
vpísané zhodné kružnice s polomerom  tak, že existuje ďalšia kružnica s polomerom
tak, že existuje ďalšia kružnica s polomerom  ,
, .
.
 ,
, ,
,  ,
,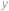 platí
platí 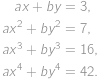
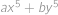 .
.
 .
.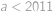 splňující nerovnici
splňující nerovnici 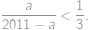
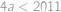 a vidíme, že největší vyhovující
a vidíme, že největší vyhovující 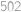 a výsledný zlomek je pak roven
a výsledný zlomek je pak roven 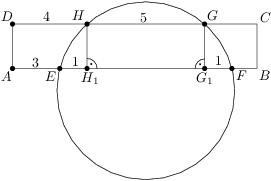
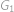 ,
,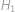 po řadě průměty bodů
po řadě průměty bodů 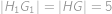 .
.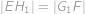 a navíc
a navíc 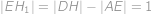 .
.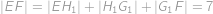 .
.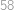 .
.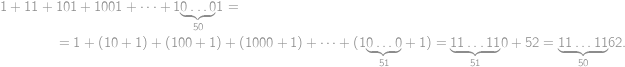
 .
.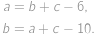
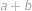 a dopočteme
a dopočteme 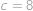 .
. však nevyhovují, protože v obou případech by na počátku musel být počet ořechů v první hromádce záporný. Počáteční situace se
však nevyhovují, protože v obou případech by na počátku musel být počet ořechů v první hromádce záporný. Počáteční situace se  ,
, 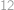 a
a 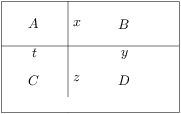
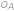 ,
,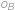 ,
,  ,
,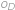 pak platí
pak platí 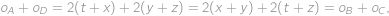
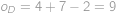 cm.
cm.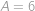 ,
,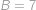 ,
, 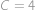 .
.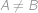 ,
,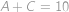 ,
,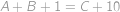 a
a 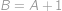 .
. .
.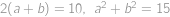 .
.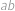 určíme například pomocí
určíme například pomocí 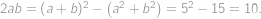
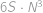 a povrch velké krychle je
a povrch velké krychle je 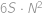 .
.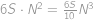 .
.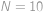 .
.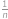 (například pro
(například pro 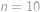 se od čísla
se od čísla 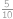 odchýlíme o
odchýlíme o 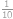 k číslu
k číslu 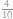 ),
),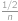 (pro
(pro 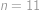 od
od 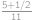 k
k 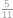 ). Odtud vidíme, že je výhodnější hledat lichá
). Odtud vidíme, že je výhodnější hledat lichá 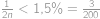 ,
,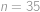 .
.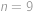 ,
,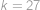 .
.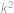 bylo třetí mocninou přirozeného čísla, musí být rovněž
bylo třetí mocninou přirozeného čísla, musí být rovněž 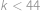 je
je 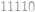 .
.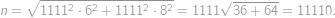
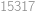 .
.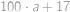 pro nějaké
pro nějaké 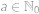 .
.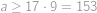 ,
,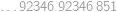 . Zbývá dopočítat, že
. Zbývá dopočítat, že 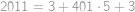 ,
,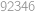 .
.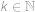 existuje právě jedno nejmenší číslo s tímto ciferným součtem, a tedy i právě jedno luxusní číslo. Označme ho
existuje právě jedno nejmenší číslo s tímto ciferným součtem, a tedy i právě jedno luxusní číslo. Označme ho 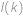 .
.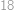 ,
,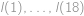 nejvýše dvojciferná. Protože ciferné součty trojciferných čísel nabývají všech hodnot od
nejvýše dvojciferná. Protože ciferné součty trojciferných čísel nabývají všech hodnot od 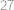 ,
, trojciferná a je jich
trojciferná a je jich 
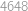 .
.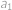 ,
,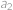 , … ,
, … , 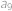 .
.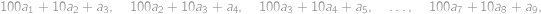
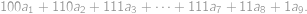
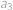 až
až 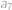 .
.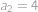 ,
,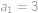 ,
, 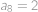 ,
,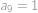 . Součet vyjde
. Součet vyjde 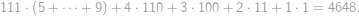
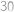 ,
,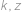 počty kladných, resp. záporných čísel a
počty kladných, resp. záporných čísel a 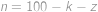 počet nul. Součin dvou čísel je záporný, právě když je jedno z nich kladné a druhé záporné. Počet možností, jak vybrat jedno kladné číslo z
počet nul. Součin dvou čísel je záporný, právě když je jedno z nich kladné a druhé záporné. Počet možností, jak vybrat jedno kladné číslo z 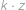 .
.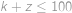 tedy musí platit i
tedy musí platit i 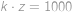 .
.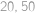 a
a 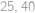 skýtající postupně
skýtající postupně 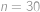 ,
,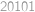 (fufníků).
(fufníků).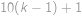 .
.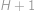 až
až 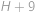 .
.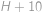 zaplatit nelze, neboť jak požadovaná částka, tak hodnoty všech doposud vyrobených mincí dávají po dělení deseti zbytek
zaplatit nelze, neboť jak požadovaná částka, tak hodnoty všech doposud vyrobených mincí dávají po dělení deseti zbytek 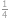 .
.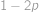 umístěného uprostřed (má-li tento čtverec nezápornou velikost). Pravděpodobnost spočítáme jako podíl obsahů, tedy
umístěného uprostřed (má-li tento čtverec nezápornou velikost). Pravděpodobnost spočítáme jako podíl obsahů, tedy 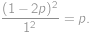
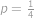 zadání vyhovuje,
zadání vyhovuje, 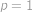 ne.
ne.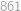 .
.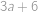 (sčítáme-li po řádcích) a
(sčítáme-li po řádcích) a 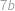 (sčítáme-li po sloupcích). Tedy
(sčítáme-li po sloupcích). Tedy 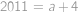 .
.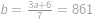 .
.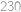 m.
m.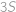 metrů. Jelikož trajekty jedou konstantními rychlostmi, nastalo jejich druhé setkání po třikrát delším čase než to první. Pro ten trajekt, který do prvního setkání najel
metrů. Jelikož trajekty jedou konstantními rychlostmi, nastalo jejich druhé setkání po třikrát delším čase než to první. Pro ten trajekt, který do prvního setkání najel 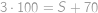 ,
,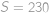 plyne bezprostředně.
plyne bezprostředně.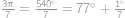 .
.
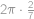 proti směru hodinových ručiček, dostaneme úsečku
proti směru hodinových ručiček, dostaneme úsečku 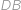 .
.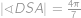 ,
,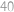 .
.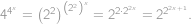
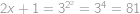 ,
,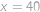 .
.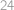 .
.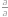 ,
,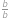 .
.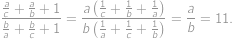
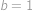 ,
,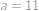 vyhovuje
vyhovuje 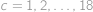 a pro
a pro 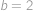 ,
,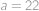 vyhovuje
vyhovuje 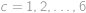 ,
,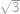 .
.
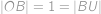 ,
,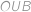 rovnoramenný. Bod
rovnoramenný. Bod  a zároveň na jeho přeponě, takže je středem této přepony. Tím pádem i
a zároveň na jeho přeponě, takže je středem této přepony. Tím pádem i 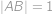 a z Pythagorovy věty dopočteme
a z Pythagorovy věty dopočteme 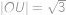 .
.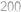 .
.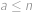 ) v armádě
) v armádě 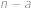 v armádě
v armádě 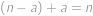 a počet vojáků v
a počet vojáků v  vojáků. Konečně před první salvou bylo v
vojáků. Konečně před první salvou bylo v  vojáků a v
vojáků a v 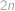 vojáků.
vojáků. 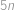 vojáků, tj.
vojáků, tj. 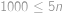 a máme
a máme 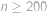 .
.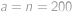 se každé maximální hodnoty nabyde.
se každé maximální hodnoty nabyde.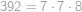 .
.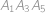 a
a 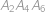 (na obrázku čárkovaně) všechny ostatní trojúhelníky již mají červenou hranu. Každý čárkovaný trojúhelník můžeme obarvit
(na obrázku čárkovaně) všechny ostatní trojúhelníky již mají červenou hranu. Každý čárkovaný trojúhelník můžeme obarvit 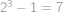 způsoby, protože nemůžeme všechny jeho hrany obarvit modře. Nakonec ještě můžeme dohromady
způsoby, protože nemůžeme všechny jeho hrany obarvit modře. Nakonec ještě můžeme dohromady 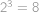 způsoby obarvit tečkovaně vyznačené úhlopříčky
způsoby obarvit tečkovaně vyznačené úhlopříčky 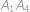 ,
,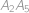 ,
,  .
.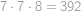 vyhovujících obarvení.
vyhovujících obarvení. 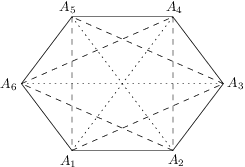
 .
.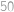 .
.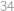 .
. .
.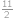 Indů. Necelou možnost kvůli humánnosti zavrhujeme.
Indů. Necelou možnost kvůli humánnosti zavrhujeme.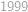 .
.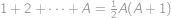 ,
,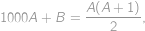
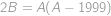 .
.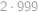 ,
,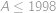 záporná a pro
záporná a pro 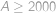 alespoň
alespoň 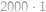 .
.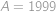 vyhovuje pro
vyhovuje pro  .
.
 .
.
 a
a 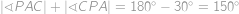 ,
,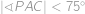 .
.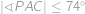 a
a 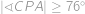 .
.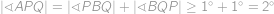 ,
,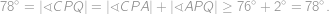
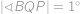 .
.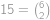 .
.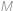 (reprezentující situaci, kdy člověk zůstal na svém místě). Počet vyhovujících rozsazení pak musí být roven počtu takovýchto posloupností, to jest
(reprezentující situaci, kdy člověk zůstal na svém místě). Počet vyhovujících rozsazení pak musí být roven počtu takovýchto posloupností, to jest 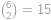 .
.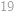 .
.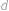 ,
,  ,
,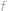 tak, aby proti sobě ležely dvojice
tak, aby proti sobě ležely dvojice 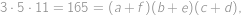
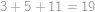 .
. .
.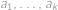 cifry hledaného čísla. Nejprve určíme maximální délku úseku, v němž cifry neklesají. Podmínku
cifry hledaného čísla. Nejprve určíme maximální délku úseku, v němž cifry neklesají. Podmínku  přepíšeme jako
přepíšeme jako 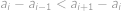 a interpretujeme tak, že postupně rostou rozdíly mezi po sobě jdoucími ciframi. Pokud by čísel v rostoucím úseku bylo alespoň
a interpretujeme tak, že postupně rostou rozdíly mezi po sobě jdoucími ciframi. Pokud by čísel v rostoucím úseku bylo alespoň 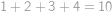 ,
,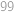 ,
,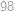 ,
,  ,
, dm
dm 
 dm.
dm.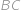 jsou shodné podle věty
jsou shodné podle věty 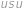 .
. a podle Pythagorovy věty také
a podle Pythagorovy věty také 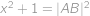 .
.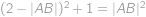 .
.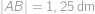 .
.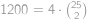 .
.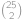 a celkem tedy bude úseček se středem v mřížovém bodě
a celkem tedy bude úseček se středem v mřížovém bodě 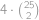 .
.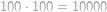 a
a 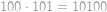 jsou dvě nejmenší rozkládací pěticiferná čísla. Tedy
jsou dvě nejmenší rozkládací pěticiferná čísla. Tedy 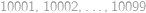 tvoří posloupnost
tvoří posloupnost 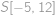 a poloměrem
a poloměrem 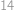 .
.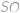 s kružnicí
s kružnicí 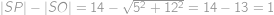 .
.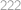 .
.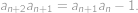
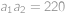 ,
,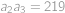 ,
,  ,
,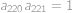 ,
, 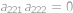 ,
,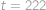 .
.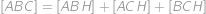 .
.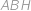 mají společnou stranu
mají společnou stranu 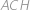 a
a 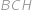 ,
,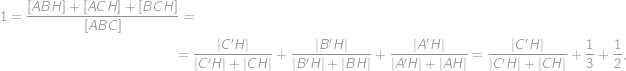
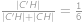 a
a 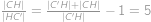 .
.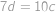 ,
,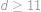 ,
,
 ,
,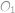 ,
, 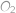 ,
,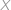 ,
, 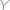 ,
,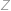 jako na obrázku a
jako na obrázku a 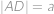 ,
,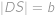 . Potom je
. Potom je  ,
,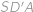 je
je 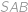 ,
,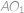 .
.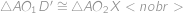 (věta
(věta  ) máme
) máme 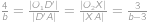 ,
,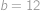 .
.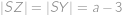 a
a 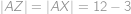 .
.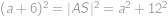 ,
,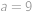 ,
,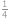 .
. , … neboli když je dělitelné šesti, ale ne čtyřmi ani pěti. Vydělíme všechna taková čísla z rozmezí
, … neboli když je dělitelné šesti, ale ne čtyřmi ani pěti. Vydělíme všechna taková čísla z rozmezí 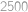 .
.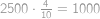 sčítacích čísel.
sčítacích čísel.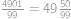 .
.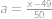 a
a 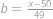 .
.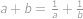 .
.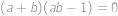 ,
,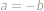 je lineární vzhledem k
je lineární vzhledem k 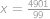 .
.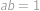 je kvadratická vzhledem k
je kvadratická vzhledem k 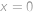 a
a 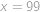 .
.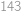 .
. ,
, úhly měřené ve stupních (
úhly měřené ve stupních ( ), které svírají hodinová, resp. minutová ručička se spojnicí středu a dvanáctky. Uvědomíme si, že umístění ručiček je platné, právě když existuje celé
), které svírají hodinová, resp. minutová ručička se spojnicí středu a dvanáctky. Uvědomíme si, že umístění ručiček je platné, právě když existuje celé 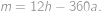
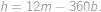
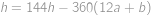
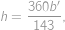
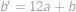 je rovněž celočíselné. Poslední rovnice má pro
je rovněž celočíselné. Poslední rovnice má pro 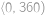 právě
právě 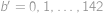 .
.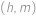 .
.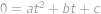 a
a 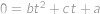 ,
,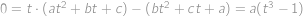 .
.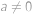 ,
,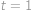 .
.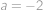 ,
,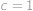 zjišťujeme, že jednička také společným kořenem být může.
zjišťujeme, že jednička také společným kořenem být může.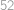 .
.
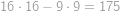 . Pro přirozená
. Pro přirozená  řešíme rovnici
řešíme rovnici 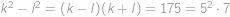 a postupně vyzkoušíme možné rozklady čísla
a postupně vyzkoušíme možné rozklady čísla 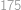 .
.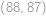 ,
,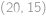 ,
, 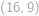 postupně odpovídají hodnotám
postupně odpovídají hodnotám 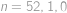 ,
,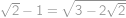 .
.
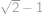 .
. .
.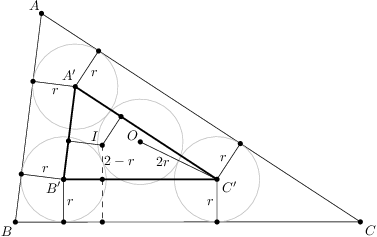
 ,
, ,
, 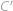 středy kružnic vepsaných do úhlů
středy kružnic vepsaných do úhlů 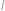 střed kružnice vepsané trojúhelníku
střed kružnice vepsané trojúhelníku 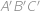 mají rovnoběžné odpovídající si strany, takže jsou si podobné. Vyjádřeme poloměry kružnice vepsané a opsané trojúhelníku
mají rovnoběžné odpovídající si strany, takže jsou si podobné. Vyjádřeme poloměry kružnice vepsané a opsané trojúhelníku 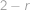 ,
,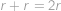 ,
,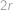 .
.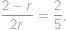
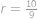 .
.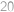 .
.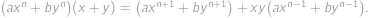
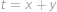 ,
,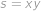 a dosaďme do předchozího vztahu postupně
a dosaďme do předchozího vztahu postupně 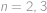 .
.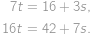
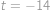 ,
,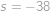 . Nakonec stačí do prvního vztahu dosadit
. Nakonec stačí do prvního vztahu dosadit 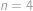 ,
,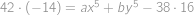 a dopočteme
a dopočteme 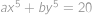 .
.



















