Problem 1J
If we increase the length of each edge of a cube by 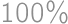 ,
,
Show / hide solution
Problem 2J
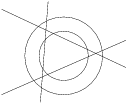
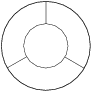
What is the largest number of pieces a ring can be divided into using three straight lines?

Show / hide solution
Problem 3J
A five digit number 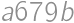 is divisible by
is divisible by 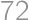 .
.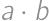 .
.
Show / hide solution
Problem 4J
A math teacher decided to organize two rounds of a math competition. Each team consisted of five members. In the first round, the students divided themselves into teams on their own. In the second round the teacher divided them so that nobody was in the same team with anyone he or she has played with in the first round. Determine the minimum number of students in which such division is possible.
Show / hide answerShow / hide solution
Problem 5J
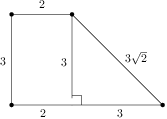
The whole surface of a rectangular prism-shaped vanilla cake with edges of lengths 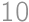 ,
,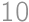 and
and 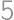 is covered by a thin layer of chocolate. Let us cut the cake into cubes of volume
is covered by a thin layer of chocolate. Let us cut the cake into cubes of volume 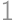 .
.
Show / hide solution
Problem 6J
We are given a square 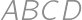 with side length
with side length 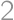 and a point
and a point 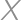 in its plane (outside the square) so that
in its plane (outside the square) so that 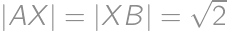 .
.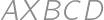 ?
?
Show / hide solution
Problem 7J
Jacob had written 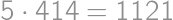 on a blackboard. Now he is wondering how to increase or decrease each of the digits by
on a blackboard. Now he is wondering how to increase or decrease each of the digits by 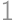 so that the result is correct. What will be the right-hand side after the change?
so that the result is correct. What will be the right-hand side after the change?
Show / hide solution
Problem 8J
The sum of integers  and
and 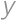 is at most
is at most 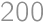 and their difference is smaller than
and their difference is smaller than 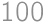 .
.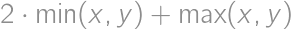 .
.
Show / hide solution
Problem 9J
Let 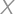 ,
, ,
,  be real numbers such that the arithmetic mean of
be real numbers such that the arithmetic mean of  and
and 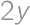 is equal to
is equal to 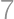 ,
, and
and 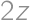 is equal to
is equal to 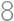 .
. ,
,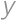 , and
, and 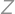 ?
?
Show / hide solution
Problem 10J
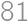 trees grow on a
trees grow on a 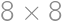 square grid. The gardener cut out one of the corner trees and is now standing at that corner facing the rest of the grid. However, he does not see some of the trees because they are aligned with the other trees. (A tree
square grid. The gardener cut out one of the corner trees and is now standing at that corner facing the rest of the grid. However, he does not see some of the trees because they are aligned with the other trees. (A tree 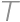 is aligned with another tree if there exists a tree on the line segment between the gardener and
is aligned with another tree if there exists a tree on the line segment between the gardener and 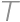 .)
.)
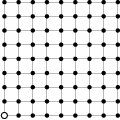
Show / hide solution
Problem 11J / 1S
How many ways are there to color the faces of a cube with two colors? Two colorings are considered identical if we can get one from the other by rotating the cube.
Show / hide answerShow / hide solution
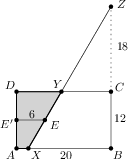
Problem 12J / 2S
A rectangle 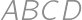 is given with
is given with 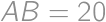 and
and 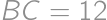 .
.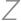 be the point on the ray
be the point on the ray 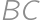 such that
such that 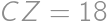 and
and 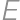 the point inside
the point inside 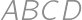 such that the distance from
such that the distance from 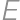 to both
to both 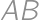 and
and 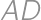 is
is 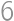 .
.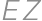 intersect
intersect 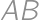 and
and 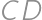 at points
at points 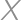 and
and 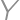 ,
,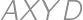 .
.
Show / hide solution
Problem 13J / 3S
For how many positive integers 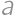 (
( ) is
) is 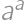 a square of a positive integer?
a square of a positive integer?
Show / hide solution
Problem 14J / 4S
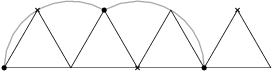
An equilateral triangle with side length 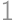 is lying on the floor, with one altitude perpendicular to the floor. We color one of its vertices red and we ”roll” the triangle on the floor (in the plane of the triangle) through one full rotation. What is the length of the red vertex's trajectory?
is lying on the floor, with one altitude perpendicular to the floor. We color one of its vertices red and we ”roll” the triangle on the floor (in the plane of the triangle) through one full rotation. What is the length of the red vertex's trajectory?
Show / hide solution
Problem 15J / 5S
What is the smallest positive integer consisting only of the digits 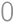 and
and 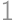 that is divisible by
that is divisible by 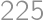 ?
?
Show / hide solution
Problem 16J / 6S
Bill is old enough to vote but not old enough to use the senior discount. (His age is between 18 and 70.) It is known that 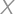 years ago, the square of his age was the same as his current age increased by
years ago, the square of his age was the same as his current age increased by 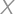 .
.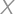 .
.
Show / hide solution
Problem 17J / 7S
Let us fold the bottom left corner of a rectangular paper to its top right corner. The resulting figure consists of three triangles created by the edges of the paper and the fold. For what ratio of side lengths of the paper is the ratio of the areas of the triangles 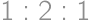 ?
?
Show / hide solution
Problem 18J / 8S
How many three digit numbers are divisible by 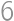 if each digit is larger than
if each digit is larger than 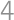 ?
?
Show / hide solution
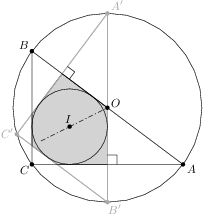
Problem 19J / 9S
Three circles with radius 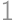 are given, such that each two are externally tangent. We put all the circles into a greater circle
are given, such that each two are externally tangent. We put all the circles into a greater circle 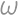 .
. .
.
Show / hide solution
Problem 20J / 10S
Let 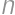 be a positive integer. If
be a positive integer. If 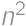 has
has 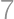 in the tens place, which digits can be in the units place?
in the tens place, which digits can be in the units place?
Show / hide solution
Problem 21J / 11S
If we write the numbers 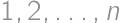 in some order, we will get an
in some order, we will get an 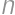 -chain.
-chain.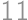 -chain
-chain
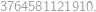
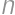 with
with 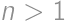 such that there exists an
such that there exists an 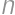 -chain
-chainShow / hide solution
Problem 22J / 12S
Find all triples 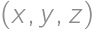 of positive real numbers for which
of positive real numbers for which 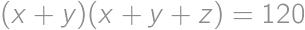 ,
,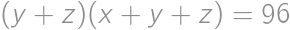 ,
, 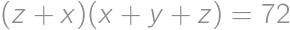 .
.
Show / hide solution
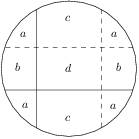
Problem 23J / 13S
A circle is given with a radius 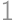 and two perpendicular chords inside it, dividing the circle into
and two perpendicular chords inside it, dividing the circle into 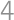 parts. We color the part with the greatest and the part with the smallest area in black and leave the rest white. We know that the area of the white parts is the same as the area of the black parts. What is the maximum possible distance of the longer chord to the centre?
parts. We color the part with the greatest and the part with the smallest area in black and leave the rest white. We know that the area of the white parts is the same as the area of the black parts. What is the maximum possible distance of the longer chord to the centre?
Show / hide solution
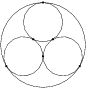
Problem 24J / 14S
An officer's route consists of three circles (shown in the picture). He must start at 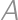 and travel the entire route, without visiting any portion twice except perhaps the intersection points, and return to
and travel the entire route, without visiting any portion twice except perhaps the intersection points, and return to 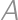 .
.
Show / hide solution
Problem 25J / 15S
A trapezoid has bases of lengths 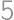 and
and 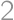 and legs of lengths
and legs of lengths 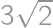 and
and 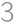 .
.
Show / hide solution
Problem 26J / 16S
There are 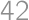 people in a row. They want to order themselves according to their height, so that the tallest one will stand in front. In one step, two people who are next to each other can switch position. At most, how many steps are necessary for them to order as they want?
people in a row. They want to order themselves according to their height, so that the tallest one will stand in front. In one step, two people who are next to each other can switch position. At most, how many steps are necessary for them to order as they want?
Show / hide solution
Problem 27J / 17S
Parsley lives in Vegetable State where one can pay only by coins with values  and
and 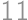 .
.
Show / hide solution
Problem 28J / 18S
Let us divide a circle with radius 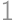 into
into 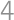 parts. What is the smallest possible perimeter of the part with the greatest area? If there is more than one part with the greatest area, we take into account the one with the smallest perimeter.
parts. What is the smallest possible perimeter of the part with the greatest area? If there is more than one part with the greatest area, we take into account the one with the smallest perimeter.
Show / hide solution
Problem 29J / 19S
Find the sum of all real numbers 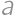 for which the equations
for which the equations 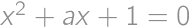 and
and 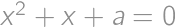 have at least one common real root.
have at least one common real root.
Show / hide solution
Problem 30J / 20S
How many 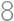 -digit
-digit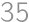 times smaller than the original one?
times smaller than the original one?
Show / hide solution
Problem 31J / 21S
Consider a right triangle with sides of integer length. One of the sides has length 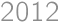 .
.
Show / hide solution
Problem 32J / 22S
Let 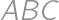 be a triangle with circumcentre
be a triangle with circumcentre  and orthocentre
and orthocentre  in the Cartesian plane. No two of these five points coincide and all of them have integer coordinates. What is the second smallest possible radius of a circle circumscribed around triangle
in the Cartesian plane. No two of these five points coincide and all of them have integer coordinates. What is the second smallest possible radius of a circle circumscribed around triangle 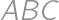 ?
?
Show / hide solution
Problem 33J / 23S
Find the largest positive integer 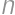 such that the number
such that the number 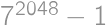 is divisible by
is divisible by 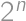 .
.
Show / hide solution
Problem 34J / 24S
If we calculate the product of the digits of some number, the product of the digits of the product, and so on, we arrive after a finite number of steps at a one digit number. The number of required steps is called the \textit*{persistence} of the number. For example, the number 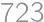 has persistence
has persistence 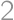 because
because 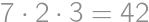 then
then 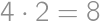 .
.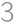 .
.
Show / hide solution
Problem 35J / 25S
If we extend the sides 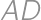 and
and 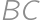 of a convex quadrilateral, they intersect at a point
of a convex quadrilateral, they intersect at a point 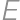 .
. and
and 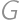 the midpoints of
the midpoints of 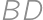 and
and 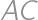 ,
,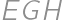 and the area of a quadrilateral
and the area of a quadrilateral 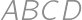 .
.
Show / hide solution
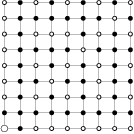
Problem 36J / 26S
Cube termites bore four straight square tunnels of sidelength 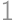 in each direction inside a cube (as you can see on the picture) and now they have left the cube. How many cm
in each direction inside a cube (as you can see on the picture) and now they have left the cube. How many cm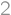 of paint do we need to cover the surface of what is left of the cube if the original cube had side length
of paint do we need to cover the surface of what is left of the cube if the original cube had side length 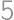 cm?
cm?
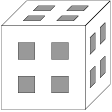
Show / hide solution
Problem 37J / 27S
We are given a circle with radius  .
.
Show / hide solution
Problem 38J / 28S
What is the greatest divisor of  that gives a remainder of
that gives a remainder of  when divided by
when divided by  ?
?
Show / hide solution
Problem 39J / 29S
A cube and 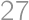 of its points are given: the vertices, midpoints of the edges, centers of the faces, and the center of the cube. How many lines are passing through exactly three of the given points?
of its points are given: the vertices, midpoints of the edges, centers of the faces, and the center of the cube. How many lines are passing through exactly three of the given points?
Show / hide solution
Problem 40J / 30S
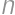 participants took part in a competition that lasted for
participants took part in a competition that lasted for 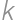 days. Each day each participant received an integer amount of points between
days. Each day each participant received an integer amount of points between 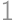 and
and 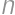 ,
,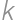 -th
-th points (when all the points for the whole competition were added). Find the sum of all
points (when all the points for the whole competition were added). Find the sum of all 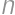 for which this is possible (regardless of
for which this is possible (regardless of 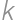 ).
).
Show / hide solution
Problem 41J / 31S
We want to cut a cylindrical cake with 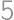 straight cuts. What is the maximum number of resulting pieces? For example, by
straight cuts. What is the maximum number of resulting pieces? For example, by 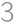 cuts we can divide the cake into
cuts we can divide the cake into 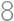 pieces.
pieces.
Show / hide solution
Problem 42J / 32S
An eight-branched star (Stella octangula) is a solid, which results from sticking eight regular tetrahedrons to the faces of an octahedron. All the edges of each tetrahedron and the octahedron have length 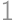 .
.
Show / hide solution
Problem 43J / 33S
A hitchhiker is walking along the road. The probability that a car picks him up in the next 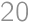 minutes is
minutes is 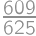 .
.
Show / hide solution
Problem 44J / 34S
A vandal and a moderator are editing a Wikipedia article. At the beginning, the article was without a mistake and each day the vandal adds one mistake. At the end of each day the moderator has 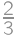 chance of having found each single mistake that is in the article. What is the probability that after three days the article will be without a mistake?
chance of having found each single mistake that is in the article. What is the probability that after three days the article will be without a mistake?
Show / hide solution
Problem 45J / 35S
We have a large enough heap of red, blue, and yellow cards. We can receive the following number of points:
- for each red card one point,
- for each blue card twice the number of red cards as points,
- for each yellow card three times the number of blue cards as points.
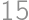 cards?
Show / hide answer
cards?
Show / hide answerShow / hide solution
Problem 46J / 36S
Matthew has one 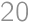 -sided
-sided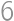 -sided
-sided
Show / hide solution
Problem 47J / 37S
Let us have a 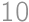 by
by 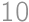 board. The rows and columns are numbered from left to right and top to bottom, respectively, by integers from
board. The rows and columns are numbered from left to right and top to bottom, respectively, by integers from 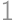 to
to 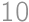 .
.
Show / hide solution
Problem 48J / 38S
We have a triangle with altitudes of sizes 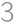 ,
,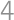 , and
, and 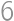 .
.
Show / hide solution
Problem 49J / 39S
Find the greatest integer 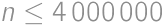 for which
for which  is rational.
is rational.
Show / hide solution
Problem 50J / 40S
A 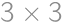 Maxi-square is a square divided into nine square tiles. Each tile is divided into four little squares in which the numbers
Maxi-square is a square divided into nine square tiles. Each tile is divided into four little squares in which the numbers 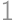 ,
,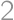 ,
, 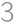 ,
,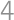 are written (each of them exactly once). Two tiles can touch only if their adjacent numbers match (as in dominoes). How many Maxi-squares exist?
are written (each of them exactly once). Two tiles can touch only if their adjacent numbers match (as in dominoes). How many Maxi-squares exist?
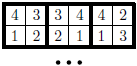
Show / hide solution
Problem 51J / 41S
Andrew calls his favourite number \textit*{balloon}. It holds for balloon that
- the sum of its digits is twice the number of its digits
- it does not have more than
 digits
digits - its digits are in turn even and odd (it doesn't have to start with an even digit)
- the number greater by one is divisible by
 .
.
Show / hide solution
Problem 52J / 42S
Find all four-digit positive integers  such that the last four digits of the number
such that the last four digits of the number 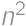 is the number
is the number 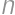 .
.
Show / hide solution
Problem 53J / 43S
Find the sum of all five-digit palindromes.
Show / hide answerShow / hide solution
Problem 54J / 44S
How many ordered quadruples of odd positive integers 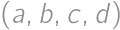 satisfy
satisfy 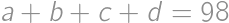 ?
?
Show / hide solution
Problem 55J / 45S
Find the only eleven-digit number such that
- it starts with a one
- when it it is written twice in a row, it is a perfect square.
Show / hide solution
Problem 56J / 46S
Two different triangles with side lengths 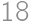 ,
,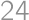 , and
, and 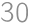 are given such that their incircles coincide and their circumcircles coincide. What is the area of the polygon that the triangles have in common?
are given such that their incircles coincide and their circumcircles coincide. What is the area of the polygon that the triangles have in common?
Show / hide solution
Problem 57J / 47S
In how many ways can we color the cells of a 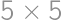 grid with black and white so that in each column and row there will be exactly two black squares?
grid with black and white so that in each column and row there will be exactly two black squares?
Show / hide solution
Problem 58J / 48S
Two distinct points 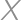 and
and 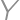 lie inside a square with side length
lie inside a square with side length 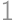 .
.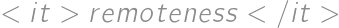 of a vertex of the square we mean its distance to the closer of the points
of a vertex of the square we mean its distance to the closer of the points  and
and  .
.
Show / hide solution
Problem 59J / 49S
The parking lot consists of  parking places regularly distributed in a row with numbers
parking places regularly distributed in a row with numbers  to
to  .
. cars park there one after each other, in the following way:
cars park there one after each other, in the following way:
- The first car chooses randomly one of the
 places.
places. - The following cars choose the place from which the distance to the closest car is the greatest (each of such places with the same probability).
 .
.Show / hide solution
Problem 60J / 50S
Find all real numbers 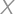 that satisfy
that satisfy
Show / hide solution
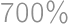
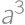 ,
,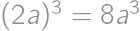 .
.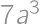 ,
,
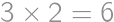
 .
.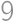 ,
,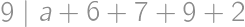 implying that
implying that  .
.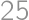 is sufficient.
is sufficient.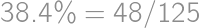
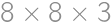 out of all pieces without chocolate. There must be then
out of all pieces without chocolate. There must be then 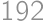 pieces of cake without chocolate on it. From the total amount of pieces with chocolate
pieces of cake without chocolate on it. From the total amount of pieces with chocolate 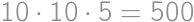 we easily count the desired percentage:
we easily count the desired percentage: 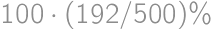 .
.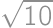
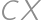 .
.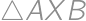 is right and isosceles we have
is right and isosceles we have 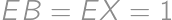 and the rest follows from the Pythagorean theorem.
and the rest follows from the Pythagorean theorem. 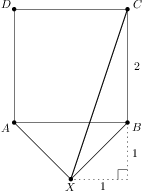
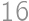 ways to vary the left-hand side and see if the right-hand side can be changed accordingly. The process can be speeded up by various observations (for instance the result has to start with 2, hence the first number is 4 and the second one starts with 5).
ways to vary the left-hand side and see if the right-hand side can be changed accordingly. The process can be speeded up by various observations (for instance the result has to start with 2, hence the first number is 4 and the second one starts with 5). .
.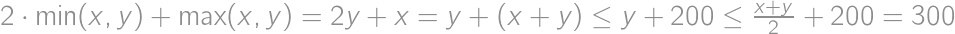 .
.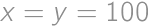 .
.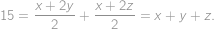
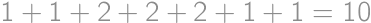
 .
.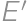 then
then 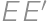 is the midline of the trapezoid
is the midline of the trapezoid 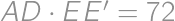 .
.
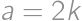 is even then
is even then 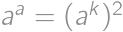 is always a square. If
is always a square. If 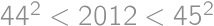 the answer is
the answer is 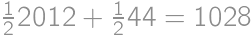 .
.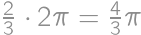
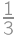 of a circumference of a circle with radius 1 and once it remains fixed. Hence the total length of its trajectory equals
of a circumference of a circle with radius 1 and once it remains fixed. Hence the total length of its trajectory equals 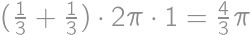 .
.
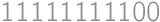
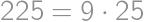 ), so the number of 1's is a multiple of nine. The smallest positive integer with these properties is
), so the number of 1's is a multiple of nine. The smallest positive integer with these properties is  and its square
and its square 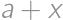 .
.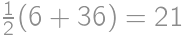 ,
,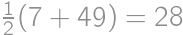 ,
, 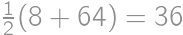 ,
,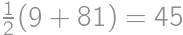 ,
, 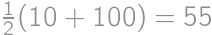 ,
,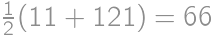 .
.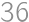 ,
,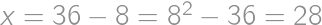 .
.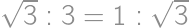 or in reverse order.
or in reverse order. 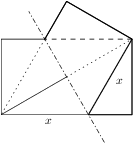
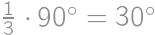 .
. ,
, (the order of the digits matters, so we have
(the order of the digits matters, so we have 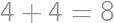 combinations). Similarly the remainder
combinations). Similarly the remainder 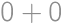 ,
,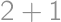 (again
(again 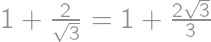
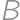 ,
, 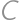 the centers of the smaller circles and by
the centers of the smaller circles and by 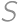 the center of
the center of 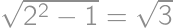 ,
,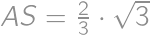 .
. and the radius of the smaller circle.
and the radius of the smaller circle. 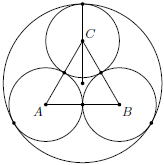
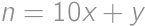 for an integer
for an integer 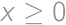 and a digit
and a digit 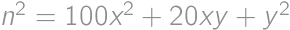 .
.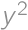 is odd. Therefore
is odd. Therefore 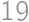 -chain:
-chain: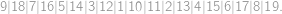
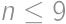 this condition cannot be satisfied. Similarly, for
this condition cannot be satisfied. Similarly, for 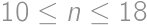 both digits
both digits 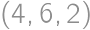
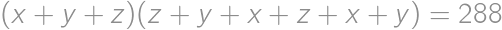 .
.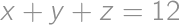 .
.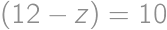 ,
,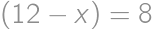 ,
, 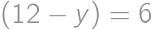 ,
,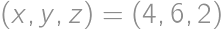 .
.
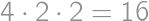 .
.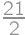
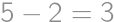 ,
,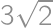 ,
,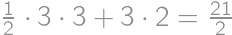 .
.
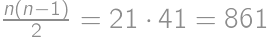
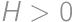 then there exists a step that decreases it. In the beginning,
then there exists a step that decreases it. In the beginning, 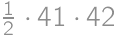 (if every pair is switched, i.e. if the people are in the opposite order). Thus, the ”worst” ordering requires
(if every pair is switched, i.e. if the people are in the opposite order). Thus, the ”worst” ordering requires 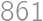 steps.
steps.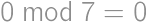 ,
, 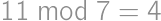 ,
,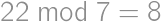 ,
, 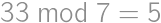 ,
,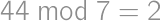 ,
, 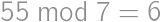 ,
,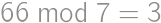 . From
. From 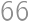 on, he can pay all the amounts, as the remainders repeat themselves. Thus, the last price he cannot pay is
on, he can pay all the amounts, as the remainders repeat themselves. Thus, the last price he cannot pay is 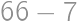 .
.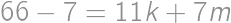 .
.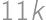 ) with remainder
) with remainder 
 .
.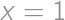 or
or  .
.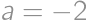 (substitute back). In the latter case the equations do not have any real roots.
(substitute back). In the latter case the equations do not have any real roots.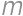 be a number that we get after crossing out the first digit and
be a number that we get after crossing out the first digit and 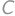 be the crossed out digit. The original number is then
be the crossed out digit. The original number is then 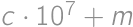 .
.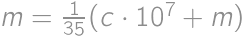 ,
,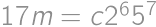 .
.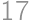 ,
,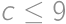 .
.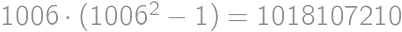
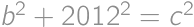 .
.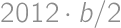 .
.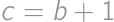 ,
,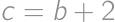 ,
, .
.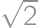 ,
, 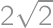 we see that the orthocentre coincides with one of the vertices. For
we see that the orthocentre coincides with one of the vertices. For 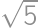 and
and 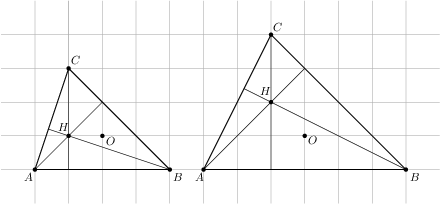
 several times to get
several times to get 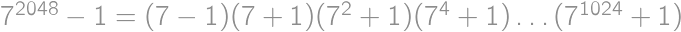 .
.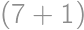 ,
,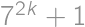 gives a remainder
gives a remainder 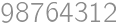
 ,
,
 merge into one point. Then
merge into one point. Then  is a midline in
is a midline in 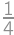 .
.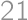 cm
cm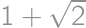
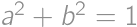 .
. ,
,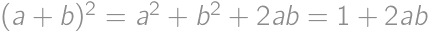 .
.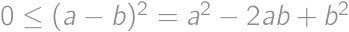 we have
we have 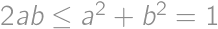 .
.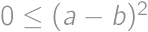 ,
,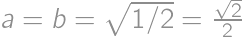 .
.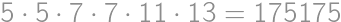
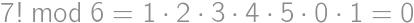 .
.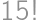 .
.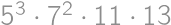 ,
,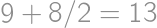 ), those that pass through the center of the side but not the center of the cube (
), those that pass through the center of the side but not the center of the cube (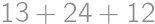 lines altogether.
lines altogether.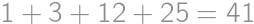
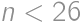 .
.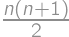 points allocated each day, that gives a total sum of
points allocated each day, that gives a total sum of 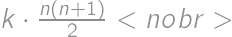 points. However, that is also equal to
points. However, that is also equal to 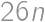 . Comparing these two expressions, we get
. Comparing these two expressions, we get 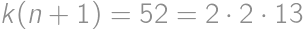 .
.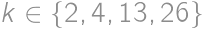 we can find a way in which the contestants could receive points during the competition and for
we can find a way in which the contestants could receive points during the competition and for 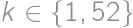 we cannot find such a way. The sum of all
we cannot find such a way. The sum of all 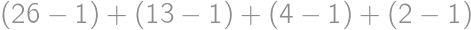 .
.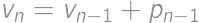 ,
,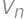 is the result for
is the result for 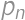 is the number of new parts, i.e. the number of parts into which we can divide a plane by lines. By drawing on paper we can find the maximum values for
is the number of new parts, i.e. the number of parts into which we can divide a plane by lines. By drawing on paper we can find the maximum values for 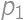 ,
,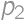 ,
, 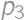 and
and 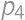 ,
,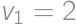 we get the result
we get the result 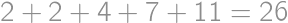 .
.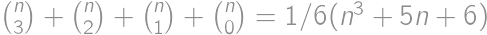 .
.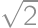
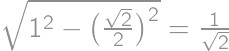 ,
,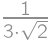 .
.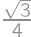 and the height
and the height 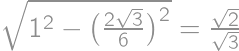 ,
,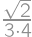 .
.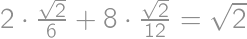 .
.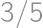
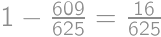 .
.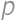 ,
,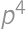 .
.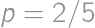 and the probability of catching a car is
and the probability of catching a car is 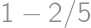 .
.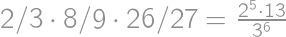
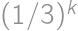 ,
,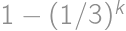 .
.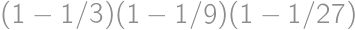 .
.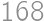
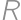 denote the number of red cards,
denote the number of red cards, 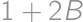 points to the overall score (
points to the overall score (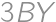 points. Therefore
points. Therefore 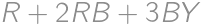 is the overall score. For
is the overall score. For 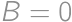 ,
,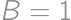 ,
,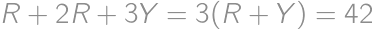 .
.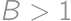 ,
,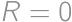 for
for 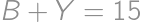 ,
,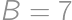 and
and 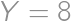 ,
,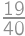
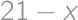 (from
(from 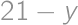 (from
(from 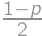 ,
,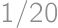 ,
,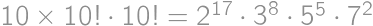
 ,
, except for
except for  will occur in the result exactly once. As for the
will occur in the result exactly once. As for the 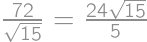
 ,
, a
a  and then compare this with the area
and then compare this with the area 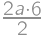 .
.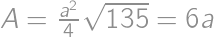 ,
,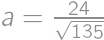 and perimeter is then
and perimeter is then 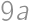 .
.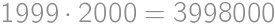
 ,
,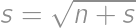 .
.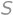 we get
we get 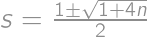 ,
,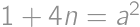 for some
for some 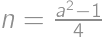 .
.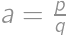 with
with 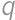 coprime, then
coprime, then 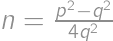 and
and 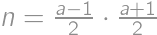 ,
,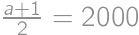 .
.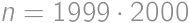 is the solution.
is the solution.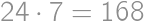
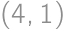 and
and 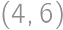 ,
,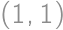 being the upper left corner square). Observe that
being the upper left corner square). Observe that 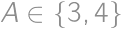 and
and 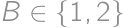 .
.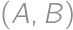 equals one of
equals one of 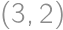 ,
,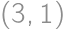 ,
,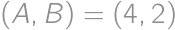 ,
,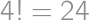 possible middle tiles, the result is
possible middle tiles, the result is 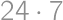 .
.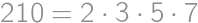 .
.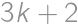 and also it should be twice the number of digits from the statement. So the digit sum is even, of the form
and also it should be twice the number of digits from the statement. So the digit sum is even, of the form 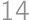 or
or 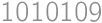 and
and 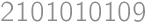 with digit sums
with digit sums 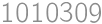 .
.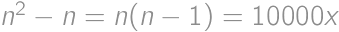 for some integer
for some integer 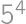 divides the right-hand side, it must divide the left-hand side; thus
divides the right-hand side, it must divide the left-hand side; thus 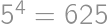 divides either
divides either 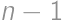 ,
,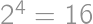 divides either
divides either 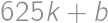 ,
,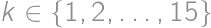 and
and 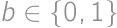 .
.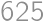 when divided by
when divided by 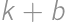 .
.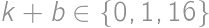 from the latter divisibility. It is then readily seen that
from the latter divisibility. It is then readily seen that 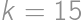 ,
,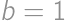 ,
, 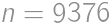 ;
;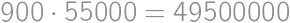 .
.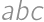 corresponds to the palindrome
corresponds to the palindrome 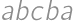 for a non-zero digit
for a non-zero digit 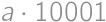 ,
,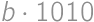 and each
and each 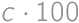 to the total sum. Each possible value of
to the total sum. Each possible value of 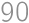 times. The total sum is thus
times. The total sum is thus 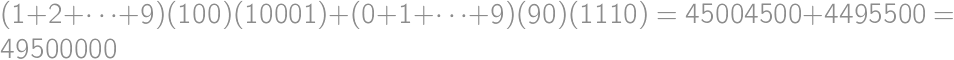 .
.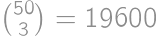
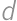 being odd. Let
being odd. Let 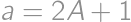 ,
,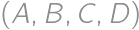 of nonnegative integers satisfying
of nonnegative integers satisfying 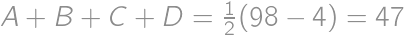 .
.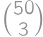 (each quadruple
(each quadruple 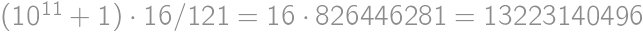
 created by subsequently writing
created by subsequently writing 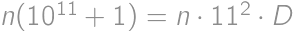 for a suitable integer
for a suitable integer 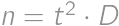 ,
,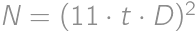 ,
,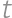 in such a way that
in such a way that 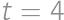 .
.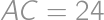 ,
, 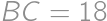 ).
).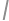 be the incenter of
be the incenter of 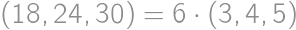 ,
, is right and the radii
is right and the radii  and
and 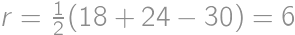 and
and 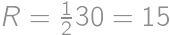 .
.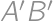 of the circle
of the circle 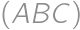 different from
different from  ;
;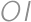 .
.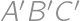 is then symmetrical to
is then symmetrical to 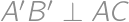 and
and 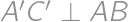 .
.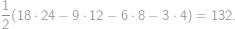
 (columns by letters). Without loss of generality, the cells
(columns by letters). Without loss of generality, the cells  ,
, are painted (from symmetry, it is sufficient to multiply the answer by
are painted (from symmetry, it is sufficient to multiply the answer by 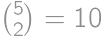 )
)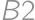 (multiply by four). If the cell
(multiply by four). If the cell 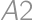 is painted, it remains to determine the number of complying paintings of
is painted, it remains to determine the number of complying paintings of 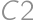 (multiply by 3), and in the third column
(multiply by 3), and in the third column 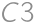 (again multiply by 3). If
(again multiply by 3). If 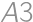 is now painted, there is only one possibility how to finish (
is now painted, there is only one possibility how to finish (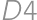 ,
, 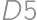 ,
,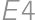 ,
, 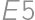 are painted). Otherwise there are four possibilities (without loss of generality in the third row
are painted). Otherwise there are four possibilities (without loss of generality in the third row 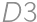 is painted and
is painted and 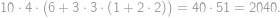
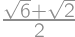
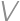 be the value we are minimizing. If
be the value we are minimizing. If 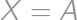 and
and  then
then 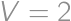 and using triangle inequalities it is easy to show that if
and using triangle inequalities it is easy to show that if 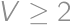 .
.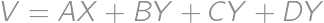 .
.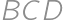 ,
,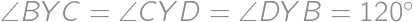 .
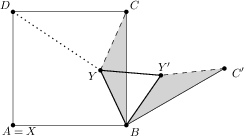
.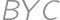 around
around 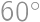 into a triangle
into a triangle 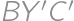 and comparing the length of the broken line
and comparing the length of the broken line 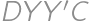 to the length of the segment
to the length of the segment 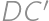 ).
).
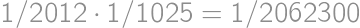
 )
) will be filled until gaps of size
will be filled until gaps of size  be the number of places which remain free, if the cars park on
be the number of places which remain free, if the cars park on 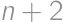 places in a row with first and last places already taken. The first car will park in the middle, which splits the task into the cases
places in a row with first and last places already taken. The first car will park in the middle, which splits the task into the cases 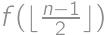 and
and 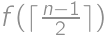 .
.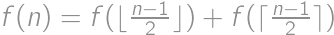 with initial conditions
with initial conditions 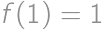 and
and 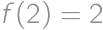 .
.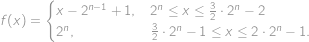
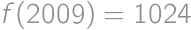 and the overall probability is
and the overall probability is 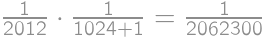 .
.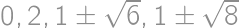

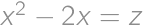 we get an equation
we get an equation 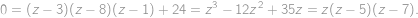
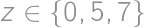 we can easily determine the corresponding
we can easily determine the corresponding 





















