Problem 1
Je známe, že číslo 2013 sa dá práve jedným spôsobom zapísať ako súčet dvoch prvočísel. Čomu je rovný ich súčin?
Show / hide answer
Show / hide solution
Aby bol súčet dvoch prirodzených čísel nepárny, musí byť jedno z nich nepárne a jedno párne. Jediným párnym prvočíslom je dvojka, takže v úvahu pripadá len zápis 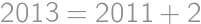 . Zadanie hovorí, že je možné zapísať 2013 ako súčet dvoch prvočísel, takže 2011 je prvočíslo a odpoveď je
. Zadanie hovorí, že je možné zapísať 2013 ako súčet dvoch prvočísel, takže 2011 je prvočíslo a odpoveď je 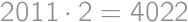 .
.
Problem 2
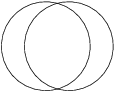
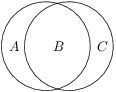
Dve kružnice s polomerom 1 sa pretínajú tak, že obsah prostrednej časti je rovný súčtu obsahov krajných dvoch. Čomu je rovný obsah prostrednej časti?
Show / hide answer
Show / hide solution
Označme obsahy troch častí ako na obrázku.
Zo symetrie vieme, že
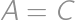 ,
, takže zo zadaného
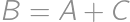
plynie
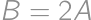 .
. Obsah prostrednej časti je tak rovný dvom tretinám obsahu ľavého kruhu, teda
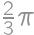 .
.
Problem 3
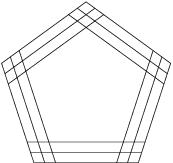
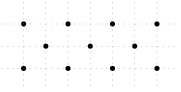
Máme päť žltých kolíkov, štyri červené, tri zelené, dva modré a jeden oranžový. Koľkými spôsobmi ich môžeme rozmiestniť do trojuholníkovej siete (pozri obrázok) tak, aby v žiadnom riadku ani stĺpci neboli dva kolíky rovnakej farby? Rovnako farebné kolíky považujeme za nerozlíšiteľné.
Show / hide answer
Show / hide solution
Začneme rozmiestňovaním žltých kolíkov. Máme jedinú možnosť, ako ich rozmiestniť tak, aby v každom riadku i stĺpci bol najviac jeden, a síce dať ho na preponu trojuholníka. Podobne máme iba jeden spôsob ako rozmiestniť postupne červené, zelené, modré a oranžové kolíky — vždy na preponu trojuholníka tvoreného doposiaľ neobsadenými miestami v trojuholníkovej sieti. Preto existuje iba jedno rozmiestnenie všetkých kolíkov vyhovujúce zadaniu.
Problem 4
Nájdite najmenšie prirodzené číslo, ktorého súčin cifier je rovný 600.
Show / hide answer
Show / hide solution
Pretože 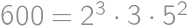 , môžeme na zostavenie tohto čísla použiť iba číslice 1, 2, 3, 4, 5, 6, 8. Pritom jednotky k súčinu nijak neprispejú, iba zväčšia počet cifier. Zrejme musí číslo obsahovať dve päťky, lebo
, môžeme na zostavenie tohto čísla použiť iba číslice 1, 2, 3, 4, 5, 6, 8. Pritom jednotky k súčinu nijak neprispejú, iba zväčšia počet cifier. Zrejme musí číslo obsahovať dve päťky, lebo 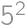 nemožno získať inou kombináciou cifier. Ostatné cifry musia mať súčin 24, teda musia byť aspoň dve. Číslo
nemožno získať inou kombináciou cifier. Ostatné cifry musia mať súčin 24, teda musia byť aspoň dve. Číslo 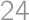 môžeme rozložiť ako
môžeme rozložiť ako 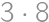 alebo
alebo  , a pretože prvá možnosť obsahuje menšiu číslicu, zvolíme ju a zostavíme hľadané číslo
, a pretože prvá možnosť obsahuje menšiu číslicu, zvolíme ju a zostavíme hľadané číslo 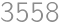 .
.
Problem 5
Kladné reálne čísla  ,
,  spĺňajú
spĺňajú
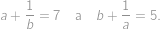
Čomu je rovná hodnota výrazu
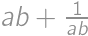 ?
Show / hide answer
Show / hide solution
?
Show / hide answer
Show / hide solution
Obe rovnosti medzi sebou vynásobíme a dostaneme
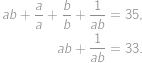
Problem 6
Lukáš objavil šesťciferné prirodzené číslo spĺňajúce nasledujúce podmienky:
- Číslo sa číta rovnako zľava doprava i sprava doľava.
- Je deliteľné deviatimi.
- Po škrtnutí prvej a poslednej cifry je jediným prvočíselným deliteľom nového čísla číslo 11.
Ktoré číslo Lukáš objavil?
Show / hide answer
Show / hide solution
Problem 7
Na priemere 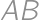 polkružnice
polkružnice  je daný bod
je daný bod 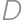 . Kolmica k
. Kolmica k 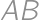 vedená bodom
vedená bodom 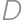 pretne polkružnicu
pretne polkružnicu  v bode
v bode 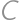 . Ak sú dĺžky oblúkov
. Ak sú dĺžky oblúkov 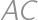 a
a 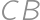 polkružnice
polkružnice  v pomere
v pomere 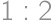 , určte hodnotu pomeru
, určte hodnotu pomeru 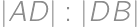 .
.
Show / hide answer
Show / hide solution
Problem 8
Dvaja rozmaznaní bratia Viktor a Mišo dostali balíček cukríkov, ktorý si pol na pol rozdelili. Každý z nich zje počas dňa dva až tri cukríky. Malému Viktorovi cukríky vydržali štrnásť dní, staršiemu Mišovi presne tri týždne. Koľko cukríkov bolo pôvodne v balíčku?
Show / hide answer
Show / hide solution
Problem 9
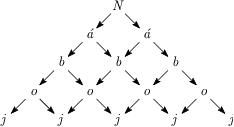
Koľkými spôsobmi môžeme v schéme na obrázku prečítať slovo Náboj?
Show / hide answer
Show / hide solution
Z každého z písmen N, á, b, o môžeme ďalej pokračovať v čítaní dvoma spôsobmi. Preto možno slovo Náboj prečítať celkom 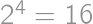 spôsobmi.
spôsobmi.
Problem 10
Na ostrove žijú obyvatelia dvoch typov: pravdovravní vždy hovoria pravdu, klamári zásadne klamú. Dvanásť obyvateľov ostrova sa posadilo do kruhu. Všetci svorne tvrdia, že sú pravdovravní. Tiež tvrdia, že po ich pravej ruke sedí klamár. Koľko najviac klamárov môže byť medzi týmito dvanástimi ľuďmi?
Show / hide answer
Show / hide solution
Predpokladajme, že by vedľa seba sedeli dvaja pravdovravní alebo dvaja klamári. Potom by ten, ktorý sedí v takej dvojici naľavo, prehlásil o človeku po svojej pravici, že je pravdovravný. To je ale v rozpore so zadaním — pravdovravní a klamári sa teda musia striedať. Klamárov je preto v kruhu práve šesť.
Problem 11
Lukáš má jedenásť zhodných štvorcových dlaždičiek — šesť červených, tri modré a dve zelené. Koľkými spôsobmi môže z niektorých deviatich z nich zostaviť tabuľku 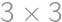 , ak musí ofarbenie tabuľky ostať zachované, ak ju otočíme o
, ak musí ofarbenie tabuľky ostať zachované, ak ju otočíme o 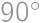 po smere hodinových ručičiek? Dlaždičky rovnakej farby považujeme za nerozlíšiteľné.
po smere hodinových ručičiek? Dlaždičky rovnakej farby považujeme za nerozlíšiteľné.
Show / hide answer
Show / hide solution
Aby zostalo ofarbenie pri otočení o 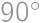 zachované, musia mať všetky rohové dlaždičky rovnakú farbu. Rovnakú farbu musia mať tiež štyri dlaždičky v stredoch krajných stĺpcov a riadkov. Potrebujeme preto buď aspoň osem dlaždičiek jednej farby, alebo po štyroch dlaždičkách z dvoch rôznych farieb. Také dlaždičky ale k dispozícii nemáme, a tak žiadne vyhovujúce ofarbenie neexistuje.
zachované, musia mať všetky rohové dlaždičky rovnakú farbu. Rovnakú farbu musia mať tiež štyri dlaždičky v stredoch krajných stĺpcov a riadkov. Potrebujeme preto buď aspoň osem dlaždičiek jednej farby, alebo po štyroch dlaždičkách z dvoch rôznych farieb. Také dlaždičky ale k dispozícii nemáme, a tak žiadne vyhovujúce ofarbenie neexistuje.
Problem 12
Na ostrove sú ženaté dve pätiny mužov a vydaté tri pätiny žien. Koľko percent obyvateľstva ostrova žije v manželstve?
Show / hide answer
Show / hide solution
Problem 13
Aká je dĺžka strany najväčšieho rovnostranného trojuholníka, ktorý možno vystrihnúť z obdĺžnikového papiera o rozmeroch 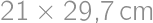 ?
?
Show / hide answer
Show / hide solution
Problem 14
Dáška si vzala štvorcový kus papiera a zložila ho štyrikrát na polovicu bez spätného rozkladania tak, že každým zložením vytvorila rovnoramenný pravouhlý trojuholník. Koľko štvorcov je vidieť po rozložení papiera?
Show / hide answer
Show / hide solution
Na nasledujúcom obrázku sú znázornené prehyby, ktoré uvidíme po rozložení papiera.
Uvidíme teda celkom desať štvorcov — celý papier, štvorec spájajúci stredy jeho strán a v každom z týchto štvorcov navyše štyri menšie.
Problem 15
Koľko päťuholníkov sa nachádza na obrázku?
Show / hide answer
Show / hide solution
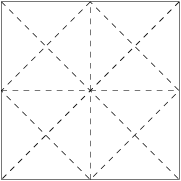
Všimneme si, že každý päťuholník musí mať vo svojom vnútri stred obrázku. Pre každú z piatich strán máme na výber z troch možností (vonkajšia, prostredná, vnútorná čiara), takže päťuholníkov na obrázku je 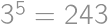 .
.
Problem 16
Pri sčítaní dvoch prirodzených čísel Pepa omylom za jedno z nich pripísal nulu, a tak mu vyšlo 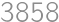 namiesto
namiesto 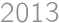 . Čomu je rovné väčšie z čísel, ktoré mal Pepa sčítať?
. Čomu je rovné väčšie z čísel, ktoré mal Pepa sčítať?
Show / hide answer
Show / hide solution
Označme  ,
,  čísla, ktoré mal Pepa sčítať. Keďže pripísanie nuly odpovedá vynásobeniu desiatimi, môžeme zostaviť rovnice
čísla, ktoré mal Pepa sčítať. Keďže pripísanie nuly odpovedá vynásobeniu desiatimi, môžeme zostaviť rovnice
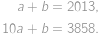
Ich odčítaním získame
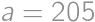 ,
, takže
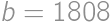 ,
, čo je hľadaný väčší sčítanec.
Problem 17
Aký polomer má najmenší kruh, ktorým možno zakryť trojuholník so stranami dĺžok 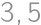 a
a 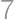 .
.
Show / hide answer
Show / hide solution
Problem 18
Lukáš, Mirek, Pepa a Viktor majú dokopy 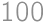 lízaniek. Pritom každý dvaja z nich majú dokopy lízaniek aspoň
lízaniek. Pritom každý dvaja z nich majú dokopy lízaniek aspoň 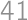 . Koľko najmenej lízaniek môže mať Pepa?
. Koľko najmenej lízaniek môže mať Pepa?
Show / hide answer
Show / hide solution
Problem 19
Viktor si nakreslil obdĺžnik 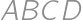 s obsahom
s obsahom 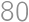 a dĺžkou uhlopriečky
a dĺžkou uhlopriečky 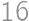 . Čomu je rovný sínus ostrého uhla, ktorý zvierajú uhlopriečky obdĺžnika?
. Čomu je rovný sínus ostrého uhla, ktorý zvierajú uhlopriečky obdĺžnika?
Show / hide answer
Show / hide solution
Problem 20
Akú najväčšiu hodnotu môže mať výraz 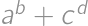 , ak
, ak  ,
,  ,
, 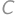 ,
, 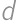 sú navzájom rôzne čísla z množiny
sú navzájom rôzne čísla z množiny 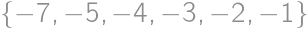 ?
?
Show / hide answer
Show / hide solution
Problem 21
Do roviny s kartézskou súradnicovou sústavou sme náhodne umiestnili uhol o veľkosti 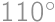 . Aká je pravdepodobnosť, že ramená tohto uhla tvoria graf funkcie?
. Aká je pravdepodobnosť, že ramená tohto uhla tvoria graf funkcie?
Show / hide answer
Show / hide solution
Problem 22
Pepa si v deň konania minuloročného náboja (23. marca 2012) nakreslil pravidelný stouholník 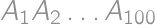 (číslovaný v smere hodinových ručičiek) a na jeden náhodný vrchol položil žetón. Každé ďalšie ráno potom posunul žetón o toľko vrcholov po smere hodinových ručičiek, aké bolo číslo vrcholu na ktorom práve žetón ležal (napríklad z vrcholu
(číslovaný v smere hodinových ručičiek) a na jeden náhodný vrchol položil žetón. Každé ďalšie ráno potom posunul žetón o toľko vrcholov po smere hodinových ručičiek, aké bolo číslo vrcholu na ktorom práve žetón ležal (napríklad z vrcholu 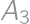 by sa tento žetón presunul na
by sa tento žetón presunul na 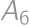 , z vrcholu
, z vrcholu 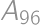 na
na 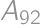 ). Teraz leží žetón na vrchole
). Teraz leží žetón na vrchole 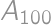 . Ak?? bola pravdepodobnosť, že sa niečo také stane?
. Ak?? bola pravdepodobnosť, že sa niečo také stane?
Show / hide answer
Show / hide solution
Problem 23
Prirodzeným číslam, ktoré sa dajú napísať ako rozdiel druhých mocnín dvoch celých čísel, hovorme rozdielové. Koľko z čísel  je rozdielových?
je rozdielových?
Show / hide answer
Show / hide solution
Problem 24
Tri pravidelné neprekrývajúce sa mnohouholníky o stranách dĺžky 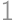 sa stretávajú v bode
sa stretávajú v bode 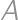 tak, že tvoria (nekonvexný) mnohouholník
tak, že tvoria (nekonvexný) mnohouholník 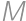 , pre ktorý je bod
, pre ktorý je bod 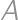 vnútorným bodom. Ak je jeden z mnohouholníkov šesťuholník a druhý štvorec, určte obvod mnohouholníka
vnútorným bodom. Ak je jeden z mnohouholníkov šesťuholník a druhý štvorec, určte obvod mnohouholníka 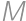 .
.
Show / hide answer
Show / hide solution
Porovnaním veľkostí vnútorných uhlov troch mnohouholníkov pri spoločnom vrchole 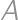 dostaneme, že veľkosť vnútorného uhla v treťom pravidelnom mnohouholníku je rovná
dostaneme, že veľkosť vnútorného uhla v treťom pravidelnom mnohouholníku je rovná 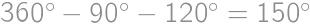 . Keďže súčet veľkostí vnútorných uhlov v
. Keďže súčet veľkostí vnútorných uhlov v 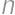 -uholníku je rovný
-uholníku je rovný 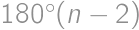 , platí:
, platí:
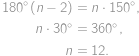
Tretí mnohouholník je teda dvanásťuholník a keďže každé dva mnohouholníky zdieľajú jednu stranu, má mnohouholník
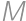
obvod rovný
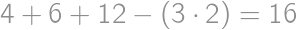 .
.
Problem 25
Viktor napísal na papier čísla 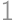 až
až 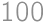 v náhodnom poradí. Aká je pravdepodobnosť, že pre každé
v náhodnom poradí. Aká je pravdepodobnosť, že pre každé 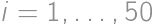 je to
je to 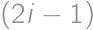 -te menšie ako to
-te menšie ako to 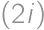 -te?
-te?
Show / hide answer
Show / hide solution
Predstavme si, že Viktor písal čísla postupne po dvojiciach — vždy si náhodne vybral dve doposiaľ nenapísané čísla a pripísal ich na papier za už napísané. Pravdepodobnosť, že napísal skôr to menšie, je 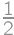 (bez ohľadu na to, ktoré dve čísla si vybral). Pre všetkých päťdesiat dvojíc teda máme pravdepodobnosť
(bez ohľadu na to, ktoré dve čísla si vybral). Pre všetkých päťdesiat dvojíc teda máme pravdepodobnosť 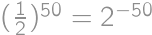 .
.
Problem 26
Ružová farba vznikne zmiešaním červenej a bielej v pomere 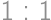 , azúrová vznikne z modrej a bielej v pomere
, azúrová vznikne z modrej a bielej v pomere 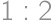 . Stanka si chce vymaľovať izbu farbou, ktorá vznikne z ružovej a azúrovej zmiešanej v pomere
. Stanka si chce vymaľovať izbu farbou, ktorá vznikne z ružovej a azúrovej zmiešanej v pomere 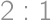 . Zatiaľ zmiešala tri plechovky modrej a jednu plechovku červenej farby. Ostávajú jej už len plechovky s červenou a bielou farbou. Koľko celkom plechoviek ešte musí pridať?
. Zatiaľ zmiešala tri plechovky modrej a jednu plechovku červenej farby. Ostávajú jej už len plechovky s červenou a bielou farbou. Koľko celkom plechoviek ešte musí pridať?
Show / hide answer
Show / hide solution
Problem 27
V klobúku je niekoľko bielych, sivých a čiernych králikov. Je známe, že keď kúzelník začne králiky postupne náhodne vyťahovať (bez toho, aby ich vracal späť), je pravdepodobnosť, že vytiahne skôr bieleho králika ako sivého, rovná 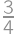 . Podobne je pravdepodobnosť, že vytiahne skôr sivého králika ako čierneho, rovná
. Podobne je pravdepodobnosť, že vytiahne skôr sivého králika ako čierneho, rovná 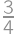 . Aká je pravdepodobnosť, že vytiahne skôr bieleho králika ako čierneho?
. Aká je pravdepodobnosť, že vytiahne skôr bieleho králika ako čierneho?
Show / hide answer
Show / hide solution
Pravdepodobnosť, že kúzelník vytiahne skôr bieleho králika ako sivého, je rovná 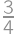 , takže v klobúku je trikrát viac bielych králikov ako sivých. Podobne je v klobúku trikrát viac sivých králikov ako čiernych. Z toho plynie, že bielych králikov je deväťkrát viac ako čiernych, a hľadaná pravdepodobnosť je tak rovná
, takže v klobúku je trikrát viac bielych králikov ako sivých. Podobne je v klobúku trikrát viac sivých králikov ako čiernych. Z toho plynie, že bielych králikov je deväťkrát viac ako čiernych, a hľadaná pravdepodobnosť je tak rovná 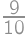 .
.
Problem 28
Pre prirodzené čísla  ,
,  platí
platí 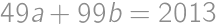 . Určte hodnotu súčtu
. Určte hodnotu súčtu  .
.
Show / hide answer
Show / hide solution
Problem 29
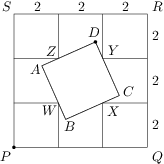
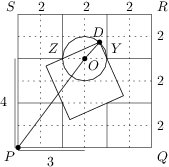
V rohoch štvorca 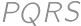 o strane dĺžky
o strane dĺžky 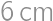 sú umiestnené štyri menšie štvorce o stranách dĺžky
sú umiestnené štyri menšie štvorce o stranách dĺžky 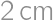 . Označme ich vrcholy
. Označme ich vrcholy 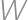 ,
, 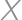 ,
, 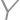 ,
, 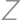 ako na obrázku. Štvorec
ako na obrázku. Štvorec 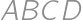 je zostrojený tak, že body
je zostrojený tak, že body 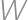 ,
, 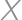 ,
, 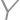 ,
, 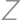 ležia vo vnútri jeho strán
ležia vo vnútri jeho strán 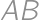 ,
, 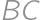 ,
, 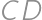 ,
, 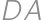 . Určte najväčšiu možnú vzdialenosť bodov
. Určte najväčšiu možnú vzdialenosť bodov 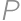 a
a 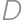 .
.
Show / hide answer
Show / hide solution
Problem 30
V dvadsiatich krabiciach je spolu 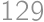 jabĺk. Pritom v niekoľkých krabiciach je presne po štyroch jablkách a v ostatných po
jabĺk. Pritom v niekoľkých krabiciach je presne po štyroch jablkách a v ostatných po 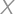 jablkách. Nájdite všetky možné hodnoty
jablkách. Nájdite všetky možné hodnoty 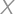 .
.
Show / hide answer
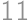 ,
, 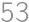
Problem 31
Kladné reálne čísla  ,
,  spĺňajú
spĺňajú  a súčasne
a súčasne
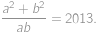
Čomu sa rovná hodnota výrazu
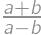 ?
Show / hide answer
Show / hide solution
?
Show / hide answer
Show / hide solution
Podmienku zo zadania si prepíšeme na 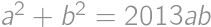 . Jej použitím dostávame nasledujúce vzťahy:
. Jej použitím dostávame nasledujúce vzťahy:
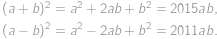
Keďže je hľadaný výraz kladný, môžeme jeho hodnotu spočítať pomocou vyššie uvedených rovností ako
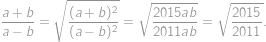
Problem 32
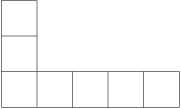
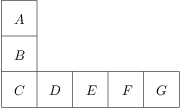
Koľkými spôsobmi možno do rôznych políčok heptomina na obrázku vyplniť čísla 1 až 7 (každé musíme použiť práve raz), aby bol súčet čísel v spodnom riadku rovnaký ako súčet čísel v ľavom stĺpci?
Show / hide answer
Show / hide solution
Problem 33
Dĺžky strán ostrouhlého trojuholníka 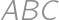 spĺňajú
spĺňajú 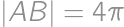 ,
, 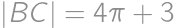 ,
, 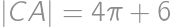 . Označme
. Označme 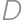 pätu výšky z vrcholu
pätu výšky z vrcholu 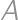 . Určte
. Určte 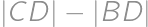 .
.
Show / hide answer
Show / hide solution
Pythagorova veta pre pravouhlé trojuholníky 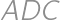 a
a 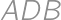 dáva
dáva 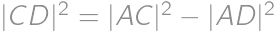 a
a 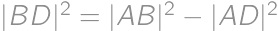 . Odčítaním týchto vzťahov dostaneme
. Odčítaním týchto vzťahov dostaneme
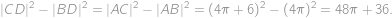
Keďže bod
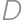
leží vo vnútri strany
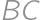 ,
, máme súčasne
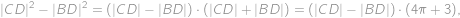
takže
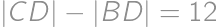 .
.
Problem 34
Električky majú celý deň v obidvoch smeroch trasy rovnaké intervaly. Chodec, ktorý šiel pozdĺž dráhy električky, pozoroval, že ho každých 12 minút jedna električka predbehne a zároveň každé 4 minúty ho minie električka v protismere. Aký interval majú električky?
Show / hide answer
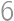 minút
minút
Označíme rýchlosť električky 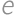 , rýchlosť chodca
, rýchlosť chodca 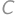 a vzdialenosť medzi električkami
a vzdialenosť medzi električkami 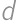 . Zadanie dáva
. Zadanie dáva
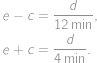
Spočítaním rovníc a vydelením dvoma dostávame
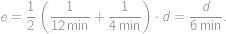
takže električka prejde vzdialenosť
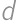
za 6 minút, čo odpovedá intervalu električky.
Problem 35
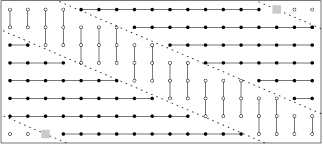
Koľko nedegenerovaných trojuholníkov môže byť vytvorených spojením niektorých troch bodov na obrázku?
Poznámka: Body sú zarovnané do naznačenej mriežky.
Show / hide answer
Show / hide solution
Počet spôsobov, ako vybrať niektoré tri body z dotyčných jedenástich, je rovný
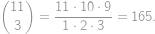
Ostáva spočítať, koľko trojíc bodov leží na priamke, a toto číslo odpočítať. Vodorovných trojíc je celkom
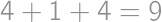 ,
, šikmých trojíc potom
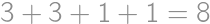 ,
, takže celkový počet trojuholníkov je
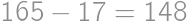 .
.
Problem 36
Mirek dostal bonboniéru s tridsiatimi bonbónmi usporiadanými v troch riadkoch po desať. Aby si ju náležite vychutnal, je bonbóny po jednom, a to tak, aby sa počty ostávajúcich bonbónov v každých dvoch riadkoch v každom okamihu líšili najviac o jedna. Koľkými spôsobmi môže bonboniéru zjesť?
Show / hide answer
Show / hide solution
Poradie, v akom Mirek bonbóny zje, môžeme jednoznačne zadať nasledovne: pre každý riadok určíme, v akom poradí budú bonbóny v tomto riadku zjedené; súčasne určíme, v akom poradí bude Mirek voliť riadky.
V každom riadku môžeme bonbóny usporiadať 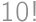 spôsobmi, vo všetkých troch riadkoch dohromady teda
spôsobmi, vo všetkých troch riadkoch dohromady teda 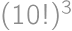 spôsobmi.
spôsobmi.
Pre určenie počtu možných poradí riadkov si uvedomme, že kedykoľvek je v každom riadku rovnaký počet bonbónov, potom si Mirek môže zvoliť ľubovoľný z nich. Pri ďalšom výbere si musí zvoliť jeden zo zostávajúcich dvoch (pri voľbe toho istého by v tomto už boli o dva bonbóny menej) a v následnom treťom výbere musí nutne zvoliť ten posledný nevybraný. Po troch zjedených bonbónoch teda bude vo všetkých riadkoch opäť rovnaký počet bonbónov. Stačí preto desaťkrát zvoliť poradie troch riadkov, čo je možné 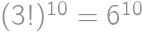 spôsobmi.
spôsobmi.
Možných spôsobov zjedenia bonboniéry je 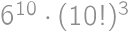 .
.
Problem 37
Povieme, že šesťciferné prirodzené číslo je dvojité, pokiaľ sa jeho prvé tri cifry (v tomto poradí) zhodujú s jeho ďalšími tromi ciframi (teda napríklad číslo 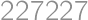 je dvojité, zatiaľ čo číslo
je dvojité, zatiaľ čo číslo 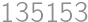 dvojité nie je). Koľko dvojitých čísel je bezo zvyšku deliteľných číslom
dvojité nie je). Koľko dvojitých čísel je bezo zvyšku deliteľných číslom 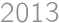 ?
?
Poznámka: Prirodzené číslo nemôže začínať nulou.
Show / hide answer
Show / hide solution
Problem 38
Na každé políčko hracieho plánu 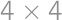 náhodne nakreslíme šípku doprava alebo dole a na ľavé horné políčko postavíme robota. Robot sa vždy posúva na susedné políčko v smere šípky. Aká je pravdepodobnosť, že robot opustí hrací plán krokom z pravého dolného políčka?
náhodne nakreslíme šípku doprava alebo dole a na ľavé horné políčko postavíme robota. Robot sa vždy posúva na susedné políčko v smere šípky. Aká je pravdepodobnosť, že robot opustí hrací plán krokom z pravého dolného políčka?
Show / hide answer
Show / hide solution
Spočítajme, koľkými rôznymi cestami sa robot môže do pravého dolného políčka dostať a aká je pravdepodobnosť priechodu jednej takej cesty. Každá cesta sa skladá z troch krokov dole a troch krokov doprava, čo dáva celkom 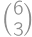 možných ciest. Pravdepodobnosť, že sa robot bude cesty držať, je v oboch prípadoch
možných ciest. Pravdepodobnosť, že sa robot bude cesty držať, je v oboch prípadoch 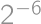 — každý zo šiestich krokov musí byť ten správny. Celková pravdepodobnosť je teda
— každý zo šiestich krokov musí byť ten správny. Celková pravdepodobnosť je teda 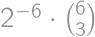 .
.
Problem 39
Vyjadrite
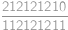
v základnom tvare (tj. ako zlomok
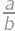 ,
, kde
 ,
, 
sú nesúdeliteľné prirodzené čísla).
Show / hide answer
Show / hide solution
Problem 40
Je daný obdĺžnik 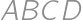 s dĺžkami strán
s dĺžkami strán 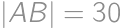 ,
, 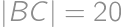 . Pre koľko bodov
. Pre koľko bodov  na jeho strane
na jeho strane 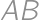 platí, že trojuholník
platí, že trojuholník 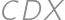 má celočíselný obvod?
má celočíselný obvod?
Show / hide answer
Show / hide solution
Problem 41
V akom poradí je potrebné usporiadať riadky 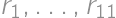 vyobrazenej tabuľky, aby vznikla tabuľka symetrická podľa vyznačenej uhlopriečky? Stačí nájsť jedno riešenie.
vyobrazenej tabuľky, aby vznikla tabuľka symetrická podľa vyznačenej uhlopriečky? Stačí nájsť jedno riešenie.
Show / hide answer
Show / hide solution
Všimnime si, že tabuľka je symetrická podľa opačnej uhlopriečky. K tomu, aby bola symetrická podľa vyznačenej uhlopriečky, ju stačí preklopiť podľa vodorovnej osi.
Poznámka: Pre túto tabuľku iné riešenie než uvedených 11 neexistuje.
Problem 42
Pre každé prirodzené číslo 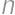 položme
položme
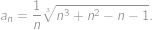
Nájdite najmenšie prirodzené číslo
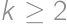
také, že
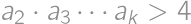 .
Show / hide answer
Show / hide solution
.
Show / hide answer
Show / hide solution
Označme 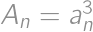 a ekvivalentne skúmajme, pre ktoré najmenšie prirodzené číslo
a ekvivalentne skúmajme, pre ktoré najmenšie prirodzené číslo 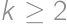 je
je 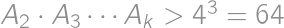 . Platí
. Platí
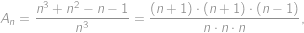
takže
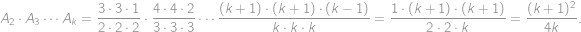
Teraz už ostáva len vyriešiť v prirodzených číslach nerovnicu
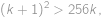
ktorá je po roznásobení ľavej strany a vydelení kladným

ekvivalentná s
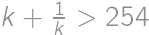
. Riešením je číslo 254.
Problem 43
Kaťa pripravila pizzu, rozkrájala ju na 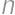 rovnakých dielikov a potom na ne pripichla lístky s číslami
rovnakých dielikov a potom na ne pripichla lístky s číslami 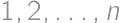 (každé číslo použila práve raz) tak, že medzi dielikmi so za sebou idúcimi číslami bol vždy rovnaký počet iných dielikov. Potom prišiel Lukáš a skoro celú pizzu zjedol — ostali len tri susedné dieliky s číslami 11, 4 a 17 (v tomto poradí). Koľko dielikov mala pizza pôvodne?
(každé číslo použila práve raz) tak, že medzi dielikmi so za sebou idúcimi číslami bol vždy rovnaký počet iných dielikov. Potom prišiel Lukáš a skoro celú pizzu zjedol — ostali len tri susedné dieliky s číslami 11, 4 a 17 (v tomto poradí). Koľko dielikov mala pizza pôvodne?
Show / hide answer
Show / hide solution
Nech medzi dielikmi so za sebou idúcimi číslami je práve 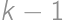 iných dielikov, teda „skokom“ o
iných dielikov, teda „skokom“ o  dielikov sa dostaneme z dieliku
dielikov sa dostaneme z dieliku 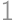 na dielik
na dielik 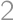 , z dieliku
, z dieliku 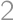 na dielik
na dielik 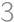 atď. Tieto skoky musia byť všetky v rovnakom smere, pretože prvým skokom v opačnom smere by sme sa dostali na predchádzajúci dielik s nižším číslom. Z dieliku
atď. Tieto skoky musia byť všetky v rovnakom smere, pretože prvým skokom v opačnom smere by sme sa dostali na predchádzajúci dielik s nižším číslom. Z dieliku 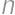 potom nutne skočíme na dielik
potom nutne skočíme na dielik 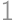 , pretože všetky ostatné majú vo vzdialenosti
, pretože všetky ostatné majú vo vzdialenosti  dielik s o jedna menším a o jedna väčším číslom.
dielik s o jedna menším a o jedna väčším číslom.
Pretože skákaním o  prejdeme postupne všetky dieliky pizze, existuje také
prejdeme postupne všetky dieliky pizze, existuje také 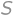 , že ak skočíme o
, že ak skočíme o  presne
presne 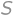 -krát, skončíme na susednom dieliku. Platí teda
-krát, skončíme na susednom dieliku. Platí teda
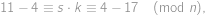
odkiaľ dostávame, že
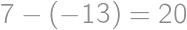
musí byť deliteľné
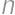 .
. Pretože však existuje dielik s číslom
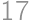 ,
, musí byť
 ,
, teda
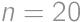 .
.
Problem 44
V jednej posluchárni na Matfyze sú miesta na sedenie usporiadané do obdĺžnikovej mriežky. Počas jednej prednášky z analýzy sedelo v každom rade presne 11 chlapcov, v každom stĺpci sedeli presne 3 dievčatá a ešte celkovo dve miesta zostali voľné. Koľko najmenej miest môže byť v posluchárni?
Show / hide answer
Show / hide solution
Označme 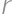 a
a 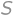 počet radov a stĺpcov v posluchárni. Zo zadania plynie
počet radov a stĺpcov v posluchárni. Zo zadania plynie 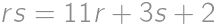 , čo upravíme na
, čo upravíme na
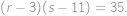
Buď sú teda zátvorky v nejakom poradí rovné 5 a 7 alebo 1 a 35. Vyskúšaním štyroch možností zistíme, že najmenšia hodnota súčinu
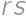
odpovedá prípadu
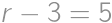 ,
, 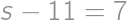
a je rovná
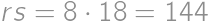 .
. Do takejto posluchárne možno študentov naozaj rozmiestniť — napríklad ako na obrázku.
Problem 45
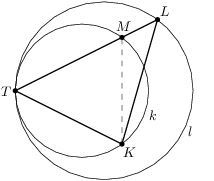
Kružnica  s polomerom 3 a kružnica
s polomerom 3 a kružnica 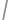 s polomerom 4 majú vnútorný dotyk v bode
s polomerom 4 majú vnútorný dotyk v bode 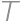 . Aký najväčší obsah môže mať trojuholník
. Aký najväčší obsah môže mať trojuholník 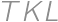 , ktorého vrcholy
, ktorého vrcholy 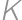 ,
, 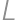 ležia po rade na kružniciach
ležia po rade na kružniciach  ,
, 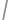 ?
?
Show / hide answer
Show / hide solution
Symbolom 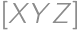 budeme označovať obsah trojuholníka
budeme označovať obsah trojuholníka 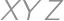 .
.
Označme
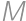
priesečník úsečky
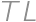
s kružnicou

rôzny od
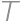 .
. Keďže
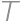
je stredom rovnoľahlosti s koeficientom
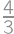
zobrazujúcim kružnicu

na kružnicu
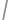 ,
, je bod
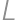
obrazom bodu
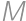 ,
, a teda
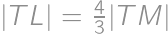
a
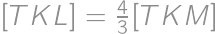
(trojuholníky zdieľajú výšku z vrcholu
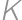 ).
). Stačí preto maximalizovať obsah trojuholníka
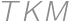
vpísaného do kružnice

s polomerom
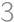 .
. Zo všetkých takýchto trojuholníkov má najväčší obsah ten rovnostranný, a to

Obsah príslušného trojuholníka
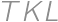
potom vyjde
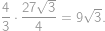
Problem 46
Lukáš a Viktor hrajú hru. Na začiatku majú množinu 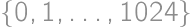 a striedajú sa v ťahoch. Najskôr Lukáš odoberie ľubovoľných jej
a striedajú sa v ťahoch. Najskôr Lukáš odoberie ľubovoľných jej 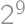 prvkov, potom odoberie Viktor ľubovoľných
prvkov, potom odoberie Viktor ľubovoľných 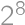 prvkov, potom Lukáš
prvkov, potom Lukáš 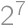 prvkov a tak ďalej až nakoniec odoberie Viktor jeden prvok, takže v množine presne dve čísla ostanú. Tým hra končí a Lukáš zaplatí Viktorovi absolútnu hodnotu rozdielu týchto čísel v eurách. Koľko eur Viktor vyhrá, pokiaľ obidvaja hráči hrajú najlep??ie ako môžu?
prvkov a tak ďalej až nakoniec odoberie Viktor jeden prvok, takže v množine presne dve čísla ostanú. Tým hra končí a Lukáš zaplatí Viktorovi absolútnu hodnotu rozdielu týchto čísel v eurách. Koľko eur Viktor vyhrá, pokiaľ obidvaja hráči hrajú najlep??ie ako môžu?
Show / hide answer
Show / hide solution
Viktor môže v každom svojom ťahu zdvojnásobiť najmenšiu vzdialenosť medzi dvomi číslami v množine tým, že z nich odoberie každý druhý prvok. Takto si zaistí výhru aspoň 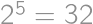 eur. Naopak Lukáš môže každým svojim ťahom znížiť rozdiel najväčšieho a najmenšieho čísla o polovicu tým, že odoberie spodnú alebo hornú časť množiny, a teda vie zaistiť, že Viktor vyhrá najviac
eur. Naopak Lukáš môže každým svojim ťahom znížiť rozdiel najväčšieho a najmenšieho čísla o polovicu tým, že odoberie spodnú alebo hornú časť množiny, a teda vie zaistiť, že Viktor vyhrá najviac 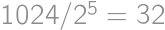 eur. Pri optimálnej hre obidvoch hráčov tak Viktor vyhrá 32 eur.
eur. Pri optimálnej hre obidvoch hráčov tak Viktor vyhrá 32 eur.
Problem 47
Na Matfyze vyhodili z analýzy niekoľko študentov. Všetci títo študenti prestúpili na VŠN (vysokú školu nemenovanú). To malo nasledujúce dôsledky:
- Počet študentov na Matfyze sa znížil o šestinu.
- Počet študentov na VŠN sa zvýšil o tretinu.
- Na obidvoch školách vzrástlo priemerné IQ o 2%.
Koľkokrát je teraz priemerné IQ na Matfyze vyššie ako na VŠN?
Show / hide answer
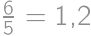 -krát
-krát
Problem 48
Do kružnice  s polomerom 1 je vpísaný pravidelný štrnásťuholník
s polomerom 1 je vpísaný pravidelný štrnásťuholník  . Aká je plocha tej časti kruhu ohraničeného kružnicou
. Aká je plocha tej časti kruhu ohraničeného kružnicou  , ktorá leží vo vnútri ostrého uhla
, ktorá leží vo vnútri ostrého uhla 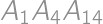 ?
?
Show / hide answer
Show / hide solution
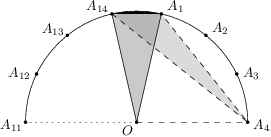
Zamerajme sa okrem bodov 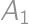 ,
, 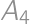 a
a 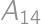 ešte na bod
ešte na bod 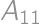 .
.
Keďže
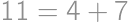 ,
, je úsečka
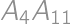
priemerom kružnice
 .
. Súčasne je
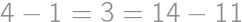 ,
, takže
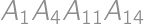
je rovnoramenný lichobežník a jeho základne
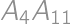
a
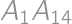
sú rovnobežné. Obsah trojuholníka
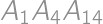
je preto rovnaký ako obsah trojuholníka
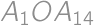 ,
, kde
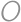
je stred kružnice
 .
. Hľadaný obsah je tak rovný obsahu kruhového výseku
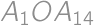 ,
, teda jednej štrnástine obsahu celého kruhu.
Problem 49
Olin s Martinou uvideli 24-prvkovú množinu  . Olin si vypísal všetky jej dvanásťprvkové podmnožiny, ktoré majú párny súčet prvkov, zato Martina si vypísala všetky dvanásťprvkové podmnožiny s nepárnym súčtom prvkov. Kto si vypísal viac množín a o koľko?
. Olin si vypísal všetky jej dvanásťprvkové podmnožiny, ktoré majú párny súčet prvkov, zato Martina si vypísala všetky dvanásťprvkové podmnožiny s nepárnym súčtom prvkov. Kto si vypísal viac množín a o koľko?
Show / hide answer
Olin o 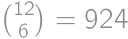
Uvažujme ľubovoľnú dvanásťprvkovú podmnožinu 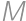 a predpokladajme, že existuje prirodzené číslo
a predpokladajme, že existuje prirodzené číslo 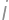 také, že
také, že 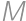 obsahuje práve jedno z čísel
obsahuje práve jedno z čísel 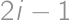 ,
, 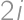 . Vezmeme najmenšie také
. Vezmeme najmenšie také 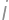 a zostrojme dvanásťprvkovú množinu
a zostrojme dvanásťprvkovú množinu 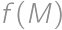 , ktorá bude obsahovať rovnaké prvky ako
, ktorá bude obsahovať rovnaké prvky ako 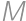 až na to, že z dvojice
až na to, že z dvojice 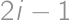 ,
, 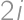 bude obsahovať ten druhý prvok.
bude obsahovať ten druhý prvok.
Ľahko si rozmyslíme, že keď 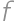 prevedieme na jednu množinu dvakrát po sebe, získame opäť pôvodnú množinu, a ďalej, že ak prevedieme
prevedieme na jednu množinu dvakrát po sebe, získame opäť pôvodnú množinu, a ďalej, že ak prevedieme 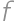 na niektorú Olinovu podmnožinu, získame Martininu podmnožinu a obrátene. Funkcia
na niektorú Olinovu podmnožinu, získame Martininu podmnožinu a obrátene. Funkcia 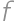 je teda bijekciou medzi Olinovými a Martininými podmnožinami, samozrejme iba tými, pre ktoré existuje
je teda bijekciou medzi Olinovými a Martininými podmnožinami, samozrejme iba tými, pre ktoré existuje 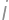 z predchádzajúceho odseku. Ostáva si rozmyslieť, ako vyzerajú „zvyšné“ množiny, pre ktoré také
z predchádzajúceho odseku. Ostáva si rozmyslieť, ako vyzerajú „zvyšné“ množiny, pre ktoré také 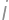 nie je možné nájsť.
nie je možné nájsť.
V takýchto podmnožinách musí byť práve šesť nepárnych čísel a šesť párnych čísel, ktoré sú následníkmi tých nepárnych. Súčet čísel v takýchto podmnožinách je tak vždy párny a ich počet je 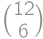 .
.
Problem 50
Viktor si myslí tri navzájom rôzne prirodzené čísla  ,
,  ,
, 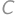 také, že súčet niektorých dvoch z nich je 800. Keď si na papier napísal čísla
také, že súčet niektorých dvoch z nich je 800. Keď si na papier napísal čísla  ,
,  ,
, 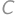 ,
, 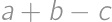 ,
, 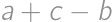 ,
, 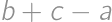 a
a 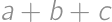 , zistil, že to sú všetko prvočísla. Určte rozdiel najväčšieho a najmenšieho čísla na Viktorovom papieri.
, zistil, že to sú všetko prvočísla. Určte rozdiel najväčšieho a najmenšieho čísla na Viktorovom papieri.
Show / hide answer
Show / hide solution
Bez ujmy na všeobecnosti predpokladajme, že 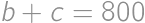 . Aspoň jedno z čísel
. Aspoň jedno z čísel  ,
, 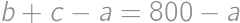 ,
, 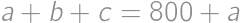 je deliteľné tromi, takže aby bolo súčasne prvočíslom, musí sa trom priamo rovnať. Keďže
je deliteľné tromi, takže aby bolo súčasne prvočíslom, musí sa trom priamo rovnať. Keďže 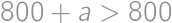 , ponúkajú sa dve možnosti:
, ponúkajú sa dve možnosti:  alebo
alebo 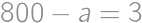 .
.
Pokiaľ  , máme z Viktorových prvočísel
, máme z Viktorových prvočísel 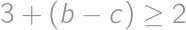 a súčasne
a súčasne 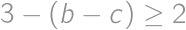 , teda
, teda 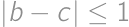 , čo vzhľadom k
, čo vzhľadom k 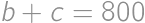 nepripadá do úvahy.
nepripadá do úvahy.
Vieme teda, že 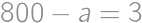 , čiže
, čiže 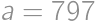 . Najväčšie z Viktorových čísel je
. Najväčšie z Viktorových čísel je 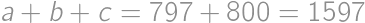 . Vzhľadom k predpokladu
. Vzhľadom k predpokladu 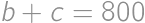 nemôže byť žiadne z Viktorových prvočísel párne, a preto je najmenšie číslo
nemôže byť žiadne z Viktorových prvočísel párne, a preto je najmenšie číslo 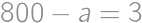 . Rozdiel tak je
. Rozdiel tak je 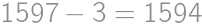 .
.
Ešte poznamenajme, že čísla vyhovujúce zadaniu skutočne existujú — napríklad 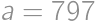 ,
, 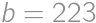 ,
, 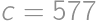 .
.
Problem 51
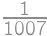
Alča na dve náhodné miesta metrovej tyčky nakreslila bodky. Potom prišiel Pepa a tyčku náhodne rozlámal na 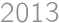 častí. Aká je pravdepodobnosť, že obe bodky sú teraz na tej istej časti?
častí. Aká je pravdepodobnosť, že obe bodky sú teraz na tej istej časti?
Show / hide answer
Show / hide solution
Predstavme si tyčku v celku. Alča na ňu náhodne naniesla dve bodky, ale Pepa na ňu náhodne naniesol 2012 zlomov. Celkom je tak na tyčke 2014 značiek, z toho dve náhodné značky sú bodky. Celkový počet možností, ktoré značky môžu byť bodky, je 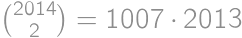 . Bodky sú na jednom dieliku presne vtedy, keď ide o susedné značky, na čo máme
. Bodky sú na jednom dieliku presne vtedy, keď ide o susedné značky, na čo máme 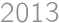 možností. Výsledná pravdepodobnosť je
možností. Výsledná pravdepodobnosť je
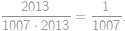
Problem 52
Koľko desaťciferných prirodzených čísel obsahujúcich každú z cifier 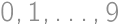 práve raz je násobkom čísla
práve raz je násobkom čísla 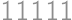 ?
?
Poznámka: Prirodzené číslo nemôže začínať nulou.
Show / hide answer
Show / hide solution
Pretože 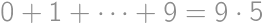 , musia byť skúmané čísla deliteľné deviatimi, teda dokonca číslom
, musia byť skúmané čísla deliteľné deviatimi, teda dokonca číslom 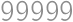 . Označme
. Označme 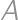 , resp.
, resp. 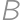 , číslo zložené z prvej, resp. druhej, pätice cifier skúmaného čísla. Potom máme
, číslo zložené z prvej, resp. druhej, pätice cifier skúmaného čísla. Potom máme
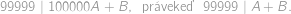
Pretože sú
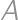 ,
, 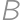
päťciferné prirodzené čísla menšie ako 99999, je
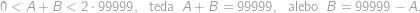
Z toho dostávame nutnú a postačujúcu podmienku na
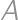 ,
, 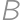
pre deliteľnosť príslušného desaťciferného čísla číslom
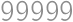 :
: Pre
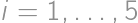
je
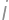 -tá
-tá cifra čísla
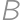
doplnkom do deviatky
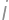 -tej
-tej cifry čísla
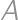 .
. Ponúkané cifry preto spárujeme do piatich dvojíc
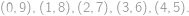
Vieme, že tieto dvojice musíme použiť v istom poradí (
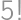
možností), a súčasne si pri každej dvojici môžeme vybrať, ktoré číslo z dvojice dáme do
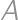
a ktoré do
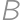
(
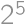
možností). Musíme však odčítať možnosti obsahujúce nulu na začiatku
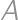 ,
, pre ktoré nedostaneme desaťciferné číslo — to je
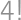
možností ako usporiadať ostatné dvojice, a
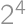
možností ako rozdeliť ich čísla medzi
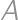
a
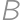 .
. Celkový počet čísel spĺňajúcich zadanie je teda
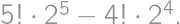
Problem 53
Polynóm 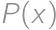 stupňa
stupňa 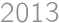 s reálnymi koeficientmi spĺňa pre
s reálnymi koeficientmi spĺňa pre 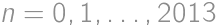 vzťah
vzťah 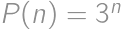 . Určte
. Určte 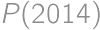 .
.
Show / hide answer
Show / hide solution
Definujme polynóm 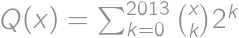 . Ten má stupeň 2013 a tiež pre ľubovoľné
. Ten má stupeň 2013 a tiež pre ľubovoľné 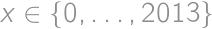 spĺňa podľa binomickej vety
spĺňa podľa binomickej vety
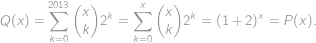
Polynóm
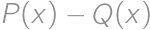
je stupňa 2013 a má 2014 koreňov, teda je nulový. Teda
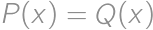 .
. Ostáva spočítať
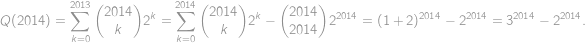
Problem 54
Vo vnútri rovnoramenného trojuholníka 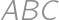 spĺňajúceho
spĺňajúceho 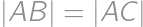 a
a 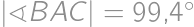 je daný bod
je daný bod 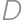 tak, že
tak, že 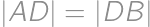 a
a 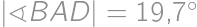 . Určte
. Určte 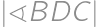 .
.
Show / hide answer
Show / hide solution
Označme 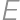 obraz bodu
obraz bodu 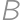 v osovej súmernosti podľa
v osovej súmernosti podľa 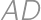 .
.
Potom
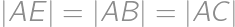
a
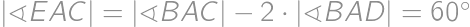 ,
, takže trojuholník
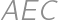
je rovnostranný a
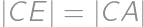 .
. Vďaka osovej súmernosti však tiež
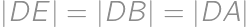 ,
, takže
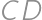
je os úsečky
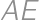
a
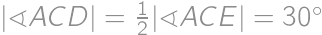 .
. Teraz už z nekonvexného štvoruholníka
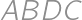
ľahko dopočítame
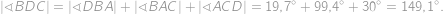
Problem 55
Nájdite najväčšie prirodzené číslo nekončiace nulou také, že škrtnutím niektorej jeho „vnútornej“ cifry získame jeho deliteľa.
Poznámka: „Vnútornou“ cifrou rozumieme každú cifru okrem prvej a poslednej.
Show / hide answer
Show / hide solution
Označme hľadané číslo 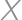 . Najskôr si rozmyslíme, že škrtať musíme jeho druhú cifru.
. Najskôr si rozmyslíme, že škrtať musíme jeho druhú cifru.
Pre spor predpokladajme, že prvé dve cifry neboli škrtnuté. Škrtnutím sme dostali z 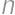 -ciferného čísla
-ciferného čísla 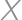 číslo
číslo 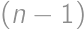 -ciferné (nazvime ho
-ciferné (nazvime ho 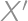 ). Potom
). Potom 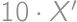 je opäť
je opäť 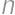 -ciferné číslo, ktoré sa s
-ciferné číslo, ktoré sa s 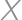 zhoduje v prvých dvoch cifrách, ale pritom sa mu nerovná, pretože pôvodné číslo nekončilo nulou. To je ale spor, lebo dva násobky
zhoduje v prvých dvoch cifrách, ale pritom sa mu nerovná, pretože pôvodné číslo nekončilo nulou. To je ale spor, lebo dva násobky 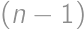 -ciferného čísla sa nemôžu líšiť o
-ciferného čísla sa nemôžu líšiť o 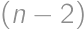 -ciferné číslo.
-ciferné číslo.
Číslo 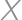 si teraz zapíšeme v tvare
si teraz zapíšeme v tvare 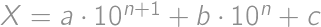 , kde
, kde  a
a  sú cifry (
sú cifry (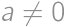 ) a
) a 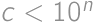 číslo nekončiace na nulu. Škrtnutím druhej cifry vznikne číslo
číslo nekončiace na nulu. Škrtnutím druhej cifry vznikne číslo 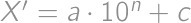 . Pre vhodné
. Pre vhodné 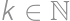 tak musí platiť
tak musí platiť
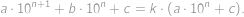
Uvedomme si, že  . Skutočne, keby bolo
. Skutočne, keby bolo  , začínalo by
, začínalo by 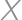 na väčšiu cifru ako
na väčšiu cifru ako 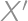 , čo nemôže. Upravme ďalej rovnosť do tvaru
, čo nemôže. Upravme ďalej rovnosť do tvaru
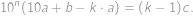
Keďže ľavá strana je deliteľná
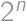
i
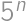 ,
, musí byť obidvoma deliteľná i pravá strana. Číslo
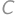
samozrejme nekončí na nulu, takže činiteľ
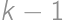
musí byť deliteľný aspoň jedným z prvočísel
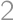 ,
, 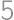
v jeho plnej mocnine. Keďže
 ,
, usudzujeme, že
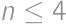
(lebo
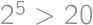 ,
, a dokonca
 ),
), a teda
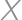
je najviac šesťciferné. Naopak pre

musí byť už nutne
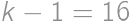 ,
, čo po dosadení dáva
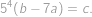
Aby vyšla pravá strana nezáporná, musí byť

(

a

sú cifry). Pre

máme možnosti
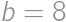 ,
, 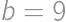
, z ktorých druhú zavrhujeme, lebo
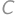
by končilo na nulu. Pre
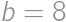
dopočítame
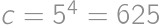 ,
, spätne dosadíme a overíme, že číslo
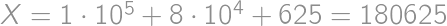
úlohu skutočne rieši.
Problem 56
Pre navzájom rôzne reálne čísla  ,
,  ,
, 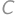 platí
platí
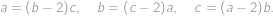
Čomu je rovný súčin
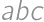 ?
Show / hide answer
Show / hide solution
?
Show / hide answer
Show / hide solution
Pokiaľ je jedno z čísel  ,
,  ,
, 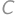 nulové, potom sú nulové všetky, čo je v spore s tým, že sú navzájom rôzne. Podobne zistíme, že čísla
nulové, potom sú nulové všetky, čo je v spore s tým, že sú navzájom rôzne. Podobne zistíme, že čísla  ,
,  ,
, 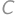 sú rôzne od troch.
sú rôzne od troch.
Dosaďme tretí vzťah do prvých dvoch a druhý vzťah 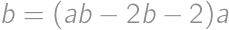 upravme na
upravme na 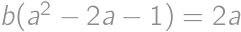 . Keďže pravá strana je nenulová, je nenulová i ľavá — môžeme teda deliť výrazom
. Keďže pravá strana je nenulová, je nenulová i ľavá — môžeme teda deliť výrazom 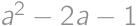 a tým získať vyjadrenie
a tým získať vyjadrenie  pomocou
pomocou  . To dosadíme do prvého vzťahu. Po úprave dostaneme
. To dosadíme do prvého vzťahu. Po úprave dostaneme
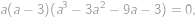
takže

je koreňom polynómu
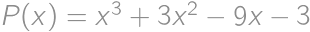 .
. Analogicky odvodíme, že i

a
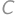
sú korene tohto polynómu. Keďže sú čísla
 ,
, 
,
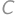
navzájom rôzne, znamená to, že
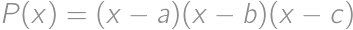 .
. Porovnaním koeficientov u absolútneho člena získavame hľadané
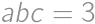 .
.
Problem 57
V rôznostrannom trojuholníku 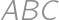 má jedna výška rovnakú dĺžku ako jedna ťažnica a iná výška má rovnakú dĺžku ako iná ťažnica. V akom pomere sú dĺžka tretej výšky a dĺžka tretej ťažnice?
má jedna výška rovnakú dĺžku ako jedna ťažnica a iná výška má rovnakú dĺžku ako iná ťažnica. V akom pomere sú dĺžka tretej výšky a dĺžka tretej ťažnice?
Show / hide answer
Show / hide solution
Bez ujmy na všeobecnosti predpokladajme, že 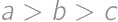 . Potom pre dĺžky príslušných výšok a ťažníc platí
. Potom pre dĺžky príslušných výšok a ťažníc platí 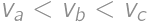 a
a 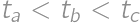 . Súčasne
. Súčasne  ,
,  a
a  , takže musí byť
, takže musí byť 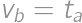 a
a 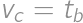 . Označme
. Označme 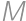 stred strany
stred strany 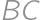 a
a 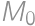 pätu kolmice z bodu
pätu kolmice z bodu 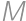 na stranu
na stranu 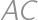 . V pravouhlom trojuholníku
. V pravouhlom trojuholníku 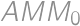 platí
platí 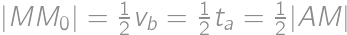 , takže
, takže 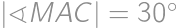 . Ak označíme
. Ak označíme 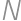 stred strany
stred strany 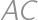 , získame podobne
, získame podobne 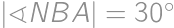 .
.
Označme 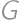 ťažisko trojuholníka
ťažisko trojuholníka 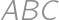 a uvažujme rovnostranný trojuholník
a uvažujme rovnostranný trojuholník 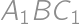 , ktorý má
, ktorý má 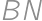 za ťažnicu. Bod
za ťažnicu. Bod 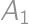 spĺňa
spĺňa 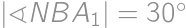 i
i 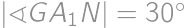 , ale pritom sa líši od bodu
, ale pritom sa líši od bodu 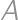 (trojuholník
(trojuholník 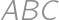 musí byť zo zadania rôznostranný). „Pravý“ bod
musí byť zo zadania rôznostranný). „Pravý“ bod 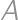 je preto druhým priesečníkom polpriamky
je preto druhým priesečníkom polpriamky 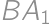 a kružnicového oblúka
a kružnicového oblúka 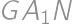 , teda stredom úsečky
, teda stredom úsečky 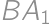 . Z toho plynie
. Z toho plynie 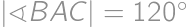 a
a 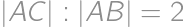 .
.
V trojuholníku s uhlom 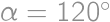 a dĺžkami strán
a dĺžkami strán 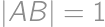 ,
, 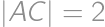 už ľahko z kosínusovej vety dopočítame dĺžku strany
už ľahko z kosínusovej vety dopočítame dĺžku strany  a dĺžku ťažnice
a dĺžku ťažnice 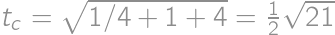 , ďalej obsah
, ďalej obsah  a nakoniec dĺžku výšky
a nakoniec dĺžku výšky 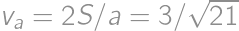 . Celkovo tak dostávame
. Celkovo tak dostávame
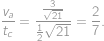

 ,
, spĺňajú
spĺňajú 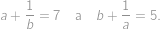
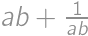 ?
?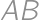 polkružnice
polkružnice  je daný bod
je daný bod  .
.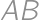 vedená bodom
vedená bodom  pretne polkružnicu
pretne polkružnicu  v bode
v bode 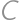 .
.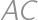 a
a 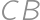 polkružnice
polkružnice  v pomere
v pomere 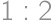 ,
,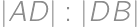 .
.
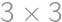 ,
,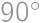 po smere hodinových ručičiek? Dlaždičky rovnakej farby považujeme za nerozlíšiteľné.
po smere hodinových ručičiek? Dlaždičky rovnakej farby považujeme za nerozlíšiteľné. ?
?
 namiesto
namiesto  .
.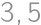 a
a 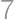 .
.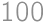 lízaniek. Pritom každý dvaja z nich majú dokopy lízaniek aspoň
lízaniek. Pritom každý dvaja z nich majú dokopy lízaniek aspoň 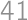 .
.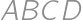 s obsahom
s obsahom 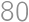 a dĺžkou uhlopriečky
a dĺžkou uhlopriečky 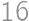 .
.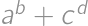 ,
, ,
, ,
, 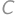 ,
,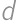 sú navzájom rôzne čísla z množiny
sú navzájom rôzne čísla z množiny 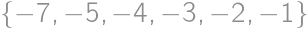 ?
?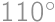 .
.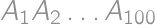 (číslovaný v smere hodinových ručičiek) a na jeden náhodný vrchol položil žetón. Každé ďalšie ráno potom posunul žetón o toľko vrcholov po smere hodinových ručičiek, aké bolo číslo vrcholu na ktorom práve žetón ležal (napríklad z vrcholu
(číslovaný v smere hodinových ručičiek) a na jeden náhodný vrchol položil žetón. Každé ďalšie ráno potom posunul žetón o toľko vrcholov po smere hodinových ručičiek, aké bolo číslo vrcholu na ktorom práve žetón ležal (napríklad z vrcholu 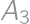 by sa tento žetón presunul na
by sa tento žetón presunul na 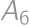 ,
,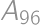 na
na  ).
). .
. je rozdielových?
je rozdielových? sa stretávajú v bode
sa stretávajú v bode 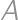 tak, že tvoria (nekonvexný) mnohouholník
tak, že tvoria (nekonvexný) mnohouholník  ,
, vnútorným bodom. Ak je jeden z mnohouholníkov šesťuholník a druhý štvorec, určte obvod mnohouholníka
vnútorným bodom. Ak je jeden z mnohouholníkov šesťuholník a druhý štvorec, určte obvod mnohouholníka  .
.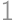 až
až 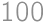 v náhodnom poradí. Aká je pravdepodobnosť, že pre každé
v náhodnom poradí. Aká je pravdepodobnosť, že pre každé 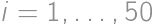 je to
je to 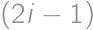 -te
-te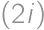 -te?
-te? ,
, .
. .
. .
.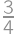 .
. ,
, platí
platí 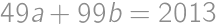 .
. .
.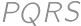 o strane dĺžky
o strane dĺžky 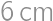 sú umiestnené štyri menšie štvorce o stranách dĺžky
sú umiestnené štyri menšie štvorce o stranách dĺžky 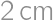 .
.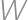 ,
,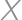 ,
, 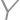 ,
,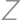 ako na obrázku. Štvorec
ako na obrázku. Štvorec 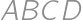 je zostrojený tak, že body
je zostrojený tak, že body 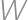 ,
,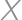 ,
, 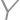 ,
,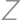 ležia vo vnútri jeho strán
ležia vo vnútri jeho strán 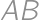 ,
,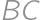 ,
, 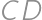 ,
,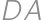 . Určte najväčšiu možnú vzdialenosť bodov
. Určte najväčšiu možnú vzdialenosť bodov 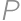 a
a 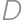 .
.
 jabĺk. Pritom v niekoľkých krabiciach je presne po štyroch jablkách a v ostatných po
jabĺk. Pritom v niekoľkých krabiciach je presne po štyroch jablkách a v ostatných po 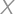 jablkách. Nájdite všetky možné hodnoty
jablkách. Nájdite všetky možné hodnoty 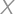 .
. ,
, spĺňajú
spĺňajú  a súčasne
a súčasne 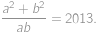
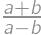 ?
?
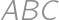 spĺňajú
spĺňajú 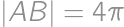 ,
,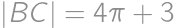 ,
, 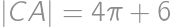 .
. pätu výšky z vrcholu
pätu výšky z vrcholu 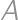 .
.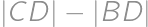 .
.
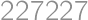 je dvojité, zatiaľ čo číslo
je dvojité, zatiaľ čo číslo 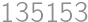 dvojité nie je). Koľko dvojitých čísel je bezo zvyšku deliteľných číslom
dvojité nie je). Koľko dvojitých čísel je bezo zvyšku deliteľných číslom 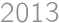 ?
?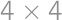 náhodne nakreslíme šípku doprava alebo dole a na ľavé horné políčko postavíme robota. Robot sa vždy posúva na susedné políčko v smere šípky. Aká je pravdepodobnosť, že robot opustí hrací plán krokom z pravého dolného políčka?
náhodne nakreslíme šípku doprava alebo dole a na ľavé horné políčko postavíme robota. Robot sa vždy posúva na susedné políčko v smere šípky. Aká je pravdepodobnosť, že robot opustí hrací plán krokom z pravého dolného políčka?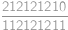
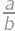 ,
, ,
, sú nesúdeliteľné prirodzené čísla).
Show / hide answer
sú nesúdeliteľné prirodzené čísla).
Show / hide answer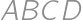 s dĺžkami strán
s dĺžkami strán 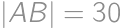 ,
,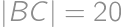 . Pre koľko bodov
. Pre koľko bodov 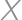 na jeho strane
na jeho strane 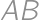 platí, že trojuholník
platí, že trojuholník 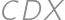 má celočíselný obvod?
má celočíselný obvod?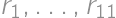 vyobrazenej tabuľky, aby vznikla tabuľka symetrická podľa vyznačenej uhlopriečky? Stačí nájsť jedno riešenie.
vyobrazenej tabuľky, aby vznikla tabuľka symetrická podľa vyznačenej uhlopriečky? Stačí nájsť jedno riešenie. 
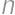 položme
položme 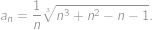
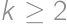 také, že
také, že 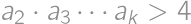 .
. rovnakých dielikov a potom na ne pripichla lístky s číslami
rovnakých dielikov a potom na ne pripichla lístky s číslami 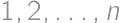 (každé číslo použila práve raz) tak, že medzi dielikmi so za sebou idúcimi číslami bol vždy rovnaký počet iných dielikov. Potom prišiel Lukáš a skoro celú pizzu zjedol — ostali len tri susedné dieliky s číslami 11, 4 a 17 (v tomto poradí). Koľko dielikov mala pizza pôvodne?
(každé číslo použila práve raz) tak, že medzi dielikmi so za sebou idúcimi číslami bol vždy rovnaký počet iných dielikov. Potom prišiel Lukáš a skoro celú pizzu zjedol — ostali len tri susedné dieliky s číslami 11, 4 a 17 (v tomto poradí). Koľko dielikov mala pizza pôvodne? s polomerom 3 a kružnica
s polomerom 3 a kružnica 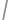 s polomerom 4 majú vnútorný dotyk v bode
s polomerom 4 majú vnútorný dotyk v bode 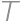 .
. ,
, ,
, ležia po rade na kružniciach
ležia po rade na kružniciach  ,
, ?
?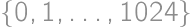 a striedajú sa v ťahoch. Najskôr Lukáš odoberie ľubovoľných jej
a striedajú sa v ťahoch. Najskôr Lukáš odoberie ľubovoľných jej 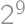 prvkov, potom odoberie Viktor ľubovoľných
prvkov, potom odoberie Viktor ľubovoľných 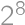 prvkov, potom Lukáš
prvkov, potom Lukáš 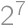 prvkov a tak ďalej až nakoniec odoberie Viktor jeden prvok, takže v množine presne dve čísla ostanú. Tým hra končí a Lukáš zaplatí Viktorovi absolútnu hodnotu rozdielu týchto čísel v eurách. Koľko eur Viktor vyhrá, pokiaľ obidvaja hráči hrajú najlep??ie ako môžu?
prvkov a tak ďalej až nakoniec odoberie Viktor jeden prvok, takže v množine presne dve čísla ostanú. Tým hra končí a Lukáš zaplatí Viktorovi absolútnu hodnotu rozdielu týchto čísel v eurách. Koľko eur Viktor vyhrá, pokiaľ obidvaja hráči hrajú najlep??ie ako môžu? s polomerom 1 je vpísaný pravidelný štrnásťuholník
s polomerom 1 je vpísaný pravidelný štrnásťuholník  .
. ,
,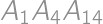 ?
? .
. ,
, ,
, 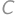 také, že súčet niektorých dvoch z nich je 800. Keď si na papier napísal čísla
také, že súčet niektorých dvoch z nich je 800. Keď si na papier napísal čísla  ,
, ,
, 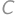 ,
,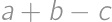 ,
, 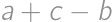 ,
,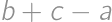 a
a 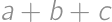 ,
,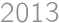 častí. Aká je pravdepodobnosť, že obe bodky sú teraz na tej istej časti?
častí. Aká je pravdepodobnosť, že obe bodky sú teraz na tej istej časti? práve raz je násobkom čísla
práve raz je násobkom čísla 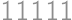 ?
?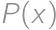 stupňa
stupňa 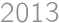 s reálnymi koeficientmi spĺňa pre
s reálnymi koeficientmi spĺňa pre 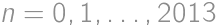 vzťah
vzťah 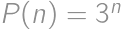 .
.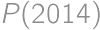 .
. spĺňajúceho
spĺňajúceho 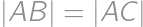 a
a 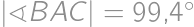 je daný bod
je daný bod 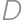 tak, že
tak, že 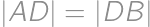 a
a 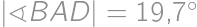 .
.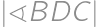 .
. ,
, ,
, 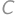 platí
platí 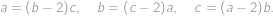
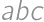 ?
?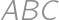 má jedna výška rovnakú dĺžku ako jedna ťažnica a iná výška má rovnakú dĺžku ako iná ťažnica. V akom pomere sú dĺžka tretej výšky a dĺžka tretej ťažnice?
má jedna výška rovnakú dĺžku ako jedna ťažnica a iná výška má rovnakú dĺžku ako iná ťažnica. V akom pomere sú dĺžka tretej výšky a dĺžka tretej ťažnice?
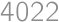
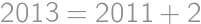 .
.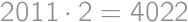 .
.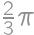
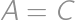 ,
,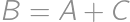 plynie
plynie 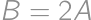 .
.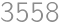
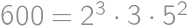 ,
,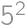 nemožno získať inou kombináciou cifier. Ostatné cifry musia mať súčin 24, teda musia byť aspoň dve. Číslo
nemožno získať inou kombináciou cifier. Ostatné cifry musia mať súčin 24, teda musia byť aspoň dve. Číslo 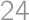 môžeme rozložiť ako
môžeme rozložiť ako 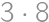 alebo
alebo  ,
,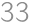
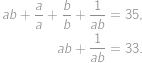
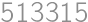
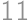 ,
,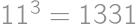 .
.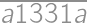 ,
,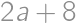 deliteľný deviatimi. Tento výraz je párny a menší ako
deliteľný deviatimi. Tento výraz je párny a menší ako 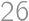 ,
,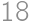 .
. a nami hľadané číslo je
a nami hľadané číslo je 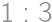
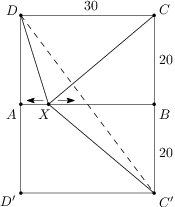
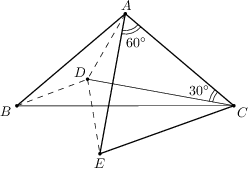
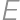 tak, aby body
tak, aby body 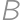 (v tomto poradí) tvorili štyri po sebe idúce vrcholy pravidelného šesťuholníka.
(v tomto poradí) tvorili štyri po sebe idúce vrcholy pravidelného šesťuholníka. 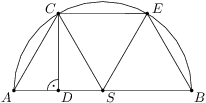
 stred polkružnice
stred polkružnice 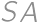 ,
,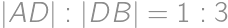 .
.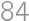
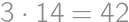 cukríkov, zatiaľ čo Mišo ich zjedol minimálne
cukríkov, zatiaľ čo Mišo ich zjedol minimálne 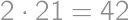 .
.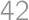 cukríkov. V balíčku pôvodne bolo
cukríkov. V balíčku pôvodne bolo 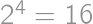 spôsobmi.
spôsobmi.
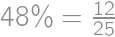
 ,
,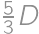 .
.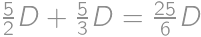 ľudí, z toho
ľudí, z toho 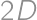 je zosobášených. Podiel ostrovanov žijúcich v manželstve je teda
je zosobášených. Podiel ostrovanov žijúcich v manželstve je teda 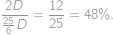
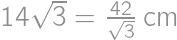
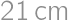 ,
,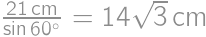 .
.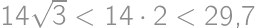 ,
,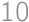
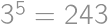
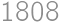
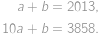
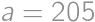 ,
,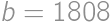 ,
,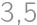
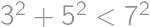 ,
,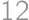
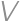 ,
,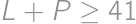 ,
,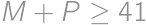 a
a 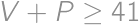 .
.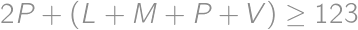 .
.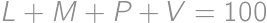 ,
,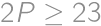 ,
, (
(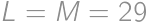 ,
,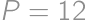 ,
, 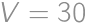 všetkým podmienkam úlohy vyhovujú, takže takáto možnosť môže nastať.
všetkým podmienkam úlohy vyhovujú, takže takáto možnosť môže nastať.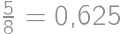
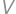 dĺžku výšky na stranu
dĺžku výšky na stranu 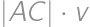 ,
,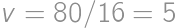 .
.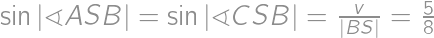 .
.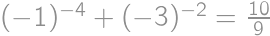
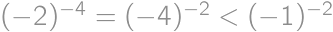 ,
, a
a  .
. a
a  .
.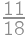
 .
.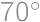 sa prvýkrát stane to, že každému bodu na osi
sa prvýkrát stane to, že každému bodu na osi 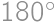 .
.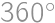 vyšetrovať nemusíme, lebo tu je situácia symetrická. Pravdepodobnosť, že sú ramená nášho uhla grafom nejakej funkcie, je teda
vyšetrovať nemusíme, lebo tu je situácia symetrická. Pravdepodobnosť, že sú ramená nášho uhla grafom nejakej funkcie, je teda 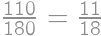 .
.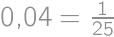
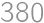 krát) vynásobíme dvojkou, budú deliteľné
krát) vynásobíme dvojkou, budú deliteľné 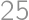 a naopak všetky čísla
a naopak všetky čísla 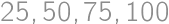 zrejme vyhovujú (už ich štvornásobky končia číslicami
zrejme vyhovujú (už ich štvornásobky končia číslicami 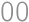 ).
).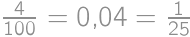 .
.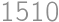
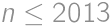 ,
,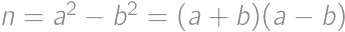 pre nejaké
pre nejaké 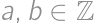 .
.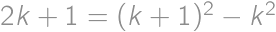 ,
,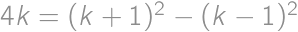 .
.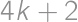 ,
,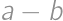 sú buď obe párne alebo obe nepárne (ich súčin je teda buď nepárny, alebo deliteľný štyrmi).
sú buď obe párne alebo obe nepárne (ich súčin je teda buď nepárny, alebo deliteľný štyrmi). 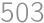 .
.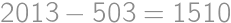 .
.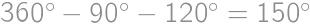 .
.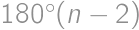 ,
,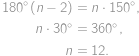
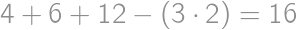 .
.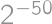
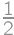 (bez ohľadu na to, ktoré dve čísla si vybral). Pre všetkých päťdesiat dvojíc teda máme pravdepodobnosť
(bez ohľadu na to, ktoré dve čísla si vybral). Pre všetkých päťdesiat dvojíc teda máme pravdepodobnosť 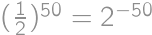 .
.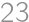
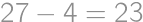 plechoviek.
plechoviek.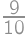
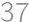
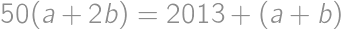 .
.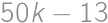 ,
,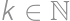 . Keby však bolo
. Keby však bolo 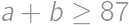 ,
,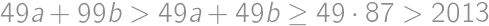 ,
,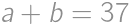 .
. ,
,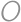 .
.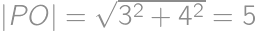 ,
,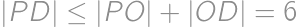 .
.
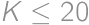 ). Ostatných
). Ostatných 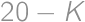 krabíc potom obsahuje po štyroch jablkách a my môžeme písať
krabíc potom obsahuje po štyroch jablkách a my môžeme písať 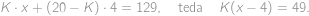
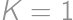 ,
,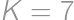 odpovedajúce po rade výsledkom
odpovedajúce po rade výsledkom 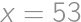 ,
,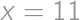 .
.
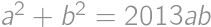 .
.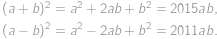
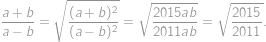
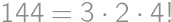
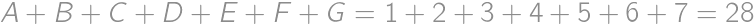 a
a 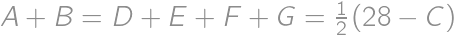 .
.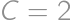 ,
,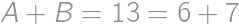 ,
,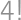 usporiadaní zvyšných čísel v spodnom riadku. Pre
usporiadaní zvyšných čísel v spodnom riadku. Pre 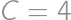 je
je 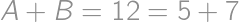 (
(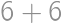 nevyhovuje, lebo všetky čísla majú byť navzájom rôzne) a pre
nevyhovuje, lebo všetky čísla majú byť navzájom rôzne) a pre 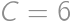 máme
máme 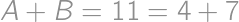 (
(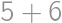 nevyhovuje, lebo už
nevyhovuje, lebo už 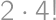 možností doplnenia tabuľky. Celkom dostávame
možností doplnenia tabuľky. Celkom dostávame 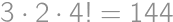 možnost??.
možnost??.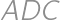 a
a 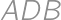 dáva
dáva 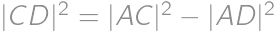 a
a 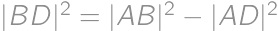 .
.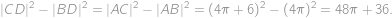
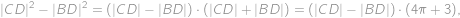
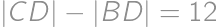 .
.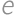 ,
,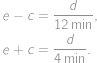
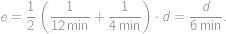
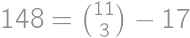
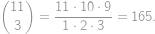
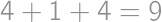 ,
,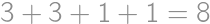 ,
,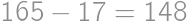 .
.
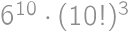
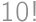 spôsobmi, vo všetkých troch riadkoch dohromady teda
spôsobmi, vo všetkých troch riadkoch dohromady teda 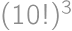 spôsobmi.
spôsobmi. 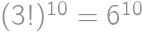 spôsobmi.
spôsobmi. 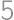
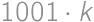 ,
,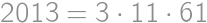 a z týchto troch prvočísel je
a z týchto troch prvočísel je 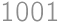 deliteľné iba jedenástimi, dostávame, že dvojité šesťciferné číslo je násobkom
deliteľné iba jedenástimi, dostávame, že dvojité šesťciferné číslo je násobkom 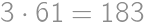 .
. je práve päť, a toľko je teda i šesťciferných dvojitých násobkov
je práve päť, a toľko je teda i šesťciferných dvojitých násobkov 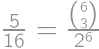
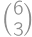 možných ciest. Pravdepodobnosť, že sa robot bude cesty držať, je v oboch prípadoch
možných ciest. Pravdepodobnosť, že sa robot bude cesty držať, je v oboch prípadoch 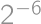 — každý zo šiestich krokov musí byť ten správny. Celková pravdepodobnosť je teda
— každý zo šiestich krokov musí byť ten správny. Celková pravdepodobnosť je teda 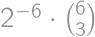 .
.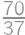
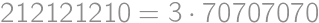 a
a 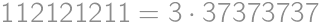 .
.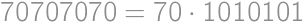 a
a 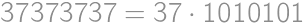 ,
,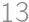
 .
. .
. .
.
 a
a  ,
,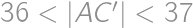 .
.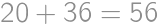 (
(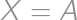 ) až k
) až k 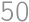 (
(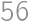 (
(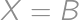 ). Celočíselnú hodnotu má teda pre
). Celočíselnú hodnotu má teda pre 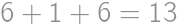 polôh bodu
polôh bodu 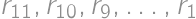 alebo
alebo 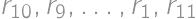 atď. až
atď. až 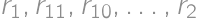
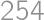
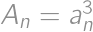 a ekvivalentne skúmajme, pre ktoré najmenšie prirodzené číslo
a ekvivalentne skúmajme, pre ktoré najmenšie prirodzené číslo 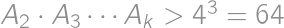 .
.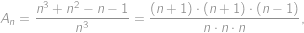
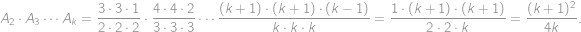
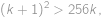
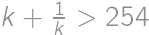 . Riešením je číslo 254.
. Riešením je číslo 254.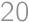
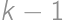 iných dielikov, teda „skokom“ o
iných dielikov, teda „skokom“ o 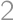 ,
, atď. Tieto skoky musia byť všetky v rovnakom smere, pretože prvým skokom v opačnom smere by sme sa dostali na predchádzajúci dielik s nižším číslom. Z dieliku
atď. Tieto skoky musia byť všetky v rovnakom smere, pretože prvým skokom v opačnom smere by sme sa dostali na predchádzajúci dielik s nižším číslom. Z dieliku  ,
,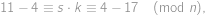
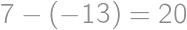 musí byť deliteľné
musí byť deliteľné 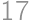 ,
, ,
,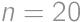 .
.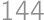
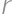 a
a 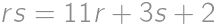 ,
,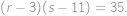
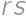 odpovedá prípadu
odpovedá prípadu 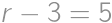 ,
,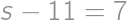 a je rovná
a je rovná 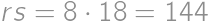 .
.
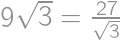
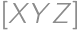 budeme označovať obsah trojuholníka
budeme označovať obsah trojuholníka 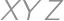 .
.
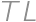 s kružnicou
s kružnicou 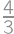 zobrazujúcim kružnicu
zobrazujúcim kružnicu 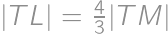 a
a 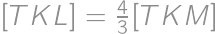 (trojuholníky zdieľajú výšku z vrcholu
(trojuholníky zdieľajú výšku z vrcholu 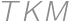 vpísaného do kružnice
vpísaného do kružnice 
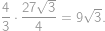
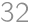
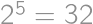 eur. Naopak Lukáš môže každým svojim ťahom znížiť rozdiel najväčšieho a najmenšieho čísla o polovicu tým, že odoberie spodnú alebo hornú časť množiny, a teda vie zaistiť, že Viktor vyhrá najviac
eur. Naopak Lukáš môže každým svojim ťahom znížiť rozdiel najväčšieho a najmenšieho čísla o polovicu tým, že odoberie spodnú alebo hornú časť množiny, a teda vie zaistiť, že Viktor vyhrá najviac 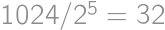 eur. Pri optimálnej hre obidvoch hráčov tak Viktor vyhrá 32 eur.
eur. Pri optimálnej hre obidvoch hráčov tak Viktor vyhrá 32 eur.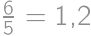 -krát
-krát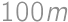 pôvodné priemerné IQ študentov Matfyzu a
pôvodné priemerné IQ študentov Matfyzu a 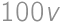 pôvodné priemerné IQ študentov VŠN. Nakoniec označme
pôvodné priemerné IQ študentov VŠN. Nakoniec označme 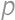 priemerné IQ študentov, ktorí prestúpili.
priemerné IQ študentov, ktorí prestúpili.  , je priemerné IQ zvyšných matfyzákov
, je priemerné IQ zvyšných matfyzákov 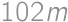 .
.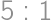 zvyšných matfyzákov k vyhodeným a z nového priemeru
zvyšných matfyzákov k vyhodeným a z nového priemeru 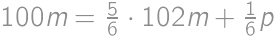 ,
,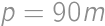 .
.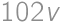 ,
,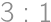 pôvodných študentov k novým máme
pôvodných študentov k novým máme 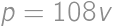 .
.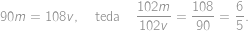
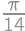
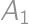 ,
,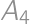 a
a 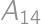 ešte na bod
ešte na bod 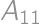 .
.
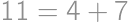 ,
,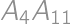 priemerom kružnice
priemerom kružnice 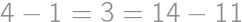 ,
,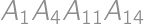 je rovnoramenný lichobežník a jeho základne
je rovnoramenný lichobežník a jeho základne 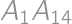 sú rovnobežné. Obsah trojuholníka
sú rovnobežné. Obsah trojuholníka 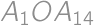 ,
,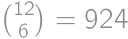
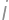 také, že
také, že 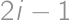 ,
,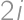 . Vezmeme najmenšie také
. Vezmeme najmenšie také 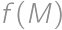 ,
,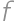 prevedieme na jednu množinu dvakrát po sebe, získame opäť pôvodnú množinu, a ďalej, že ak prevedieme
prevedieme na jednu množinu dvakrát po sebe, získame opäť pôvodnú množinu, a ďalej, že ak prevedieme 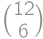 .
.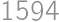
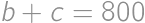 .
.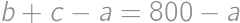 ,
, 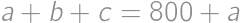 je deliteľné tromi, takže aby bolo súčasne prvočíslom, musí sa trom priamo rovnať. Keďže
je deliteľné tromi, takže aby bolo súčasne prvočíslom, musí sa trom priamo rovnať. Keďže 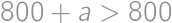 ,
, alebo
alebo 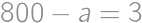 .
.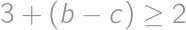 a súčasne
a súčasne 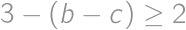 ,
,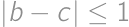 ,
,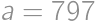 .
.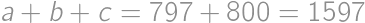 .
.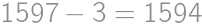 .
.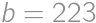 ,
, 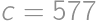 .
.
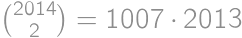 .
.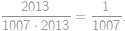
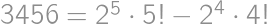
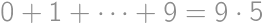 ,
,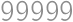 .
.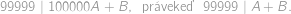
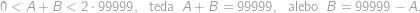
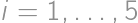 je
je 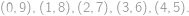
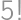 možností), a súčasne si pri každej dvojici môžeme vybrať, ktoré číslo z dvojice dáme do
možností), a súčasne si pri každej dvojici môžeme vybrať, ktoré číslo z dvojice dáme do 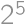 možností). Musíme však odčítať možnosti obsahujúce nulu na začiatku
možností). Musíme však odčítať možnosti obsahujúce nulu na začiatku 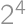 možností ako rozdeliť ich čísla medzi
možností ako rozdeliť ich čísla medzi 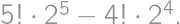
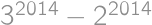
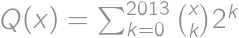 .
.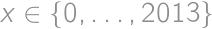 spĺňa podľa binomickej vety
spĺňa podľa binomickej vety 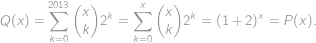
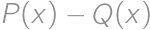 je stupňa 2013 a má 2014 koreňov, teda je nulový. Teda
je stupňa 2013 a má 2014 koreňov, teda je nulový. Teda 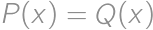 .
.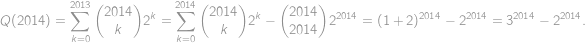
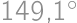
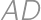 .
.
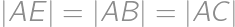 a
a 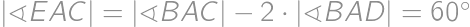 ,
,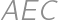 je rovnostranný a
je rovnostranný a 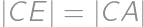 .
.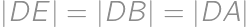 ,
,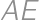 a
a 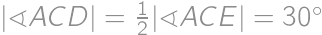 .
.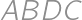 ľahko dopočítame
ľahko dopočítame 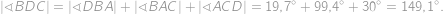
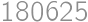
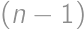 -ciferné
-ciferné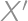 ).
).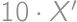 je opäť
je opäť 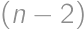 -ciferné číslo.
-ciferné číslo. 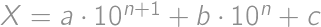 ,
,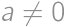 ) a
) a 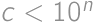 číslo nekončiace na nulu. Škrtnutím druhej cifry vznikne číslo
číslo nekončiace na nulu. Škrtnutím druhej cifry vznikne číslo 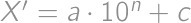 .
.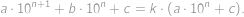
 .
. ,
,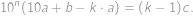
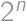 i
i 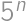 ,
,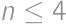 (lebo
(lebo 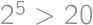 ,
, ),
), musí byť už nutne
musí byť už nutne 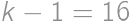 ,
,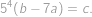
 (
(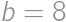 ,
,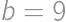 , z ktorých druhú zavrhujeme, lebo
, z ktorých druhú zavrhujeme, lebo 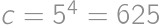 ,
,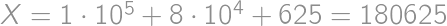 úlohu skutočne rieši.
úlohu skutočne rieši. 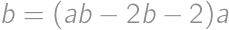 upravme na
upravme na 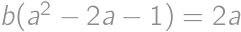 .
.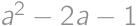 a tým získať vyjadrenie
a tým získať vyjadrenie 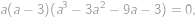
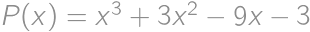 .
.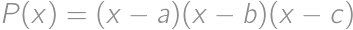 .
.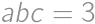 .
.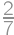
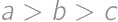 .
.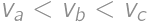 a
a 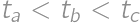 .
. ,
, a
a  ,
,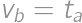 a
a 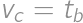 .
.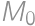 pätu kolmice z bodu
pätu kolmice z bodu 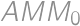 platí
platí 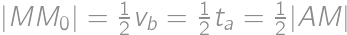 ,
, .
. stred strany
stred strany  .
.
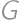 ťažisko trojuholníka
ťažisko trojuholníka 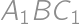 ,
,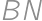 za ťažnicu. Bod
za ťažnicu. Bod 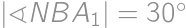 i
i 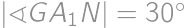 ,
,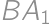 a kružnicového oblúka
a kružnicového oblúka 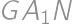 ,
,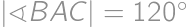 a
a 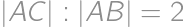 .
.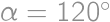 a dĺžkami strán
a dĺžkami strán 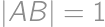 ,
,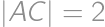 už ľahko z kosínusovej vety dopočítame dĺžku strany
už ľahko z kosínusovej vety dopočítame dĺžku strany  a dĺžku ťažnice
a dĺžku ťažnice 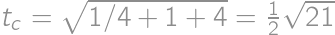 ,
, a nakoniec dĺžku výšky
a nakoniec dĺžku výšky 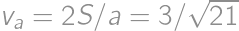 .
.