Zadanie 1
The numerator and denominator of Juan's fraction are positive integers whose sum is 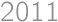 .
.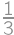 .
.
Pokaż / ukryj rozwiązanie
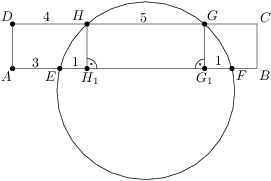
Zadanie 2
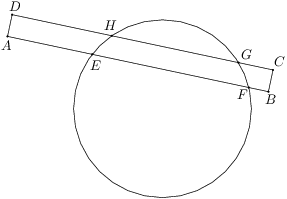
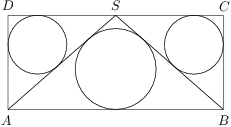
Rectangle 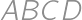 intersects a circle at points
intersects a circle at points 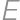 ,
,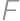 ,
, 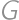 ,
, as shown in the diagram. If
as shown in the diagram. If 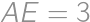 ,
,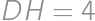 , and
, and 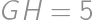 ,
, .
.
Pokaż / ukryj rozwiązanie
Zadanie 3
Find the sum of digits of the number 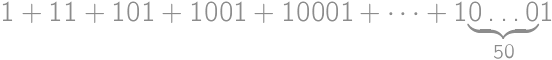 .
.
Pokaż / ukryj rozwiązanie
Zadanie 4
T-shirts were made in three colors, red, gray and blue. The number of red T-shirts is six smaller than the total number blue and gray T-shirts. Also, the number of gray T-shirts is ten smaller than the total number red and blue T-shirts. How many blue T-shirts were made?
Pokaż / ukryj odpowiedźPokaż / ukryj rozwiązanie
Zadanie 5
There are 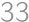 walnuts on the table in at least two piles. Each pile consists of at least
walnuts on the table in at least two piles. Each pile consists of at least 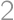 walnuts. After moving one walnut from each pile to the first one, all piles will have the same number of walnuts. What was the original number of piles? Find all possibilities.
walnuts. After moving one walnut from each pile to the first one, all piles will have the same number of walnuts. What was the original number of piles? Find all possibilities.
Pokaż / ukryj rozwiązanie
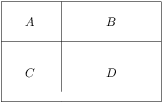
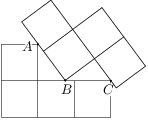
Zadanie 6
A rectangle is divided by two segments parallel to its sides into four smaller rectangles. Let's label them  ,
,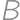 ,
, 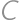 ,
,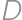 as in the diagram. Given that the perimeters of rectangles
as in the diagram. Given that the perimeters of rectangles 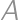 ,
,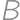 ,
, 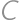 are
are 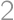 ,
,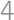 , and
, and 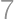 ,
,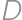 .
.
Pokaż / ukryj rozwiązanie
Zadanie 7
Find pairwise distinct digits 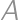 ,
,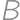 ,
, 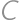 such that
such that
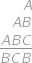
Pokaż / ukryj rozwiązanie
Zadanie 8
Find the area of a rectangle with perimeter 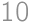 cm and diagonal
cm and diagonal 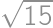 cm.
cm.
Pokaż / ukryj rozwiązanie
Zadanie 9
Andrei took 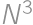 equally sized white cubes and used them to form one big cube
equally sized white cubes and used them to form one big cube 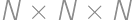 .
.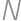 .
.
Pokaż / ukryj rozwiązanie
Zadanie 10
What is the least possible number of members of a math circle, where girls form more than 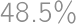 but less than
but less than 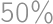 of the members?
of the members?
Pokaż / ukryj rozwiązanie
Zadanie 11
If you increase the number of this problem by  ,
, ,
,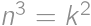 .
.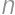 and
and 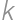 ,
,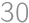 problems left (including this one).
problems left (including this one).
Pokaż / ukryj rozwiązanie
Zadanie 12
Find positive integer 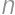 such that
such that 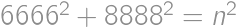 .
.
Pokaż / ukryj rozwiązanie
Zadanie 13
Find the smallest positive integer, which ends with number 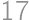 ,
,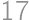 ,
,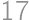 .
.
Pokaż / ukryj rozwiązanie
Zadanie 14
Each pair of consecutive digits of a 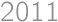 -digit
-digit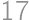 or
or 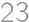 .
.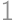 .
.
Pokaż / ukryj rozwiązanie
Zadanie 15
A positive integer is called awesome if any other positive integer with the same sum of digits is greater. How many three-digit awesome numbers exist?
Pokaż / ukryj odpowiedźPokaż / ukryj rozwiązanie
Zadanie 16
Tim has found real numbers 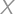 ,
,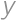 ,
, 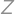 satisfying
satisfying 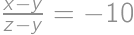 .
.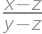 ?
?
Pokaż / ukryj rozwiązanie
Zadanie 17
The numbers  are arranged in some order to form a nine-digit integer. Consider all triplets of consecutive digits and add the corresponding seven three-digit numbers. What is the largest result that can be obtained?
are arranged in some order to form a nine-digit integer. Consider all triplets of consecutive digits and add the corresponding seven three-digit numbers. What is the largest result that can be obtained?
Pokaż / ukryj rozwiązanie
Zadanie 18
A real number is written in each cell of a 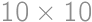 square. Emily wrote down all products of two numbers from two distinct cells of the table and noticed that exactly
square. Emily wrote down all products of two numbers from two distinct cells of the table and noticed that exactly 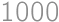 of these products were negative. How many times did number
of these products were negative. How many times did number 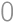 appear in the original square? Find all possibilities.
appear in the original square? Find all possibilities.
Pokaż / ukryj rozwiązanie
Zadanie 19
Math kingdom started to produce a new set of coins. On the first day they created coins with value 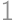 MD (Math Dollar). Every other day they created coins with the smallest value which cannot be paid by at most ten existing coins. Which coins did they create on the
MD (Math Dollar). Every other day they created coins with the smallest value which cannot be paid by at most ten existing coins. Which coins did they create on the 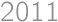 th
th
Pokaż / ukryj rozwiązanie
Zadanie 20
Let the number 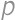 be the solution to this problem. Find the probability that a randomly chosen point inside a unit square is at least
be the solution to this problem. Find the probability that a randomly chosen point inside a unit square is at least 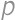 units away from all sides.
units away from all sides.
Pokaż / ukryj rozwiązanie
Zadanie 21
A 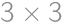 square is filled with integers such that the sums of the horizontal rows increase by two going downwards and the sums of the vertical columns double from left to right. Given that the sum of the numbers in one of the rows is
square is filled with integers such that the sums of the horizontal rows increase by two going downwards and the sums of the vertical columns double from left to right. Given that the sum of the numbers in one of the rows is 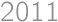 ,
,
Pokaż / ukryj rozwiązanie
Zadanie 22
There are 2 boats, one on each side of a river bank. They both sail towards each other at a constant speed (not necessarily the same). The first time they meet, they are 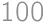 meters from one side of the bank. Once they reach the side of the bank, they turn around and move towards each other again. This time they meet
meters from one side of the bank. Once they reach the side of the bank, they turn around and move towards each other again. This time they meet  meters from the other side of the bank. How wide is the river?
meters from the other side of the bank. How wide is the river?
Pokaż / ukryj rozwiązanie
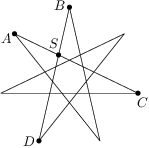
Zadanie 23
Vertices of a star form a regular heptagon. What is the magnitude of the marked angle?
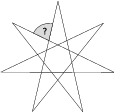
Pokaż / ukryj rozwiązanie
Zadanie 24
Find  such that
such that 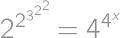 .
.
Note: the order of operations is: 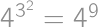 .
.
Pokaż / ukryj rozwiązanie
Zadanie 25
How many triplets of positive integers 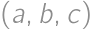 exist, such that
exist, such that
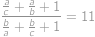
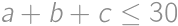 ?
?Pokaż / ukryj rozwiązanie
Zadanie 26
A circle 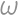 with radius
with radius 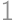 ,
,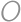 and diameter
and diameter 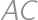 is given in the plane. Draw a line
is given in the plane. Draw a line 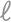 through point
through point  such that it is perpendicular to
such that it is perpendicular to 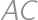 .
. on
on 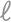 such that
such that 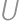 is outside
is outside 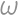 .
.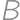 the second intersection of
the second intersection of 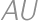 and
and 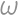 and assume
and assume 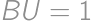 .
.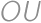 .
.
Pokaż / ukryj rozwiązanie
Zadanie 27
Two nations 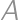 and
and 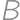 are in a battle with
are in a battle with 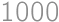 soldiers involved altogether. The armies take turns to attack. In each turn every living soldier from the attacking army shoots a soldier from the enemy's army. The battle ended (not necessarily by elimination of one of the sides) after three turns (
soldiers involved altogether. The armies take turns to attack. In each turn every living soldier from the attacking army shoots a soldier from the enemy's army. The battle ended (not necessarily by elimination of one of the sides) after three turns (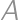 was shooting first, then
was shooting first, then 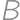 and finally
and finally 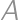 again). What is the least guaranteed number of survivors?
again). What is the least guaranteed number of survivors?
Pokaż / ukryj rozwiązanie
Zadanie 28
All six sides of a convex hexagon 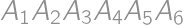 are colored in red. Each of the diagonals is either blue or red. Find the number of such colorings that each triangle
are colored in red. Each of the diagonals is either blue or red. Find the number of such colorings that each triangle 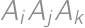 (
(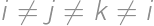 ) has at least one red side.
) has at least one red side.
Pokaż / ukryj rozwiązanie
Zadanie 29
Malcom told each Michal and Shri a positive integer. Further, he told them, that the numbers they heard were distinct and that their sum is a two-digit number. Then the following conversation took place:
Michal: ”I cannot determine which one of us has the greater number.”
Shri: ”I can't determine it either, but I will tell you that my number is divisible by 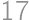 .”
.”
Michal: ”Wow! Now, I can determine the sum of our numbers.”
Find the value of this sum, given that the logic Michal and Shri used was flawless.
Pokaż / ukryj odpowiedźPokaż / ukryj rozwiązanie
Zadanie 30
There are 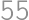 guests in a café, Turks and Indians. Each of them drinks either tea or coffee. An Indian speaks truth if he drinks tea and lies if he drinks coffee, whereas with the Turks it is the other way round. For questions ”Do you drink coffee?”, ”Are you Turkish?” and ”Is it raining outside?” the numbers of positive answers were
guests in a café, Turks and Indians. Each of them drinks either tea or coffee. An Indian speaks truth if he drinks tea and lies if he drinks coffee, whereas with the Turks it is the other way round. For questions ”Do you drink coffee?”, ”Are you Turkish?” and ”Is it raining outside?” the numbers of positive answers were 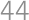 ,
,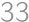 , and
, and 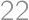 ,
,
Pokaż / ukryj rozwiązanie
Zadanie 31
Three digits were written to the end of a positive integer  .
. to
to 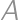 .
.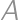 .
.
Pokaż / ukryj rozwiązanie
Zadanie 32
Alice, Betty, Claudia, Daniel, and Eli were playing doubles tournament in table-tennis. Each pair played against each other pair exactly once. Alice won 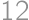 games and Betty won
games and Betty won 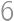 games. How many games could Claudia win? Find all possibilities.
games. How many games could Claudia win? Find all possibilities.
Pokaż / ukryj rozwiązanie
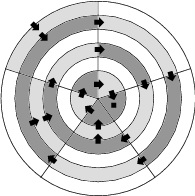
Zadanie 33
Two players are playing a game on the given plan consisting of 30 cells. The rules are the following.
- players take turns,
- in one move a player colors one cell,
- in the first move, only a cell neighbouring with the edge can be colored. In any other moves, only a cell which is next to the last colored cell and is not further away from the center, can be colored,
- once a cell is colored, it cannot be colored again.
- the player who can no longer make a move, loses.
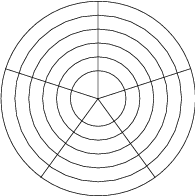
Pokaż / ukryj rozwiązanie
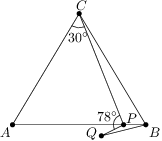
Zadanie 34
In triangle 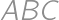 with
with 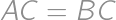 ,
,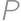
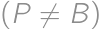 on the side
on the side 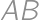 ,
,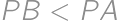 and
and 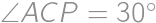 .
. such that
such that 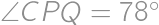 and points
and points 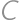 and
and  lie each on opposite side of
lie each on opposite side of 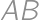 .
.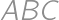 and
and 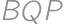 have integral values (in degrees), find all possible values of angle
have integral values (in degrees), find all possible values of angle 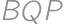 .
.
Pokaż / ukryj rozwiązanie
Zadanie 35
Ten people in the theater are sitting next to each other in one row. After a break they sit in a new arrangement, so that only two people remained in their original positions and the remaining eight sat next to their former position. In how many ways could they have done that?
Pokaż / ukryj odpowiedźPokaż / ukryj rozwiązanie
Zadanie 36
A positive integer is written on each face of a cube. To each vertex we assign the product of the numbers written on the three faces intersecting at that vertex. The sum of the numbers assigned to the vertices is 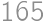 .
.
Pokaż / ukryj rozwiązanie
Zadanie 37
Two bicyclists are racing on a straight path at constant speeds. They both start at one end and everytime they hit the end of the path, they turn around and go the opposite direction. Eventually, they meet again at one of the endpoints. Before that, the slower bicyclist had traveled the path 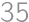 times (in one of the directions) and the faster one
times (in one of the directions) and the faster one 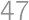 times. How many times did they meet head on?
times. How many times did they meet head on?
Pokaż / ukryj rozwiązanie
Zadanie 38
Find the largest positive integer such that all its digits (other than the first one and the last one) are smaller than the arithmetic mean of the two surrounding digits.
Pokaż / ukryj odpowiedźPokaż / ukryj rozwiązanie
Zadanie 39
Two tetrominoes made of 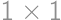 squares touch at points
squares touch at points 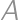 ,
,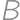 ,
, 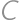 as in the diagram. Find the distance
as in the diagram. Find the distance 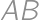 .
.
Pokaż / ukryj rozwiązanie
Zadanie 40
There are 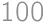 points with integral coordinates given in the plane. We connect each pair with a segment. How many of these segments are guaranteed to have a midpoint with integral coordinates?
points with integral coordinates given in the plane. We connect each pair with a segment. How many of these segments are guaranteed to have a midpoint with integral coordinates?
Pokaż / ukryj rozwiązanie
Zadanie 41
A five-digit integer is called irreducible if it cannot be written as a product of two three-digit integers. What is the maximum possible number of consecutive irreducible integers?
Pokaż / ukryj odpowiedźPokaż / ukryj rozwiązanie
Zadanie 42
Real numbers 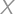 and
and 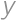 satisfy
satisfy 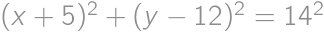 .
.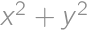 .
.
Pokaż / ukryj rozwiązanie
Zadanie 43
A sequence is definned as follows: 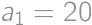 ,
,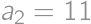 , and
, and
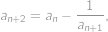
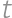 such that
such that 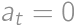 .
.Pokaż / ukryj rozwiązanie
Zadanie 44
Let 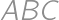 be an acute-angled triangle with altitudes
be an acute-angled triangle with altitudes 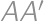 ,
,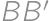 ,
, 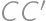 ,
, .
.
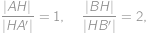
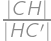 .
.Pokaż / ukryj rozwiązanie
Zadanie 45
Every guest at a party (including Tim) knows exactly seven boys and ten girls there. What is the least possible number of people at the party?
Pokaż / ukryj odpowiedźPokaż / ukryj rozwiązanie
Zadanie 46
Let 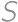 be the midpoint of side
be the midpoint of side 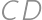 of rectangle
of rectangle 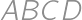 .
.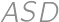 and
and 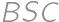 have radii both equal to
have radii both equal to 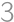 and the inradius of
and the inradius of 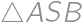 is
is 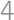 .
.
Pokaż / ukryj rozwiązanie
Zadanie 47
We write out all divisors of a positive integer  which are less than
which are less than  from the greatest to the lowest. If
from the greatest to the lowest. If 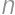 is the sum of the second and third divisor, we say that
is the sum of the second and third divisor, we say that 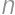 is additive. How many additive numbers are there which are less than
is additive. How many additive numbers are there which are less than 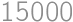 ?
?
Pokaż / ukryj rozwiązanie
Zadanie 48
Find all real numbers 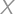 such that
such that
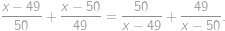
Pokaż / ukryj rozwiązanie
Zadanie 49
A position of a minute hand and an hour hand on the clock is called valid, if it might occur during one  hour cycle. Find the number of valid positions which remain valid after switching the two hands.
hour cycle. Find the number of valid positions which remain valid after switching the two hands.
Pokaż / ukryj rozwiązanie
Zadanie 50
Let 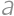 ,
,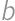 ,
, 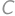 be nonzero real numbers, such that the quadratic equations
be nonzero real numbers, such that the quadratic equations 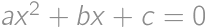 and
and 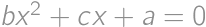 have a common root. Find all possible real values of this root.
have a common root. Find all possible real values of this root.
Pokaż / ukryj rozwiązanie
Zadanie 51
Find all integers 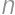 such that both
such that both 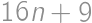 and
and 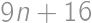 are perfect squares.
are perfect squares.
Pokaż / ukryj rozwiązanie
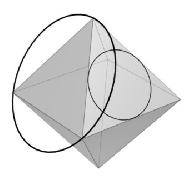
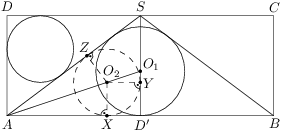
Zadanie 52
A regular octahedron with side length 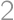 is given in space. One circle is inscribed in one of the faces and another circle is circumscribed about an adjacent face. What is the minimal distance between the two circles?
is given in space. One circle is inscribed in one of the faces and another circle is circumscribed about an adjacent face. What is the minimal distance between the two circles?
Pokaż / ukryj rozwiązanie
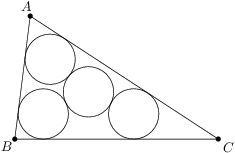
Zadanie 53
Let  be a triangle with circumradius
be a triangle with circumradius  and inradius
and inradius  .
. are inscribed in angles
are inscribed in angles 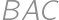 ,
,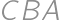 ,
, 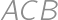 ,
,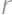 which is tangent to all three circles. Find
which is tangent to all three circles. Find  .
.
Pokaż / ukryj rozwiązanie
Zadanie 54
Real numbers 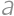 ,
,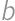 ,
, 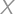 ,
,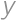 satisfy
satisfy
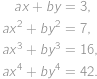
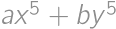 .
.Pokaż / ukryj rozwiązanie
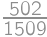 .
.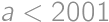 ,
,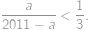
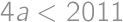 , from which we get that the biggest value of a is
, from which we get that the biggest value of a is 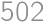 ,
,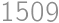 ,
,
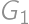 ,
,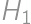 be the projections of
be the projections of 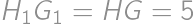 .
.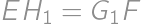 and
and 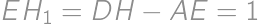 ,
,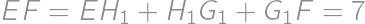 .
.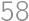 .
.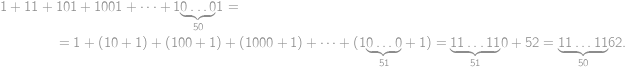
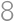 .
.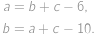
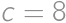 .
.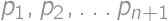 be all the piles. Then
be all the piles. Then 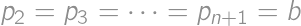 ,
,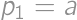 .
.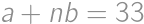 and
and 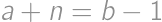 ,
,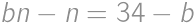 ,
,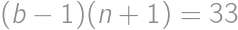 .
.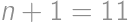 ,
, ,
,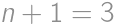 ,
, cm.
cm.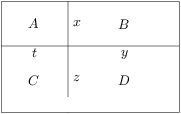
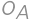 ,
,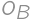 ,
, 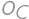 ,
,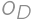 be the perimeters of the rectangles
be the perimeters of the rectangles 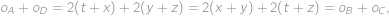
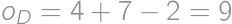 cm.
cm.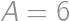 ,
,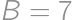 ,
, 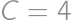 .
.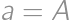 ,
,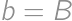 ,
, 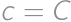 .
.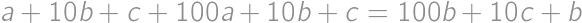 ,
,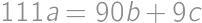 .
.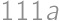 ,
, ,
,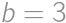 and
and 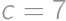 ,
,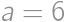 ,
, and
and 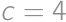 .
.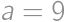 ,
,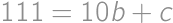 ,
,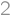 .
.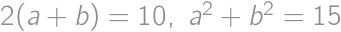 ,
,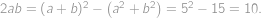
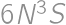 ,
,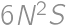 .
.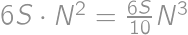 ,
,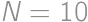 .
.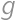 be the number of girls in the math circle, and let
be the number of girls in the math circle, and let 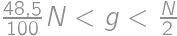 ,
,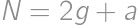 ,
,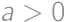 ,
,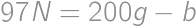 ,
,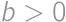 .
.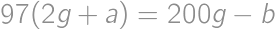 ,
,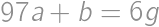 .
. ,
, ,
,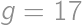 and
and 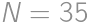 .
.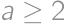 ,
, ,
,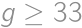 ,
, .
.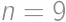 ,
,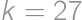 .
.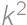 to be a cube,
to be a cube, 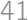 is
is 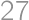 ,
,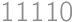 .
.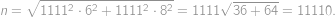
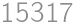 .
.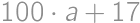 for some
for some 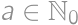 .
.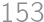 ,
,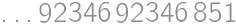 .
. of the sum of the digits there is exactly one smallest positive integer with this sum of its digits, i.e. one awesome number. Let's denote it
of the sum of the digits there is exactly one smallest positive integer with this sum of its digits, i.e. one awesome number. Let's denote it  .
.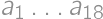 will be two digit integers, whereas
will be two digit integers, whereas 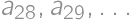 will have more than three digits. Also the sums of digits of three-digit integers attain all numbers between
will have more than three digits. Also the sums of digits of three-digit integers attain all numbers between 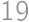 and
and  will indeed have three digits and thus we have
will indeed have three digits and thus we have 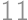 .
.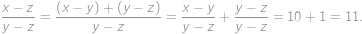
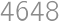 .
.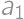 ,
,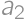 , … ,
, … , 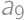 .
.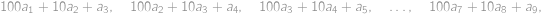
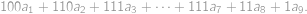
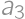 to
to 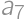 the highest digits and
the highest digits and 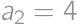 ,
,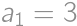 ,
, 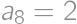 ,
,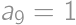 . The result is
. The result is 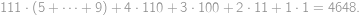
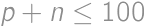 and
and 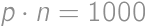 ,
,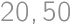 and
and 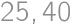 ,
,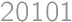 .
.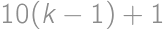 .
.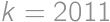 .
.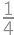 .
.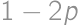 .
.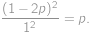
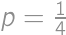 works,
works, 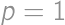 does not.
does not.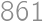 .
.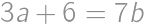 .
.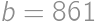 .
.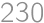 m.
m.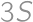 meters. For the boat which had travelled
meters. For the boat which had travelled 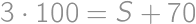 ,
, .
. .
.
 ,
,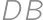 .
.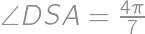 and
and 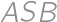 is supplementary.
is supplementary.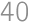 .
.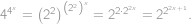
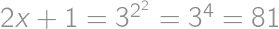 ,
,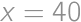 .
.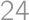 .
.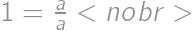 and
and 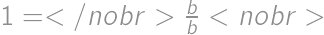 to get
to get 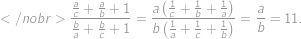
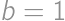 ,
,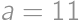 we get
we get 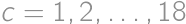 and for
and for  ,
,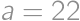 we get
we get 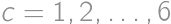 ,
,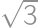 .
.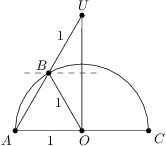
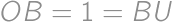 ,
,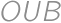 is isosceles. Thus
is isosceles. Thus  and also on its hypotenuse, so it is the midpoint of the hypotenuse. Thus
and also on its hypotenuse, so it is the midpoint of the hypotenuse. Thus 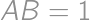 and Pythagorean theorem gives
and Pythagorean theorem gives 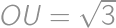 .
. .
. soldiers at the beginning of the battle. Also note that
soldiers at the beginning of the battle. Also note that 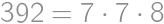 .
.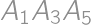 and
and 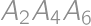 (dashed in the diagram) all other triangles have a red edge. Every dashed triangle can be colored in
(dashed in the diagram) all other triangles have a red edge. Every dashed triangle can be colored in 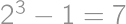 ways. Finally, we have
ways. Finally, we have 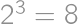 ways to color the dotted diagonals
ways to color the dotted diagonals 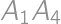 ,
,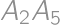 ,
, 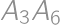 .
.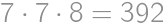 suitable colorings.
suitable colorings. 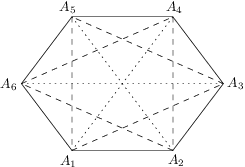
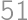 .
.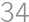 .
.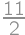 Indians drinking tea, which is against humanity. The other solution works and yields
Indians drinking tea, which is against humanity. The other solution works and yields 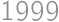 .
.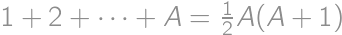 ,
,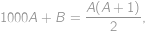
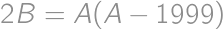 .
.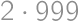 ,
,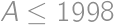 and greater than
and greater than 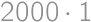 for
for 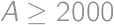 .
.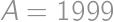 which satisfies the problem for
which satisfies the problem for 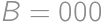 .
.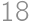 .
.
 .
.
 and
and 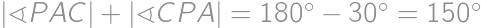 ,
,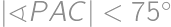 .
.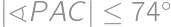 a
a 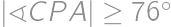 .
.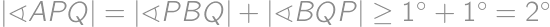 ,
,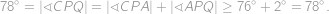
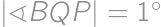 .
.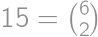 .
.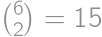 such sequences.
such sequences.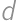 ,
, 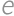 ,
,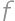 so that the pairs
so that the pairs 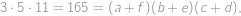
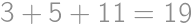 .
.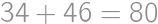 changes of direction, which means
changes of direction, which means 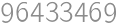 .
.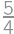

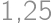 .
.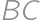 are congruent by
are congruent by 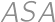 .
.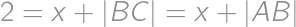 a by Pythagorean theorem also
a by Pythagorean theorem also 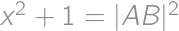 .
.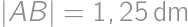 .
.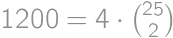 .
.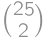 midpoints with integers coordinates so the answer is
midpoints with integers coordinates so the answer is 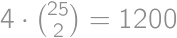
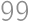 .
.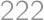 .
.
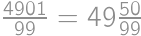 .
.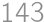 .
.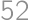 .
.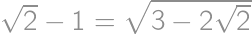 .
.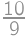 .
.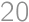 .
.