Úloha 1
Kvádr s délkami hran 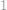 ,
,  ,
, 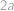 má povrch
má povrch 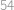 . Najděte hodnotu čísla
. Najděte hodnotu čísla  .
.
Zobraziť / skryť výsledok
 .
.
Úloha 2
Pomocí právě tří osmiček a libovolných ze symbolů 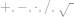 vytvořte číslo
vytvořte číslo  . Jeden symbol můžete použít i víckrát.
. Jeden symbol můžete použít i víckrát.
Zobraziť / skryť výsledok
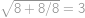 .
.
Prostě se to musí uvidět.
Úloha 3
Vejtek měl knihu z teorie množin, jejíž listy byly číslované postupně  ,
, 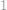 ,
,  ,
,  ,
,  Afro mu z ní jeden list vytrhnul. Teď je součet čísel na zbylých listech
Afro mu z ní jeden list vytrhnul. Teď je součet čísel na zbylých listech 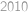 . List se kterým číslem Afro vytrhnul?
. List se kterým číslem Afro vytrhnul?
Zobraziť / skryť výsledok
List s číslem  .
.
Úloha 4
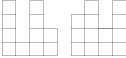
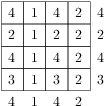
Alča postavila stavbu z několika jednotkových kostek, která se vejde do větší kostky rozměrů 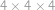 . Pepovi však nakreslila jen pohledy postupně z jihu a z východu. Najděte největší a nejmenší počet kostek, ze kterých může být stavba postavená, pokud máte stejně jako Pepa k dispozici pouze tento obrázek.
. Pepovi však nakreslila jen pohledy postupně z jihu a z východu. Najděte největší a nejmenší počet kostek, ze kterých může být stavba postavená, pokud máte stejně jako Pepa k dispozici pouze tento obrázek.
Zobraziť / skryť výsledok
Nejméně 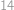 kostek, nejvíce
kostek, nejvíce 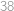 .
.
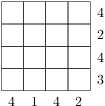
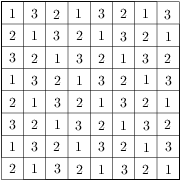
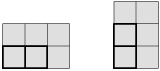
Když se podíváme na stavbu shora, vidíme následující tabulku:
Čísla vedle řádků, resp. sloupců znamenají největší počet kostek na jednom políčku v daném řádku, resp. sloupci. Chceme-li, aby stavba obsahovala co nejvíce kostek, postavíme na každé políčko největší přípustný počet kostek, tj. menší ze zadaných maxim v daném řádku a sloupci. Výsledná tabulka vypadá takto:
Hledaný největší počet kostek je součet všech čísel v tabulce, tedy
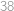 .
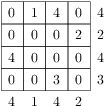
. Nyní najdeme nejmenší možný počet použitých kostek. Všimneme si, že podmínky pro maxima vynucují, aby bylo alespoň jedno políčko s právě jednou kostkou, alespoň jedno se dvěma kostkami, jedno se třemi a dvě se čtyřmi — vždy tedy musíme použít alespoň 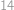 kostek. Snadno však kostky rozestavíme tak, aby jich nebylo více než tento dolní odhad, např. takto:
kostek. Snadno však kostky rozestavíme tak, aby jich nebylo více než tento dolní odhad, např. takto:
Nejméně tedy může být na stavbu použito
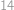
kostek.
Úloha 5
Blecha skáče po mřížových bodech čtverečkové sítě. Každým skokem se dostane o jeden mřížový bod výš, níž, doprava nebo doleva. Začne skákat z bodu 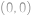 . Do kolika mřížových bodů se může dostat přesně po deseti skocích?
. Do kolika mřížových bodů se může dostat přesně po deseti skocích?
Zobraziť / skryť výsledok
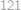 .
.
Úloha 6
Kolik existuje tříprvkových podmnožin množiny 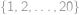 takových, že součin jejich prvků je dělitelný čtyřmi?
takových, že součin jejich prvků je dělitelný čtyřmi?
Zobraziť / skryť výsledok
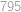 .
.
Úloha 7
V aritmetické posloupnosti 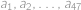 je součet členů s lichými indexy rovný
je součet členů s lichými indexy rovný 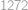 . Zjistěte součet všech členů této posloupnosti.
. Zjistěte součet všech členů této posloupnosti.
Zobraziť / skryť výsledok
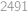 .
.
Úloha 8
V lichoběžníku 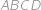 (se základnami
(se základnami 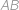 a
a  ) platí
) platí 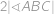 =
= 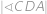 . Dále víme, že
. Dále víme, že 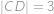 cm a
cm a 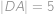 cm. Zjistěte velikost úsečky
cm. Zjistěte velikost úsečky 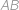 .
.
Zobraziť / skryť výsledok
 cm.
cm.
V lichoběžníku vyznačme osu úhlu 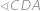 a označme
a označme 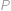 její průsečík se stranou
její průsečík se stranou 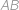 :
:
Protože
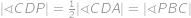 ,
, je
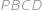
rovnoběžník a
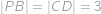 cm.
cm. Dále díky rovnosti
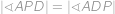
je trojúhelník
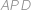
rovnoramenný (se základnou
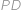 ),
), a tedy
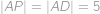 cm.
cm. Hledanou velikost zjistíme jako
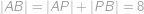
cm.
Úloha 9
Tři planety 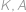 a
a 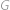 obíhají kolem hvězdy
obíhají kolem hvězdy 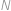 po soustředných kružnicových dráhách (společný střed kružnic je hvězda
po soustředných kružnicových dráhách (společný střed kružnic je hvězda 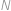 ). Pohybují se konstantní rychlostí a mají různé periody oběhu:
). Pohybují se konstantní rychlostí a mají různé periody oběhu: 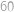 ,
, 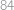 a
a 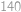 roků. Jednou se stalo, že tyto tři planety spolu s hvězdou
roků. Jednou se stalo, že tyto tři planety spolu s hvězdou 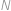 ležely na jedné přímce. Kolik nejméně roků musí uplynout, aby
ležely na jedné přímce. Kolik nejméně roků musí uplynout, aby 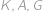 a
a 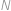 znovu ležely na jedné přímce?
znovu ležely na jedné přímce?
Zobraziť / skryť výsledok
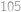 roků.
roků.
Podívejme se nejprve, kdy budou hvězdy 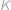 a
a  znova ležet s
znova ležet s 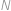 na jedné přímce. Bude to tehdy, když (rychlejší) hvězda
na jedné přímce. Bude to tehdy, když (rychlejší) hvězda 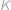 oběhne o polovinu dráhy více než hvězda
oběhne o polovinu dráhy více než hvězda  , neboli pro počet oběhů
, neboli pro počet oběhů  hvězdy
hvězdy  musí platit
musí platit 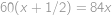 , z čehož jednoduše plyne
, z čehož jednoduše plyne 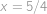 . Tutéž myšlenku provedeme pro hvězdy
. Tutéž myšlenku provedeme pro hvězdy  a
a 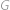 , kde
, kde 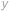 označíme počet oběhů hvězdy
označíme počet oběhů hvězdy  za dobu, než se
za dobu, než se 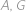 a
a 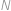 znova srovnají do přímky. Dostaneme rovnici
znova srovnají do přímky. Dostaneme rovnici 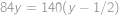 a řešení
a řešení 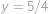 . Jelikož
. Jelikož 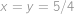 , tak za dobu, kdy hvězda
, tak za dobu, kdy hvězda  oběhne celkem
oběhne celkem 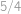 své dráhy, což je
své dráhy, což je 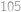 roků, budou všechny hvězdy opět na jedné přímce.
roků, budou všechny hvězdy opět na jedné přímce.
Úloha 10
Monča se v jednom svém snu ocitla v jedné zapadlé rovině. Nacházela se v bodě se souřadnicemi 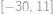 a vydala sa po přímce až do bodu
a vydala sa po přímce až do bodu 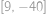 . Kolik mřížových bodů (mřížový bod je takový, který má obě souřadnice celočíselné) cestou navštívila? Započítejte i počáteční a koncový bod.
. Kolik mřížových bodů (mřížový bod je takový, který má obě souřadnice celočíselné) cestou navštívila? Započítejte i počáteční a koncový bod.
Zobraziť / skryť výsledok
 .
.
Úloha 11
Miloš má svoje oblíbené přirozené číslo. Víme, že je to nejmenší přirozené číslo  takové, že čísla
takové, že čísla  ,
,  mají obě ciferný součet dělitelný číslem
mají obě ciferný součet dělitelný číslem 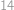 . Najděte Milošovo oblíbené číslo.
. Najděte Milošovo oblíbené číslo.
Zobraziť / skryť výsledok
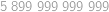 .
.
Úloha 12
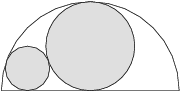
Mějme půlkruh s poloměrem 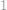 . Do něho vepíšeme největší kruh, jaký se vejde, a vybarvíme ho šedě. Potom do nešedého zbytku půlkruhu vepíšeme největší kruh, jaký se vejde, tak, aby průnik s šedým kruhem byl nanejvýš jednobodový. Jaký poloměr má menší kruh?
. Do něho vepíšeme největší kruh, jaký se vejde, a vybarvíme ho šedě. Potom do nešedého zbytku půlkruhu vepíšeme největší kruh, jaký se vejde, tak, aby průnik s šedým kruhem byl nanejvýš jednobodový. Jaký poloměr má menší kruh?
Zobraziť / skryť výsledok
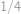 .
.
Body si označíme jako na obrázku.  je střed půlkruhu,
je střed půlkruhu,  střed šedého kruhu,
střed šedého kruhu,  střed malého kruhu,
střed malého kruhu, 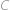 je jeho bod dotyku s poloměrem půlkruhu,
je jeho bod dotyku s poloměrem půlkruhu, 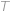 je bod dotyku půlkruhu a malého kruhu a
je bod dotyku půlkruhu a malého kruhu a 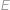 je pata kolmice z
je pata kolmice z  na
na 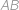 .
.
Poloměr šedého kruhu označíme
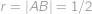 ,
, poloměr malého kruhu bude
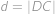 .
. Víme:
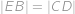 ,
, 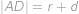
,
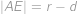 ,
, 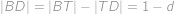
. Trojúhelník
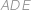
je pravoúhlý (s pravým úhlem u
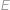 ),
), tedy z Pythagorovy věty platí:
 .
. Trojúhelník
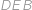
je rovněž pravoúhlý (s pravým úhlem u
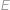 ),
), takže podle Pythagorovy věty:
 .
. Dosazením do druhé rovnice dostáváme:
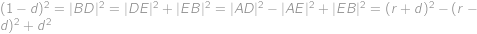 .
. Po roznásobení:
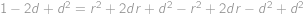
a po odečtení:
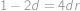 .
. Poloměr

známe (
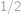
), tedy
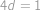 ,
, 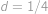
.
Úloha 13
Kolika způsoby můžeme z 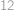 různých hráčů sestavit tři týmy po čtyřech hráčích?
různých hráčů sestavit tři týmy po čtyřech hráčích?
Zobraziť / skryť výsledok
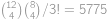 .
.
Úloha 14
Vyčíslete výraz 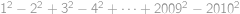 .
.
Zobraziť / skryť výsledok
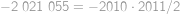 .
.
Označme 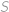 hledaný součet. Členy řady „chytře“ uzávorkujeme a použijeme vzorec pro rozdíl druhých mocnin:
hledaný součet. Členy řady „chytře“ uzávorkujeme a použijeme vzorec pro rozdíl druhých mocnin:
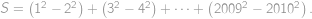
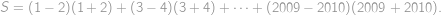
Je patrné, že všechny závorky obsahující rozdíl mají hodnotu
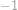 .
. Dostáváme tedy
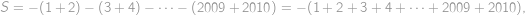
což už snadno vyčíslíme dosazením do známého vzorce
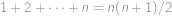 .
.
Úloha 15
Auto jede z kopce rychlostí  km/h, po rovině rychlostí
km/h, po rovině rychlostí  km/h a do kopce rychlostí
km/h a do kopce rychlostí 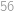 km/h. Cesta z města
km/h. Cesta z města  do města
do města  trvá
trvá  hodiny. Zpáteční cesta trvá
hodiny. Zpáteční cesta trvá  hodiny a
hodiny a  minut. Jaká je vzdálenost po cestě mezi městy
minut. Jaká je vzdálenost po cestě mezi městy  a
a  ?
?
Zobraziť / skryť výsledok
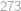 km.
km.
Označme 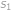 ,
, 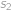 resp.
resp. 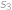 vzdálenosti, které je při cestě z
vzdálenosti, které je při cestě z  do
do  potřeba ujet z kopce, po rovině resp. do kopce. Při cestě zpět bude z kopce to, co bylo cestou tam do kopce a naopak, takže platí
potřeba ujet z kopce, po rovině resp. do kopce. Při cestě zpět bude z kopce to, co bylo cestou tam do kopce a naopak, takže platí
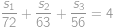
a
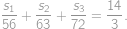
Sečtením obdržíme
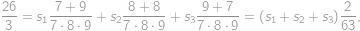
takže hledaná vzdálenost je
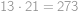
km.
Úloha 16
Na matfyzu máme podivný bankomat. Když k němu Honzík naposledy přišel, byla v něm hotovost 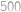 korun v korunových mincích a nic jiného. Z bankomatu se dá buď vybrat přesně
korun v korunových mincích a nic jiného. Z bankomatu se dá buď vybrat přesně 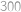 korun (za předpokladu, že v něm alespoň taková hotovost je) nebo do něj vložit přesně
korun (za předpokladu, že v něm alespoň taková hotovost je) nebo do něj vložit přesně 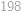 korun. Jakou největší hotovost si mohl Honzík vybrat, pokud u sebe na začátku neměl ani korunu? (Mohl vkládat a vybírat kolikrát chtěl a v libovolném pořadí.)
korun. Jakou největší hotovost si mohl Honzík vybrat, pokud u sebe na začátku neměl ani korunu? (Mohl vkládat a vybírat kolikrát chtěl a v libovolném pořadí.)
Zobraziť / skryť výsledok
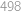 korun.
korun.
Předpokládejme, že během prvních několika kroků (krokem míníme buď vybrání hotovosti z bankomatu nebo její vložení) Honzík celkem  -krát vybral z bankomatu
-krát vybral z bankomatu 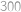 korun a celkem
korun a celkem  -krát vložil
-krát vložil 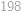 korun. Potom částka, kterou u sebe nakonec měl, byla rovna
korun. Potom částka, kterou u sebe nakonec měl, byla rovna 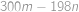 korunám. Protože
korunám. Protože  je (největším) společným dělitelem čísel
je (největším) společným dělitelem čísel 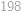 a
a 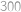 , musela být Honzíkova hotovost v každém okamžiku dělitelná šesti, a tedy nemohla přesáhnout
, musela být Honzíkova hotovost v každém okamžiku dělitelná šesti, a tedy nemohla přesáhnout 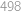 korun.
korun.
Ukážeme, že vybrání částky 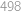 korun bylo možné. Je snadné si uvědomit, že v každém okamžiku mohl Honzík z bankomatu buď vybrat nebo do něj vložit, přičemž obě možnosti přicházely v úvahu jen tehdy, když u sebe měl
korun bylo možné. Je snadné si uvědomit, že v každém okamžiku mohl Honzík z bankomatu buď vybrat nebo do něj vložit, přičemž obě možnosti přicházely v úvahu jen tehdy, když u sebe měl 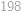 korun. Předpokládejme, že Honzík při vybírání postupoval tak, že pokud u sebe měl
korun. Předpokládejme, že Honzík při vybírání postupoval tak, že pokud u sebe měl 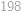 korun, vybral z bankomatu dalších
korun, vybral z bankomatu dalších 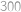 , a ve zbylých případech dělal to, co musel (a pokud měl
, a ve zbylých případech dělal to, co musel (a pokud měl 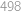 , tak skončil). Nyní si stačí uvědomit (rozmysli si), že během každých pěti po sobě následujících kroků se Honzíkova hotovost zvýšila o šest korun (dvakrát vybral a třikrát vložil), takže se tímto algoritmem postupně dostal až na kýžených
, tak skončil). Nyní si stačí uvědomit (rozmysli si), že během každých pěti po sobě následujících kroků se Honzíkova hotovost zvýšila o šest korun (dvakrát vybral a třikrát vložil), takže se tímto algoritmem postupně dostal až na kýžených 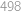 korun.
korun.
Úloha 17
Slepíme tři stejně velké čtverce do tvaru L. Rozdělte tento útvar na osm shodných útvarů.
Zobraziť / skryť výsledok
Zobraziť / skryť riešenie
Úloha 18
Olin dostal na Velikonoce šachovnici 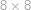 bez pravého horního a levého dolního rohového políčka. Kolika způsoby na ni může postavit osm veží tak, aby se navzájem neohrožovaly?
bez pravého horního a levého dolního rohového políčka. Kolika způsoby na ni může postavit osm veží tak, aby se navzájem neohrožovaly?
Zobraziť / skryť výsledok
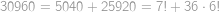 .
.
Aby se věže navzájem neohrožovaly, musí mít každá svůj vlastní sloupec a vlastní řádek (v žádném sloupci či řádku nemohou stát dvě věže). Jelikož je věží osm a šachovnice má pouze osm řádků a osm sloupců, bude v každém řádku a v každém sloupci právě jedna věž. Budeme rozestavovat věže do řádků, přičemž přednostně zaplníme krajní (neúplné) řádky.
Umístíme-li věž v horním řádku do políčka nejvíc vlevo, můžeme v dolním řádku umístit věž do kteréhokoliv políčka — políčko zcela nalevo, které ohrožuje první umístěná věž, na naší šachovnici chybí. Tuto věž tedy můžeme umístit sedmi způsoby. Zbývajících šest věží pak umístíme následovně: v druhém řádku (je jedno, jestli druhý odshora, nebo odspodu) můžeme věž umístit na libovolné z šesti políček (dvě jsou ohrožena již umístěnými věžemi), ve třetím pak vybíráme z pěti políček (tři jsou ohrožena) atd. atd., až poslední věž můžeme umístit pouze na jediné neohrožené políčko. Celkem tedy 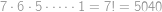 způsobů.
způsobů.
V druhém případě umístíme věž v horním řádku na kterékoliv políčko, jen ne na to nejvíc vlevo (takovýchto políček je šest, jelikož v tomto řádku ještě chybí to nejvíc napravo). Potom můžeme umístit věž ve spodním řádku pouze šesti způsoby, protože ze sedmi políček v tomto řádku je již jedno ohrožené věží nahoře. Zbývajících šest věží umístíme stejně jako v předchozím případě, celkem je tedy v tomto případě 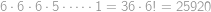 způsobů rozmístění.
způsobů rozmístění.
Shrnutím obou alternativ dostáváme celkový počet způsobů rozmístění věží jako 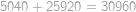 .
.
Úloha 19
Kvadratická rovnice 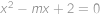 s parametrem
s parametrem  má kořeny
má kořeny  ,
, 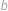 . Předpokládejme, že
. Předpokládejme, že
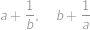
jsou kořeny kvadratické rovnice
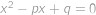 .
. Určete hodnotu
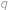
(v závislosti na
 ).
Zobraziť / skryť výsledok
).
Zobraziť / skryť výsledok
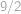 .
.
Úloha 20
Vejtek si vymyslel čtyři kladná, ne nutně celá čísla  ,
, 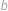 ,
,  a
a 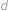 . Potom má šest možností, jak vynásobit právě dvě z nich, konkrétně
. Potom má šest možností, jak vynásobit právě dvě z nich, konkrétně 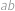 ,
, 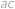 ,
, 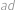 ,
, 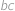 ,
, 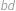 a
a  . Frantovi ale Vejtek řekl pouze pět z těchto šesti součinů, konkrétně
. Frantovi ale Vejtek řekl pouze pět z těchto šesti součinů, konkrétně  ,
,  ,
,  ,
,  a
a  . Pomozte Frantovi najít šestý součin.
. Pomozte Frantovi najít šestý součin.
Zobraziť / skryť výsledok
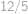 .
.
Všimneme si, že součin 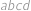 lze dostat násobením čísel
lze dostat násobením čísel 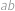 ,
, 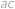 ,
, 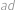 ,
, 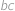 ,
, 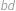 a
a  třemi různými způsoby. Pokud postupně násobíme dvojice z čísel
třemi různými způsoby. Pokud postupně násobíme dvojice z čísel  ,
,  ,
,  ,
,  a
a  , jediné číslo, které se nám vyskytne dvakrát je
, jediné číslo, které se nám vyskytne dvakrát je 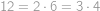 . Proto poslední hledaný součin je
. Proto poslední hledaný součin je 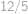 .
.
Úloha 21
V klobouku kouzelníka Pokustóna se krčí  černých a
černých a  bílí králíci. Náhodně z klobouku vytáhneme
bílí králíci. Náhodně z klobouku vytáhneme  králíků. Jaká je pravděpodobnost, že poslední vytažený králík bude černý?
králíků. Jaká je pravděpodobnost, že poslední vytažený králík bude černý?
Zobraziť / skryť výsledok
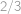 .
.
Uvažme všechna možná pořadí všech dvanácti králíků (králíky stejné barvy nerozlišujeme). Každé z nich má stejnou pravděpodobnost, že právě tak budeme králíky z klobouku tahat (rozmyslete si!). Počet pořadí v nichž je na šestém místě černý králík, je stejný jako počet těch, v nichž je na prvním místě černý králík (stačí ono pořadí posunout o  pozic). Hledaná pravděpodobnost je tedy stejná jako ta, že první vytažený králík bude černé barvy, čili
pozic). Hledaná pravděpodobnost je tedy stejná jako ta, že první vytažený králík bude černé barvy, čili 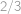 .
.
Úloha 22
Jaký zbytek dostaneme při dělení čísla  dvanácti?
dvanácti?
Zobraziť / skryť výsledok
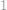 .
.
Úloha 23
Kája má kus dřevěné desky tvaru rovnoramenného pravoúhlého trojúhelníka se stranami délky 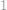 ,
, 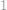 a
a 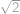 . Chce ho rozříznout jedním řezem na dva kusy se stejným obsahem. Poraďte Káje, kudy vést nejkratší řez (tj. úsečku), a určete jeho délku.
. Chce ho rozříznout jedním řezem na dva kusy se stejným obsahem. Poraďte Káje, kudy vést nejkratší řez (tj. úsečku), a určete jeho délku.
Zobraziť / skryť výsledok
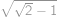 .
.
Úloha 24
Která políčka můžeme ze šachovnice 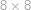 vystřihnout, aby se zbytek dal pokrýt
vystřihnout, aby se zbytek dal pokrýt 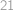 kostičkami tvaru
kostičkami tvaru 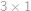 ?
?
Zobraziť / skryť výsledok
Zobraziť / skryť riešenie
Políčka na šachovnici rozdělíme do tří skupin, tak jako na obrázku.
Všimněte si, že každá kostička zaplní právě jedno políčko od každé skupiny. Políček značených číslem
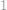
je o jedno více než ostatních, takže vystřihnout musíme jedno takové políčko. Nyní políčka rozdělíme do tří skupin ještě druhým způsobem, a to osově symetricky s prvním rozdělením. V jedné skupině bude opět o políčko více a výběr políček na vystřihnutí se nám zúží na pouhá čtyři políčka. Sami jistě ukážete, že při vystřižení libovolného z nich již lze šachovnici našimi kostičkami pokrýt a úloha je tím pak vyřešena.
Úloha 25
Šavlík s Pepou hrají následující hru. Mají hromádku s  zápalkami a střídají se v tazích. Každý musí ve svém tahu odebrat z hromádky kladný počet zápalek nepřevyšující polovinu zápalek na hromádce. Ten, kdo bude mít na začátku svého tahu jen jednu zápalku (a tedy nebude moci provést svůj tah), vyhraje. Když víte, že Šavlík začíná, najděte
zápalkami a střídají se v tazích. Každý musí ve svém tahu odebrat z hromádky kladný počet zápalek nepřevyšující polovinu zápalek na hromádce. Ten, kdo bude mít na začátku svého tahu jen jednu zápalku (a tedy nebude moci provést svůj tah), vyhraje. Když víte, že Šavlík začíná, najděte  nejblíže k číslu
nejblíže k číslu 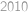 takové, že Pepa může vyhrát (bez ohledu na to, jak dobře hraje Šavlík).
takové, že Pepa může vyhrát (bez ohledu na to, jak dobře hraje Šavlík).
Zobraziť / skryť výsledok
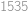 .
.
Úloha 26
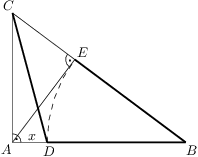
Trojúhelník 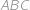 má pravý úhel u vrcholu
má pravý úhel u vrcholu  . Na straně
. Na straně 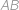 se nachází bod
se nachází bod  , přičemž
, přičemž 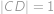 . Dále
. Dále 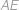 je výška z bodu
je výška z bodu  na stranu
na stranu 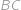 . Najděte délku
. Najděte délku 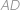 , pokud navíc víte, že
, pokud navíc víte, že 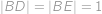 .
.
Zobraziť / skryť výsledok
Zobraziť / skryť riešenie
Označme hledanou délku
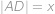 .
. Z Pythagorových vět pro trojúhelníky
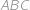
a
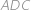
vyjádříme
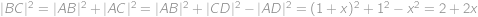 .
. Z podobných trojúhelníků
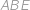 ,
, 
plyne rovnost poměrů
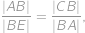
ve které všechny vzdálenosti umíme vyjádřit pomocí
 .
. Po úpravě (mimo jiné krácení nenulovým výrazem
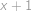 )
) vyjde
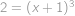 ,
, tedy
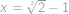 .
.
Úloha 27
Množina 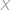 má
má  prvků. Nechť
prvků. Nechť  ,
,  jsou dvě náhodné podmnožiny
jsou dvě náhodné podmnožiny 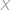 . Jaká je pravděpodobnost, že
. Jaká je pravděpodobnost, že  je podmnožina
je podmnožina  ? Upřesnění: Při náhodném výběru podmnožiny
? Upřesnění: Při náhodném výběru podmnožiny 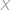 vybereme každou z
vybereme každou z 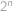 podmnožin se stejnou pravděpodobností (rovnou
podmnožin se stejnou pravděpodobností (rovnou 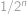 ). Výběry podmnožin
). Výběry podmnožin  a
a  jsou navzájem nezávislé.
jsou navzájem nezávislé.
Zobraziť / skryť výsledok
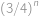 .
.
Vezměme si jeden prvek 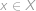 . Pro něj máme čtyři možnosti. Buď (
. Pro něj máme čtyři možnosti. Buď (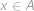 ,
, 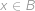 ), nebo (
), nebo (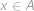 ,
, 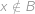 ), nebo (
), nebo (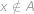 ,
, 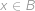 ), nebo (
), nebo (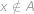 ,
, 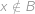 ). Aby platila inkluze
). Aby platila inkluze  , nesmí pro žádný prvek
, nesmí pro žádný prvek 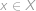 nastat možnost (
nastat možnost (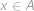 ,
, 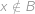 ), čemuž odpovídá pravděpodobnost
), čemuž odpovídá pravděpodobnost 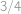 . Tato pravděpodobnost je nezávislá pro všechny prvky
. Tato pravděpodobnost je nezávislá pro všechny prvky 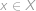 , proto výsledek
, proto výsledek 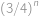 .
.
Úloha 28
Najděte největší přirozené číslo  takové, že rovnice
takové, že rovnice 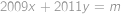 má právě jedno řešení v přirozených číslech(tj. v číslech
má právě jedno řešení v přirozených číslech(tj. v číslech 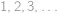 ).
).
Zobraziť / skryť výsledok
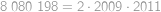 .
.
Úloha 29
Najděte alespoň jedno reálné číslo  , pro které platí
, pro které platí

Zobraziť / skryť výsledok
 .
.
Předpokládejme, že reálné číslo  splňuje
splňuje  . Potom
. Potom
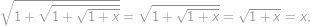
a tedy

je řešením naší úlohy. Pro nezáporné

lze rovnost

ekvivalentně přepsat jako
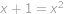 .
. Tato rovnice má nezáporné řešení
 ,
, které je tedy i řešením původní úlohy.
Úloha 30
Najděte všechny dvojice 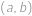 přirozených čísel takové, že
přirozených čísel takové, že 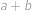 má (v desítkové soustavě) na místě jednotek cifru
má (v desítkové soustavě) na místě jednotek cifru  ,
, 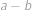 je prvočíslo a
je prvočíslo a 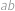 je druhou mocninou přirozeného čísla.
je druhou mocninou přirozeného čísla.
Zobraziť / skryť výsledok
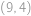 .
.
Pokud mají čísla  ,
, 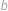 společného dělitele většího než
společného dělitele většího než 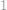 , pak vzhledem k tomu, že
, pak vzhledem k tomu, že 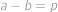 pro nějaké prvočíslo
pro nějaké prvočíslo 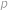 , je tímto dělitelem právě ono prvočíslo. Pak ale musí platit
, je tímto dělitelem právě ono prvočíslo. Pak ale musí platit 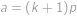 a
a 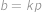 pro nějaké
pro nějaké 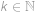 . Dle zadání je
. Dle zadání je 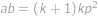 druhou mocninou přirozeného čísla, tedy rovněž
druhou mocninou přirozeného čísla, tedy rovněž 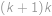 je druhou mocninou přirozeného čísla. Protože čísla
je druhou mocninou přirozeného čísla. Protože čísla 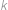 ,
, 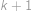 jsou nesoudělná, musí být čtvercem přirozeného čísla každé z nich, což vede ke sporu.
jsou nesoudělná, musí být čtvercem přirozeného čísla každé z nich, což vede ke sporu.
Předpokládejme nyní, že  ,
, 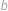 jsou nesoudělná čísla. Jelikož jejich součin je čtverec, musí být
jsou nesoudělná čísla. Jelikož jejich součin je čtverec, musí být 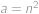 ,
, 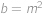 pro nějaká přirozená čísla
pro nějaká přirozená čísla  ,
,  . Máme
. Máme 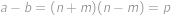 , což vzhledem k tomu, že
, což vzhledem k tomu, že 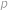 je prvočíslo, dává
je prvočíslo, dává  ,
,  . Odtud dostáváme
. Odtud dostáváme 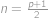 ,
, 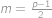 . Tedy
. Tedy
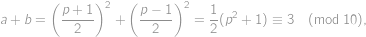
což dává
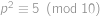 .
. Pak ale

dělí
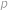 ,
, a protože
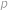
je prvočíslo, musí být
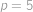 .
. Dosazením do vztahů pro
 ,
, 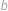
získáme jediné řešení úlohy, a to dvojici
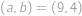 .
.
Úloha 31
Na šachovnici 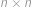 je rozmístěných
je rozmístěných 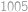 dominových kostiček tak, že každá z nich zakrývá dvě políčka šachovnice sousedící stranou. Žádné dvě dominové kostičky se nepřekrývají ani nedotýkají (a to ani rohem). Najděte nejmenší možné
dominových kostiček tak, že každá z nich zakrývá dvě políčka šachovnice sousedící stranou. Žádné dvě dominové kostičky se nepřekrývají ani nedotýkají (a to ani rohem). Najděte nejmenší možné  , pro které to může platit.
, pro které to může platit.
Zobraziť / skryť výsledok
 .
.
Úloha 32
Nechť 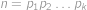 je rozklad čísla
je rozklad čísla  na prvočísla, ne nutně různá. Číslo
na prvočísla, ne nutně různá. Číslo  nazveme zelené, pokud
nazveme zelené, pokud  dělí
dělí 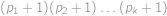 . Nalezněte nejmenší zelené číslo větší než
. Nalezněte nejmenší zelené číslo větší než 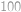 .
.
Zobraziť / skryť výsledok
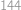 .
.
Úloha 33
Pro každou uspořádanou dvojici přirozených čísel 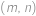 definujeme hodnotu
definujeme hodnotu 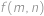 . Víme, že pro všechna
. Víme, že pro všechna  ,
,  přirozená platí
přirozená platí
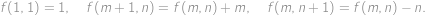
Najděte všechna přirozená čísla
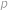 ,
, pro která existuje přirozené číslo
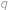
takové, že platí
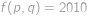 .
Zobraziť / skryť výsledok
.
Zobraziť / skryť výsledok
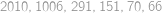 .
.
Postupným zvětšováním  a
a  dostaneme jednoznačný tvar funkce splňující dané podmínky, a to
dostaneme jednoznačný tvar funkce splňující dané podmínky, a to
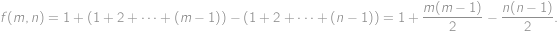
Po dosazení
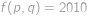
nám stačí zjistit, pro která přirozená
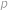 ,
, 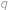
platí vztah (po úpravě)
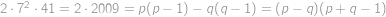 .
. Jelikož však
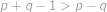 ,
, stačí nám najít všechna přirozená
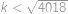
dělící
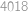 ,
, pro která má soustava
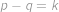
a
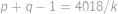
řešení v přirozených číslech. Sečtením obdržíme
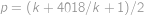 ,
, což je přirozené číslo vždy, neboť čitatel je sudý. Analogicky vyjde i
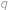
přirozené. Nyní již rutinně pro
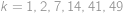
dosadíme a dostaneme
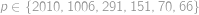 .
.
Úloha 34
Na univerzitě je  studentů. Ví se, že každý učitel učí právě
studentů. Ví se, že každý učitel učí právě 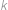 studentů a pro každou dvojici (různých) studentů existuje právě
studentů a pro každou dvojici (různých) studentů existuje právě  učitelů, kteří je učí oba dva. Kolik učitelů je na univerzitě?
učitelů, kteří je učí oba dva. Kolik učitelů je na univerzitě?
Zobraziť / skryť výsledok
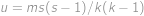 .
.
Úloha 35
V rovině je nakreslených  různých přímek. Když se protnou právě
různých přímek. Když se protnou právě  přímky v jednom bodě, nazveme tento průsečík modrý, když právě tři, nazveme ho červený. Našich
přímky v jednom bodě, nazveme tento průsečík modrý, když právě tři, nazveme ho červený. Našich  přímek umíme rozdělit na tři trojice. Každá přímka z první trojice obsahuje
přímek umíme rozdělit na tři trojice. Každá přímka z první trojice obsahuje  červené a
červené a 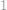 modrý bod, přímky z druhé trojice mají
modrý bod, přímky z druhé trojice mají  červené a
červené a  modré body a každá přímka z třetí trojice má
modré body a každá přímka z třetí trojice má  červené a
červené a  modré body. Určete, na kolik částí dělí těchto
modré body. Určete, na kolik částí dělí těchto  přímek rovinu.
přímek rovinu.
Zobraziť / skryť výsledok
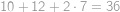 .
.
Úloha 36
Najděte nejmenší reálné číslo 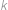 takové, že pro všechna reálná čísla
takové, že pro všechna reálná čísla  ,
, 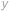 platí
platí 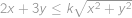 .
.
Zobraziť / skryť výsledok
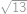 .
.
Volbou 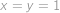 vidíme, že hledané číslo
vidíme, že hledané číslo 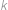 musí být kladné. Dále si rozmyslíme, že stačí, aby nerovnost platila pro všechna kladná čísla
musí být kladné. Dále si rozmyslíme, že stačí, aby nerovnost platila pro všechna kladná čísla  ,
, 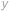 . Přejdeme-li totiž od čísla
. Přejdeme-li totiž od čísla  k číslu
k číslu  , jen zmenšíme levou stranu a nerovnost si tak vlastně zjednodušíme. Pro kladná čísla
, jen zmenšíme levou stranu a nerovnost si tak vlastně zjednodušíme. Pro kladná čísla  ,
, 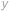 můžeme ekvivalentně umocnit a upravit do tvaru
můžeme ekvivalentně umocnit a upravit do tvaru
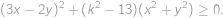
Nyní vidíme, že pokud
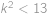 ,
, nerovnost neplatí kdykoliv
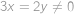 ,
, přičemž pokud
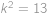 ,
, nerovnost samozřejmě platí. Hledané číslo je tedy
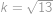 .
.
Úloha 37
Jsou-li  a
a 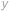 kladná celá čísla splňující
kladná celá čísla splňující 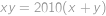 , jaká je potom největší možná hodnota
, jaká je potom největší možná hodnota  ?
?
Zobraziť / skryť výsledok
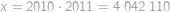 .
.
Převedením na jednu stranu, přičtením  a úpravou na součin získáme rovnici
a úpravou na součin získáme rovnici
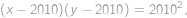
z níž je patrné, že

bude mít největší hodnotu, pokud bude první závorka

a druhá
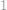 .
. Je tedy
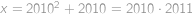 .
.
Úloha 38
Mišo chce nakreslit tabulku velikosti 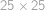 složenou ze
složenou ze 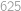 malých čtverečků. Umí ale kreslit jenom čtverce (přesněji jejich obvody) libovolné velikosti. Vždycky kreslí celé čtverce a nemůže používat gumu. Kolik nejméně čtverců musí Mišo nakreslit, aby nakreslil celou tabulku a nic navíc?
malých čtverečků. Umí ale kreslit jenom čtverce (přesněji jejich obvody) libovolné velikosti. Vždycky kreslí celé čtverce a nemůže používat gumu. Kolik nejméně čtverců musí Mišo nakreslit, aby nakreslil celou tabulku a nic navíc?
Zobraziť / skryť výsledok
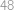 .
.
Úloha 39
Každé políčko šachovnice 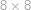 můžeme obarvit bíle nebo černě. Najděte počet různých obarvení takových, že každý čtverec
můžeme obarvit bíle nebo černě. Najděte počet různých obarvení takových, že každý čtverec 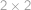 obsahuje dvě bílá a dvě černá políčka.
obsahuje dvě bílá a dvě černá políčka.
Poznámka: Na orientaci šachovnice záleží. Dvě obarvení, která se liší jen otočením či překlopením, považujeme za různá.
Zobraziť / skryť výsledok
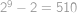 .
.
Úloha 40
Kubická rovnice 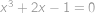 má právě jeden reálný kořen
má právě jeden reálný kořen  . Víme, že
. Víme, že 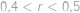 . Najděte všechny rostoucí posloupnosti přirozených čísel
. Najděte všechny rostoucí posloupnosti přirozených čísel 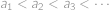 takové, že platí
takové, že platí
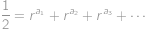
Zobraziť / skryť výsledok
Existuje jen jedna: 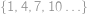 .
.
Dosaďme do dané kubické rovnice  a upravme ji na tvar
a upravme ji na tvar
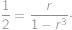
Ze zadání
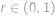 ,
, takže
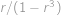
vyjadřuje součet nekonečné geometrické posloupnosti s prvním členem

a s koeficientem
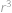 ,
, takže
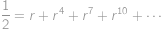
a máme jednu hledanou posloupnost, konkrétně
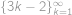 .
. Ukážeme, že toto vyjádření je jednoznačné. Nechť platí
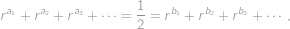
pro dvě různé rostoucí posloupnosti
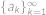 ,
, 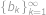
. Označme

nejmenší přirozené číslo takové, že

patří do jedné z těchto posloupností, ale nepatří do druhé. Bez újmy na obecnosti,
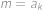
pro nějaké
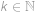
a
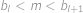
pro nějaké
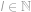 .
. Potom můžeme rovnost
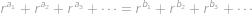
upravit vyškrtnutím stejných členů na tvar
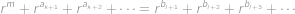
Ukážeme, že pravá strana je ve skutečnosti menší než levá, čímž dojdeme ke sporu. Platí
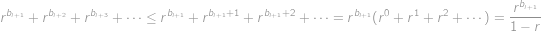
Z nerovností
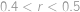
však lehce dostaneme
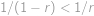 ,
, proto
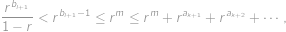
čímž jsme získali spor a tím i dokázali jednoznačnost.
Úloha 41
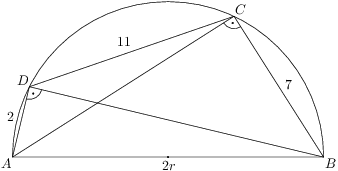
Konvexní šestiúhelník se stranami délek  ,
,  ,
, 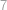 ,
, 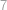 ,
,  a
a  je vepsaný do kružnice. Najděte její poloměr.
je vepsaný do kružnice. Najděte její poloměr.
Zobraziť / skryť výsledok
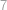 .
.
Hledaný poloměr  je stejný jako poloměr kružnice opsané tětivovému čtyřúhelníku
je stejný jako poloměr kružnice opsané tětivovému čtyřúhelníku 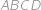 , ve kterém
, ve kterém 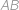 je průměr,
je průměr, 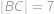 ,
, 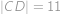 a
a 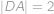 .
.
Z Pythagorových vět vyjádříme pomocí

délky úhlopříček
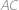
a
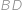 .
. Podle Ptolemaiovy věty pro čtyřúhelník
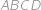
musí platit
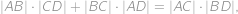
takže
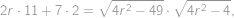
z čehož po umocnění na druhou, roznásobení a vydělení nenulovým

vyjde rovnice
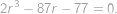
Tipneme si kořen
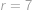
a rozložíme na součin
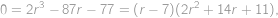
ve kterém je druhá závorka pro
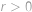
kladná. Jediné řešení je tedy
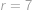 .
.
Úloha 42
V krabici je několik barevných míčků, přičemž od každé barvy jich tam je stejný počet. Pokud do krabice přidáme 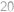 míčků, které mají všechny stejnou barvu, ale různou od všech, které byly předtím v krabici, nezměníme tím pravděpodobnost, že při tahání dvou míčků bez vracení vytáhneme míčky stejné barvy. Kolik míčků bylo na začátku v krabici?
míčků, které mají všechny stejnou barvu, ale různou od všech, které byly předtím v krabici, nezměníme tím pravděpodobnost, že při tahání dvou míčků bez vracení vytáhneme míčky stejné barvy. Kolik míčků bylo na začátku v krabici?
Zobraziť / skryť výsledok
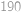 .
.
Předpokládejme, že na začátku jsou v krabici míčky  barev a od každé barvy jich tam je právě
barev a od každé barvy jich tam je právě  . Dva míčky můžeme vytáhnout
. Dva míčky můžeme vytáhnout 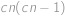 způsoby, dva míčky stejné barvy
způsoby, dva míčky stejné barvy 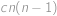 způsoby. Pravděpodobnost, že vytáhneme dva míčky stejné barvy, je tedy
způsoby. Pravděpodobnost, že vytáhneme dva míčky stejné barvy, je tedy 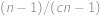 .
.
Přidejme do krabice 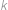 nových míčků v barvě, kterou neměl žádný z míčků, jež tam byly původně (v našem případě je
nových míčků v barvě, kterou neměl žádný z míčků, jež tam byly původně (v našem případě je 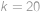 ). Počet způsobů, jak vytáhnout dva míčky, je nyní roven
). Počet způsobů, jak vytáhnout dva míčky, je nyní roven 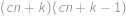 , dva míčky stejné barvy můžeme vytáhnout
, dva míčky stejné barvy můžeme vytáhnout 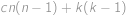 způsoby. Pravděpodobnost vytáhnutí dvou míčků stejné barvy je proto rovna
způsoby. Pravděpodobnost vytáhnutí dvou míčků stejné barvy je proto rovna
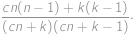
Protože obě pravděpodobnosti se mají rovnat, dostáváme
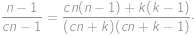
Po roznásobení se většina členů odečte a rovnost nabude tvar
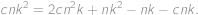
Vydělením nenulovým výrazem

a převedením několika členů na opačnou stranu rovnice získáme
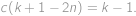
Dosaďme nyní
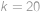 .
. Máme
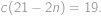
Tato rovnice má v přirozených číslech dvě řešení,
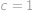 ,
, 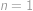
a
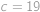 ,
, 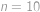
. První řešení ale zjevně nevyhovuje zadání (vyšlo nám proto, že ve vzorci pro pravděpodobnost jsme dělili výrazem
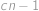 ).
). Snadno nahlédneme, že druhé řešení podmínky zadání splňuje, a tedy dostáváme, že na začátku bylo v krabici
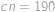
míčků.
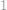 ,
, ,
, 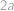 má povrch
má povrch 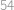 .
. .
.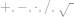 vytvořte číslo
vytvořte číslo  .
. ,
,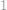 ,
,  ,
, ,
,  Afro mu z ní jeden list vytrhnul. Teď je součet čísel na zbylých listech
Afro mu z ní jeden list vytrhnul. Teď je součet čísel na zbylých listech 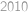 .
.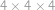 .
.
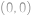 .
.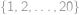 takových, že součin jejich prvků je dělitelný čtyřmi?
takových, že součin jejich prvků je dělitelný čtyřmi?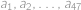 je součet členů s lichými indexy rovný
je součet členů s lichými indexy rovný 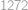 .
.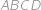 (se základnami
(se základnami 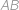 a
a  )
)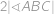 =
= 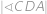 .
.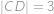 cm a
cm a 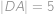 cm. Zjistěte velikost úsečky
cm. Zjistěte velikost úsečky 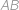 .
.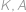 a
a 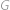 obíhají kolem hvězdy
obíhají kolem hvězdy 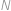 po soustředných kružnicových dráhách (společný střed kružnic je hvězda
po soustředných kružnicových dráhách (společný střed kružnic je hvězda 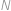 ).
).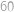 ,
,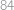 a
a 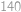 roků. Jednou se stalo, že tyto tři planety spolu s hvězdou
roků. Jednou se stalo, že tyto tři planety spolu s hvězdou 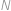 ležely na jedné přímce. Kolik nejméně roků musí uplynout, aby
ležely na jedné přímce. Kolik nejméně roků musí uplynout, aby 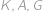 a
a 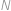 znovu ležely na jedné přímce?
znovu ležely na jedné přímce?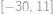 a vydala sa po přímce až do bodu
a vydala sa po přímce až do bodu 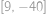 .
. takové, že čísla
takové, že čísla  ,
, mají obě ciferný součet dělitelný číslem
mají obě ciferný součet dělitelný číslem 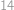 .
. .
.
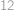 různých hráčů sestavit tři týmy po čtyřech hráčích?
různých hráčů sestavit tři týmy po čtyřech hráčích? .
. km/h, po rovině rychlostí
km/h, po rovině rychlostí  km/h a do kopce rychlostí
km/h a do kopce rychlostí 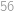 km/h. Cesta z města
km/h. Cesta z města  do města
do města  trvá
trvá  hodiny. Zpáteční cesta trvá
hodiny. Zpáteční cesta trvá  hodiny a
hodiny a 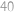 minut. Jaká je vzdálenost po cestě mezi městy
minut. Jaká je vzdálenost po cestě mezi městy  a
a  ?
?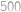 korun v korunových mincích a nic jiného. Z bankomatu se dá buď vybrat přesně
korun v korunových mincích a nic jiného. Z bankomatu se dá buď vybrat přesně 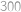 korun (za předpokladu, že v něm alespoň taková hotovost je) nebo do něj vložit přesně
korun (za předpokladu, že v něm alespoň taková hotovost je) nebo do něj vložit přesně 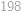 korun. Jakou největší hotovost si mohl Honzík vybrat, pokud u sebe na začátku neměl ani korunu? (Mohl vkládat a vybírat kolikrát chtěl a v libovolném pořadí.)
korun. Jakou největší hotovost si mohl Honzík vybrat, pokud u sebe na začátku neměl ani korunu? (Mohl vkládat a vybírat kolikrát chtěl a v libovolném pořadí.)
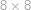 bez pravého horního a levého dolního rohového políčka. Kolika způsoby na ni může postavit osm veží tak, aby se navzájem neohrožovaly?
bez pravého horního a levého dolního rohového políčka. Kolika způsoby na ni může postavit osm veží tak, aby se navzájem neohrožovaly?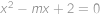 s parametrem
s parametrem  má kořeny
má kořeny  ,
,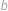 . Předpokládejme, že
. Předpokládejme, že 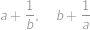
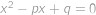 .
.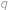 (v závislosti na
(v závislosti na  ).
). ,
,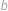 ,
,  a
a 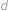 .
.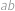 ,
,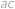 ,
, 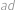 ,
,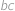 ,
, 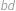 a
a  .
. ,
, ,
,  ,
, a
a  .
. černých a
černých a  bílí králíci. Náhodně z klobouku vytáhneme
bílí králíci. Náhodně z klobouku vytáhneme  králíků. Jaká je pravděpodobnost, že poslední vytažený králík bude černý?
králíků. Jaká je pravděpodobnost, že poslední vytažený králík bude černý? dvanácti?
dvanácti?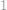 ,
,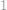 a
a 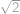 .
.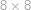 vystřihnout, aby se zbytek dal pokrýt
vystřihnout, aby se zbytek dal pokrýt 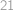 kostičkami tvaru
kostičkami tvaru 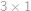 ?
? zápalkami a střídají se v tazích. Každý musí ve svém tahu odebrat z hromádky kladný počet zápalek nepřevyšující polovinu zápalek na hromádce. Ten, kdo bude mít na začátku svého tahu jen jednu zápalku (a tedy nebude moci provést svůj tah), vyhraje. Když víte, že Šavlík začíná, najděte
zápalkami a střídají se v tazích. Každý musí ve svém tahu odebrat z hromádky kladný počet zápalek nepřevyšující polovinu zápalek na hromádce. Ten, kdo bude mít na začátku svého tahu jen jednu zápalku (a tedy nebude moci provést svůj tah), vyhraje. Když víte, že Šavlík začíná, najděte  nejblíže k číslu
nejblíže k číslu 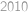 takové, že Pepa může vyhrát (bez ohledu na to, jak dobře hraje Šavlík).
takové, že Pepa může vyhrát (bez ohledu na to, jak dobře hraje Šavlík).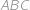 má pravý úhel u vrcholu
má pravý úhel u vrcholu  .
.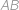 se nachází bod
se nachází bod  ,
,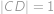 .
.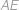 je výška z bodu
je výška z bodu  na stranu
na stranu 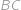 .
.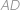 ,
,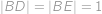 .
.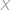 má
má  prvků. Nechť
prvků. Nechť  ,
, jsou dvě náhodné podmnožiny
jsou dvě náhodné podmnožiny 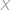 .
. je podmnožina
je podmnožina  ?
?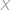 vybereme každou z
vybereme každou z 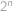 podmnožin se stejnou pravděpodobností (rovnou
podmnožin se stejnou pravděpodobností (rovnou 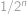 ).
). a
a  jsou navzájem nezávislé.
jsou navzájem nezávislé. takové, že rovnice
takové, že rovnice 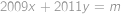 má právě jedno řešení v přirozených číslech(tj. v číslech
má právě jedno řešení v přirozených číslech(tj. v číslech 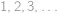 ).
). ,
,
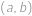 přirozených čísel takové, že
přirozených čísel takové, že 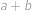 má (v desítkové soustavě) na místě jednotek cifru
má (v desítkové soustavě) na místě jednotek cifru  ,
,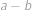 je prvočíslo a
je prvočíslo a 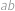 je druhou mocninou přirozeného čísla.
je druhou mocninou přirozeného čísla.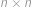 je rozmístěných
je rozmístěných 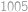 dominových kostiček tak, že každá z nich zakrývá dvě políčka šachovnice sousedící stranou. Žádné dvě dominové kostičky se nepřekrývají ani nedotýkají (a to ani rohem). Najděte nejmenší možné
dominových kostiček tak, že každá z nich zakrývá dvě políčka šachovnice sousedící stranou. Žádné dvě dominové kostičky se nepřekrývají ani nedotýkají (a to ani rohem). Najděte nejmenší možné  ,
,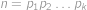 je rozklad čísla
je rozklad čísla  na prvočísla, ne nutně různá. Číslo
na prvočísla, ne nutně různá. Číslo  nazveme zelené, pokud
nazveme zelené, pokud  dělí
dělí 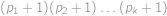 .
.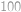 .
.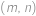 definujeme hodnotu
definujeme hodnotu 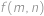 .
. ,
, přirozená platí
přirozená platí 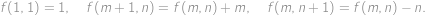
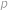 ,
,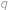 takové, že platí
takové, že platí 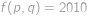 .
. studentů. Ví se, že každý učitel učí právě
studentů. Ví se, že každý učitel učí právě 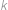 studentů a pro každou dvojici (různých) studentů existuje právě
studentů a pro každou dvojici (různých) studentů existuje právě  učitelů, kteří je učí oba dva. Kolik učitelů je na univerzitě?
učitelů, kteří je učí oba dva. Kolik učitelů je na univerzitě? různých přímek. Když se protnou právě
různých přímek. Když se protnou právě  přímky v jednom bodě, nazveme tento průsečík modrý, když právě tři, nazveme ho červený. Našich
přímky v jednom bodě, nazveme tento průsečík modrý, když právě tři, nazveme ho červený. Našich  přímek umíme rozdělit na tři trojice. Každá přímka z první trojice obsahuje
přímek umíme rozdělit na tři trojice. Každá přímka z první trojice obsahuje  červené a
červené a 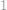 modrý bod, přímky z druhé trojice mají
modrý bod, přímky z druhé trojice mají  červené a
červené a  modré body a každá přímka z třetí trojice má
modré body a každá přímka z třetí trojice má  červené a
červené a  modré body. Určete, na kolik částí dělí těchto
modré body. Určete, na kolik částí dělí těchto  přímek rovinu.
přímek rovinu.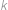 takové, že pro všechna reálná čísla
takové, že pro všechna reálná čísla  ,
,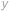 platí
platí 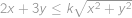 .
. a
a 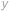 kladná celá čísla splňující
kladná celá čísla splňující 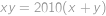 ,
, ?
?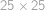 složenou ze
složenou ze 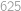 malých čtverečků. Umí ale kreslit jenom čtverce (přesněji jejich obvody) libovolné velikosti. Vždycky kreslí celé čtverce a nemůže používat gumu. Kolik nejméně čtverců musí Mišo nakreslit, aby nakreslil celou tabulku a nic navíc?
malých čtverečků. Umí ale kreslit jenom čtverce (přesněji jejich obvody) libovolné velikosti. Vždycky kreslí celé čtverce a nemůže používat gumu. Kolik nejméně čtverců musí Mišo nakreslit, aby nakreslil celou tabulku a nic navíc?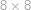 můžeme obarvit bíle nebo černě. Najděte počet různých obarvení takových, že každý čtverec
můžeme obarvit bíle nebo černě. Najděte počet různých obarvení takových, že každý čtverec 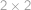 obsahuje dvě bílá a dvě černá políčka.
obsahuje dvě bílá a dvě černá políčka. 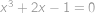 má právě jeden reálný kořen
má právě jeden reálný kořen  .
.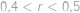 .
.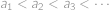 takové, že platí
takové, že platí 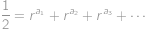
 ,
, ,
, 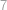 ,
,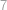 ,
,  a
a  je vepsaný do kružnice. Najděte její poloměr.
je vepsaný do kružnice. Najděte její poloměr.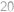 míčků, které mají všechny stejnou barvu, ale různou od všech, které byly předtím v krabici, nezměníme tím pravděpodobnost, že při tahání dvou míčků bez vracení vytáhneme míčky stejné barvy. Kolik míčků bylo na začátku v krabici?
míčků, které mají všechny stejnou barvu, ale různou od všech, které byly předtím v krabici, nezměníme tím pravděpodobnost, že při tahání dvou míčků bez vracení vytáhneme míčky stejné barvy. Kolik míčků bylo na začátku v krabici?
 je
je 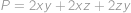 .
.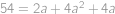 můžeme ještě zkrátit dvojkou a dostaneme kvadratickou rovnici
můžeme ještě zkrátit dvojkou a dostaneme kvadratickou rovnici 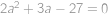 .
.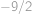 .
.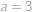 .
.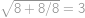 .
.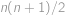 (jde o aritmetickou posloupnost). Číslo chybějícího listu označíme
(jde o aritmetickou posloupnost). Číslo chybějícího listu označíme 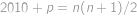 .
.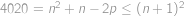 (ze zadání víme
(ze zadání víme 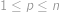 ).
).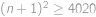 .
.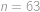 a pro toto
a pro toto 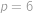 .
.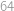 a víc, vyjde nám
a víc, vyjde nám  ,
,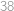 .
.
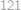 .
.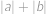 .
.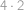 bodů, ve vzdálenosti 4 je
bodů, ve vzdálenosti 4 je 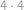 bodů,
bodů,  ,
,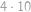 a počátek je jeden.
a počátek je jeden.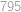 .
.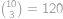 ),
),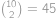 způsoby) a jednoho čísla z množiny
způsoby) a jednoho čísla z množiny 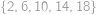 ,
,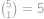 způsoby. Dohromady
způsoby. Dohromady 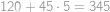 trojic má součin nedělitelný
trojic má součin nedělitelný 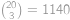 ,
,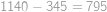 .
.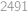 .
.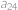 a diference
a diference 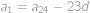 ,
, . Nyní vidíme, že součet všech členů s lichými indexy je
. Nyní vidíme, že součet všech členů s lichými indexy je 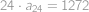 ,
,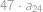 ,
,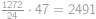 .
.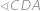 a označme
a označme 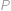 její průsečík se stranou
její průsečík se stranou 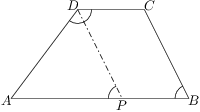
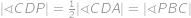 ,
,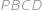 rovnoběžník a
rovnoběžník a 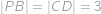 cm.
cm.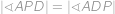 je trojúhelník
je trojúhelník 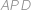 rovnoramenný (se základnou
rovnoramenný (se základnou 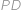 ),
),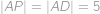 cm.
cm.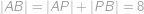 cm.
cm.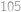 roků.
roků.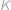 a
a 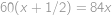 ,
,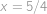 .
.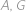 a
a 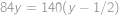 a řešení
a řešení 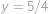 .
.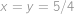 ,
,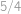 své dráhy, což je
své dráhy, což je 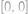 .
.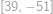 .
.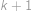 stejně dlouhých úseků, a Monča by po cestě potkala celkem
stejně dlouhých úseků, a Monča by po cestě potkala celkem 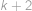 mřížových bodů (počítáno i s krajními), tedy
mřížových bodů (počítáno i s krajními), tedy 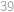 i
i 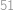 .
.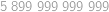 .
.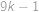 .
.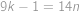 pro
pro 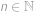 .
.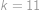 ,
,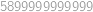 .
.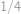 .
.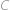 je jeho bod dotyku s poloměrem půlkruhu,
je jeho bod dotyku s poloměrem půlkruhu, 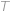 je bod dotyku půlkruhu a malého kruhu a
je bod dotyku půlkruhu a malého kruhu a 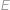 je pata kolmice z
je pata kolmice z 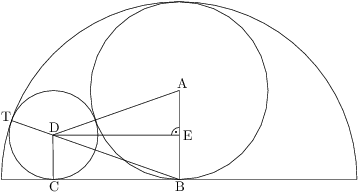
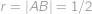 ,
,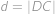 .
.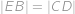 ,
,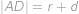 ,
, 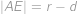 ,
,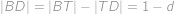 . Trojúhelník
. Trojúhelník 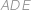 je pravoúhlý (s pravým úhlem u
je pravoúhlý (s pravým úhlem u  .
.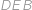 je rovněž pravoúhlý (s pravým úhlem u
je rovněž pravoúhlý (s pravým úhlem u  .
.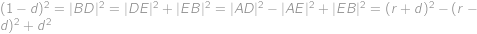 .
.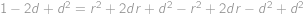 a po odečtení:
a po odečtení: 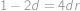 .
.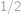 ), tedy
), tedy 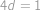 ,
,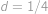 .
.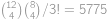 .
.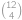 způsoby. Do druhého pak vybíráme ze zbylých
způsoby. Do druhého pak vybíráme ze zbylých 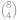 způsobů. Zbylí hráči budou ve třetím týmu. Protože týmy jsou od sebe nerozlišitelné, musíme celkový výsledek vydělit číslem
způsobů. Zbylí hráči budou ve třetím týmu. Protože týmy jsou od sebe nerozlišitelné, musíme celkový výsledek vydělit číslem 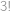 .
.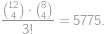
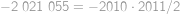 .
.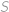 hledaný součet. Členy řady „chytře“ uzávorkujeme a použijeme vzorec pro rozdíl druhých mocnin:
hledaný součet. Členy řady „chytře“ uzávorkujeme a použijeme vzorec pro rozdíl druhých mocnin: 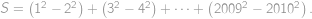
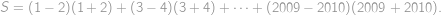
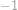 .
.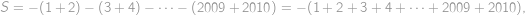
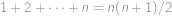 .
.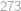 km.
km.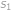 ,
,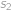 resp.
resp. 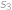 vzdálenosti, které je při cestě z
vzdálenosti, které je při cestě z 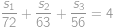
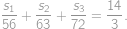
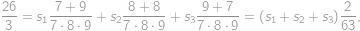
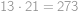 km.
km.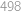 korun.
korun.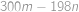 korunám. Protože
korunám. Protože 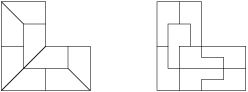
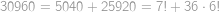 .
.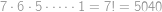 způsobů.
způsobů. 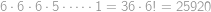 způsobů rozmístění.
způsobů rozmístění. 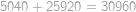 .
.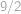 .
.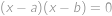 ,
,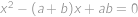 .
.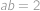 a
a 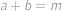 .
.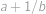 a
a 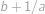 ,
,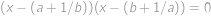 .
.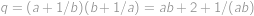 .
.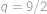 .
.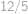 .
.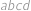 lze dostat násobením čísel
lze dostat násobením čísel 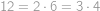 .
.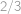 .
.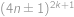 pomocí binomické věty. Tyto zbytky jsou střídavě
pomocí binomické věty. Tyto zbytky jsou střídavě 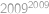 ),
),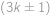 umocněná na
umocněná na 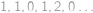 .
.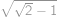 .
.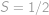 ,
, ,
,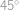 ,
,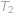 s jedním vrcholem při pravém úhlu. Označíme-li strany trojúhelníka
s jedním vrcholem při pravém úhlu. Označíme-li strany trojúhelníka 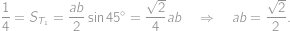
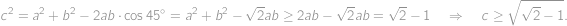
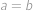 nastává rovnost, umíme dosáhnout řezu s
nastává rovnost, umíme dosáhnout řezu s  .
. a
a  .
.
 .
.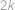 jsou vyhrávající — lze jedním tahem dostat protivníka do prohrávající pozice
jsou vyhrávající — lze jedním tahem dostat protivníka do prohrávající pozice 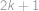 je prohrávající, protože všechny tahy vedou do vyhrávajících pozic. Máme tedy posloupnost prohrávajících pozic definovanou rekurentně jako
je prohrávající, protože všechny tahy vedou do vyhrávajících pozic. Máme tedy posloupnost prohrávajících pozic definovanou rekurentně jako 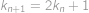 a víme, že první prohrávající pozice je
a víme, že první prohrávající pozice je 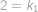 .
.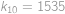 a
a 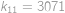 .
.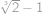
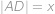 .
.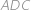 vyjádříme
vyjádříme 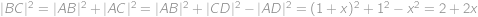 .
.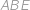 ,
, plyne rovnost poměrů
plyne rovnost poměrů 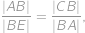
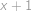 )
)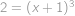 ,
,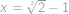 .
.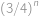 .
.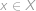 .
.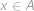 ,
, 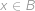 ),
),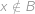 ),
),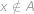 ,
,  ,
,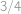 .
.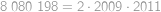 .
.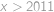 ,
,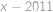 ,
,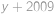 je řešením. Obdobně pokud
je řešením. Obdobně pokud 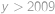 tak i
tak i 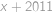 ,
,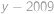 je řešením rovnice. Nyní si stačí rozmyslet, že pro
je řešením rovnice. Nyní si stačí rozmyslet, že pro 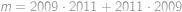 má rovnice jen jedno řešení díky tomu, že
má rovnice jen jedno řešení díky tomu, že 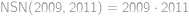 .
. .
. .
.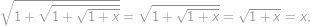
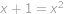 .
.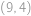 .
.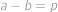 pro nějaké prvočíslo
pro nějaké prvočíslo 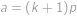 a
a 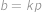 pro nějaké
pro nějaké 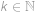 .
.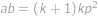 druhou mocninou přirozeného čísla, tedy rovněž
druhou mocninou přirozeného čísla, tedy rovněž 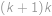 je druhou mocninou přirozeného čísla. Protože čísla
je druhou mocninou přirozeného čísla. Protože čísla 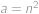 ,
,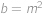 pro nějaká přirozená čísla
pro nějaká přirozená čísla 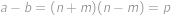 ,
, ,
, . Odtud dostáváme
. Odtud dostáváme 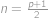 ,
,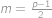 . Tedy
. Tedy 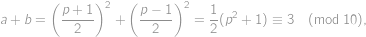
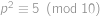 .
.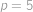 .
.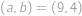 .
. .
.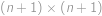 přidáním jednoho sloupce vpravo a jednoho řádku nahoru. Každé dominové kostičce přiřadíme její stín jako na obrázku (stín je tedy obdélník
přidáním jednoho sloupce vpravo a jednoho řádku nahoru. Každé dominové kostičce přiřadíme její stín jako na obrázku (stín je tedy obdélník 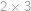 resp.
resp. 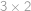 ).
).
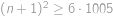 .
.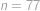 .
. kostiček, což dává dohromady dokonce
kostiček, což dává dohromady dokonce 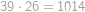 kostiček.
kostiček.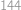 .
.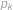 ,
,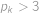 ostře menší než
ostře menší než 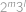 ,
, .
.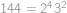 .
.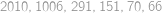 .
.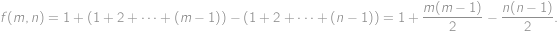
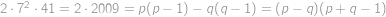 .
.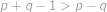 ,
,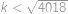 dělící
dělící 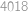 ,
,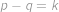 a
a 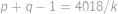 řešení v přirozených číslech. Sečtením obdržíme
řešení v přirozených číslech. Sečtením obdržíme 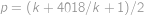 ,
,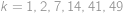 dosadíme a dostaneme
dosadíme a dostaneme 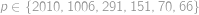 .
.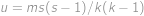 .
. učitelů učí
učitelů učí 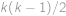 dvojic studentů, takže
dvojic studentů, takže 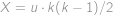 .
.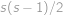 )
)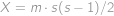 .
.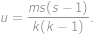
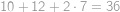 .
.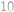 kuliček bude padat do nekonečna, u každého modrého bodu se zastaví právě jedna kulička a u každého červeného dvě kuličky. Stačí tedy už jen dopočítat, že modrých bodů je
kuliček bude padat do nekonečna, u každého modrého bodu se zastaví právě jedna kulička a u každého červeného dvě kuličky. Stačí tedy už jen dopočítat, že modrých bodů je 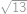 .
.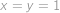 vidíme, že hledané číslo
vidíme, že hledané číslo  ,
,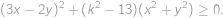
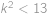 ,
,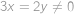 ,
,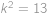 ,
,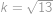 .
.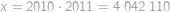 .
. a úpravou na součin získáme rovnici
a úpravou na součin získáme rovnici 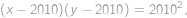
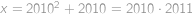 .
.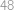 .
.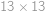 ,
,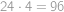 .
.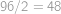 čtverců.
čtverců.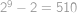 .
.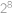 možností.
možností. 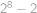 (dvě obarvení na střídačku jsme rozebrali v předchozím bodě).
(dvě obarvení na střídačku jsme rozebrali v předchozím bodě). 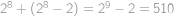 .
.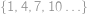 .
.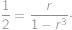
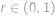 ,
,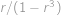 vyjadřuje součet nekonečné geometrické posloupnosti s prvním členem
vyjadřuje součet nekonečné geometrické posloupnosti s prvním členem 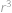 ,
,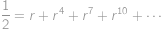
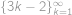 .
.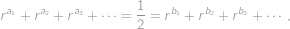
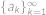 ,
,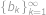 . Označme
. Označme 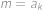 pro nějaké
pro nějaké 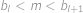 pro nějaké
pro nějaké 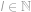 .
.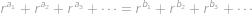
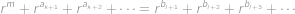
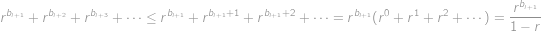
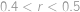 však lehce dostaneme
však lehce dostaneme 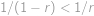 ,
,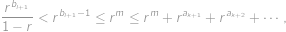
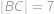 ,
,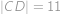 a
a 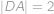 .
.
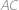 a
a 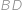 .
.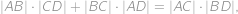
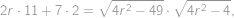
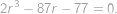
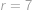 a rozložíme na součin
a rozložíme na součin 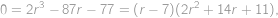
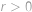 kladná. Jediné řešení je tedy
kladná. Jediné řešení je tedy 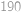 .
.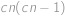 způsoby, dva míčky stejné barvy
způsoby, dva míčky stejné barvy 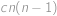 způsoby. Pravděpodobnost, že vytáhneme dva míčky stejné barvy, je tedy
způsoby. Pravděpodobnost, že vytáhneme dva míčky stejné barvy, je tedy 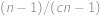 .
.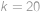 ).
).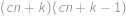 ,
,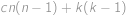 způsoby. Pravděpodobnost vytáhnutí dvou míčků stejné barvy je proto rovna
způsoby. Pravděpodobnost vytáhnutí dvou míčků stejné barvy je proto rovna 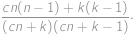
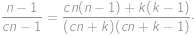
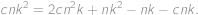
 a převedením několika členů na opačnou stranu rovnice získáme
a převedením několika členů na opačnou stranu rovnice získáme 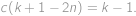
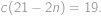
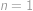 a
a 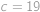 ,
,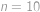 . První řešení ale zjevně nevyhovuje zadání (vyšlo nám proto, že ve vzorci pro pravděpodobnost jsme dělili výrazem
. První řešení ale zjevně nevyhovuje zadání (vyšlo nám proto, že ve vzorci pro pravděpodobnost jsme dělili výrazem 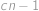 ).
).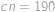 míčků.
míčků.




















