Ülesanne 1
V Americe se pro měření teploty používají místo Celsiových stupňů stupně Fahrenheitovy. Přepočet z Celsiových stupňů na Fahrenheitovy lze provést podle vzorce 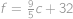 (
( jsou stupně Celsiovy,
jsou stupně Celsiovy, 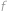 Farenheitovy). Jakou teplotu vyjádří Evropan i Američan stejnou hodnotou?
Farenheitovy). Jakou teplotu vyjádří Evropan i Američan stejnou hodnotou?
Peida / näita vastust
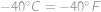 .
.
Ülesanne 2
Nalezněte všechny dvojice reálných čísel 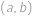 takové, že čísla
takové, že čísla 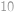 ,
,  ,
, 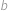 ,
, 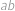 tvoří v tomto pořadí aritmetickou posloupnost.
tvoří v tomto pořadí aritmetickou posloupnost.
Peida / näita vastust
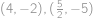 .
.
V aritmetické posloupnosti platí, že každý člen je aritmetickým průměrem členů sousedních. Sestavíme tedy příslušné rovnice
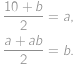
Tato soustava má dvě řešení
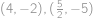 ,
, která obě vyhovují zadání.
Ülesanne 3
Miloš dostal na zkoušce z Esperanta 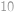 otázek, na které lze odpovídat pouze ANO nebo NE. Test je připraven natolik fikaně, že odpoví-li Miloš na libovolných pět otázek ANO a na zbylých pět otázek NE, bude mít vždy alespoň čtyři správné odpovědi. Zjistěte, kolika způsoby lze takovýto test připravit.
otázek, na které lze odpovídat pouze ANO nebo NE. Test je připraven natolik fikaně, že odpoví-li Miloš na libovolných pět otázek ANO a na zbylých pět otázek NE, bude mít vždy alespoň čtyři správné odpovědi. Zjistěte, kolika způsoby lze takovýto test připravit.
Peida / näita vastust
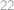 .
.
Jistota čtyř správných odpovědí znamená, že je buď aspoň devět odpovědí ANO nebo aspoň devět odpovědí NE. Možností, jak dát za sebe devětkrát ANO a jednou NE, je 10, analogicky je 10 možností s devíti NE. Ještě musíme připočíst možnost všech desíti ANO a možnost všech desíti NE. Dohromady 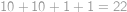 .
.
Ülesanne 4
Najděte nejmenší možnou hodnotu parametru  tak, aby nerovnice
tak, aby nerovnice 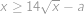 platila pro všechna nezáporná čísla
platila pro všechna nezáporná čísla  .
.
Peida / näita vastust
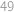 .
.
Ülesanne 5
Mějme krychli a uvažujme všechny trojúhelníky s vrcholy ve vrcholech krychle. Kolik různých vnitřních úhlů se v těchto trojúhelnících objeví?
Peida / näita vastust
 .
.
Ülesanne 6
Kolika způsoby lze seřadit čísla 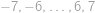 tak, aby absolutní hodnota čísel v seřazené posloupnosti byla neklesající?
tak, aby absolutní hodnota čísel v seřazené posloupnosti byla neklesající?
Peida / näita vastust
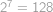 .
.
Ülesanne 7
ABCDEF je pravidelný osmistěn o straně  tvořený čtyřbokými jehlany
tvořený čtyřbokými jehlany 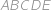 a
a 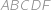 . Určete obsah čtyřúhelníku
. Určete obsah čtyřúhelníku  .
.
Peida / näita vastust
 .
.
Ülesanne 8
Do políček tabulky 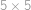 jsou po řádcích (a v rámci řádku zleva doprava) vepsána čísla
jsou po řádcích (a v rámci řádku zleva doprava) vepsána čísla 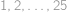 v tomto pořadí. Vybereme pět políček tak, aby žádná dvě nebyla ve stejném řádku ani ve stejném sloupci, a čísla na těchto políčkách sečteme. Jaké hodnoty součtu můžeme tímto způsobem dostat?
v tomto pořadí. Vybereme pět políček tak, aby žádná dvě nebyla ve stejném řádku ani ve stejném sloupci, a čísla na těchto políčkách sečteme. Jaké hodnoty součtu můžeme tímto způsobem dostat?
Peida / näita vastust
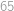 .
.
Ülesanne 9
Vypočítejte 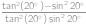 .
.
Peida / näita vastust
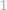 .
.
Zlomek rozšíříme výrazem 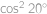 a pak upravíme
a pak upravíme
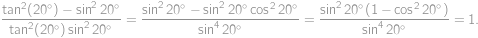
Ülesanne 10
Káťa našla 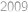 po sobě jdoucích přirozených čísel, která měla stejný součet jako
po sobě jdoucích přirozených čísel, která měla stejný součet jako 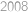 po nich následujících čísel. Které z Kátiných čísel bylo nejmenší?
po nich následujících čísel. Které z Kátiných čísel bylo nejmenší?
Peida / näita vastust
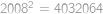 .
.
Ülesanne 11
Kterému celému číslu je roven součin
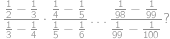
Peida / näita vastust
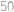 .
.
Označme hledaný součet 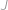 . Stačí převést rozdíly na společné jmenovatele a dostaneme:
. Stačí převést rozdíly na společné jmenovatele a dostaneme:
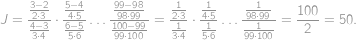
Ülesanne 12
Buď  reálné číslo a
reálné číslo a 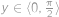 splňující rovnice
splňující rovnice
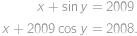
Určete součet
 .
Peida / näita vastust
.
Peida / näita vastust
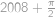 .
.
Ülesanne 13
Mějme posloupnost čísel, pro kterou platí 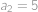 a
a 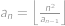 pro
pro 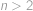 . Zjistěte hodnotu
. Zjistěte hodnotu 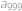 . Výraz
. Výraz 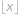 značí největší celé číslo, které nepřesahuje
značí největší celé číslo, které nepřesahuje  .
.
Peida / näita vastust
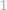 .
.
Ülesanne 14
Pro která přirozená čísla  není
není  násobkem
násobkem 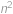 ?
?
Peida / näita vastust
Pro prvočísla a číslo  .
.
Ülesanne 15
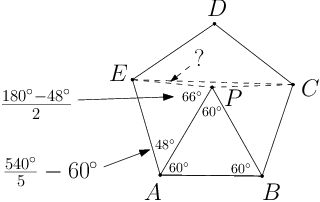
Mějme pravidelný pětiúhelník 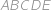 . Sestrojme rovnostranný trojúhelník
. Sestrojme rovnostranný trojúhelník 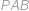 tak, aby bod
tak, aby bod 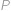 ležel uvnitř pětiúhelníka. Kolik stupňů má úhel
ležel uvnitř pětiúhelníka. Kolik stupňů má úhel 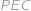 ?
?
Peida / näita vastust
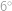 .
.
Některé úhly dopočítáme podle obrázku (využíváme rovnoramennost trojúhelníků a fakt, že vnitřní úhel v pětiúhelníku je 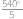 ).
).
Pro další úhly pak platí
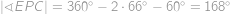
a z rovnoramennosti trojúhelníku
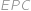
už lehko dopočteme
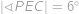 .
.
Ülesanne 16
Nalezněte všechna reálná řešení rovnice

Peida / näita vastust
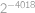 .
.
K oběma stranám rovnice přičteme 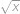 a začneme postupně umocňovat (vždy se některé členy odečtou, díky čemuž lze stále v umocňování pokračovat), až se dostaneme k rovnici
a začneme postupně umocňovat (vždy se některé členy odečtou, díky čemuž lze stále v umocňování pokračovat), až se dostaneme k rovnici
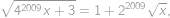
jejímž řešením je
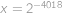 .
. Zkouškou ověříme, že toto číslo vyhovuje i původní rovnici.
Ülesanne 17
Nechť  ,
, 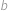 jsou takové konstanty, že body prostoru dané souřadnicemi
jsou takové konstanty, že body prostoru dané souřadnicemi 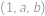 ,
, 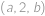 a
a 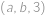 leží na jedné přímce. Určete
leží na jedné přímce. Určete 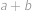 .
.
Peida / näita vastust
 .
.
Ülesanne 18
Najděte největší přirozené číslo  takové, aby číslo
takové, aby číslo 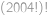 bylo dělitelné číslem
bylo dělitelné číslem 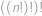 .
.
Peida / näita vastust
 .
.
Ülesanne 19
Funkce 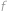 pro každé
pro každé 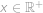 splňuje
splňuje 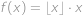 . Je-li
. Je-li 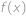 celé číslo, jaká je jeho největší možná dvojciferná hodnota? Výraz
celé číslo, jaká je jeho největší možná dvojciferná hodnota? Výraz 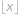 značí největší celé číslo, které nepřesahuje
značí největší celé číslo, které nepřesahuje  .
.
Peida / näita vastust
 .
.
Ülesanne 20
Jarda si upekl dokonale kulatou palačinku a z jejího středu vykrojil kruh, takže teď z palačinky zbylo mezikruží. Když se na ni chystal dát kečup, všiml si, že nejdelší rovná čára, kterou umí kečupem nakreslit, aniž by ho vylil na stůl, je dlouhá 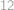 cm. Jaký obsah má Jardova palačinka?
cm. Jaký obsah má Jardova palačinka?
Peida / näita vastust
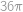 cm
cm .
.
Ülesanne 21
Spočtěte součet
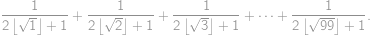
Peida / näita vastust
 .
.
Ülesanne 22
Vojenský pluk dlouhý tři kilometry pochoduje. Jejich nadřízený plukovník podél nich jezdí v autě třikrát rychleji, než vojáci pochodují. Vyjel s posledním vojákem a jede vždy přímo k prvnímu, otočí se a jede zpátky k poslednímu, pak se zase otočí a jede k prvnímu a tak pořád dokola. Jak daleko bude plukovník od posledního vojáka v momentě, kdy budou mít vojáci napochodováno 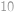 km?
km?
Peida / näita vastust
 km.
km.
Čas, za který vojáci ujdou 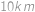 , si můžeme libovolně označit, tak si ho označne
, si můžeme libovolně označit, tak si ho označne 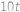 . Vojáci se potom pohybují rychlostí
. Vojáci se potom pohybují rychlostí  a plukovník jezdí rychlostí
a plukovník jezdí rychlostí  . Podívejme se, jak rychle se plukovník pohybuje vůči vojákům. Když jede stejným směrem, pohybuje se vůči nim
. Podívejme se, jak rychle se plukovník pohybuje vůči vojákům. Když jede stejným směrem, pohybuje se vůči nim  , takže od prvního vojáka přejede k poslednímu za
, takže od prvního vojáka přejede k poslednímu za 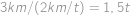 . Pokud jede opačně, má vůči vojákům rychlost
. Pokud jede opačně, má vůči vojákům rychlost  , takže od posledního k prvnímu přejede za
, takže od posledního k prvnímu přejede za 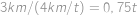 .
.
Tedy jedna „otočka“ od posledního znova k poslednímu mu trvá 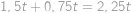 . To znamená, že plukovník za čas
. To znamená, že plukovník za čas 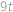 udělá čtyři otočky a bude zase u posledního vojáka. Do konce pochodování v tom momentě zůstane ještě
udělá čtyři otočky a bude zase u posledního vojáka. Do konce pochodování v tom momentě zůstane ještě  a plukovník se znovu bude pohybovat vůči vojákům
a plukovník se znovu bude pohybovat vůči vojákům  , takže už stihne přejet pouze
, takže už stihne přejet pouze 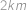 .
.
Ülesanne 23
Mějme trojúhelník 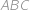 s úhly
s úhly 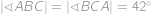 . Nechť
. Nechť 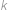 je kružnice se středem
je kružnice se středem 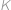 , která protíná stranu
, která protíná stranu 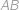 ve vnitřních bodech
ve vnitřních bodech 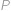 ,
,  , stranu
, stranu 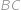 ve vnitřních bodech
ve vnitřních bodech 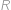 ,
, 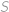 a stranu
a stranu 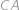 ve vnitřních bodech
ve vnitřních bodech 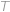 ,
, 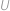 . Najděte úhel
. Najděte úhel 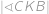 , jestliže víte, že
, jestliže víte, že 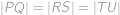 .
.
Peida / näita vastust
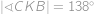 .
.
Ülesanne 24
Jaký zbytek dává 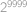 po dělení číslem
po dělení číslem 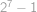 ?
?
Peida / näita vastust
 .
.
Zkusme postupně částečně dělit a vyjádřit 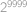 jako násobek
jako násobek 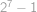 :
:
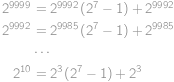
Na levé straně exponenty klesají po
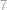
a protože
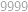
dává zbytek

po dělení
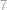 ,
, poslední člen na pravé straně musí být
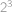 .
. Pokud nyní všechny rovnice sečteme, všechny mocniny

kromě
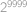
a
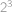
se budou vyskytovat na obou stranách rovnice, takže po jejich odečtení dostaneme:
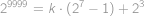
Z čehož hned plyne výsledek
 .
.
Ülesanne 25
Určete počet podmnožin množiny  takových, že součet jejich prvků je roven
takových, že součet jejich prvků je roven 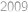 .
.
Peida / näita vastust
 .
.
Ülesanne 26
Najděte největší celé číslo, které dělí výraz  pro každé
pro každé 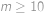 .
.
Peida / näita vastust
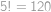 .
.
Daný mnohočlen rozložíme jako 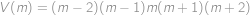 . Z tohoto rozkladu ihned vidíme, že
. Z tohoto rozkladu ihned vidíme, že  i
i  vždy dělí
vždy dělí 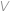 . Fakt, že
. Fakt, že  dělí
dělí 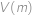 plyne ihned z toho, že dvě čísla z rozkladu
plyne ihned z toho, že dvě čísla z rozkladu 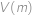 musí být sudá, navíc jsou po sobě jdoucí, tudíž je jedno z nich dělitelné
musí být sudá, navíc jsou po sobě jdoucí, tudíž je jedno z nich dělitelné  . Tedy víme, že
. Tedy víme, že 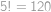 vždy dělí
vždy dělí 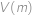 . Neexistenci většího dělitele dokážeme ve dvou krocích. Zaprvé volbou
. Neexistenci většího dělitele dokážeme ve dvou krocích. Zaprvé volbou 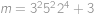 zaručíme, že žádná větší mocnina čísel
zaručíme, že žádná větší mocnina čísel  ,
,  a
a  nebude dělit
nebude dělit 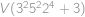 , protože „všechny vyšší mocniny budou schovány v
, protože „všechny vyšší mocniny budou schovány v 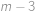 “. Zadruhé, volbou
“. Zadruhé, volbou 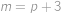 ,
, 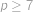 ,
, 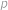 je prvočíslo, zaručíme, že
je prvočíslo, zaručíme, že 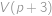 není dělitelné
není dělitelné 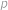 , neboť
, neboť 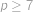 . Proto největší číslo, které dělí všechna
. Proto největší číslo, které dělí všechna 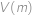 , je
, je 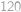 .
.
Ülesanne 27
Do kružnice je vepsaný šestiúhelník 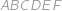 , pro který platí
, pro který platí 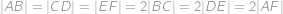 . Určete obvod
. Určete obvod 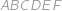 , víte-li, že
, víte-li, že 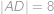 .
.
Peida / näita vastust
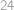 .
.
Ülesanne 28
Nechť 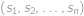 je libovolná permutace čísel
je libovolná permutace čísel 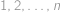 . Pro kolik z těchto permutací platí, že
. Pro kolik z těchto permutací platí, že 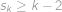 pro každé
pro každé 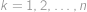 ?
?
Peida / näita vastust
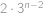 .
.
Ülesanne 29
Zjednodušte: 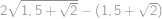 .
.
Peida / näita vastust
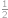 .
.
Ülesanne 30
Určete počet obdélníků (včetně čtverců) v tomto obrázku.
Peida / näita vastust
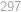 .
.
Spočítejme nejprve počet obdélníků, které by se v obrázku daly najít, kdyby uprostřed nebyla díra. Obdélník je jednoznačně dán dvojicí vodorovných a dvojicí svislých rovnoběžek. Vybíráme ze 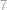 vodorovných (resp. svislých) čar, máme tedy
vodorovných (resp. svislých) čar, máme tedy 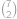 možností. Na vybrání obou dvojic pak zřejmě
možností. Na vybrání obou dvojic pak zřejmě 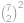 možností. Nyní budeme chtít odečíst ty obdélníky, které procházejí středem obrázku. Obdélníků, jejichž vodorovná přímka prochází středem a které nemají vrchol ve středu obrázku, je
možností. Nyní budeme chtít odečíst ty obdélníky, které procházejí středem obrázku. Obdélníků, jejichž vodorovná přímka prochází středem a které nemají vrchol ve středu obrázku, je 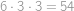 (
( možností za druhou vodorovnou hranu a
možností za druhou vodorovnou hranu a  možnosti pro boční hrany na obou stranách), stejně jako těch, jejichž svislá přímka prochází středem a které nemají vrchol ve středu obrázku. Obdélníků, jejichž jeden vrchol je střed obrázku, je celkem
možnosti pro boční hrany na obou stranách), stejně jako těch, jejichž svislá přímka prochází středem a které nemají vrchol ve středu obrázku. Obdélníků, jejichž jeden vrchol je střed obrázku, je celkem 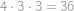 (
( za každý vrchol obdélníka a
za každý vrchol obdélníka a 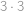 za zbylé dvě hrany). Celkový počet obdélníků tedy je
za zbylé dvě hrany). Celkový počet obdélníků tedy je 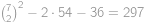 .
.
Ülesanne 31
Mřížový bod v rovině je takový, jehož obě souřadnice jsou celočíselné. Předpokládejme, že Pravoslav jde z bodu 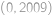 přímou cestou (po přímce) do náhodného mřížového bodu se souřadnicemi ve čtverci
přímou cestou (po přímce) do náhodného mřížového bodu se souřadnicemi ve čtverci 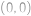 ,
, 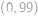 ,
, 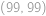 ,
, 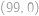 včetně hranic (každý cílový bod má stejnou pravděpodobnost). Jaká je pravděpodobnost, že jeho cesta bude procházet sudým počtem mřížových bodů? Do cesty počítáme i počátek a konec.
včetně hranic (každý cílový bod má stejnou pravděpodobnost). Jaká je pravděpodobnost, že jeho cesta bude procházet sudým počtem mřížových bodů? Do cesty počítáme i počátek a konec.
Peida / näita vastust
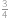 .
.
Nejdůležitější myšlenkou důkazu je uvědomit si, kolika mřížovými body procházíme, jdeme-li z bodu 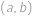 do bodu
do bodu 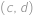 . Počet těchto bodů je roven
. Počet těchto bodů je roven 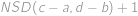 (a to včetně krajních bodů). V našem případě chceme zjistit, kdy počet protnutých mřížových bodů cesty z
(a to včetně krajních bodů). V našem případě chceme zjistit, kdy počet protnutých mřížových bodů cesty z 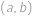 do
do 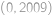 bude sudý pro
bude sudý pro 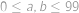 , stačí nám tedy zjistit, kdy je číslo
, stačí nám tedy zjistit, kdy je číslo 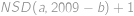 sudé, nebo ekvivalentně, kdy je
sudé, nebo ekvivalentně, kdy je 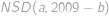 liché. Lichost
liché. Lichost 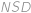 máme zaručenou, bude-li alespoň jedno z čísel
máme zaručenou, bude-li alespoň jedno z čísel  ,
, 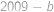 liché. Hodnota
liché. Hodnota  bude lichá v polovině případů
bude lichá v polovině případů 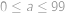 , hodnota
, hodnota 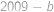 bude lichá taktéž v polovině případů. Proto
bude lichá taktéž v polovině případů. Proto 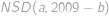 bude liché ve
bude liché ve 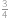 případů. Hledaná pravděpodobnost je tedy
případů. Hledaná pravděpodobnost je tedy 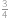 .
.
Ülesanne 32
Označme si 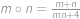 . Spočtěte
. Spočtěte
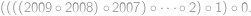
Peida / näita vastust
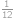 .
.
Ülesanne 33
Čtyřúhelník 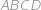 má délky stran
má délky stran 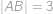 ,
, 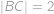 ,
, 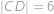 ,
, 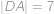 a platí
a platí 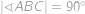 . Prozradíme vám, že tento čtyřúhelník má kružnici vepsanou. Dovedete určit její poloměr?
. Prozradíme vám, že tento čtyřúhelník má kružnici vepsanou. Dovedete určit její poloměr?
Peida / näita vastust
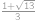 .
.
V řešení využijeme opakovaně Pythagrovu větu. Nejprve pomocí ní spočteme, že

Nyní si všimneme, že platí
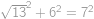 ,
, což říká, že i
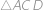
je pravoúhlý a platí
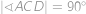 .
. K výpočtu poloměru

kružnice vepsané využijeme dvojí vyjádření obsahu
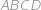 .
. 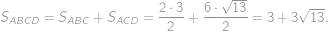
Označme nyní
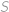
střed kružnice vepsané
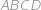
a pišme
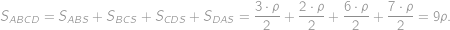
Srovnáním pak získáme
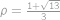 .
.
Ülesanne 34
Najděte všechna přirozená čísla  , pro která je výraz
, pro která je výraz 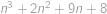 třetí mocninou nějakého přirozeného čísla.
třetí mocninou nějakého přirozeného čísla.
Peida / näita vastust
Peida / näita lahendust
Ülesanne 35
Mějme čtverec 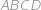 se stranou
se stranou 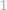 a uvnitř něj bod
a uvnitř něj bod 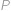 tak, že
tak, že 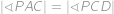 . Navíc víte, že
. Navíc víte, že 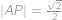 . Určete vzdálenost
. Určete vzdálenost 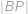 .
.
Peida / näita vastust
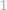 .
.
Ülesanne 36
Určete počet trojic přirozených čísel 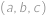 splňující následující vztahy
splňující následující vztahy
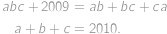
Peida / näita vastust
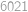 .
.
Hledejme nejprve řešení v nichž 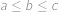 . Z obou rovnic vyjádříme
. Z obou rovnic vyjádříme 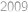 a srovnáním pravých stran dostaneme
a srovnáním pravých stran dostaneme
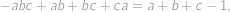
což upravíme na tvar
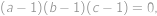
z něhož je zřejmé, že alespoň jedná neznámá musí být rovna
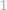 .
. V našem případě nutně
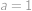 .
. Po dosazení do původních rovnic zjistíme, že stačí splnit podmínku
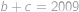 .
. Řešení, v nichž
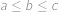 ,
, pak tvoří trojice
 .
. Vzhledem k symetrii zadané soustavy lze
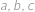
libovolně prohazovat, což v případě trojice, v níž jsou všechna čísla různá, dá

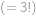
možností. Takové jsou všechny trojice kromě
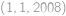 ,
, od níž můžeme přejít pouze ke trojicím
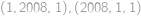 .
. Celkem tedy máme
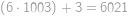
řešení.
Ülesanne 37
Mějme deset přirozených čísel uspořádaných do kruhu tak, že každé číslo je o jedna větší než největší společný dělitel jeho dvou sousedů. Najděte největší možný součet takto rozestavených čísel.
Peida / näita vastust
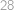 .
.
Ülesanne 38
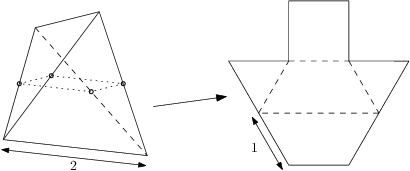
Je dán pravidelný čtyřstěn 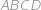 s délkou hrany
s délkou hrany  . Rovina
. Rovina  rovnoběžná s hranami
rovnoběžná s hranami 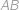 a
a  procházející středem
procházející středem 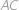 rozřízne
rozřízne 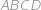 na dva kusy. Najděte povrch jednoho z těchto kusů.
na dva kusy. Najděte povrch jednoho z těchto kusů.
Peida / näita vastust
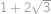 .
.
Ülesanne 39
Všechna políčka tabulky 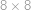 vyplníme křížky a kolečky tak, že v každém sloupci i v každém řádku bude lichý počet křížků. Kolika způsoby můžeme tabulku takto vyplnit?
vyplníme křížky a kolečky tak, že v každém sloupci i v každém řádku bude lichý počet křížků. Kolika způsoby můžeme tabulku takto vyplnit?
Peida / näita vastust
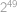 .
.
Ukážeme, že vyplnění tabulky je jednoznačně určené vyplněním jejího pravého dolního čtverce 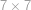 . Potom bude počet všech možností
. Potom bude počet všech možností 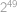 , protože pro každé z těchto políček máme dvě možnosti na vyplnění. Každé tabulce umíme zřejmě přiřadit vyplnění pravého dolního čtverce, takže stačí ukázat, že jeho vyplněním je už zbytek jednoznačně určený.
, protože pro každé z těchto políček máme dvě možnosti na vyplnění. Každé tabulce umíme zřejmě přiřadit vyplnění pravého dolního čtverce, takže stačí ukázat, že jeho vyplněním je už zbytek jednoznačně určený.
Máme-li vyplněný pravý dolní čtverec 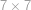 , symboly v prvním řádku a prvním sloupci kromě levého horního políčka jsou už jednoznačně určené tak, aby byla splněná podmínka parity pro řádky, resp. sloupce. Všimneme si, že kolečka v prvním sloupci (kromě levého horního políčka) jsou v těch řádcích, ve kterých pravý dolní čtverec obsahuje lichý počet křížků. Z toho vyplývá, že v pravém dolním čtverci je lichý počet křížků právě tehdy, když první sloupec (kromě levého horního políčka) obsahuje lichý počet křížků. Stejnou úvahu můžeme udělat i pro první řádek bez prvního políčka, takže parity symbolů v těchto oblastích jsou stejné a tedy symbol v levém horním políčku je tím jednoznačně určený.
, symboly v prvním řádku a prvním sloupci kromě levého horního políčka jsou už jednoznačně určené tak, aby byla splněná podmínka parity pro řádky, resp. sloupce. Všimneme si, že kolečka v prvním sloupci (kromě levého horního políčka) jsou v těch řádcích, ve kterých pravý dolní čtverec obsahuje lichý počet křížků. Z toho vyplývá, že v pravém dolním čtverci je lichý počet křížků právě tehdy, když první sloupec (kromě levého horního políčka) obsahuje lichý počet křížků. Stejnou úvahu můžeme udělat i pro první řádek bez prvního políčka, takže parity symbolů v těchto oblastích jsou stejné a tedy symbol v levém horním políčku je tím jednoznačně určený.
Ülesanne 40
V PraSátkově je 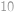 měst. Nově zakládaná společnost Čuňas\&*spol. chce vytvořit letecké linky mezi městy v PraSátkově. Ví však, že vláda hodlá rozdělit PraSátkov na dva státy, oba po pěti městech. Ale bohužel neví, která města budou ve kterém státě. Při rozdělení státu se všechny linky mezi městy z různých států zruší. Poraďte Čuňasům, jaký nejmenší počet linek jim stačí vytvořit, aby po rozdělení PraSátkova mohli cestující s použitím leteckých linek Čuňas\&*spol. cestovat mezi libovolnými městy v rámci rozdělených států (klidně i s přestupy).
měst. Nově zakládaná společnost Čuňas\&*spol. chce vytvořit letecké linky mezi městy v PraSátkově. Ví však, že vláda hodlá rozdělit PraSátkov na dva státy, oba po pěti městech. Ale bohužel neví, která města budou ve kterém státě. Při rozdělení státu se všechny linky mezi městy z různých států zruší. Poraďte Čuňasům, jaký nejmenší počet linek jim stačí vytvořit, aby po rozdělení PraSátkova mohli cestující s použitím leteckých linek Čuňas\&*spol. cestovat mezi libovolnými městy v rámci rozdělených států (klidně i s přestupy).
Peida / näita vastust
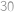 .
.
Podívejme se nejprve na jedno město, nazvěme ho Kocourkov. Kdyby z Kocourkova vedlo jenom pět linek, pak v rozdělení PraSátkova, při kterém by všech pět měst, kam Čuňasovi z Kocourkova létají, bylo spolu, nelétá žádná linka do Kocourkova (všechny byly zrušeny). Tudíž z každého města musí létat alespoň šest linek. Celkem tedy máme alespoň 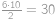 linek. Nyní ukážeme, že
linek. Nyní ukážeme, že 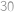 linek stačí. Uspořádejme si všech
linek stačí. Uspořádejme si všech 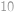 měst na kružnici a veďme linky vždy do
měst na kružnici a veďme linky vždy do  nejbližších měst (
nejbližších měst ( po levici,
po levici,  po pravici). Lze snadno nahlédnout, že nelze zvolit pět měst, které nebudou propojeny.
po pravici). Lze snadno nahlédnout, že nelze zvolit pět měst, které nebudou propojeny.
Ülesanne 41
Mějme tětivový čtyřúhelník 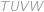 , jehož kružnice opsaná má poloměr
, jehož kružnice opsaná má poloměr  . Délky stran jsou
. Délky stran jsou 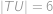 ,
,  ,
, 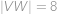 . Určete délku poslední strany.
. Určete délku poslední strany.
Peida / näita vastust
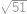 .
.
Ülesanne 42
Buď 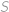 množina všech trojic přirozených čísel
množina všech trojic přirozených čísel 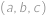 , pro něž platí
, pro něž platí 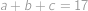 . Určete
. Určete
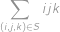
Peida / näita vastust
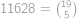 .
.
Ülesanne 43
Je dán trojúhelník 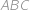 a jeho kružnice vepsaná se středem
a jeho kružnice vepsaná se středem 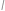 . Ta se dotýká strany
. Ta se dotýká strany 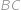 v bodě
v bodě  . Označme
. Označme 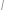 kružnici nad průměrem
kružnici nad průměrem 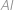 . Buď
. Buď  její druhý průsečík s přímkou
její druhý průsečík s přímkou 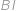 a
a 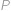 její druhý průsečík s přímkou
její druhý průsečík s přímkou 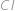 . Víte-li, že
. Víte-li, že 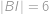 ,
, 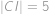 ,
, 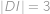 , určete
, určete 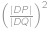 .
.
Peida / näita vastust
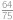 .
.
Předně si označme 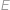 ,
, 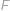 body dotyku kružnice vepsané postupně se stranami
body dotyku kružnice vepsané postupně se stranami 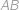 ,
, 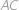 a uvědomme si, že tyto body leží na kružnici
a uvědomme si, že tyto body leží na kružnici 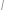 . Nyní porovnáme velikosti úhlů
. Nyní porovnáme velikosti úhlů 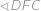 a
a 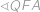 .
.
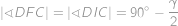
Přičemž v první rovnosti jsme využili, že i čtyřúhelník
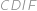
je tětivový a v druhé dopočet úhlů v
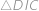
. Dále
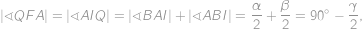
kde jsme v první rovnosti pro změnu využili, že
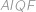
je tětivový a v druhé jsme dopočítali úhly v
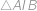
. Víme tedy, že
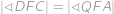 ,
, což znamená, že body
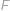 ,
, 
a

leží v přímce. Obdobně odvodíme, že i body
 ,
, 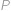
a
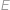
leží v přímce. Vezměme nyní mocnost bodu D k (tětivovému) čtyřúhelníku
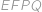 .
. Získáme

Stačí tedy vypočítat délky úseček
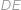
a
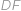 ,
, což již není těžké. Kupříkladu
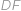
je dvojnásobkem výšky v pravoúhlém trojúhelníku
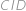 ,
, jehož strany dovedeme určit, a tuto výšku tak umíme dopočíst třeba užitím jedné z Euklidových vět. Nakonec vypočteme
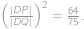
Ülesanne 44
Je dána tabulka  x
x , v jejímž levém horním rohu je číslo
, v jejímž levém horním rohu je číslo 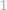 a v pravém dolním je číslo
a v pravém dolním je číslo 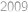 . Rozhodněte, kolika způsoby lze vyplnit zbylá políčka tak, aby každé číslo dělilo číslo v políčku pod ním i číslo vpravo od něj.
. Rozhodněte, kolika způsoby lze vyplnit zbylá políčka tak, aby každé číslo dělilo číslo v políčku pod ním i číslo vpravo od něj.
Peida / näita vastust
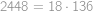 .
.
Nejprve rozložíme 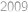 jako
jako 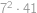 a rozmyslíme si, že dělitelnost čísly
a rozmyslíme si, že dělitelnost čísly 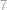 a
a 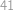 je možné řešit zvlášť. Uvažujme nejprve dělitelnost číslem
je možné řešit zvlášť. Uvažujme nejprve dělitelnost číslem 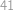 . Označme
. Označme 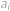 počet výskytů čísla
počet výskytů čísla 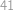 v
v 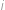 -tém sloupci. Požadavek ze zadání zaručí
-tém sloupci. Požadavek ze zadání zaručí 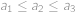 a
a 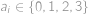 pro
pro 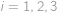 . A i naopak, každá taková posloupnost (s výjimkou
. A i naopak, každá taková posloupnost (s výjimkou 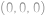 a
a 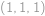 ) jednoznačně určuje vyhovující rozmístění čísel
) jednoznačně určuje vyhovující rozmístění čísel 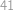 . Ať už rozborem případů či jinak dojdeme k tomu, že takových posloupností je
. Ať už rozborem případů či jinak dojdeme k tomu, že takových posloupností je 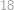 . Zabývejme se nyní zvlášť dělitelností sedmi a podle hodnoty prostředního políčka, rozlišme tři případy.
. Zabývejme se nyní zvlášť dělitelností sedmi a podle hodnoty prostředního políčka, rozlišme tři případy.
- Uprostřed je
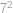 .
. Vpravo a dolů od prostředka budou též násobky 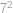 . Zbývá určit, kolika způsoby lze vyplnit zbylá políčka. Zkoumejme dvě nevyplněná políčka v horním řádku. Rozborem možností zjistíme, že mohou být vyplněna
. Zbývá určit, kolika způsoby lze vyplnit zbylá políčka. Zkoumejme dvě nevyplněná políčka v horním řádku. Rozborem možností zjistíme, že mohou být vyplněna  způsoby. Obdobně políčka v prvním sloupci mohou být vyplněna
způsoby. Obdobně políčka v prvním sloupci mohou být vyplněna  způsoby. Navíc jsou tato vyplnění nezávislá, takže celkem máme
způsoby. Navíc jsou tato vyplnění nezávislá, takže celkem máme 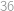 možností.
možností.
- Uprostřed je
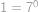 .
. Stejnou úvahou jako v předchozím případě určíme, že možností je 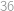 .
.
- Uprostřed je
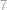 .
. Políčka, která zbývá vyplnit rozdělíme na dvě trojice, jejichž vyplnění bude opět nezávislé. Trojici budou tvořit políčka, která jsou vpravo nahoře (resp. vlevo dole) od prostředka. Na vyplnění jedné z těchto trojic je  možností. Takže celkem je možností
možností. Takže celkem je možností 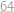 .
.
Máme tedy 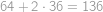 možností, jak vyplnit do tabulky mocniny čísla
možností, jak vyplnit do tabulky mocniny čísla 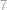 a
a 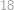 možností, jak vyplnit mocniny čísla
možností, jak vyplnit mocniny čísla 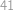 . Znovu si rozmyslíme, že tato vyplnění jsou nezávislá a zkonstatujeme, že celkový možný počet vyplnění je
. Znovu si rozmyslíme, že tato vyplnění jsou nezávislá a zkonstatujeme, že celkový možný počet vyplnění je 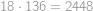 možností.
možností.
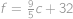 (
( jsou stupně Celsiovy,
jsou stupně Celsiovy, 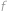 Farenheitovy). Jakou teplotu vyjádří Evropan i Američan stejnou hodnotou?
Farenheitovy). Jakou teplotu vyjádří Evropan i Američan stejnou hodnotou?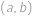 takové, že čísla
takové, že čísla 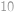 ,
, ,
, 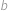 ,
,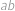 tvoří v tomto pořadí aritmetickou posloupnost.
tvoří v tomto pořadí aritmetickou posloupnost.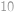 otázek, na které lze odpovídat pouze ANO nebo NE. Test je připraven natolik fikaně, že odpoví-li Miloš na libovolných pět otázek ANO a na zbylých pět otázek NE, bude mít vždy alespoň čtyři správné odpovědi. Zjistěte, kolika způsoby lze takovýto test připravit.
otázek, na které lze odpovídat pouze ANO nebo NE. Test je připraven natolik fikaně, že odpoví-li Miloš na libovolných pět otázek ANO a na zbylých pět otázek NE, bude mít vždy alespoň čtyři správné odpovědi. Zjistěte, kolika způsoby lze takovýto test připravit. tak, aby nerovnice
tak, aby nerovnice 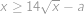 platila pro všechna nezáporná čísla
platila pro všechna nezáporná čísla  .
.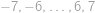 tak, aby absolutní hodnota čísel v seřazené posloupnosti byla neklesající?
tak, aby absolutní hodnota čísel v seřazené posloupnosti byla neklesající? tvořený čtyřbokými jehlany
tvořený čtyřbokými jehlany 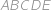 a
a 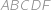 .
. .
.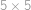 jsou po řádcích (a v rámci řádku zleva doprava) vepsána čísla
jsou po řádcích (a v rámci řádku zleva doprava) vepsána čísla 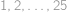 v tomto pořadí. Vybereme pět políček tak, aby žádná dvě nebyla ve stejném řádku ani ve stejném sloupci, a čísla na těchto políčkách sečteme. Jaké hodnoty součtu můžeme tímto způsobem dostat?
v tomto pořadí. Vybereme pět políček tak, aby žádná dvě nebyla ve stejném řádku ani ve stejném sloupci, a čísla na těchto políčkách sečteme. Jaké hodnoty součtu můžeme tímto způsobem dostat?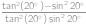 .
.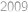 po sobě jdoucích přirozených čísel, která měla stejný součet jako
po sobě jdoucích přirozených čísel, která měla stejný součet jako 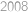 po nich následujících čísel. Které z Kátiných čísel bylo nejmenší?
po nich následujících čísel. Které z Kátiných čísel bylo nejmenší?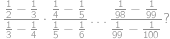
 reálné číslo a
reálné číslo a 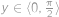 splňující rovnice
splňující rovnice 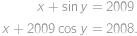
 .
.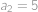 a
a 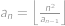 pro
pro 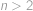 .
.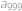 .
.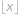 značí největší celé číslo, které nepřesahuje
značí největší celé číslo, které nepřesahuje  .
. není
není  násobkem
násobkem 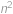 ?
?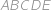 .
.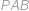 tak, aby bod
tak, aby bod 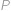 ležel uvnitř pětiúhelníka. Kolik stupňů má úhel
ležel uvnitř pětiúhelníka. Kolik stupňů má úhel 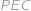 ?
?
 ,
,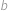 jsou takové konstanty, že body prostoru dané souřadnicemi
jsou takové konstanty, že body prostoru dané souřadnicemi 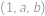 ,
,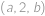 a
a 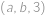 leží na jedné přímce. Určete
leží na jedné přímce. Určete 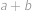 .
. takové, aby číslo
takové, aby číslo 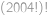 bylo dělitelné číslem
bylo dělitelné číslem 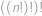 .
.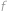 pro každé
pro každé 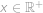 splňuje
splňuje 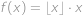 .
.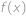 celé číslo, jaká je jeho největší možná dvojciferná hodnota? Výraz
celé číslo, jaká je jeho největší možná dvojciferná hodnota? Výraz 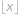 značí největší celé číslo, které nepřesahuje
značí největší celé číslo, které nepřesahuje  .
.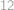 cm. Jaký obsah má Jardova palačinka?
cm. Jaký obsah má Jardova palačinka?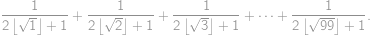
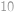 km?
km?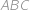 s úhly
s úhly 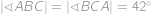 .
.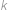 je kružnice se středem
je kružnice se středem 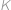 ,
,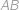 ve vnitřních bodech
ve vnitřních bodech 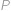 ,
, , stranu
, stranu 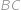 ve vnitřních bodech
ve vnitřních bodech 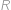 ,
,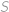 a stranu
a stranu 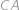 ve vnitřních bodech
ve vnitřních bodech 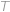 ,
,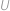 . Najděte úhel
. Najděte úhel 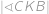 ,
,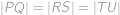 .
.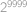 po dělení číslem
po dělení číslem 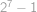 ?
? takových, že součet jejich prvků je roven
takových, že součet jejich prvků je roven 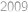 .
. pro každé
pro každé 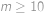 .
.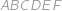 ,
,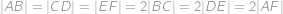 .
.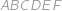 ,
,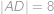 .
.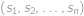 je libovolná permutace čísel
je libovolná permutace čísel 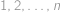 .
.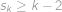 pro každé
pro každé 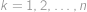 ?
?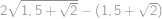 .
.
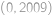 přímou cestou (po přímce) do náhodného mřížového bodu se souřadnicemi ve čtverci
přímou cestou (po přímce) do náhodného mřížového bodu se souřadnicemi ve čtverci 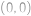 ,
,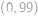 ,
, 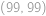 ,
,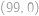 včetně hranic (každý cílový bod má stejnou pravděpodobnost). Jaká je pravděpodobnost, že jeho cesta bude procházet sudým počtem mřížových bodů? Do cesty počítáme i počátek a konec.
včetně hranic (každý cílový bod má stejnou pravděpodobnost). Jaká je pravděpodobnost, že jeho cesta bude procházet sudým počtem mřížových bodů? Do cesty počítáme i počátek a konec.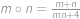 .
.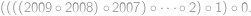
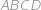 má délky stran
má délky stran 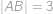 ,
,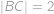 ,
, 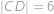 ,
,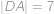 a platí
a platí 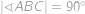 .
. ,
,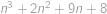 třetí mocninou nějakého přirozeného čísla.
třetí mocninou nějakého přirozeného čísla.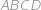 se stranou
se stranou 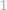 a uvnitř něj bod
a uvnitř něj bod 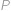 tak, že
tak, že 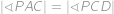 .
.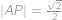 .
.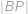 .
.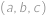 splňující následující vztahy
splňující následující vztahy 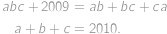
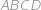 s délkou hrany
s délkou hrany  .
. rovnoběžná s hranami
rovnoběžná s hranami 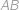 a
a  procházející středem
procházející středem 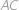 rozřízne
rozřízne 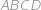 na dva kusy. Najděte povrch jednoho z těchto kusů.
na dva kusy. Najděte povrch jednoho z těchto kusů.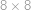 vyplníme křížky a kolečky tak, že v každém sloupci i v každém řádku bude lichý počet křížků. Kolika způsoby můžeme tabulku takto vyplnit?
vyplníme křížky a kolečky tak, že v každém sloupci i v každém řádku bude lichý počet křížků. Kolika způsoby můžeme tabulku takto vyplnit?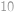 měst. Nově zakládaná společnost Čuňas\&*spol. chce vytvořit letecké linky mezi městy v PraSátkově. Ví však, že vláda hodlá rozdělit PraSátkov na dva státy, oba po pěti městech. Ale bohužel neví, která města budou ve kterém státě. Při rozdělení státu se všechny linky mezi městy z různých států zruší. Poraďte Čuňasům, jaký nejmenší počet linek jim stačí vytvořit, aby po rozdělení PraSátkova mohli cestující s použitím leteckých linek Čuňas\&*spol. cestovat mezi libovolnými městy v rámci rozdělených států (klidně i s přestupy).
měst. Nově zakládaná společnost Čuňas\&*spol. chce vytvořit letecké linky mezi městy v PraSátkově. Ví však, že vláda hodlá rozdělit PraSátkov na dva státy, oba po pěti městech. Ale bohužel neví, která města budou ve kterém státě. Při rozdělení státu se všechny linky mezi městy z různých států zruší. Poraďte Čuňasům, jaký nejmenší počet linek jim stačí vytvořit, aby po rozdělení PraSátkova mohli cestující s použitím leteckých linek Čuňas\&*spol. cestovat mezi libovolnými městy v rámci rozdělených států (klidně i s přestupy).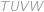 ,
, .
.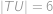 ,
, ,
, 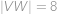 .
.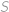 množina všech trojic přirozených čísel
množina všech trojic přirozených čísel 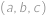 ,
,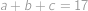 .
.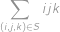
 a jeho kružnice vepsaná se středem
a jeho kružnice vepsaná se středem  .
. v bodě
v bodě  .
. kružnici nad průměrem
kružnici nad průměrem 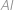 .
. její druhý průsečík s přímkou
její druhý průsečík s přímkou 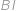 a
a 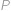 její druhý průsečík s přímkou
její druhý průsečík s přímkou 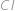 .
.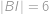 ,
,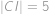 ,
, 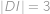 ,
,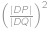 .
. x
x ,
,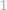 a v pravém dolním je číslo
a v pravém dolním je číslo 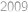 .
.
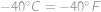 .
.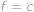 .
.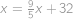 .
.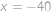 .
.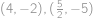 .
.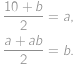
 .
.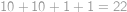 .
. .
.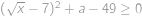 .
.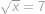 ,
,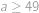 .
.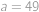 stačí a toto
stačí a toto 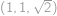 ,
,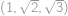 a
a 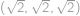 .
.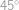 a
a 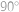 ,
,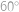 .
.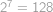 .
.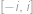 máme tedy
máme tedy 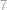 a jejich řazení je nezávislé. Celkem tedy
a jejich řazení je nezávislé. Celkem tedy 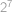 možností.
možností. .
.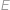 ,
,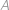 a
a 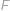 .
.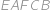 je jehlan s podstavou
je jehlan s podstavou 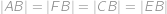 ,
,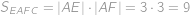
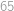 .
.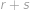 ,
,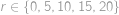 a
a 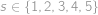 .
. a číslům ve stejném sloupci patří stejné číslo
a číslům ve stejném sloupci patří stejné číslo  .
.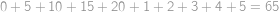 .
.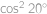 a pak upravíme
a pak upravíme 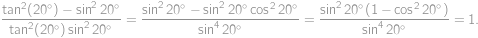
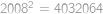 .
.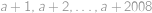 přičteme 2008 a sečteme je, dostaneme součet těch 2008 následujících čísel. Zadání ale říká, že zároveň dostaneme stejný výsledek, jako když k součtu čísel
přičteme 2008 a sečteme je, dostaneme součet těch 2008 následujících čísel. Zadání ale říká, že zároveň dostaneme stejný výsledek, jako když k součtu čísel 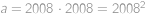 .
.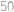 .
.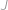 .
.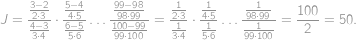
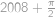 .
.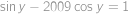 .
.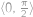 nezáporný a sinus tam má maximum 1, tak aby výraz na levé straně mohl být 1, musí být
nezáporný a sinus tam má maximum 1, tak aby výraz na levé straně mohl být 1, musí být 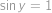 a
a 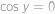 , neboli
, neboli 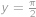 .
.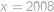 a v součtu
a v součtu 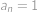 pro
pro 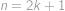 a
a 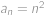 pro
pro 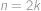 ,
,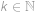 .
.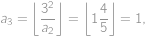
 ,
, ,
, 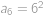 ,… ,
,… ,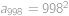 a
a 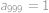 .
. .
.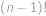 násobkem
násobkem 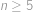 složené číslo, rozlišíme dva případy.
složené číslo, rozlišíme dva případy. 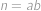 pro nějaká
pro nějaká  .
.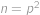 , pro nějaké prvočíslo
, pro nějaké prvočíslo 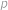 .
.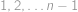 čísla
čísla 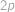 (díky nerovnosti
(díky nerovnosti 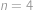 .
.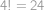 není násobkem
není násobkem 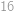 .
.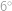 .
.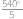 ).
).
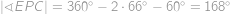 a z rovnoramennosti trojúhelníku
a z rovnoramennosti trojúhelníku 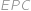 už lehko dopočteme
už lehko dopočteme 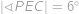 .
.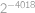 .
.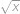 a začneme postupně umocňovat (vždy se některé členy odečtou, díky čemuž lze stále v umocňování pokračovat), až se dostaneme k rovnici
a začneme postupně umocňovat (vždy se některé členy odečtou, díky čemuž lze stále v umocňování pokračovat), až se dostaneme k rovnici 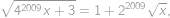
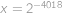 .
.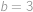 .
.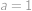 .
.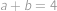 .
. .
.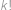 dělí číslo
dělí číslo  pro libovolná
pro libovolná  ,
,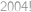 větší nebo rovno
větší nebo rovno 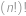 ,
,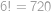 a
a 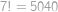 ,
,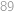 .
.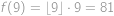 a
a 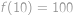 .
.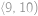 .
.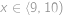 platí
platí 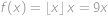 .
.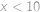 dále platí
dále platí 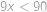 ,
,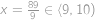 .
.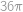 cm
cm .
.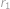 poloměr původní palačinky a
poloměr původní palačinky a 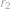 poloměr vyříznutého kruhu, tak z Pythagorovy věty
poloměr vyříznutého kruhu, tak z Pythagorovy věty 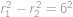 .
.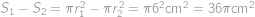 .
.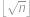 .
.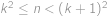 je
je 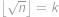 ,
,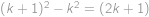 -krát.
-krát.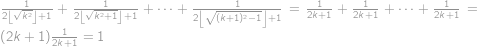 .
.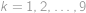 ,
,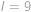 .
.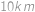 ,
,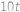 .
. a plukovník jezdí rychlostí
a plukovník jezdí rychlostí  .
. ,
,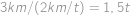 .
. ,
,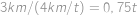 .
.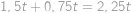 .
.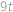 udělá čtyři otočky a bude zase u posledního vojáka. Do konce pochodování v tom momentě zůstane ještě
udělá čtyři otočky a bude zase u posledního vojáka. Do konce pochodování v tom momentě zůstane ještě  a plukovník se znovu bude pohybovat vůči vojákům
a plukovník se znovu bude pohybovat vůči vojákům 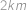 .
.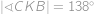 .
.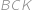 dva úhly rovny
dva úhly rovny 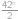 a snadno se dopočte, že hodnota třetího úhlu
a snadno se dopočte, že hodnota třetího úhlu 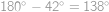 .
. .
.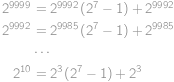
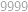 dává zbytek
dává zbytek 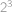 .
.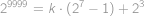
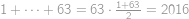 ,
,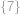 ,
,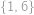 ,
, 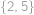 ,
,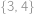 a
a 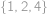 ,
,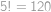 .
.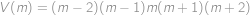 .
.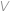 .
.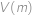 plyne ihned z toho, že dvě čísla z rozkladu
plyne ihned z toho, že dvě čísla z rozkladu 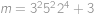 zaručíme, že žádná větší mocnina čísel
zaručíme, že žádná větší mocnina čísel 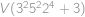 ,
,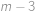 “. Zadruhé, volbou
“. Zadruhé, volbou 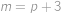 ,
,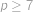 ,
, 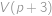 není dělitelné
není dělitelné 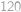 .
.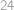 .
.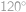 ,
,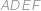 ,
,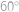 ,
,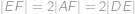 lze lichoběžník
lze lichoběžník 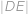 ,
,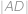 .
.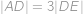 a
a 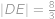 .
.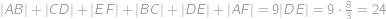 .
.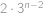 .
.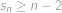 ,
,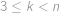 mohu (díky podmínce
mohu (díky podmínce 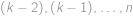 .
.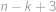 možností. Všechna čísla větší než
možností. Všechna čísla větší než 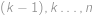 ,
,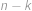 míst. A proto mi zbyla
míst. A proto mi zbyla 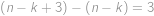 volná místa pro položení čísla
volná místa pro položení čísla 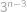 možností. Pro
možností. Pro 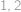 .
.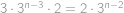 možností.
možností.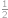 .
.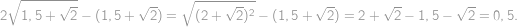
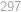 .
.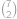 možností. Na vybrání obou dvojic pak zřejmě
možností. Na vybrání obou dvojic pak zřejmě 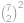 možností. Nyní budeme chtít odečíst ty obdélníky, které procházejí středem obrázku. Obdélníků, jejichž vodorovná přímka prochází středem a které nemají vrchol ve středu obrázku, je
možností. Nyní budeme chtít odečíst ty obdélníky, které procházejí středem obrázku. Obdélníků, jejichž vodorovná přímka prochází středem a které nemají vrchol ve středu obrázku, je 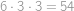 (
(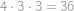 (
(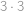 za zbylé dvě hrany). Celkový počet obdélníků tedy je
za zbylé dvě hrany). Celkový počet obdélníků tedy je 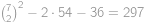 .
.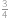 .
.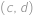 .
.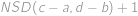 (a to včetně krajních bodů). V našem případě chceme zjistit, kdy počet protnutých mřížových bodů cesty z
(a to včetně krajních bodů). V našem případě chceme zjistit, kdy počet protnutých mřížových bodů cesty z 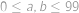 ,
,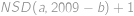 sudé, nebo ekvivalentně, kdy je
sudé, nebo ekvivalentně, kdy je 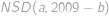 liché. Lichost
liché. Lichost 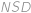 máme zaručenou, bude-li alespoň jedno z čísel
máme zaručenou, bude-li alespoň jedno z čísel 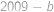 liché. Hodnota
liché. Hodnota 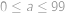 ,
,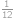 .
.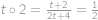 .
.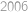 operacích a dostaneme výsledek
operacích a dostaneme výsledek 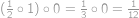 .
.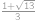 .
.
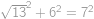 ,
,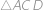 je pravoúhlý a platí
je pravoúhlý a platí 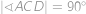 .
.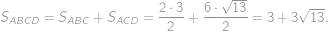
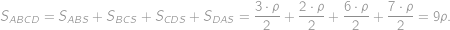
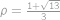 .
.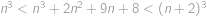 musí nastat rovnost
musí nastat rovnost 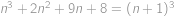 .
.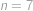 .
.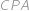 (shodnost obvodového a úsekového úhlu). Střed
(shodnost obvodového a úsekového úhlu). Střed 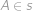 ,
, středem
středem 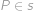 ,
,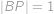 .
.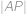 ,
,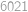 .
.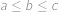 .
.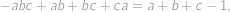
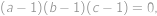
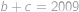 .
. .
.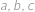 libovolně prohazovat, což v případě trojice, v níž jsou všechna čísla různá, dá
libovolně prohazovat, což v případě trojice, v níž jsou všechna čísla různá, dá 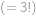 možností. Takové jsou všechny trojice kromě
možností. Takové jsou všechny trojice kromě 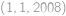 ,
,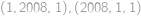 .
.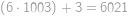 řešení.
řešení.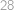 .
. .
.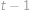 ,
,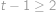 ,
, druhého souseda jednoho z čísel
druhého souseda jednoho z čísel 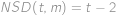 ,
,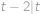 a máme
a máme 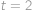 a
a 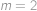 .
. ,
, .
. ,
,
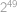 .
.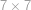 .
.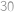 .
.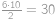 linek. Nyní ukážeme, že
linek. Nyní ukážeme, že 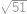 .
.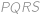 s délkami stran
s délkami stran 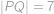 ,
,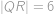 a
a 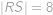 (první dvě délky stran jsou zaměněny) a poloměrem kružnice opsané
(první dvě délky stran jsou zaměněny) a poloměrem kružnice opsané 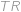 na
na 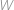 jen přeznačili na
jen přeznačili na 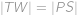 nezměnila. Ve čtyřúhelníku
nezměnila. Ve čtyřúhelníku 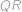 a
a 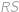 tvoří pravoúhlý trojúhelník o stranách délek
tvoří pravoúhlý trojúhelník o stranách délek 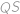 je průměr
je průměr 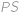 :
: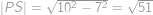 .
.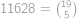 .
.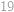 různých kuliček a snažme se z nich vybrat
různých kuliček a snažme se z nich vybrat 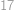 rozdělí do tří neprázdných (rozmysli si!) úseků. Počty kuliček v těchto úsecích označme (zleva)
rozdělí do tří neprázdných (rozmysli si!) úseků. Počty kuliček v těchto úsecích označme (zleva) 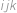 možností. Zbývá si uvědomit, že různými volbami první dvojice kuliček získáváme různá řešení rovnice
možností. Zbývá si uvědomit, že různými volbami první dvojice kuliček získáváme různá řešení rovnice 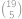 .
.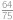 .
.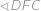 a
a 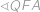 .
.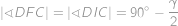
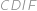 je tětivový a v druhé dopočet úhlů v
je tětivový a v druhé dopočet úhlů v 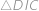 . Dále
. Dále 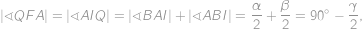
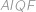 je tětivový a v druhé jsme dopočítali úhly v
je tětivový a v druhé jsme dopočítali úhly v 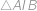 . Víme tedy, že
. Víme tedy, že 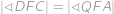 ,
,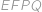 .
.
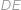 a
a 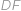 ,
,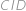 ,
,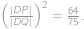
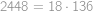 .
.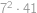 a rozmyslíme si, že dělitelnost čísly
a rozmyslíme si, že dělitelnost čísly 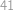 je možné řešit zvlášť. Uvažujme nejprve dělitelnost číslem
je možné řešit zvlášť. Uvažujme nejprve dělitelnost číslem 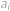 počet výskytů čísla
počet výskytů čísla 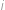 -tém sloupci. Požadavek ze zadání zaručí
-tém sloupci. Požadavek ze zadání zaručí 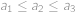 a
a 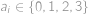 pro
pro 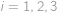 .
.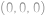 a
a 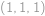 )
)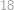 .
.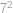 .
.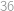 možností.
možností. 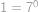 .
.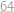 .
.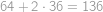 možností, jak vyplnit do tabulky mocniny čísla
možností, jak vyplnit do tabulky mocniny čísla 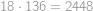 možností.
možností.



















