1 J
Given that there is exactly one way to write 2013 as a sum of two primes find the product of these primes.
4022
2 J
Two circles with radius 1 intersect each other. The area of their intersection equals the sum of the areas of the two outer parts. What is the area of the intersection?
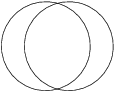
\frac23\pi
3 J
We have several pins five of which are yellow, four red, three green, two blue, and the remaining one is orange. In how many ways can we place them in the given triangular grid (see diagram) so that no pair of pins with the same color is in the same row or column? The pins of the same color are considered indistinguishable.

1
4 J
Find the smallest positive integer whose product of digits equals 600.
3558
5 J
Positive real numbers a and b satisfy What is the value of ab+\frac{1}{ab}?
33
6 J
Luke has a six-digit number which satisfies the following conditions:
- The number reads the same from left to right as from right to left.
- It is divisible by 9.
- After crossing out its first and last digit the only prime factor of the resulting number is 11.
What is Luke’s number?
513315
7 J
Point D lies on the diameter AB of the semicircle k. A perpendicular to AB through point D intersects k at point C. The lengths of the arcs AC and CB of k are in the ratio 1:2. Find AD : DB.
1 : 3
8 J
Two spoilt brothers Jim and Tim got a bag of chocolate chips and split them evenly. Both of them eat from two to three chocolate chips a day. Jim finished his chips after fourteen days, Tim after exactly three weeks. How many chocolate chips were there in the bag?
84
9 J
In how many ways can we read the word Náboj in the diagram?
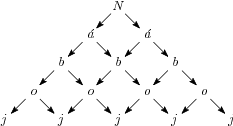
16
10 J
Inhabitants of an island are either liars or truth-tellers. Twelve of them sit around a table. They all claim to be truth-tellers and also claim that the person to their right is a liar. What is the maximum possible number of liars in such a group?
6
11 J / 1 S
Jane has 11 congruent square tiles six of which are red, three blue, and two green. In how many ways can she construct a 3 \times 3 square from 9 of the 11 tiles such that the coloring of the square remains intact if we rotate the square by 90^\circ clockwise around its center? Two tiles of the same color are considered indistinguishable.
0
12 J / 2 S
Two fifths of males and three fifths of females living on a certain island are married. What percentage of the island’s inhabitants is married?
48 \%=\frac{12}{25}
13 J / 3 S
What is the maximum side length of an equilateral triangle which can be cut from a rectangular-shaped paper with dimensions 21 \times 29.7\,\text{cm}?
14\sqrt3 = \frac{42}{\sqrt{3}}\,\text{cm}
14 J / 4 S
Kate took a square piece of paper and repeatedly folded it in half until it was done four times. After every fold, she was left with an isosceles right triangle. How many squares can one see after unfolding the paper?
10
15 J / 5 S
How many pentagons are there in the figure?
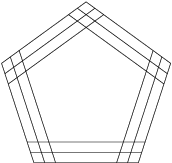
3^5=243
16 J / 6 S
Joseph wanted to add two positive integers but accidentally wrote a zero digit to the end of one of them. The result he obtained was 3858 instead of the correct 2013. Find the value of the larger summand.
1808
17 J / 7 S
What is the radius of the smallest circle which can cover a triangle with side lengths 3, 5, and 7?
3.5
18 J / 8 S
Lisa, Mary, Nancy and Susan have 100 lollipops altogether. Each pair of them has at least 41 lollipops. What is the minimum number of lollipops that Lisa can have?
12
19 J / 9 S
The area of a rectangle ABCD is 80 and the length of its diagonal is 16. Find the sine of the angle between its diagonals.
\frac58 = 0.625
20 J / 10 S
What is the largest possible value of a^b + c^d, where a, b, c, and d are distinct elements of the set \{-7, -5, -4, -3, -2, -1\}?
(-1)^{-4}+(-3)^{-2}=\frac{10}{9}
21 J / 11 S
An angle of magnitude 110^\circ is placed in the coordinate plane at random. What is the probability that its legs form a graph of some function?
\frac{11}{18}
22 J / 12 S
James drew a regular 100-gon A_1A_2 \dots A_{100} (numbered clockwise) on the last year’s Náboj (23rd March, 2012) and randomly placed a chip on one of the vertices. Every following day, he moved the chip clockwise by the number of vertices indicated by the number of the current vertex (from A_3 he would move it to A_6, from A_{96} to A_{92}). Now the chip lies on A_{100}. What was the probability this would happen?
0.04=\frac1{25}
23 J / 13 S
A positive integer is called differential if it can be written as a difference of squares of two integers. How many of the numbers 1,2, \dots, 2013 are differential?
1510
24 J / 14 S
Three non-overlapping regular convex polygons with side length 1 have point A in common and their union forms a (nonconvex) polygon M which has A in its interior. If one of the regular polygons is a square and another is a hexagon, find the perimeter of M.
16
25 J / 15 S
Mike wrote the numbers from 1 to 100 in random order. What is the probability that for each i = 1,\dots,50 the number on the position 2i-1 is smaller than the number on the position 2i?
2^{-50}
26 J / 16 S
Pink paint is made up of red and white paint in the ratio 1:1, cyan paint is made up of blue and white in the ratio 1:2. Karen intends to paint her room with paint which is made up of pink and cyan in the ratio 2:1. She has already mixed three tins of blue and one tin of red paint. How many tins does she have to add to the mixture, provided there are only red and white tins left?
23
27 J / 17 S
We have a hat with several white, gray, and black rabbits. When a magician starts taking them randomly out of the hat (without returning them), the probability of him taking a white rabbit before a gray one is \frac34. The probability of him taking a gray rabbit before a black one is \frac34 as well. What is the probability of him taking a white rabbit before a black one?
\frac{9}{10}
28 J / 18 S
Positive integers a, b satisfy 49a+99b = 2013. Find the value of a+b.
37
29 J / 19 S
In the corners of a square PQRS with side length 6\,\text{cm} four smaller squares are placed with side lengths 2\,\text{cm}. Let us denote their vertices W, X, Y, Z like in the picture. A square ABCD is constructed in such a way, that points W, X, Y, Z lie inside the sides AB, BC, CD, DA respectively. Find the largest possible distance between points P and D.
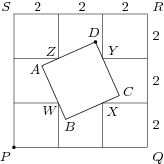
6
30 J / 20 S
We have twenty boxes of apples that altogether contain 129 apples. We know that in some of the boxes there are exactly 4 apples and all the remaining boxes contain exactly x apples. Find all possible values of x.
11, 53
31 J / 21 S
Consider real numbers a, b such that a > b > 0 and Find the value of the expression \frac{a+b}{a-b}.
\sqrt{\frac{2015}{2011}}
32 J / 22 S
In how many ways can we fill in individual squares in the pictured heptomino piece with numbers 1 to 7 (each of which should be used once only) so that the sum of numbers in the bottom row is the same as the sum of numbers in the left column?
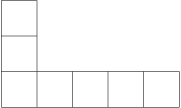
144=3 \cdot 2 \cdot 4!
33 J / 23 S
Let ABC be an acute triangle with AB=4\pi, BC=4\pi+3, CA=4\pi+6. Denote by D the foot of the A-altitude. Find CD-BD.
12
34 J / 24 S
Trams have the same intervals all day and in both directions. A pedestrian walked along the tram rails and observed that every 12 minutes he was overtaken by a tram, and every 4 minutes one tram coming in the opposite direction passed him. What is the time interval between two trams?
6 minutes
35 J / 25 S
How many nondegenerate triangles can be formed by means of joining some point triplet from the picture?
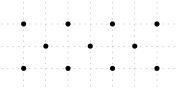
Note: Points are aligned in the indicated grid.
148=\binom{11}{3}-17
36 J / 26 S
Thomas got a box of chocolates with 30 sweets arranged in three rows by ten. He is eating the sweets one by one in such a way that the number of sweets in two rows always differs at most by one. In how many ways can he eat the whole box?
6^{10}\cdot (10!)^3
37 J / 27 S
We call a positive integer with six digits doubling if the first three digits are the same (including the order) as the other three digits. For example the number 227227 is doubling, but 135153 is not doubling. How many six-digit doubling numbers are divisible by 2013?
Note: The first digit of a positive integer cannot be 0.
5
38 J / 28 S
Suppose that we have 4\times 4 chessboard and on each square we draw an arrow aiming right or aiming down at random. We put a robot on the upper left corner and let it move along the chessboard in the directions of the arrows. What is the probability that it will exit the chessboard from the square in the lower right corner?
\frac{5}{16}=\frac{\binom{6}{3}}{2^6}
39 J / 29 S
Write in the basic form (i.e. as the fraction \frac{a}{b}, where a and b are positive integers with no common divisor).
\frac{70}{37}
40 J / 30 S
Let ABCD be a rectangle with side lengths AB=30 and BC=20. For how many points X on its side AB is the perimeter of the triangle CDX an integer?
13
41 J / 31 S
In what order should we place the rows r_1, \dots, r_{11} of the table in the picture, if we want the newly created table to be symmetric with respect to the marked diagonal? It is sufficient to find one solution.

in the reverse order (eventually complemented by a circular shift), i.e. r_{11},r_{10},r_9,\dots,r_1 or r_{10},r_9,\dots,r_1,r_{11}, …, r_1,r_{11},r_{10},\dots, r_2
42 J / 32 S
For every positive integer n let Find the smallest integer k\geq 2 such that a_2\cdot a_3 \cdots a_k>4.
254
43 J / 33 S
Barbara cut the pizza into n equal slices and then she labeled them with numbers 1,2,\dots,n (she used each number exactly once). The numbering had the property that between each two slices with consecutive numbers (i and i+1) there was always the same number of other slices. Then came the fatty Paul and ate almost the whole pizza, only the three neighboring slices with numbers 11, 4, and 17 (in this exact order) remained. How many slices did the pizza have?
20
44 J / 34 S
In one of the lecture halls at Matfyz the seats are arranged in a rectangular grid. During the lecture of analysis there were exactly 11 boys in each row and exactly 3 girls in each column. Moreover, two seats were empty. What is the smallest possible number of the seats in the lecture hall?
144
45 J / 35 S
Circle k with radius 3 is internally tangent to circle l with radius 4 at point T. Find the greatest possible area of triangle TKL, where K \in k and L \in l.
9\sqrt3= \frac{27}{\sqrt{3}}
46 J / 36 S
Alice and Bob are playing the following game: At the beginning they have a set of numbers \{0, 1, \dots, 1024\}. First Alice removes any 2^9 elements, then Bob removes any of the remaining 2^8 elements, then Alice removes 2^7 elements and so on until at last Bob removes one element and there are exactly two numbers remaining. The game ends then and Alice pays to Bob the absolute value of the difference of these two numbers in Czech crowns. How many crowns will Bob get if they both play in the best way they can?
32
47 J / 37 S
Some students of Matfyz did not pass the exams and were expelled. They all started to study at SOU (some other university). It had the following consequences:
- The number of students of Matfyz decreased by one sixth.
- The number of students of SOU increased by one third.
- The average IQ on both schools increased by 2%.
How many times was the average IQ at Matfyz higher than average IQ at SOU?
\frac65 = 1.2-times
48 J / 38 S
A regular tetradecagon A_1A_2\dots A_{14} is inscribed in a circle k of radius 1. How large is the part of the disc circumscribed by the circle k, which lies inside the angle \angle A_1A_4A_{14}?
\frac{\pi}{14}
49 J / 39 S
Bill and Carol saw the 24-element set \{1, 2, \ldots, 24\}. Bill wrote down all its 12-element subsets whose sum of the elements was even. Carol wrote down all its 12-element subsets whose sum of the elements was odd. Who wrote more subsets and by how many?
Bill, \binom{12}6 = 924 subsets more
50 J / 40 S
Jack thought of three distinct positive integers a, b, c such that the sum of two of them was 800. When he wrote numbers a, b, c, a+b-c, a+c-b, b+c-a and a+b+c on a sheet of paper, he realized that all of them were primes. Determine the difference between the largest and the smallest number on Jack’s paper.
1594
51 J / 41 S
Helen stained two randomly chosen places on a one-meter bar. Thereupon Alex came and shattered the bar, just as well randomly, into 2013 pieces. What is the probability of both stains being now on the same piece?
\frac1{1007}
52 J / 42 S
How many ten-digit positive integers that are made up of 0,1,\dots ,9 (i.e. each digit is used exactly once) are multiples of 11 111?
Note: The first digit of a positive integer cannot be 0.
3456 = 2^5\cdot 5! - 2^4\cdot 4!
53 J / 43 S
A polynomial P(x) of degree 2013 with real coefficients fulfills for n=0,1,\dots,2013 the relation P(n)=3^n. Evaluate P(2014).
3^{2014}-2^{2014}
54 J / 44 S
Inside an isosceles triangle ABC fulfilling AB=AC and \angle BAC=99.4^\circ, a point D is given such that AD=DB and \angle BAD=19.7^\circ. Compute \angle BDC.
149.1^\circ
55 J / 45 S
Find the largest positive integer not ending with a zero such that removal of one of its “inner” digits produces its divisor.
Note: An “inner” digit denotes any digit except for the first and the last one.
180625
56 J / 46 S
Three mutually distinct real numbers a, b, c satisfy Compute the product abc.
3
57 J / 47 S
In a scalene triangle ABC, there is an altitude of the same length as one median and another altitude of the same length as another median. In what ratio are the lengths of the third altitude and the third median?
\frac{2}{7}