1 J
Wenn bekannt ist, dass es genau eine Möglichkeit gibt, 2013 als Summe zweier Primzahlen zu schreiben, was ist dann das Produkt dieser zwei Primzahlen?
4022
2 J
Zwei Kreise mit Radius 1 schneiden sich wie in der Abbildung. Dabei ist die Fläche, auf der sich die beiden Kreise überlappen, genau so groß wie die Fläche der beiden äußeren Sicheln. Wie groß ist die Fläche, auf der sich die Kreise überlappen?
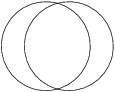
\frac{2}{3}\pi
3 J
Gegeben seien fünf gelbe Nadeln, vier rote, drei grüne und zwei blaue sowie eine orangefarbige Nadel. Auf wie viele Arten kann man diese so in dem abgebildeten Dreiecksgitter anordnen, dass keine zwei Nadeln mit der gleichen Farbe in der gleichen Reihe oder in der gleichen Spalte sind? Dabei sind Nadeln gleicher Farbe nicht unterscheidbar.

1
4 J
Bestimme die kleinste positive ganze Zahl, deren Querprodukt (= Produkt der Ziffern) genau 600 beträgt.
3558
5 J
Die positiven reellen Zahlen a und b erfüllen die Gleichungen Welchen Wert hat dann ab+\dfrac{1}{ab}?
33
6 J
Benedikt denkt sich eine sechsstellige Zahl, welche die folgenden Bedingungen erfüllt:
- Die Zahl ist eine Palindromzahl, d.h. eine Zahl, die von links und rechts gelesen den gleichen Wert hat.
- Die Zahl ist durch 9 teilbar.
- Streicht man die erste und die letzte Ziffer, so ist 11 der einzige Primfaktor der verbleibenden vierstelligen Zahl.
Wie lautet Benedikts Zahl?
513315
7 J
Der Punkt D liegt auf dem Durchmesser AB des Halbkreises k. Das Lot durch D auf AB schneidet k in C. Die Längen der Kreisbögen AC und CB verhalten sich wie 1:2. Bestimme das Verhältnis \overline{AD} : \overline{DB}.
1:3
8 J
Die zwei verwöhnten Brüder Valentin und Michael bekamen eine Packung Schokoladenkekse, die sie gerecht untereinander aufteilten. Beide aßen jeweils 2 oder 3 Schokoladenkekse pro Tag von ihrem Anteil. Valentins Kekse reichten ihm für genau 14 Tage und Michaels Kekse reichten ihm für genau drei Wochen. Wie viele Schokoladenkekse waren in der Packung?
84
9 J
Auf wie viele Arten kann man das Wort Náboj in dem Diagramm lesen?
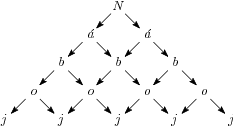
16
10 J
Die Bewohner einer Insel sind entweder konsequente Lügner oder sagen immer die Wahrheit. Genau 12 Inselbewohner sitzen an einem runden Tisch und behaupten alle, dass sie selbst immer die Wahrheit sagen und dass ihr rechter Nachbar ein Lügner ist. Wie viele Lügner können maximal in solch einer Anordnung sein?
6
11 J / 1 S
Katharina hat elf kongruente Quadrate, von denen sechs rot, drei blau und zwei grün sind. Wie viele Möglichkeiten gibt es, mit neun dieser elf Quadrate ein 3 \times 3-Quadrat zu bilden, so dass die Färbung erhalten bleibt, wenn man das 3 \times 3-Quadrat um 90^\circ im Uhrzeigersinn dreht? Dabei sollen Quadrate mit der gleichen Farbe nicht unterscheidbar sein.
0
12 J / 2 S
Auf einer Insel sind zwei Fünftel der Männer und drei Fünftel der Frauen verheiratet. Wie viel Prozent der Inselbewohner sind verheiratet?
48 \%=\frac{12}{25}
13 J / 3 S
Aus einem rechteckigen Blatt Papier mit den Seitenlängen 21 \text{cm} und 29{,}7 \text{cm} wird ein gleichseitiges Dreieck ausgeschnitten. Wie groß kann dessen Seitenlänge maximal sein?
14\sqrt3 = \frac{42}{\sqrt{3}}\,\text{cm}
14 J / 4 S
Daniela hat ein quadratisches Blatt Papier vier Mal nacheinander jeweils in der Mitte gefaltet, so dass sie nach jeder Faltung ein gleichschenkliges rechtwinkliges Dreieck hatte. Wie viele Quadrate kann man sehen, wenn man das Papier wieder entfaltet?
10
15 J / 5 S
Wie viele Fünfecke gibt es in der abgebildeten Figur?
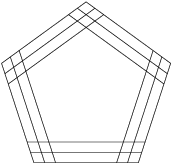
3^5=243
16 J / 6 S
Julian wollte zwei positive Zahlen addieren, hat aber aus Versehen eine Null ans Ende von einer der beiden Zahlen geschrieben. Als Ergebnis erhielt er 3858 anstatt des korrekten Resultats 2013. Bestimme die größere der beiden Zahlen.
1808
17 J / 7 S
Wie groß ist der Radius des kleinsten Kreises, der ein Dreieck mit den Seitenlängen 3, 5 und 7 überdecken kann?
3{,}5=\frac 72
18 J / 8 S
Lukas, Martin, Paul und Viktor haben zusammen 100 Lollipops. Je zwei von ihnen haben zusammen mindestens 41 Lollipops. Was ist die kleinste Anzahl an Lollipops, die Paul haben kann?
12
19 J / 9 S
Die Fläche eines Rechtecks ABCD sei 80 und die Länge einer Diagonalen 16. Bestimme den Sinus des spitzen Winkels zwischen den Diagonalen.
\frac58 = 0{,}625
20 J / 10 S
Was ist der größtmögliche Wert, den der Term a^b + c^d annehmen kann, wenn a, b, c und d verschiedene Elemente aus der Menge \{-7, -5, -4, -3, -2, -1\} sind?
(-1)^{-4}+(-3)^{-2}=\frac{10}{9}
21 J / 11 S
Ein Winkel der Größe 110^\circ wird zufällig in ein ebenes Koordinatensystem gezeichnet. Wie groß ist die Wahrscheinlichkeit dafür, dass seine beiden Schenkel den Graph einer Funktion darstellen?
\frac{11}{18}
22 J / 12 S
Josef hat am Tag des letztjährigen Náboj, das war der 23. März 2012, ein regelmäßiges 100-Eck A_1A_2 \dots A_{100}, das er im Uhrzeigersinn durchnummeriert hat, gezeichnet und auf eine beliebige Ecke einen Spielstein gelegt. An jedem folgenden Tag hat er den Spielstein um so viele Ecken im Uhrzeigersinn verschoben, wie die Nummer der aktuellen Ecke anzeigt (von A_3 würde er beispielsweise den Spielstein auf A_6 verschieben oder von A_{96} auf A_{92}). Jetzt liegt der Spielstein auf der Ecke A_{100}. Wie groß ist die Wahrscheinlichkeit für dieses Ereignis?
0{,}04=\frac1{25}
23 J / 13 S
Positive ganze Zahlen, die als Differenz zweier Quadratzahlen dargestellt werden können, sollen subtraktiv genannt werden. Wie viele der Zahlen 1,2, \dots, 2013 sind subtraktiv?
1510
24 J / 14 S
Drei sich nicht überschneidende regelmäßige Vielecke mit Seitenlänge 1 haben einen gemeinsamen Eckpunkt A. Der Rand der Vereinigung ihrer Flächen bildet einen (nicht konvexen) Polygonzug M, der den Punkt A im Inneren haben soll (d.h. A liegt nicht auf dem Rand von M). Bestimme die Länge von M, wenn eines der regelmäßigen Vielecke ein Quadrat und ein weiteres ein regelmäßiges Sechseck ist.
16
25 J / 15 S
Veronika hat die Zahlen von 1 bis 100 in beliebiger Reihenfolge nebeneinander geschrieben. Was ist die Wahrscheinlichkeit dafür, dass für jedes i = 1,\dots,50 die Zahl an der Stelle 2i-1 kleiner ist als die Zahl an der Stelle 2i?
2^{-50}
26 J / 16 S
Die Farbe Pink wird aus den Farben Rot und Weiß im Verhältnis 1:1 gemischt und die Farbe Cyan aus Blau und Weiß im Verhältnis 1:2. Simone will ihr Zimmer mit einer Farbe streichen, die aus Pink und Cyan im Verhältnis 2:1 besteht. Sie hat bereits drei Dosen blaue Farbe mit einer Dose roter Farbe vermischt. Wie viele Dosen muss sie zu dieser Mischung noch hinzufügen, wenn nur noch Dosen mit roter und weißer Farbe übrig sind?
23
27 J / 17 S
Ein Zauberer hat einen Hut mit mehreren weißen, grauen und schwarzen Hasen. Am Anfang, wenn er beginnt sie zufällig aus dem Hut zu ziehen (ohne sie zurückzulegen), beträgt die Wahrscheinlichkeit, dass er einen weißen Hasen vor einem grauen zieht, genau \frac34. Die Wahrscheinlichkeit, dass er einen grauen Hasen vor einem schwarzen zieht, ist ebenfalls \frac34. Wie groß ist die Wahrscheinlichkeit, dass er am Anfang einen weißen vor einem schwarzen Hasen zieht?
\frac{9}{10}
28 J / 18 S
Die positiven ganzen Zahlen a und b erfüllen die Gleichung 49a+99b = 2013. Bestimme a+b.
37
29 J / 19 S
In die Ecken des Quadrats PQRS mit der Seitenlänge 6\,\text{cm} werden wie in der Abbildung vier kleinere Quadrate mit der Seitenlänge 2\,\text{cm} einbeschrieben. Diejenigen Ecken dieser Quadrate, die im Inneren des großen Quadrates liegen, seien mit W, X, Y und Z bezeichnet. Ein Quadrat ABCD wird nun so konstruiert, dass die Punkte W, X, Y bzw. Z jeweils auf den Seiten AB, BC, CD bzw. DA liegen. Bestimme den größtmöglichen Abstand zwischen den Punkten P und D.
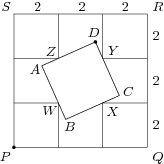
6\,\text{cm}
30 J / 20 S
In zwanzig Kisten mit Äpfeln befinden sich insgesamt 129 Äpfel. In einigen der Kisten sind genau 4 Äpfel und alle übrigen Kisten enthalten genau x Äpfel. Bestimme alle möglichen Werte für x.
11, 53
31 J / 21 S
Gegeben seien zwei reelle Zahlen a und b mit a > b > 0, die die Gleichung erfüllen. Bestimme den Wert von \dfrac{a+b}{a-b}.
\sqrt{\frac{2015}{2011}}
32 J / 22 S
Die Zahlen von 1 bis 7 sollen so in die Felder des abgebildeten Heptominos gefüllt werden, dass die Summe in der Zeile unten gleich der Summe in der Spalte links ist. Dabei darf jede der Zahlen nur einmal verwendet werden. Wie viele Möglichkeiten gibt es dafür?
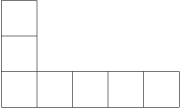
144=3 \cdot 2 \cdot 4!
33 J / 23 S
Das Dreieck \triangle ABC sei spitzwinklig mit \overline{AB}=4\pi, \overline{BC}=4\pi+3 und \overline{CA}=4\pi+6. Der Höhenfußpunkt der Höhe von A auf BC sei D. Bestimme \overline{CD}-\overline{BD}.
12
34 J / 24 S
In Sikinien fahren Straßenbahnen den ganzen Tag in gleichen zeitlichen Abständen und das in beide Richtungen. Ein Fußgänger, der an den Gleisen entlang geht, wird alle 12 Minuten von einer Straßenbahn überholt und alle 4 Minuten kommt ihm eine entgegen. In welchem zeitlichen Abstand fahren die Straßenbahnen?
6 Minuten
35 J / 25 S
Wie viele nicht entartete Dreiecke kann man bilden, wenn man jeweils drei beliebige Punkte aus der Abbildung verbindet?
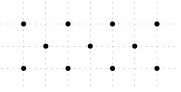
Hinweis: Die Punkte sind auf dem angedeuteten Gitter angeordnet.
148=\binom{11}{3}-17
36 J / 26 S
Martin hat eine Schachtel Pralinen geschenkt bekommen, in der 30 Pralinen in drei Reihen zu je zehn angeordnet sind. Er isst die Pralinen eine nach der anderen so, dass sich die Anzahlen der Pralinen in jeweils zwei Reihen um höchstens Eins unterscheiden. Wie viele Möglichkeiten hat er, die Schachtel zu leeren?
6^{10}\cdot (10!)^3
37 J / 27 S
Eine positive sechsstellige Zahl wird verdoppelt genannt, wenn die ersten drei Ziffern mit den letzten drei Ziffern identisch sind, und zwar in derselben Reihenfolge. Beispielsweise ist 227227 verdoppelt, aber 135153 nicht. Wie viele sechsstellige verdoppelte Zahlen sind durch 2013 teilbar?
Hinweis: Die führende Ziffer darf nicht 0 sein.
5
38 J / 28 S
Auf jedes Feld eines 4\times 4-Schachbretts zeichnet man zufällig entweder einen Pfeil nach unten oder einen Pfeil nach rechts. In die linke obere Ecke des Schachbretts setzt man nun einen Roboter, der sich entsprechend der Pfeilrichtungen auf dem Brett bewegt bis er es verlässt. Wie groß ist die Wahrscheinlichkeit dafür, dass der Roboter das Schachbrett von der rechten unteren Ecke aus verlassen wird?
\frac{5}{16}=\frac{\binom{6}{3}}{2^6}
39 J / 29 S
Schreibe den Bruch in seiner gekürzten Form, das heißt, als Bruch \frac{a}{b} mit ganzen positiven Zahlen a und b, die teilerfremd sind.
\frac{70}{37}
40 J / 30 S
Gegeben sei ein Rechteck ABCD mit den Seitenlängen \overline{AB}=30 und \overline{BC}= 20. Für wie viele Punkte X auf der Seite AB ist der Umfang des Dreiecks \triangle CDX ganzzahlig?
13
41 J / 31 S
In welche Reihenfolge muss man die Zeilen r_1, \dots, r_{11} der Tabelle in der folgenden Abbildung bringen, wenn man will, dass die neu entstandene Tabelle bezüglich der markierten Diagonale symmetrisch sein soll? Es genügt, eine Lösung anzugeben.

In umgekehrte Reihenfolge (ggf. noch zyklisch vertauscht), das heißt [r_{11},r_{10},r_9,\dots,r_1] oder [r_{10},r_9,\dots,r_1,r_{11}], …, [r_1,r_{11},r_{10},\dots, r_2]
42 J / 32 S
Für jede positive ganze Zahl n sei a_n definiert durch Finde die kleinste natürliche Zahl k\geq 2 mit der Eigenschaft a_2 a_3\cdots a_k >4.
254
43 J / 33 S
Katrin hat eine Pizza in n gleiche Stücke geschnitten und diese mit je einer der Zahlen 1, 2, \ldots, n gekennzeichnet. Die Nummerierung hatte die Eigenschaft, dass zwischen je zwei Pizzastücken mit aufeinander folgenden Zahlen i und i+1 immer die gleiche Anzahl an Pizzastücken vorhanden war. Dann ist der dicke Lukas gekommen und hat fast die ganze Pizza aufgegessen. Was er davon übrig gelassen hat, waren drei direkt nebeneinander liegende Pizzastücke mit den Nummern 11, 4 und 17 genau in dieser Reihenfolge. Wie viele Stücke hatte die Pizza?
20
44 J / 34 S
In einem Hörsaal an der Mathfyz-Universität sind die Sitzplätze in einem rechteckigen Gitter angeordnet. In der Analysis-Vorlesung saßen genau 11 Studenten in jeder Zeile und genau 3 Studentinnen in jeder Spalte. Zwei Sitzplätze blieben leer. Was ist die kleinstmögliche Anzahl an Sitzplätzen in diesem Hörsaal?
144
45 J / 35 S
Gegeben sei ein Kreis l mit Radius 4 und ein zweiter Kreis k mit Radius 3, der im Inneren von l liegt und l genau im Punkt T berührt. Finde den größtmöglichen Flächeninhalt eines Dreiecks \triangle TKL, wobei K ein Punkt auf k und L ein Punkt auf l ist.
9\sqrt3= \frac{27}{\sqrt{3}}
46 J / 36 S
Lukas und Viktor spielen das folgende Spiel: Am Anfang steht ihnen die Menge der Zahlen \{0,1,2,\ldots,1024\} zur Verfügung. Als Erster entfernt Lukas irgendwelche 2^9 Zahlen aus der gegebenen Menge. Von den restlichen Zahlen nimmt Viktor nun 2^8 Stück weg, anschließend ist wieder Lukas an der Reihe und entfernt 2^7 Zahlen. Das geht abwechselnd so weiter bis schließlich Viktor ein Element entfernt, so dass noch genau zwei Zahlen übrig bleiben. Das Spiel ist nun beendet und Lukas muss an Viktor den Absolutbetrag der Differenz der beiden übrig gebliebenen Zahlen in tschechischen Kronen bezahlen. Wie viele Kronen wird Viktor bekommen, vorausgesetzt, dass beide Spieler jeweils für sich optimal spielen?
32
47 J / 37 S
Einige Studenten der Mathfyz-Universität schafften ihre Prüfungen nicht und wechselten deshalb an die IAU (Irgendeine Andere Universität). Dieser Wechsel hatte die folgenden Konsequenzen:
- Die Zahl der Studenten an der Mathfyz-Uni verringerte sich um ein Sechstel.
- Die Zahl der Studenten an der IAU stieg um ein Drittel.
- Der durchschnittliche Intelligenzquotient (IQ) stieg an beiden Universitäten um 2 %.
Um welchen Faktor war der durchschnittliche IQ der Studenten an der Mathfyz-Uni höher als der durchschnittliche IQ der Studenten an der IAU?
\frac65 = 1{,}2-mal
48 J / 38 S
Ein reguläres 14-Eck A_1A_2\dots A_{14} ist einem Kreis k mit Radius 1 einbeschrieben. Wie groß ist das Flächenstück, das vom Kreis sowie von den Sehnen A_1A_4 und A_4A_{14} begrenzt wird?
\frac{\pi}{14}
49 J / 39 S
Emil und Martina betrachten die 24-elementige Menge \{1, 2, \ldots, 24\}. Emil schreibt alle 12-elementigen Teilmengen auf, bei denen die Summe aller Elemente gerade ist. Martina schreibt alle 12-elementigen Teilmengen auf, bei denen die Summe aller Elemente ungerade ist. Wer schreibt mehr Teilmengen auf und wie viele mehr?
Emil, \binom{12}6 = 924 Teilmengen mehr
50 J / 40 S
Ferdinand denkt sich drei paarweise verschiedene positive ganze Zahlen a, b und c aus, so dass die Summe von zwei dieser Zahlen genau 800 ist. Als er dann die Zahlen a, b, c, a+b-c, a+c-b, b+c-a und a+b+c auf ein Blatt Papier schreibt, stellt er fest, dass alle prim sind. Wie groß ist die Differenz zwischen der größten und der kleinsten Zahl auf dem Papier?
1594
51 J / 41 S
Hannah markiert zufällig zwei Stellen auf einem Stab, der einen Meter lang ist. Danach zerbricht Peter den Stab, wiederum zufällig, in 2013 Stücke. Wie groß ist die Wahrscheinlichkeit, dass sich die zwei Markierungen auf demselben Stück befinden?
\frac1{1007}
52 J / 42 S
Wie viele zehnstellige positive ganze Zahlen, die jede der Ziffern 0,1,\dots ,9 genau einmal enthalten, sind Vielfache von 11 111?
Hinweis: Positive ganze Zahlen beginnen nicht mit einer Null.
3456 = 2^5\cdot 5! - 2^4\cdot 4!
53 J / 43 S
Für ein Polynom P(x) vom Grad 2013 mit reellen Koeffizienten gilt für alle n=0,1,\dots,2013 die Gleichnung P(n)=3^n. Bestimme P(2014).
3^{2014}-2^{2014}
54 J / 44 S
Im gleichschenkligen Dreieck \triangle ABC mit \overline{AB}=\overline{AC} und \angle BAC=99.4^\circ ist ein Punkt D gegeben mit \overline{AD}=\overline{DB} und \angle BAD=19.7^\circ. Wie groß ist \angle BDC?
149{,}1^\circ
55 J / 45 S
Finde die größte positive ganze Zahl, die nicht auf null endet und die Eigenschaft hat, dass das Entfernen einer bestimmten „inneren“ Ziffer einen Teiler der Zahl liefert.
Hinweis: Eine „innere“ Ziffer ist jede Ziffer außer der ersten und der letzten.
180625
56 J / 46 S
Drei paarweise verschiedene reelle Zahlen a, b und c erfüllen Bestimme das Produkt abc.
3
57 J / 47 S
Im nicht gleichschenkligen Dreieck \triangle ABC gibt es eine Höhe und eine Seitenhalbierende der gleichen Länge, sowie eine andere Höhe mit der selben Länge einer anderen Seitenhalbierenden. Welches Verhältnis haben die Längen der dritten Höhe und der dritten Seitenhalbierenden?
\frac{2}{7}























