1 J
Je známo, že číslo 2013 se dá právě jedním způsobem zapsat jako součet dvou prvočísel. Čemu je roven jejich součin?
4022
2 J
Dvě kružnice o poloměru 1 se protínají tak, že obsah prostřední části je roven součtu obsahů krajních dvou. Čemu je roven obsah prostřední části?
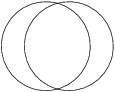
\frac23\pi
3 J
Máme pět žlutých kolíků, čtyři červené, tři zelené, dva modré a jeden oranžový. Kolika způsoby je můžeme rozmístit do trojúhelníkové sítě (viz obrázek) tak, aby v žádném řádku ani sloupci nebyly dva kolíky stejné barvy? Stejně barevné kolíky považujeme za nerozlišitelné.

1
4 J
Najděte nejmenší přirozené číslo, jehož součin cifer je roven 600.
3558
5 J
Kladná reálná čísla a, b splňují Čemu je rovna hodnota výrazu ab+\frac{1}{ab}?
33
6 J
Míša objevila šesticiferné přirozené číslo splňující následující podmínky:
- Číslo se čte stejně zleva doprava i zprava doleva.
- Je dělitelné devíti.
- Po škrtnutí první a poslední cifry je jediným prvočíselným dělitelem nového čísla číslo 11.
Které číslo Míša objevila?
513315
7 J
Na průměru AB půlkružnice k je dán bod D. Kolmice k AB vedená bodem D protne půlkružnici k v bodě C. Jsou-li délky oblouků AC a CB půlkružnice k v poměru 1 : 2, určete hodnotu poměru |AD| : |DB|.
1 : 3
8 J
Dva rozmazlení bratříčci Viktor a Mišo dostali pytel bonbonů, který si půl na půl rozdělili. Každý z nich sní během dne dva až tři bonbony. Malému Vikouškovi bonbony vydržely na čtrnáct dní, staršímu Mišovi přesně na tři týdny. Kolik bonbonů bylo původně v pytli?
84
9 J
Kolika způsoby lze ve schématu na obrázku přečíst slovo Náboj?
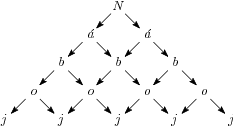
16
10 J
Na ostrově žijí obyvatelé dvou typů: pravdomluvní vždy říkají pravdu, lháři zásadně lžou. Dvanáct obyvatel ostrova se posadilo do kruhu. Všichni svorně tvrdí, že jsou pravdomluvní. Také tvrdí, že po jejich pravé ruce sedí lhář. Kolik nejvíce lhářů může být mezi těmito dvanácti lidmi?
6
11 J / 1 S
Helča má jedenáct shodných čtvercových dlaždiček – šest červených, tři modré a dvě zelené. Kolika způsoby může z některých devíti z nich sestavit tabulku 3\times 3, musí-li obarvení tabulky zůstat zachováno, otočíme-li ji o 90^\circ po směru hodinových ručiček? Stejně barevné dlaždičky považujeme za nerozlišitelné.
0
12 J / 2 S
Na ostrově jsou ženaté dvě pětiny mužů a vdané tři pětiny žen. Kolik procent obyvatelstva ostrova žije v manželství?
48 \%=\frac{12}{25}
13 J / 3 S
Jaká je délka strany největšího rovnostranného trojúhelníku, který lze vystřihnout z obdélníkového papíru o rozměrech 21 \times 29{,}7\,\text{cm}?
14\sqrt3 = \frac{42}{\sqrt{3}}\,\text{cm}
14 J / 4 S
Dáška si vzala čtvercový kus papíru a složila ho čtyřikrát na polovinu bez zpětného rozkládání tak, že každým složením vytvořila rovnoramenný pravoúhlý trojúhelník. Kolik čtverců je vidět po rozložení papíru?
10
15 J / 5 S
Kolik pětiúhelníků se nachází na obrázku?
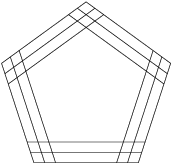
3^5=243
16 J / 6 S
Při sčítání dvou přirozených čísel Kája omylem za jedno z nich připsala nulu, a tak jí vyšlo 3858 místo 2013. Čemu je rovno větší z čísel, která měla Kája sečíst?
1808
17 J / 7 S
Jaký poloměr má nejmenší kruh, jímž lze zakrýt trojúhelník se stranami délek 3, 5 a 7?
3{,}5
18 J / 8 S
Kuba, Mirek, \pitr a Vejtek mají dohromady 100 lízátek. Přitom každí dva z nich mají dohromady lízátek alespoň 41. Kolik nejméně lízátek může mít \pitr?
12
19 J / 9 S
Šavlík si nakreslil obdélník ABCD s obsahem 80 a s délkou úhlopříčky 16. Čemu je roven sinus ostrého úhlu svíraného úhlopříčkami obdélníku?
\frac58 = 0{,}625
20 J / 10 S
Jakou největší hodnotu může mít výraz a^b + c^d, jsou-li a, b, c, d navzájem různá čísla z množiny \{-7, -5, -4, -3, -2, -1\}?
(-1)^{-4}+(-3)^{-2}=\frac{10}{9}
21 J / 11 S
Do roviny s kartézskou soustavou souřadnic jsme náhodně umístili úhel o velikosti 110^\circ. Jaká je pravděpodobnost, že ramena tohoto úhlu tvoří graf funkce?
\frac{11}{18}
22 J / 12 S
Pepa si v den konání loňského Náboje (23. března 2012) nakreslil pravidelný stoúhelník A_1A_2\dots A_{100} (číslovaný po směru chodu hodinových ručiček) a na jeden náhodný vrchol položil žeton. Každé další ráno pak žeton posunul o tolik vrcholů po směru chodu hodinových ručiček, jaké bylo číslo vrcholu, na kterém žeton zrovna ležel (z vrcholu A_3 by se tedy například žeton přesunul na A_6, z vrcholu A_{96} na A_{92}). Teď leží žeton na vrcholu A_{100}. Jaká byla pravděpodobnost, že se něco takového stane?
0{,}04=\frac1{25}
23 J / 13 S
Přirozeným číslům, která se dají zapsat jako rozdíl druhých mocnin dvou celých čísel, říkejme rozdílová. Kolik z čísel 1,2,\dots, 2013 je rozdílových?
1510
24 J / 14 S
Tři pravidelné nepřekrývající se mnohoúhelníky o stranách délek 1 se stýkají v bodě A tak, že tvoří (nekonvexní) mnohoúhelník M, jemuž je A vnitřním bodem. Je-li jeden z pravidelných mnohoúhelníků šestiúhelník a druhý čtverec, určete obvod mnohoúhelníku M.
16
25 J / 15 S
Martin napsal na papír čísla 1 až 100 v náhodném pořadí. Jaká je pravděpodobnost, že pro každé i=1,\dots, 50 je to (2i-1)-té menší než to (2i)-té?
2^{-50}
26 J / 16 S
Růžová barva vznikne smícháním červené a bílé v poměru 1:1, azurová vznikne z modré a bílé v poměru 1:2. Anička si chce vymalovat pokoj barvou, která vznikne z růžové a azurové smíchané v poměru 2:1. Zatím smíchala tři plechovky modré a jednu plechovku červené barvy. Zbývají jí už jen plechovky s červenou a bílou barvou. Kolik celkem plechovek ještě musí přidat?
23
27 J / 17 S
V klobouku je několik bílých, šedých a černých králíků. Je známo, že když kouzelník začne králíky postupně náhodně vytahovat (aniž by je vracel), je pravděpodobnost, že vytáhne dřív bílého králíka než šedého, rovna \frac34. Podobně je pravděpodobnost, že vytáhne dřív šedého králíka než černého, rovna \frac34. Jaká je pravděpodobnost, že vytáhne dřív bílého králíka než černého?
\frac{9}{10}
28 J / 18 S
Pro přirozená čísla a, b platí 49a+99b = 2013. Určete hodnotu součtu a+b.
37
29 J / 19 S
V rozích čtverce PQRS o straně délky 6\,\text{cm} jsou umístěny čtyři menší čtverce o stranách délek 2\,\text{cm}. Označme jejich vrcholy W, X, Y, Z jako na obrázku. Čtverec ABCD je sestrojený tak, že body W, X, Y, Z leží uvnitř jeho stran AB, BC, CD, DA. Určete největší možnou vzdálenost bodů P a D.
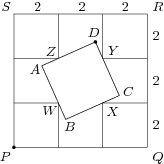
6
30 J / 20 S
Ve dvaceti krabicích je dohromady 129 jablek. Přitom v několika krabicích je přesně po čtyřech jablkách a ve zbylých po x jablkách. Nalezněte všechny možné hodnoty x.
11, 53
31 J / 21 S
Kladná reálná čísla a, b splňují a > b a současně Čemu se rovná hodnota výrazu \frac{a+b}{a-b}?
\sqrt{\frac{2015}{2011}}
32 J / 22 S
Kolika způsoby lze do různých políček heptomina na obrázku vyplnit čísla 1 až 7 (každé musíme použít právě jednou), aby byl součet čísel ve spodním řádku stejný jako součet čísel v levém sloupci?
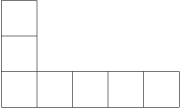
144=3 \cdot 2 \cdot 4!
33 J / 23 S
Délky stran ostroúhlého trojúhelníku ABC splňují |AB|=4\pi, |BC|=4\pi+3, |CA|=4\pi+6. Označme D patu výšky z vrcholu A. Určete |CD|-|BD|.
12
34 J / 24 S
Tramvaje mají celý den v obou směrech trasy stejné intervaly. Chodec, který šel podél dráhy tramvaje, pozoroval, že ho každých 12 minut jedna tramvaj předjede a zároveň ho každé 4 minuty mine tramvaj v protisměru. Jaký interval mají tramvaje?
6 minut
35 J / 25 S
Kolik nedegenerovaných trojúhelníků může být vytvořeno spojením některých tří bodů na obrázku?
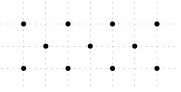
Poznámka: Body jsou zarovnány do naznačené mřížky.
148=\binom{11}{3}-17
36 J / 26 S
Filip dostal bonboniéru se třiceti bonbóny uspořádanými ve třech řádcích po deseti. Aby si ji náležitě vychutnal, jí bonbóny po jednom, a to tak, aby se počty zbývajících bonbónů v každých dvou řádcích v každý okamžik lišily nejvýše o jedna. Kolika způsoby může bonboniéru sníst?
6^{10}\cdot (10!)^3
37 J / 27 S
Řekneme, že šesticiferné přirozené číslo je dvojité, pokud se jeho první tři cifry (v tomto pořadí) shodují s jeho dalšími třemi ciframi (tedy například číslo 227227 je dvojité, zatímco číslo 135153 dvojité není). Kolik dvojitých čísel je beze zbytku dělitelných číslem 2013?
Poznámka: Přirozené číslo nemůže začínat nulou.
5
38 J / 28 S
Na každé políčko hracího plánu 4\times 4 náhodně nakreslíme šipku doprava nebo dolů a na levé horní políčko postavíme robota. Robot se vždy posouvá na sousední políčko ve směru šipky. Jaká je pravděpodobnost, že robot opustí hrací plán krokem z pravého dolního políčka?
\frac{5}{16}=\frac{\binom{6}{3}}{2^6}
39 J / 29 S
Vyjádřete v základním tvaru (tj. jako zlomek \frac{a}{b}, kde a, b jsou nesoudělná přirozená čísla).
\frac{70}{37}
40 J / 30 S
Je dán obdélník ABCD s délkami stran |AB|=30, |BC|=20. Pro kolik bodů X na jeho straně AB platí, že trojúhelník CDX má celočíselný obvod?
13
41 J / 31 S
V jakém pořadí je potřeba uspořádat řádky r_1, \dots, r_{11} vyobrazené tabulky, aby vznikla tabulka symetrická podle vyznačené úhlopříčky? Stačí nalézt jedno řešení.

pozpátku s případnou cyklickou záměnou, tedy r_{11},r_{10},r_9,\dots,r_1 nebo r_{10},r_9,\dots,r_1,r_{11} atd. až r_1,r_{11},r_{10},\dots, r_2
42 J / 32 S
Pro každé přirozené číslo n položme Nalezněte nejmenší přirozené číslo k\geq 2 takové, že a_2\cdot a_3 \cdots a_k>4.
254
43 J / 33 S
Kikina připravila pizzu, rozkrájela ji na n stejných dílků a pak na ně připíchla lístky s čísly 1,2,\dots,n (každé číslo použila právě jednou) tak, že mezi dílky s po sobě jdoucími čísly byl vždy stejný počet jiných dílků. Poté přišel špekoun Lukáš a skoro celou pizzu snědl – zbyly jen tři sousední dílky s čísly 11, 4 a 17 (v tomto pořadí). Kolik dílků měla pizza původně?
20
44 J / 34 S
V jedné posluchárně na Matfyzu jsou místa k sezení uspořádaná do obdélníkové mřížky. Během jedné přednášky z analýzy sedělo v každé řadě přesně 11 chlapců, v každém sloupci seděla přesně 3 děvčata a ještě celkem dvě místa zůstala volná. Kolik nejméně míst může být v posluchárně?
144
45 J / 35 S
Kružnice k o poloměru 3 a kružnice l o poloměru 4 mají vnitřní dotyk v bodě T. Jaký největší obsah může mít trojúhelník TKL, jehož vrcholy K, L leží po řadě na kružnicích k, l?
9\sqrt3= \frac{27}{\sqrt{3}}
46 J / 36 S
Roman a Majkl hrají hru. Na začátku mají množinu \{0, 1, \dots, 1024\} a střídají se v tazích. Nejdřív Roman odebere libovolných jejích 2^9 prvků, pak odebere Majkl libovolných 2^8 prvků, pak Roman 2^7 prvků a tak dále, až nakonec odebere Majkl jeden prvek, takže v množině přesně dvě čísla zbydou. Tím hra končí a Roman zaplatí Majklovi absolutní hodnotu rozdílu těchto čísel v korunách. Kolik korun Majkl vyhraje, pokud oba hráči hrají nejlépe, jak mohou?
32
47 J / 37 S
Na Matfyzu vyhodili z analýzy několik studentů. Všichni tito studenti přestoupili na VŠN (vysokou školu nejmenovanou). To mělo následující důsledky:
- Počet studentů na Matfyzu se snížil o šestinu.
- Počet studentů na VŠN se zvýšil o třetinu.
- Na obou školách vzrostlo průměrné IQ o 2%.
Kolikrát je nyní průměrné IQ na Matfyzu vyšší než na VŠN?
\frac65 = 1{,}2-krát
48 J / 38 S
Do kružnice k o poloměru 1 je vepsán pravidelný čtrnáctiúhelník A_1A_2\dots A_{14}. Jaká je plocha té části kruhu vymezeného kružnicí k, která leží uvnitř ostrého úhlu A_1A_4A_{14}?
\frac{\pi}{14}
49 J / 39 S
Olin s Martinou uviděli 24-prvkovou množinu \{1, 2, \ldots, 24\}. Olin si vypsal všechny její dvanáctiprvkové podmnožiny, které mají sudý součet prvků, zato Martina si vypsala všechny dvanáctiprvkové podmnožiny s lichým součtem prvků. Kdo si vypsal víc množin a o kolik?
Olin o \binom{12}6 = 924
50 J / 40 S
Petr si myslí tři navzájem různá přirozená čísla a, b, c taková, že součet některých dvou z nich je 800. Když si na papír napsal čísla a, b, c, a+b-c, a+c-b, b+c-a a a+b+c, zjistil, že to jsou všechno prvočísla. Určete rozdíl největšího a nejmenšího čísla na Petrově papíře.
1594
51 J / 41 S
Alča na dvě náhodná místa metrové tyčky nakreslila puntíky. Pak přišel Pepa a tyčku náhodně rozlámal na 2013 částí. Jaká je pravděpodobnost, že oba puntíky jsou teď na té samé části?
\frac1{1007}
52 J / 42 S
Kolik deseticiferných přirozených čísel obsahujících každou z cifer 0,1,\dots ,9 právě jednou je násobkem čísla 11 111?
Poznámka: Přirozené číslo nemůže začínat nulou.
3456 = 2^5\cdot 5! - 2^4\cdot 4!
53 J / 43 S
Polynom P(x) stupně 2013 s reálnými koeficienty splňuje pro n=0,1,\dots,2013 vztah P(n)=3^n. Určete P(2014).
3^{2014}-2^{2014}
54 J / 44 S
Uvnitř rovnoramenného trojúhelníku ABC splňujícího |AB|=|AC| a |\uhel BAC|=99{,}4^\circ je dán bod D tak, že |AD|=|DB| a |\uhel BAD|=19{,}7^\circ. Určete |\uhel BDC|.
149{,}1^\circ
55 J / 45 S
Nalezněte největší přirozené číslo nekončící nulou takové, že škrtnutím některé jeho „vnitřní“ cifry získáme jeho dělitele.
Poznámka: „Vnitřní“ cifrou rozumíme každou cifru kromě první a poslední.
180625
56 J / 46 S
Pro navzájem různá reálná čísla a, b, c platí Čemu je roven součin abc?
3
57 J / 47 S
V různostranném trojúhelníku ABC má jedna výška stejnou délku jako jedna těžnice a jiná výška má stejnou délku jako jiná těžnice. V jakém poměru jsou délka třetí výšky a délka třetí těžnice?
\frac{2}{7}






















