1 J
2013 pontosan egyféleképpen írható fel két prím összegeként. Mennyi ennek a két prímnek a szorzata?
4022
2 J
Két egységsugarú kör metszi egymást. A körök metszetének területe megegyezik a körök metszeten kívüli részeinek területösszegével. Mekkora a metszet területe?
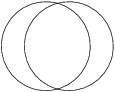
\frac23\pi
3 J
Van 5 sárga, 4 piros, 3 zöld, 2 kék és 1 lila rajzszögünk. Hányféleképpen tudjuk elhelyezni őket az ábrán látható háromszög alakú rácsban úgy, hogy egy sorban vagy oszlopban se legyenek azonos színű rajzszögek? (Az egyforma színű rajzszögek nem megkülönböztethetők).

1
4 J
Melyik a legkisebb pozitív egész szám, amelyben a számjegyek szorzata 600?
3558
5 J
Az a és b pozitív valós számokra teljesül, hogy Mennyi az ab+\frac{1}{ab} kifejezés értéke?
33
6 J
Lali leírt a füzetébe egy hatjegyű egész számot, amire teljesülnek az alábbi állítások:
- A számot visszafelé olvasva az eredeti számot kapjuk.
- A szám osztható 9-cel.
- Ha elhagyjuk a szám első és utolsó számjegyét, a megmaradó négyjegyű számnak csak egy prímosztója van, a 11.
Melyik számot írta le Lali?
513315
7 J
Egy k félkör AB átmérőjén rajta van a D pont. A D ponton keresztül merőlegest állítunk az AB átmérőre, és ez a merőleges a k félkört a C pontban metszi. Az AC és CB körívek hosszának aránya 1:2. Mekkora az AD : DB arány?
1 : 3
8 J
András és Béla kapnak egy zacskó cukorkát, és elosztják egymás közt úgy, hogy mindketten ugyanannyi darabot kapnak. Ezután mindketten megesznek naponta 2 vagy 3 darab cukorkát. Így András 14 nap alatt ette meg a cukorkáit, míg Béla pontosan három hét alatt. Hány cukorka volt a zacskóban?
84
9 J
Hányféleképpen olvasható ki a Náboj szó az ábrából?
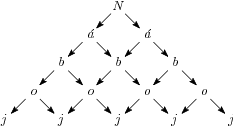
16
10 J
Egy sziget lakói vagy igazmondók, vagy hazudozók. Az igazmondók mindig igazat mondanak, a hazudozók pedig mindig hazudnak. 12 szigetlakó ül egy kerek asztal körül, és közülük mindenki azt állítja: "Én igazmondó vagyok, és a jobb oldali szomszédom hazudozó." Legfeljebb hány hazudozó ülhet az asztalnál?
6
11 J / 1 S
Julinak 11 egybevágó négyzet alakú csempéje van, amely közül 6 piros, 3 kék és 2 zöld. Hányféleképpen tud lefedni ezekkel egy 3 \times 3-as négyzetet 9 csempével úgy, hogy ha az óramutató járásával megegyező irányban 90^\circ-kal elforgatjuk a középpontja körül a négyzetet, akkor az elforgatott négyzet színezése megegyezik az eredeti színezéssel? (Az azonos színű csempék nem megkülönböztethetők.)
0
12 J / 2 S
Egy szigeten az ott élők közül a férfiak kétötöde és a nők háromötöde házas. A szigetlakók hány százaléka házas?
48 \%=\frac{12}{25}
13 J / 3 S
Legfeljebb mekkora oldalhosszúságú szabályos háromszöget tudunk kivágni egy 21 \times 29.7\,\text{cm} méretű téglalap alakú papírlapból?
14\sqrt3 = \frac{42}{\sqrt{3}}\,\text{cm}
14 J / 4 S
Kata egy négyzet alakú lapot négyszer egymás után félbehajt úgy, hogy minden hajtás után egy egyenlő szárú derékszögű háromszöget kap. Ezután kihajtogatja a lapot, és leteszi maga elé. Hány négyzetet láthat Kata az előtte lévő papíron?
10
15 J / 5 S
Hány ötszög látható az ábrán?
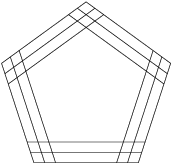
3^5=243
16 J / 6 S
Tibi össze akart adni két pozitív egészet, de véletlenül egy 0 számjegyet írt az egyik szám végére. Így 3858-at kapott összegként a helyes 2013 helyett. Mekkora a két szám közül a nagyobbik?
1808
17 J / 7 S
Mekkora a sugara a lehető legkisebb körnek, amivel le lehet fedni egy 3, 5, és 7 egység oldalhosszúságú háromszöget?
3.5
18 J / 8 S
Annának, Biának, Cilinek és Dórinak 100 nyalókája van együtt. Bármely két lánynak együtt legalább 41 nyalókája van. Legalább hány nyalókája van Annának?
12
19 J / 9 S
Egy ABCD téglalap területe 80 területegység, az átlója pedig 16 egység hosszú. Mekkora z átlók által bezárt szög szinusza?
\frac58 = 0.625
20 J / 10 S
Mekkora az a^b + c^d kifejezés lehető legnagyobb értéke, ha a, b, c, és d a halmaz különböző elemei?
(-1)^{-4}+(-3)^{-2}=\frac{10}{9}
21 J / 11 S
Egy 110^\circ-os szöget véletlenszerűen elhelyezünk a koordinátasíkon. Mekkora a valószínűsége, hogy a szög szárai egy függvénygrafikont alkotnak?
\frac{11}{18}
22 J / 12 S
Jancsi rajzolt egy A_1A_2 \dots A_{100} szabályos százszöget (az óramutató járása szerint számozva) a tavalyi Nábojon (2012. március 23.) és véletlenszerűen elhelyezett egy figurát a százszög egyik csúcsán. Ezután mindennap a figurát annyi csúccsal helyezte arrébb az óramutató járása szerint haladva, amennyi annak a csúcsnak az indexe, amelyen a figura állt (A_3-ról az A_6-ra teszi, A_{96}-ról az A_{92}-re). Most (2013. április 12.) a figura az A_{100}-on áll. Mennyi volt a valószínűsége annak, hogy ez történik?
0.04=\frac1{25}
23 J / 13 S
Egy pozitív egészet különös-nek nevezünk, ha felírható két egész négyzetének a különbségeként. Hány különös számot találunk az 1,2, \dots, 2013 számok között?
1510
24 J / 14 S
Van három egységoldalú, egymást nem fedő szabályos konvex sokszögünk, amelyeknek van egy A közös pontja. Ezen sokszögek uniója egy M konkáv sokszög, amelynek az A belső pontja. Ha az egyik sokszög egy négyzet, a másik pedig egy hatszög, akkor mekkora M kerülete?
16
25 J / 15 S
Matyi felírta 1-től 100-ig az egész számokat véletlenszerű sorrendben. Mennyi a valószínűsége, hogy minden i-re, ahol i = 1,\dots,50 a 2i-1-edik helyen lévő szám kisebb, mint a 2i-edik helyen lévő szám?
2^{-50}
26 J / 16 S
A pink festéket piros és fehér festékből keverik 1:1 arányban, a cián festéket pedig kék és fehér festékből 1:2 arányban. Angi olyan festékkel szeretné kifesteni a szobáját, amit pink és cián festékből kever 2:1 arányban. Már összekevert 3 doboz kék és 1 doboz piros festéket. Hány doboz festéket kell még felhasználnia, ha már csak piros és fehér festék áll rendelkezésére?
23
27 J / 17 S
Van egy kalapunk, amiben fehér, szürke és fekete nyuszik vannak. Amikor a bűvész elkezdi véletlenszerűen kihúzni a nyuszikat a kalapból (visszatevés nélkül), annak a valószínűsége, hogy előbb húz ki egy fehéret, mint egy szürkét \frac34. Annak a valószínűsége, hogy előbb húz ki egy szürkét, mint egy feketét, szintén \frac34. Mennyi a valószínűsége annak, hogy előbb húz ki egy fehéret, mint egy feketét?
\frac{9}{10}
28 J / 18 S
Az a, b pozitív egészekre igaz, hogy 49a+99b = 2013. Mennyi a+b értéke?
37
29 J / 19 S
Egy 6\,\text{cm} oldalú PQRS négyzet sarkaiban elhelyezünk egy-egy kisebb, 2\,\text{cm} oldalú négyzetet. Jelöljük a négyzetek PQRS belsejében lévő csúcsait W, X, Y, Z betűkkel, ahogy az ábrán látható. Ezután szerkesztünk egy ABCD négyzetet olyan módon, hogy a W, X, Y, Z csúcsok rendre rajta vannak az AB, BC, CD, DA oldalakon. Legfeljebb mekkora lehet a P és D pontok közötti távolság?
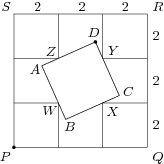
6
30 J / 20 S
Van 20 dobozunk, amelyekben összesen 129 alma van. Tudjuk, hogy néhány dobozban pontosan 4 alma van, míg a többi dobozban pontosan x alma van. Melyek x lehetséges értékei?
11, 53
31 J / 21 S
a és b olyan valós számok, hogy a > b > 0 és Mennyi az \frac{a+b}{a-b} kifejezés értéke?
\sqrt{\frac{2015}{2011}}
32 J / 22 S
Hányféleképpen írhatjuk be az egész számokat 1-től 7-ig az ábrán látható négyzetekbe úgy, hogy minden számot csak egyszer használhatunk fel, és az alsó sorban lévő számok összege megegyezik a bal oldali oszlopban lévő számok összegével?
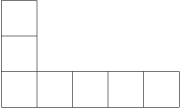
144=3 \cdot 2 \cdot 4!
33 J / 23 S
Legyen ABC egy hegyesszögű háromszög, ahol AB=4\pi, BC=4\pi+3, CA=4\pi+6. Jelöljük az A-hoz tartozó magasság talppontját D-vel. Mennyi CD-BD?
12
34 J / 24 S
Piripócson a villamosok mindennap mindkét irányban ugyanolyan időközönként közlekednek. Pumukli a villamossínek mentén sétálva azt tapasztalta, hogy 12 percenként előzte meg a villamos, és 4 percenként haladt el mellette a másik irányból jövő villamos. Milyen időközönként járnak Piripócson a villamosok?
6 minutes
35 J / 25 S
Hányféleképpen választható ki három pont az ábrán látható pontok közül úgy, hogy a három pont ne essen egy egyenesbe?
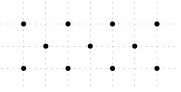
Note: Points are aligned in the indicated grid.
148=\binom{11}{3}-17
36 J / 26 S
Tominak van egy doboz csokija, amiben 30 darab csoki van három 10-es sorban. Olyan módon fogyasztja el egyenként a csokikat, hogy bármely két sorban a csokik száma közötti különbség legfeljebb 1 legyen. Hányféleképpen eheti meg az egész doboz csokit?
6^{10}\cdot (10!)^3
37 J / 27 S
Egy hatjegyű pozitív egész számot duplázó-nak hívunk, ha az első három számjegyből álló szám megegyezik az utolsó három számjegyből álló számmal. Például 227227 duplázó, de 135153 nem az. Hány duplázó szám osztható 2013-mal?
Megjegyzés: Egy pozitív egész szám első számjegye nem lehet 0.
5
38 J / 28 S
Tegyük fel, hogy van egy 4\times 4-es sakktáblánk, amin minden négyzetbe egy lefele vagy jobbra mutató nyilat rajzolunk véletlenszerűen. Ezután elindulunk a bal felső sarokból, és a nyilak irányának megfelelően haladunk, amíg ki nem lépünk a sakktábláról. Mennyi a valószínűsége, hogy a jobb alsó sarokból lépünk ki a sakktábláról?
\frac{5}{16}=\frac{\binom{6}{3}}{2^6}
39 J / 29 S
Hozzuk a törtet a lehető legegyszerűbb alakra (azaz olyan \frac{a}{b} alakra, ahol a és b relatív prímek).
\frac{70}{37}
40 J / 30 S
Van egy ABCD téglalapunk, ahol AB=30 és BC=20. Az AB oldal hány X pontjára lesz a CDX háromszög kerülete egész szám?
13
41 J / 31 S
Milyen sorrendbe rakjuk az ábrán látható táblázat r_1, \dots, r_{11} sorait, hogy az így kapott táblázat szimmetrikus legyen a megjelölt átlóra? Elegendő egy megoldást találni.

visszafelé (vagy ebben a sorrendben a sorokat ciklikusan eltologatva), például r_{11},r_{10},r_9,\dots,r_1 or r_{10},r_9,\dots,r_1,r_{11}, …, r_1,r_{11},r_{10},\dots, r_2
42 J / 32 S
Minden pozitív egész n-re legyen Melyik az a legkisebb k\geq 2 egész, amire a_2\cdot a_3 \cdots a_k>4?
254
43 J / 33 S
Barbi n egyenlő szeletre vágta fel a pizzát, majd megjelölte a szeleteket az 1,2,\dots,n számokkal (minden számot pontosan egyszer használt fel). Úgy számozta meg őket, hogy bármely két szomszédos egészekkel (i és i+1) jelölt szelet között pontosan k másik szelet van. Aztán jött Pocakos Peti, és megette majdnem az egész pizzát, csak három egymás melletti szeletet hagyott, a 11, 4, 17 számokkal jelölteket, ebben a sorrendben. Hány szelet pizza volt eredetileg?
20
44 J / 34 S
Az ELTE egyik előadótermében a székek úgy vannak elhelyezve, hogy egy téglalap alakú rácsot alkotnak. Az egyik előadás alatt pontosan 11 fiú ült mindegyik sorban, és pontosan 3 lány mindegyik oszlopban, emellett 2 szék üres volt. Legalább hány szék van az előadóban?
144
45 J / 35 S
A 3 egység sugarú k kör belülről érinti a 4 egység sugarú l kört a T pontban. Legfeljebb mekkora lehet a TKL háromszög területe, ha K \in k és L \in l.
9\sqrt3= \frac{27}{\sqrt{3}}
46 J / 36 S
Eszti és Feri a következő játékot játssza: A kezdésnél vesznek egy számhalmazt: Ebből először Eszti elhagy 2^9 elemet, majd Feri 2^8 elemet, majd Eszti 2^7 elemet, és így tovább, végül Feri elhagy egy elemet, így pontosan két szám marad. A játék ekkor véget ér, és Eszti kifizeti Ferinek forintban a két megmaradó szám különbségének az abszolútértékét. Hány forintot kap Feri, ha a lehető legjobban játszanak mindketten?
32
47 J / 37 S
Néhány ELTE-s diák megbukott a vizsgákon, és kirúgták őket, ezért elmentek tanulni a Másik Egyetemre. Ez a következő következményekkel járt:
- Az ELTE-s diákok száma egyhatoddal csökkent.
- A Másik Egyetem diákjainak száma egyharmaddal nőtt.
- Az átlag IQ mindkét egyetemen 2%-kal emelkedett.
Hányszorosa az ELTE-sek átlag IQ-ja a Másik Egyetemen tanuló diákok átlag IQ-jának?
\frac65 = 1.2-times
48 J / 38 S
Egy A_1A_2\dots A_{14} szabályos 14-szöget beírunk egy egységsugarú k körbe. A k által határolt körlapból mekkora területet fog közre a \angle A_1A_4A_{14} szög?
\frac{\pi}{14}
49 J / 39 S
Jancsi és Juliska vették a következő 24 elemű halmazt: \{1, 2, \ldots, 24\}. Jancsi felírta azokat a 12 elemű részhalmazokat, amelyekben páros az elemek összege, míg Juliska azokat a 12 elemű részhalmazokat írta fel, amelyekben páratlan az elemek összege. Ki írt fel több részhalmazt,és mennyivel?
Jancsi, \binom{12}6 = 924-gyel többet
50 J / 40 S
Géza három különböző a, b, c pozitív egészre gondolt, amelyek közül valamely kettőnek az összege 800. Ezután leírta az a, b, c, a+b-c, a+c-b, b+c-a és a+b+c kifejezéseket egy papírra, és azt vette észre, hogy mind prímek. Határozzuk meg a papírra leírt legnagyobb és legkisebb szám különbségét.
1594
51 J / 41 S
Ági megjelölt egy-egy folttal két véletlenszerűen kiválasztott helyet egy méterrúdon, Ezután jött Balázs, és széttörte a méterrudat véletlenszerűen 2013 darabra. Mennyi a valószínűsége, hogy a két kijelölt hely ugyanazon a darabon van?
\frac1{1007}
52 J / 42 S
Hány olyan tízjegyű pozitív egész szám van, amiben a 0,1,\dots ,9 számjegyek mindegyike pontosan egyszer szerepel, és 11 111-nek többszöröse?
Megjegyzés: Egy pozitív egész szám első számjegye nem lehet 0.
3456 = 2^5\cdot 5! - 2^4\cdot 4!
53 J / 43 S
Egy 2013-adfokú valós együtthatós P(x) polinom n=0,1,\dots,2013-ra kielégíti a P(n)=3^n egyenletet. Mennyi P(2014) értéke?
3^{2014}-2^{2014}
54 J / 44 S
Egy egyenlő szárú ABC háromszögben AB=AC és \angle BAC=99.4^\circ, és adott a D pont, amelyre AD=DB és \angle BAD=19.7^\circ. Számítsd ki, mekkora \angle BDC.
149.1^\circ
55 J / 45 S
Melyik a legnagyobb nem nullára végződő pozitív egész, amelynek valamely “belső” számjegyét elhagyva a szám egy osztóját kapjuk?
Megjegyzés: A “belső” számjegy olyan számjegy a számban, ami nem az első vagy az utolsó számjegy.
180625
56 J / 46 S
Adottak a, b, c páronként különböző valós számok, melyekre Mennyi az abc szorzat értéke?
3
57 J / 47 S
Egy általános ABC háromszögben az egyik magasság hossza megegyezik az egyik súlyvonal hosszával, illetve egy másik magasság hossza is megegyezik egy másik súlyvonal hosszával. Mekkora a harmadik magasság, és a harmadik súlyvonal hosszának aránya?
\frac{2}{7}