1 J
Zlatá cihlička je kvádr o rozměrech 2\times 3\times 4. Cihlička byla roztavena a ze všeho získaného zlata byly zhotoveny tři stejné krychle. Zjistěte délku hrany každé z nich.
2
2 J
Novoročních oslav v restauraci U Vybitého zásobníku se zúčastnilo 43 lidí. Na baru se podával džus, pivo a šampaňské. Pivo pilo 25 lidí a šampaňské pilo 19 lidí, přičemž pivo a šampaňské dohromady pilo 12 lidí. Všichni ostatní ten večer řídili, takže pili jen džus. Kolik lidí pilo pouze džus?
11
3 J
Vypitím jednoho šálku černého čaje získáme kofein na jednu hodinu. Vypitím jednoho šálku kávy získáme kofein na čtyři hodiny. V jakém poměru je třeba smíchat černý čaj a kávu, abychom v jednom šálku získali kofein na dvě hodiny?
2:1
4 J
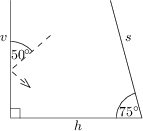
Zrcadla v a h na obrázku jsou navzájem kolmá a úhel mezi zrcadly h a s má velikost 75^\circ. Paprsek dopadl na v pod úhlem 50^\circ a pokračoval odrazem od h a následně od s. Pod jakým úhlem poté dopadne znovu na v?
Poznámka: Úhlem odrazu/dopadu zde rozumíme odchylku dopadajícího paprsku od zrcadla. Paprsek se odráží pod stejně velkým úhlem, pod jakým dopadá.
80
5 J
V zakázkami nabitém roce 2013 se v obchodě prodalo 235 kusů nábytku, přičemž v každém měsíci to bylo buď 20, nebo 16, nebo 25 kusů. V kolika měsících se prodalo 20, v kolika 16 a v kolika 25 kusů nábytku?
4, 5, 3
6 J
Dvě kružnice mají poloměry 5 a 26. Menší z nich prochází středem větší. Uvažme nejkratší a nejdelší tětivu větší kružnice, které se obě dotýkají menší kružnice. Jaký je rozdíl jejich délek?
4
7 J
Leoš Mareš se narodil v minulém století. Víme, že v roce 1999 byl jeho věk roven součtu cifer v čísle roku jeho narození. Ve kterém roce se narodil?
1976
8 J
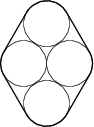
David si vyrobil tankový pás jako na obrázku. Všechna kola kromě vrchního a spodního se navzájem dotýkají. Jaká je délka pásu, víme-li, že kola mají poloměr 1 a pás je kolem nich těsně natažen?
8+2\pi
9 J
Broučci se na tělocviku řadí podle počtu nohou. Kromě Pytlíka dnes dorazili ještě čtyři broučci s počty nohou 6, 3, 10 a 9. Víme, že po seřazení byl počet nohou broučka uprostřed roven aritmetickému průměru počtu nohou všech přítomných broučků. Kolik nohou měl Pytlík? Najděte všechny možnosti.
2, 7, 17
10 J
Pro nenulové číslice A, B, C platí \overline{AA} + \overline{BB} + \overline{CC} = \overline{ABC}. Určete \overline{ABC}.
Poznámka: Zápisem \overline{XY} pro číslice X, Y rozumíme číslo, jehož desítkový zápis je XY.
198
11 J / 1 S
Vášnivý sběratel hudebních nástrojů Pepa byl v důsledku ekonomické krize nucen prodat třetinu své sbírky. Hned potom daroval Alče tři flétny od Hieronyma Bosche. Později znovu prodal třetinu z toho, co mu zbylo, a věnoval Davidovi dvoje stradivárky a dvě gibsonky. Když naposled prodal třetinu zbylých nástrojů a tři daroval muzeu, zbylo mu v domácí galerii už jenom devět klavírů, se kterými nemohl hnout. Kolik nástrojů měl na začátku?
54
12 J / 2 S
Najděte nejmenší přirozené číslo větší než 2014, které se nedá zapsat jako součet dvou palindromů.
Poznámka: Palindrom je číslo, jehož desítkový zápis se čte stejně odpředu jako odzadu.
2019
13 J / 3 S
Štěpán dal Lukášovi hádanku. Vybral si číslici X a řekl: „Myslím si trojciferné číslo dělitelné jedenácti. Na pozici stovek má číslici X a na pozici desítek trojku. Tvým úkolem je zjistit číslici na pozici jednotek.“ Lukáš se na chvilku a zamyslel a vykřikl: „Ha, už vím, jak na to!“ Ale pak si uvědomil, že hádanka nemá řešení – žádná číslice na pozici jednotek nevyhovuje popsaným vlastnostem Štěpánova čísla. Jakou číslici Štěpán za X vybral?
4
14 J / 4 S
David si vymyslel čísla a<b<c<d a spočítal součty každých dvou z nich (celkem šest součtů). Zjistil, že každý součet je jiný a že čtyři nejmenší součty jsou 1, 2, 3 a 4. Jakou hodnotu může mít d? Najděte všechny možnosti.
3{,}5; 4
15 J / 5 S
Říká takhle Křemílek Vochomůrkovi: „Je mi dvakrát více let, než bylo tobě, když jsem byl tak starý, jako jsi ty dnes. Až budeš starý jako já, bude nám dohromady 90 let.“ Kolik let je Křemílkovi?
40
16 J / 6 S
Kladná celá čísla a_1,a_2,a_3,\ldots tvoří aritmetickou posloupnost. Pokud a_1 = 10 a a_{a_2} = 100, čemu je rovno a_{a_{a_3}}?
820
17 J / 7 S
Alčino oblíbené číslo má následující vlastnosti:
- Má celkem osm cifer.
- Jeho cifry jsou navzájem různé a zleva doprava se zmenšují.
- Je dělitelné 180.
Jaké je to číslo?
97654320
18 J / 8 S
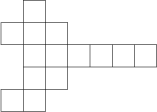
Kikina si ráda skládá trojrozměrná tělesa ze čtverečkovaného papíru. Naposledy si vystřihla útvar jako na obrázku a slepila ho tak, že se žádné dva čtverečky nepřekrývaly a výsledné těleso nemělo díry a mělo nenulový objem. Jaký byl počet vrcholů tohoto tělesa? Poznámka: Mřížové body pláště uvnitř hran tělesa se za vrcholy nepočítají.
12
19 J / 9 S
Pro přirozená čísla a, b platí ab = \nsn(a,b) + \NSD(a,b). Najděte všechny takové dvojice (a,b).
Poznámka: Symbolem \nsn(a,b) rozumíme nejmenší společný násobek čísel a, b a symbolem \NSD(a,b) jejich největší společný dělitel.
(2,2)
20 J / 10 S
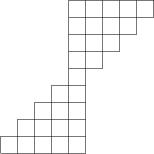
Žába skáče na hřišti složeném z 29 políček, které je vyobrazeno na přiloženém plánku. Začíná na libovolném políčku ve spodním řádku a v každém kroku může skočit o jedno políčko nahoru nebo šikmo doprava nahoru (pokud tam nějaké je). Žába skáče, dokud se neocitne v horním řádku. Kolik různých cest může proskákat?
256
21 J / 11 S
Při své honbě za truhlicemi nabitými poklady stál jednoho dne Olin před úkolem projít bludiště. Mělo tvar pravidelného osmiúhelníku a cesty vedly po jeho úhlopříčkách. Olin začal v pevně daném vrcholu a měl projít bludiště tak, aby každou úhlopříčku navštívil právě jednou. Kolika způsoby to mohl provést?
0
22 J / 12 S
Máme tabulku T o rozměrech 2014 \times 2014 s levým dolním rohem v bodě [0,0] a pravým horním v bodě [2014,2014]. Přímka p prochází body o souřadnicích [0, 0] a [2014, 2019]. Kolik políček tabulky T přímka p protíná?
Poznámka: Přímka p protíná políčko tabulky, pokud s ním má společné alespoň dva body. Například diagonála protíná 2014 políček T.
4023
23 J / 13 S
Konvexní mnohoúhelník má všechny vnitřní úhly až na jeden rovny 150^\circ, zbývající úhel může mít libovolnou velikost. Najděte všechny možné počty vrcholů takového mnohoúhelníka.
8, 9, 10, 11, 12
24 J / 14 S
Délky stran trojúhelníka splňují vztah Jaký úhel svírají strany b a c?
60^{\circ}
25 J / 15 S
Najděte všechna celá čísla mezi 1 a 200 včetně taková, že součet všech jejich prvočíselných dělitelů je 16. Každé prvočíslo přitom počítáme pouze jednou, tedy například součet různých prvočíselných dělitelů čísla 12 je 2+3=5.
66, 132, 198, 55, 39, 117
26 J / 16 S
Pro vzdálenosti bodů na obrázku platí, že |DA| = |AB| = |BE|, |GA| = |AC| = |CF| a |IC| = |CB| = |BH|. Jaký je obsah trojúhelníka ABC, když navíc |EF| = 5, |DI| = 5 a |GH| = 6?
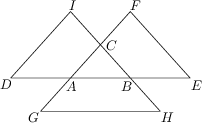
3
27 J / 17 S
Prvočíslo p nazveme mocné, jestliže:
- p je jednociferné, nebo
- po odebrání jeho první cifry dostaneme opět mocné prvočíslo a totéž platí pro poslední cifru.
Například 37 je mocné prvočíslo, jelikož odebráním první cifry vznikne 7 a odebráním poslední cifry vznikne 3, což jsou obě mocná prvočísla. Najděte všechna mocná prvočísla.
2, 3, 5, 7, 23, 37, 53, 73, 373
28 J / 18 S
Jsou dány dvě kružnice k, l o poloměru 16, z nichž každá prochází středem té druhé. Sestrojme kružnici m tak, aby měla vnitřní dotyk s k i s l, a navíc se dotýkala spojnice jejich středů. Jaký je poloměr m?
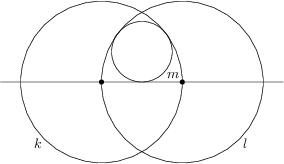
6
29 J / 19 S
V kolika šesticiferných číslech se každá cifra vyskytuje tolikrát, jaká je její hodnota? Číslem s těmito vlastnostmi je například 133232.
82
30 J / 20 S
E.T. si jako správný chlap slepil 4 koule o poloměru 1 tak, aby se všechny navzájem dotýkaly. Jaký je poloměr nejmenší koule, do níž se všechny E.T.-ho koule vejdou?
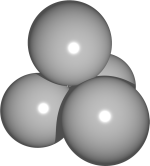
1+\frac{\sqrt{6}}2 = \frac{\sqrt{6}+2}{2}
31 J / 21 S
Pro přirozená čísla x, y platí 100\geq x>y. Čísla x^2 - y^2 a x^3 - y^3 jsou přitom nesoudělná. Kolik takových dvojic (x,y) existuje?
99
32 J / 22 S
Mějme číslo, které začíná 122333444455555\dots a pokračuje tak, že každé další přirozené číslo napíšeme za sebou tolikrát, jaká je jeho hodnota. Po napsání 2014 cifer skončíme. Jaká je poslední napsaná cifra?
4
33 J / 23 S
Najděte nejmenší přirozené číslo N, pro které má rovnice (x^2-1)(y^2-1)=N alespoň dvě různá řešení x,y \in \mathbb{N}, x\leq y.
360
34 J / 24 S
Dvě kružnice s poloměry 1 a 3 mají v bodě A vnější dotyk. Jejich společná tečna neprocházející bodem A se jich dotýká postupně v bodech B a C. Čemu se rovná |AB|^2+|BC|^2+|AC|^2?
24
35 J / 25 S
Najděte největší prvočíslo p splňující p^p \mid 2014!.
Poznámka: Symbol „!“ označuje faktoriál, který je definován jako n! = 1 \cdot 2 \cdots n.
43
36 J / 26 S
Mějme tabulku 2 \times 2014. Kolika způsoby je možné ji obarvit třemi barvami tak, aby žádná dvě políčka sdílející hranu neměla stejnou barvu?
6 \cdot 3^{2013}
37 J / 27 S
Najděte nejmenší přirozené číslo m takové, že 5m je pátá mocnina celého čísla, 6m je šestá mocnina celého čísla a 7m je sedmá mocnina celého čísla.
5^{84}6^{35}7^{90}
38 J / 28 S
Máme obdélníkový list papíru. Když jej přeložíme tak, aby se dva protilehlé rohy dotýkaly, vznikne nám přehyb stejné délky, jako je delší strana papíru. Jaký je poměr delší strany ku kratší straně původního obdélníku?
\sqrt{\frac{1 + \sqrt{5}}{2}}
39 J / 29 S
Máme 20 barevných kuliček, z nichž každá je modrá, žlutá, zelená, nebo červená. Kolik nejvíce může být modrých kuliček, jestliže počet všech barevně různých posloupností délky 20, jež se dají z kuliček poskládat, je přesně 1140?
17
40 J / 30 S
Najděte všechna možná n \geq 3, pro která lze pravidelný n-úhelník rozdělit na několik (aspoň dva) pravidelných mnohoúhelníků.
3, 4, 6, 12
41 J / 31 S
V levém dolním rohu šachovnice 5\times 5 se nachází šachová věž. V každém tahu se tato věž přesune o libovolný nenulový počet políček doprava, nebo nahoru. Kolika způsoby se může dostat do pravého horního políčka?
Poznámka: Dva způsoby projití považujeme za shodné, pouze pokud se přesně shodují všechny tahy v pořadí jejich provedení.
838
42 J / 32 S
Jaká číslice se nachází na pozici stovek čísla 11^{2014}?
2
43 J / 33 S
Kobylka skáče po vrcholech rovnostranného trojúhelníka. Vždy, když stojí v některém vrcholu, si jako cíl dalšího skoku náhodně vybere jeden ze dvou zbylých vrcholů. Jaká je pravděpodobnost, že po deseti skocích skončí v tom vrcholu, ve kterém začínala?
\frac{171}{512}
44 J / 34 S
Lukáš jde kácet stromy, na začátku má 100 jednotek síly. Každou minutu se může rozhodnout mezi dvěma možnostmi:
- Vykácí n stromů, kde n je jeho současná síla. To ho unaví, takže se jeho síla následně sníží o 1.
- Odpočine si a získá 1 jednotku síly.
Kolik nejvíce stromů může Lukáš vykácet během šedesáti minut?
4293
45 J / 35 S
Nechť \sqrt{\mathbb{N}} = \bigl\{\sqrt{1},\sqrt{2},\sqrt{3},\sqrt{4}, \dots \bigr\} je množina odmocnin přirozených čísel. Nechť S je množina čísel a \in \sqrt{\mathbb{N}} takových, že současně \frac{36}{a} \in \sqrt{\mathbb{N}}. Jaký je součin prvků množiny S?
6^{25}
46 J / 36 S
Šavlík vybral 2014 náhodných celých čísel od nuly do devíti a navzájem je vynásobil. S jakou pravděpodobností dostal číslo dělitelné deseti?
1-\bigl(\frac{5}{10}\bigr)^{2014} - \bigl(\frac{8}{10}\bigr)^{2014} + \bigl(\frac{4}{10}\bigr)^{2014}
47 J / 37 S
Určete hodnotu výrazu: Poznámka: Symbol \lfloor x \rfloor označuje dolní celou část x, tedy největší celé číslo nepřevyšující x.
-2002
48 J / 38 S
Martin počítal součet 1+2+\dots+2012. Zapomněl ale přičíst některá čísla, a tak dostal výsledek dělitelný 2011. Anička počítala součet A=1+2+\dots+2013, přičemž zapomněla přičíst ta samá čísla jako Martin, a tak dostala tak součet N dělitelný 2014. Určete poměr \frac{N}{A}.
\frac23
49 J / 39 S
Vejtek má novou hru. Hraje se s šestnácti kartami, které jsou položené v řadě za sebou. Každá karta je z jedné strany červená a z druhé černá. V každém tahu najde Vejtek tu černou kartu, která je nejvíce vpravo. Tuto kartu otočí a společně s ní otočí i všechny karty, které jsou od ní napravo. Hra skončí, jakmile už není možné táhnout. Kolik nejvýše tahů může Vejtek provést?
2^{16} - 1
50 J / 40 S
Kolik existuje pravoúhlých trojúhelníků s celočíselnými délkami stran takových, že alespoň jedna jejich odvěsna má délku 2014^{14}?
\frac12(27 \cdot 29^2 - 1)=45\,412
51 J / 41 S
Jaké je nejmenší přirozené číslo, které se nedá zapsat jako součet jedenácti nebo méně (ne nutně různých) faktoriálů? Například: 42 = 4! + 3! + 3! + 2! + 2! + 1! + 1!.
359
52 J / 42 S
Na šachovém turnaji hraje každý s každým. Navíc se hráči dohodli, že partie nemůže skončit remízou. Skupinu šachistů nazveme jasnou, pokud je v ní hráč, který porazil všechny ostatní členy skupiny, a hráč, který byl všemi ostatními členy skupiny poražen. Najděte nejmenší n takové, že v každém turnaji n šachistů už musí nutně existovat jasná skupina čtyř hráčů.
8
53 J / 43 S
Dáška si vymyslela dvě celá čísla od jedné do devíti. Davidovi prozradila jejich součin a Pepovi jejich součet. Následoval takovýto rozhovor:
- David: „Nevím, jaká jsou ta čísla.“
- Pepa: „Nevím, jaká jsou ta čísla.“
- David: „Nevím, jaká jsou ta čísla.“
- Pepa: „Nevím, jaká jsou ta čísla.“
- David: „Nevím, jaká jsou ta čísla.“
- Pepa: „Nevím, jaká jsou ta čísla.“
- David: „Nevím, jaká jsou ta čísla.“
- Pepa: „Nevím, jaká jsou ta čísla.“
- David: „Už vím, jaká jsou ta čísla!“
Jaká čísla si Dáška vymyslela?
2, 8
54 J / 44 S
Mezi tři stejné kužely, které stojí na podložce tak, že se navzájem dotýkají podstavami, jsme vložili kouli. Koule je tak velká, že její nejvyšší bod leží ve stejné výšce jako vrcholy kuželů. Kužely mají podstavu o poloměru 50 cm a jejich výška je 120 cm. Zjistěte poloměr koule.

\frac{200\sqrt{3}}{9}
55 J / 45 S
Řádky a sloupce tabulky 7 \times 7 jsou standardně očíslovány čísly 1, 2, \ldots , 7. Kolika způsoby můžeme do políček tabulky rozmístit osm nábojnic tak, že pro každé dvě nábojnice bude rozdíl čísel jejich řádků nebo rozdíl čísel jejich sloupců alespoň tři?
51
56 J / 46 S
Jsou dány tři body A, B a C, které neleží v přímce. Úsečka AB je dělícími body D a E rozdělena na tři stejně dlouhé části. Bod F je středem úsečky AC. Přímky EF a BF protínají přímku CD v bodech G a H (v tomto pořadí). Je-li obsah trojúhelníka DEG roven 18, jaký je obsah trojúhelníka FGH?
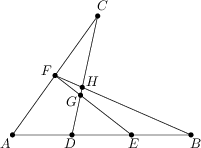
1{,}8
57 J / 47 S
Plášť tělesa je tvořen dvěma rovnostrannými trojúhelníky s délkou strany 1 a šesti rovnoramennými trojúhelníky s rameny délky x a podstavou délky 1, viz obrázek. Je-li objem tělesa 6, čemu je rovno x?
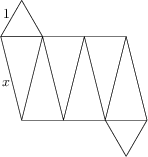
\frac{5\sqrt{39}}{3}






















