1 J
Peter ist gelernter Goldschmied. Seinen Goldbarren der Größe 2\times 3\times 4 hat er eingeschmolzen und aus dem entstandenen flüssigen Gold drei gleich große Würfel gegossen.
Wie lang sind die Kanten dieser Würfel?
2
2 J
Auf einer Silvesterparty trafen sich 43 Personen. An der Bar wurden Saft, Bier und Champagner ausgeschenkt. Während der Feier konsumierten 25 Personen Bier, 19 Personen tranken Champagner und 12 Personen kauften sich sowohl Bier als auch Champagner. Die übrigen Personen waren als Fahrer eingeteilt, weshalb sie nur Saft tranken.
Wie viele Personen tranken nur Saft?
11
3 J
Wenn man eine Tasse Kaffee trinkt, nimmt man Koffein für 1 Stunde auf. Wenn man eine genauso große Tasse Espresso trinkt, führt man seinem Körper Koffein für 4 Stunden zu.
In welchem Verhältnis muss man Kaffee mit Espresso mischen, um in einer Tasse das Koffein für genau 2 Stunden zu haben?
2:1
4 J
Drei Spiegel v, h und s sind wie in nachfolgender Skizze angeordnet, wobei die Spiegel v und h senkrecht aufeinander stehen. Der Winkel zwischen den Spiegeln s und h beträgt 75^\circ.
Ein Lichtstrahl fällt unter dem Winkel 50^\circ auf den Spiegel v, wird reflektiert, trifft dann auf den Spiegel h und wird dort reflektiert, trifft auf den Spiegel s, wird reflektiert und trifft schließlich wieder auf den Spiegel v.
Unter welchem Einfallswinkel trifft der Lichtstrahl das letzte Mal auf den Spiegel v?
Hinweis: Bei der Reflexion eines Lichtstrahls an einem Spiegel ist der Einfallswinkel des Strahls genau so groß wie der Ausfallswinkel des Strahls.
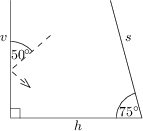
80^\circ
5 J
Im Jahr 2013 verkaufte ein Spielwarengeschäft insgesamt 235 Lokomotiven für Modelleisenbahnen. In jedem Monat gingen entweder 20,\ 16 oder 25 Stück über den Ladentisch.
Finde heraus, in wie vielen Monaten genau 20, in wie vielen Monaten genau 16 und in wie vielen genau 25 Lokomotiven verkauft wurden.
4,\ 5,\ 3
6 J
Gegeben seien zwei Kreise mit den Radien 5 bzw. 26, wobei der Mittelpunkt des größeren Kreises auf der Kreislinie des kleineren Kreises liegen soll. Man betrachtet nun alle Sehnen im großen Kreis, welche den kleinen Kreis berühren. Von diesen gibt es eine längste und eine kürzeste Sehne.
Was ist die Differenz der Längen dieser beiden extremalen Sehnen?
4
7 J
Meine Cousine Agnes wurde im letzten Jahrhundert in München geboren. Ihr Alter im Jahr 1999 war gleich der Quersumme ihres Geburtsjahres.
In welchem Jahr wurde Agnes geboren?
1976
8 J
Vier Keise mit Radius 1 berühren sich gegenseitig wie in der Abbildung dargestellt. Um diese Kreise wird, wie eingezeichnet, ein Gummiband gespannt.
Wie lang ist dieses Band?
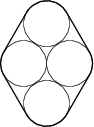
8+2\pi
9 J
In die Käferschule gehen alle erdenklichen Arten von Käfern mit den unterschiedlichsten Anzahlen an Beinen. Der dortige Sportlehrer ordnet seine Schüler (Käfer) immer in einer Reihe an, beginnend von der kleinsten Beineanzahl hin zur größten.
In der letzten Sportstunde waren nur fünf Schüler anwesend: Käfer Buggy und noch vier weitere Käfer, die 6,\ 3,\ 10 und 9 Beine hatten. Sie stellten sich in einer Reihe auf, so wie ihr Lehrer das möchte, und bemerkten erstaunt, dass dann der mittlere Käfer genau so viele Beine hatte wie das arithmetische Mittel der Beine aller fünf Käfer!
Bestimme alle möglichen Beineanzahlen für Buggy.
2,\ 7,\ 17
10 J
Die von Null verschiedenen Ziffern A, B und C erfüllen das Kryptogramm Bestimme die Lösungszahl ABC.
198
11 J / 1 S
Zaphod, ein berühmter Sammler von Himmelskörpern, musste aufgrund von finanziellen Schwierigkeiten ein Drittel seiner Sammlung verkaufen. Anschließend schenkte er seiner Tochter drei Planeten des Sonnensystems. Später veräußerte er ein Drittel der verbliebenen Himmelskörper seiner Sammlung und vermachte seiner Frau zwei Jupitermonde sowie zwei Monde des Saturn. Als er sich erneut gezwungen sah, weitere Teile seiner Sammlung zu Geld zu machen, verkaufte er abermals ein Drittel seiner Himmelskörper, die er noch besaß, und schenkte seinem Sohn den Mars und dessen zwei Monde. Schließlich waren in seiner Sammlung nur noch neun Planeten aus Alpha Centauri übrig.
Wie viele Himmelskörper besaß Zaphod zu Beginn?
54
12 J / 2 S
Bestimme die kleinste Zahl, die größer als 2014 ist und nicht als Summe zweier Palindrome geschrieben werden kann.
Hinweis: Palindrome sind natürliche Zahlen, deren Darstellung von links sowie von rechts gelesen den gleichen Wert hat. Beispielsweise ist 7447 ein Palindrom.
2019
13 J / 3 S
Florian gab Hannes ein Zahlenrätsel auf. Er teilte ihm eine Ziffer mit und sagte:
„Ich denke mir eine dreistellige Zahl, die durch 11 teilbar ist. Die Ziffer an der Hunderterstelle ist meine gewählte Ziffer X und die Ziffer an der Zehnerstelle ist eine 3. Finde nun die Ziffer an der Einerstelle.“
Hannes erkannte schnell, dass er verschaukelt wurde, da es gar keine solche Ziffer für die Einerstelle geben kann!
Welche Ziffer X hatte Florian seinem Freund Hannes mitgeteilt?
4
14 J / 4 S
Die vier rationalen Zahlen a < b < c < d können auf sechs Arten zu Paaren zusammengefasst werden.
Bestimme alle möglichen Werte für d im Fall, dass die sechs Paare unterschiedliche Summen haben und die vier kleinsten Summen 1,\ 2,\ 3 und 4 sind.
3.5,\ 4
15 J / 5 S
Sebastian ist zweimal so alt wie Tobias war, als Sebastian so alt war wie Tobias jetzt ist. Wenn Tobias so alt sein wird wie Sebastian jetzt ist, dann werden beide zusammen 90 Jahre alt sein.
Wie alt ist Sebastian?
40
16 J / 6 S
Gegeben sei eine arithmetische Folge a_1, a_2, a_3, \ldots positiver ganzer Zahlen mit dem Anfangswert a_1 = 10 und dem weiteren Wert a_{a_2} = 100.
Berechne das Folgenglied a_{a_{a_3}}.
820
17 J / 7 S
Julias Lieblingszahl besitzt jede der folgenden Eigenschaften:
- Sie besteht aus acht verschiedenen Ziffern.
- Die Ziffern sind fallend geordnet, wenn man sie von links nach rechts liest.
- Sie ist durch 180 teilbar.
Wie heißt die Lieblingszahl von Julia?
97654320
18 J / 8 S
Katharina bastelt gerne aus kariertem Papier Modelle von 3-dimensionalen Objekten. Das letzte Mal hat sie sich eine Form ausgeschnitten, wie sie in der unten stehenden Figur zu sehen ist. Sie hat das 2-dimensionale Netz an bestimmten Kanten gefaltet und diese so zusammengeklebt, dass sich keine zwei Quadrate überlappen und dass ein geschlossenes 3-dimensionales Objekt entsteht.
Wie viele Ecken hatte das gebastelte Objekt?
Hinweis: Gesucht sind die Ecken des 3-dimensionalen hergestellten Objekts, nicht die Ecken in der 2-dimensionalen Figur, die ausgeschnitten wird.
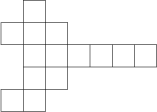
12
19 J / 9 S
Finde alle Paare positiver ganzer Zahlen a und b, für welche die Gleichung gilt.
Hinweis: Dabei bezeichnet \ggT(a,b) den größten gemeinsamen Teiler von a und b sowie \kgV(a,b) das kleinste gemeinsame Vielfache von a und b.
(2,\ 2)
20 J / 10 S
Im unten stehenden Diagramm sind 29 Einheitsquadrate angeordnet. Ein Frosch startet auf irgendeinem der fünf Einheitsquadrate der untersten Reihe und springt jede Sekunde entweder in das Quadrat direkt über seiner momentanen Position oder in das Quadrat diagonal nach rechts oben, vorausgesetzt natürlich, dass er von seinem Standpunkt aus ein solches Feld überhaupt erreichen kann. Das tut er, bis er auf einem Feld in der obersten Reihe angekommen ist.
Auf wie vielen verschiedenen Wegen kann der Frosch auf diese Weise von der untersten zur obersten Reihe gelangen?
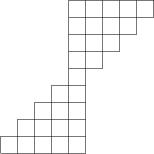
256
21 J / 11 S
Paul wandert auf den Diagonalen eines regelmäßigen Achtecks. Sein Weg beginnt an einer Ecke des Achtecks und soll über jede Diagonale genau einmal führen.
Wie viele verschiedene Wege kann Paul gehen?
0
22 J / 12 S
Gegeben sei ein Gitter aus Einheitsquadraten und darin ein Quadrat Q mit den Eckpunkten (0,0), (2014,0), (2014,2014) und (0,2014). Eine Diagonale von Q geht also durch das Innere von 2014 Einheitsquadraten. Die Gerade g gehe durch die Punkte (0,0) und (2014,2019).
Bestimme die Anzahl der Einheitsquadrate von Q, durch deren Inneres die Gerade g geht.
4023
23 J / 13 S
Ein konvexes n-Eck besitzt n-1 Winkel der Größe 150^\circ und einen Winkel beliebiger Größe.
Bestimme alle möglichen Werte, die n annehmen kann.
8,\ 9,\ 10,\ 11,\ 12
24 J / 14 S
Die Seiten a,\ b und c eines Dreiecks erfüllen die Gleichung Bestimme den Winkel zwischen den Seiten b und c.
60^\circ
25 J / 15 S
Bestimme alle natürlichen Zahlen n zwischen 1 und 200 mit der Eigenschaft, dass die Summe der unterschiedlichen Primfaktoren von n genau 16 ergibt.
Beispiel: Die Summe der unterschiedlichen Primfaktoren von 12 = 2^2\cdot 3 ist 2 + 3 = 5.
39,\ 55,\ 66,\ 117,\ 132,\ 198
26 J / 16 S
Die Streckenabschnitte in der gegebenen Zeichnung erfüllen die Gleichungen \overline{DA} = \overline{AB} = \overline{BE}, \overline{GA} = \overline{AC} = \overline{CF} und \overline{IC} = \overline{CB} = \overline{BH}. Außerdem sei \overline{EF} = 5,\ \overline{DI}=5 und \overline{GH} = 6.
Wie groß ist die Fläche des Dreiecks ABC?
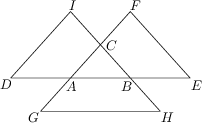
3
27 J / 17 S
Eine Primzahl p wird stark genannt, wenn sie eine der beiden folgenden Bedingungen erfüllt:
- p ist eine einstellige Primzahl oder
- sowohl durch das Entfernen der ersten Ziffer von p als auch durch das Entfernen der letzten Ziffer von p entsteht eine starke Primzahl.
Bestimme alle starken Primzahlen.
Beispiel: Die Zahl 37 ist eine starke Primzahl, da durch das Streichen der ersten Ziffer die Zahl 7 und durch das Streichen der letzten Ziffern die Zahl 3 entsteht, die beide selbst starke Primzahlen sind.
2,\ 3,\ 5,\ 7,\ 23,\ 37,\ 53,\ 73,\ 373
28 J / 18 S
Gegeben seien zwei Kreise k und l mit Radius 16, deren Mittelpunkte auf der jeweils anderen Kreislinie liegen. Ferner sei ein Kreis m gegeben, der die beiden Kreise k und l sowie die Verbindungsgerade der Mittelpunkte, wie in der Abbildung dargestellt, berührt.
Bestimme den Radius des Kreises m.
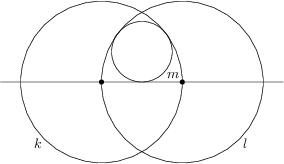
6
29 J / 19 S
Wie viele sechsstellige natürliche Zahlen gibt es, bei denen jede Ziffer so oft vorkommt wie ihr Wert angibt?
Beispiel: Die Zahl 133232 ist eine solche Zahl.
82
30 J / 20 S
Vier Kugeln mit Radius 1 berühren sich paarweise.
Bestimme den Radius der kleinsten Kugel, die alle vier Kugeln enthält.
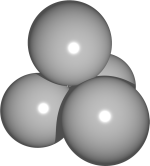
1+\frac{\sqrt 6}{2}
31 J / 21 S
Bestimme die Anzahl der Paare positiver ganzer Zahlen (x, y) mit y < x \leq 100, so dass x^2 - y^2 und x^3 - y^3 teilerfremd sind.
99
32 J / 22 S
Gegeben sei eine Zahl, die mit 122333444455555 \ldots beginnt und bei der in aufsteigender Reihenfolge jede Zahl so oft hintereinander geschrieben wird wie ihr Wert angibt. Nach 2014 Ziffern wird das Aufschreiben beendet.
Wie lautet die letzte Ziffer dieser Zahl?
4
33 J / 23 S
Bestimme die kleinste positive ganze Zahl n, für die die Gleichung (x^2 - 1)(y^2 - 1) = n mindestens zwei verschiedene Lösungen mit 0<x\leq y and x,\;y\in\mathbb{N} besitzt.
360
34 J / 24 S
Zwei Kreise mit den Radien 1 und 3 berühren sich gegenseitig im Punkt A und eine gemeinsame Tangente in den Punkten B und C.
Bestimme \overline{AB}^2+\overline{BC}^2+\overline{AC}^2.
24
35 J / 25 S
Bestimme die größte Primzahl p, welche die Bedingung p^p \mid 2014! erfüllt, wobei n! die Fakultät von n bezeichnet. Dabei ist die Fakultät von n durch n! = 1 \cdot 2 \cdots n definiert.
Beispiel: 5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 = 120.
43
36 J / 26 S
Gegeben sei eine Anordnung von Quadraten in zwei Spalten und 2014 Zeilen. Nun färbt man jedes Quadrat mit einer der Farben Rot, Grün und Blau so, dass zwei Quadrate mit einer gemeinsamen Seite unterschiedlich gefärbt sind.
Wie viele verschiedene solche Färbungen gibt es?
6\cdot3^{2013}
37 J / 27 S
Bestimme die kleinste positive ganze Zahl m mit der Eigenschaft, dass 5m eine fünfte Potenz, 6m eine sechste Potenz und 7m eine siebte Potenz ist.
5^{84}\cdot 6^{35}\cdot 7^{90}
38 J / 28 S
Gegeben sei ein rechteckiges Blatt Papier, das so gefaltet wird, dass zwei diagonal gegenüber liegende Ecken übereinander liegen. Dabei ist die Faltkante genau so lang wie die längere Rechtecksseite.
In welchem Verhältnis steht die längere zur kürzeren Rechtecksseite?
\sqrt{\frac{1+ \sqrt 5}{2}}
39 J / 29 S
Gegeben seien 20 Murmeln, jede in einer der Farben Weiß, Blau, Grün oder Rot. Dabei sollen Murmeln der gleichen Farbe nicht unterscheidbar sein.
Wie viele Murmeln können höchtens blau sein, wenn die Murmeln auf 1140 Möglichkeiten hintereinander auf einer Geraden angeordnet werden können?
17
40 J / 30 S
Bestimme alle natürlichen Zahlen n\ge 3 mit der Eigenschaft, dass ein regelmäßiges n-Eck in mindestens zwei regelmäßige Vielecke zerlegt werden kann.
3,\ 4,\ 6,\ 12
41 J / 31 S
Auf einem 5\times 5-Schachbrett steht in der linken unteren Ecke ein Turm. Der Turm ist eingeschränkt, das heißt, er kann nicht nach links oder nach unten ziehen. Wie viele Möglichkeiten gibt es für den Turm in die rechte obere Ecke zu gelangen?
Dabei werden zwei Wege als unterschiedlich angesehen, wenn die Abfolge der besuchten Felder unterschiedlich ist.
838
42 J / 32 S
Wie lautet die Ziffer an der Hunderterstelle der Zahl 11^{2014} ?
2
43 J / 33 S
Ein Grashüpfer sitzt auf einer Ecke eines gleichseitigen Dreiecks. Bei jedem Sprung wählt der Grashüpfer zufällig eine der beiden anderen Ecken aus und springt zu dieser Ecke.
Wie groß ist die Wahrscheinlichkeit dafür, dass sich der Grashüpfer nach zehn Sprüngen wieder auf der Ecke befindet, von der aus er gestartet ist?
\frac{171}{512}
44 J / 34 S
In einem Computerspiel hat Franz 100 Energieeinheiten, als er anfängt Baumstämme zu zersägen. In jeder Minute kann er sich entscheiden, entweder n Baumstämme zu zersägen und dabei eine Energieeinheit zu verbrauchen, wenn n die Anzahl seiner momentan vorhandenen Energieeinheiten ist, oder zu rasten – und dabei natürlich keine Baumstämme zu zersägen – und eine Energieeinheit aufzunehmen.
Was ist die größte Anzahl an Baumstämmen, die Franz innerhalb von 60 Minuten zersägen kann?
4293
45 J / 35 S
Gegeben sei die Menge \sqrt{\mathbb{N}} = \{\sqrt{1}, \sqrt{2}, \sqrt{3}, \sqrt{4}, \dots \} der Quadratwurzeln aller natürlichen Zahlen. Mit S sei die Menge aller Zahlen a bezeichnet, für die sowohl a \in \sqrt{\mathbb{N}} als auch \frac{36}{a} \in \sqrt{\mathbb{N}} gilt.
Bestimme das Produkt aller Elemente von S.
6^{25}
46 J / 36 S
Wenn man 2014 Ziffern zufällig aus den Ziffern von 0 bis 9 auswählt, wie groß ist dann die Wahrscheinlichkeit, dass ihr Produkt durch 10 teilbar ist?
1-(\frac{5}{10})^{2014} - (\frac{8}{10})^{2014} + (\frac{4}{10})^{2014}
47 J / 37 S
Bestimme den Wert des Ausdrucks
-2002
48 J / 38 S
Boris berechnete die Summe S = 1+2+3+\cdots +2012. Dabei hat er einige Zahlen vergessen und als Ergebnis eine Zahl B erhalten, die durch 2011 teilbar ist. Anna berechnete die Summe A = 1+2+3+\cdots +2013. Dabei hat sie die gleichen Zahlen wie Boris vergessen und erhielt eine Zahl N, die durch 2014 teilbar ist.
Bestimme das Verhältnis \frac NA.
\frac 23
49 J / 39 S
Es liegen 16 Karten mit jeweils einer schwarzen und einer roten Seite in einer Reihe nebeneinander. Ein Zug besteht darin, einen Abschnitt aufeinander folgender Karten umzudrehen, wobei bei der Karte links außen des Abschnitts die schwarze Seite oben ist und bei allen restlichen Karten rechts davon die rote. Das Spiel endet, wenn kein Zug mehr gemacht werden kann.
Bestimme bei einer optimalen Ausgangsstellung die maximal mögliche Anzahl an Zügen, die man machen kann, bevor das Spiel endet.
2^{16}-1
50 J / 40 S
Gesucht sind rechtwinklige Dreiecke mit ganzzahligen Seitenlängen, wobei eine der Katheten die Länge 2014^{14} haben soll.
Wie viele nicht kongruente solche Dreiecke gibt es?
\frac{27\cdot 29^2-1}{2}
51 J / 41 S
Bestimme die kleinste positive Zahl, die nicht als Summe von höchstens 11 Fakultäten geschrieben werden kann. Die Fakultäten müssen dabei nicht unterschiedlich sein.
359
52 J / 42 S
Bei einem Schachturnier spielt jeder Teilnehmer gegen jeden anderen und es gibt keine Unentschieden. Eine Gruppe von vier Schachspielern wird geordnet genannt, wenn es einen klaren Sieger und einen klaren Verlierer in der Gruppe gibt, das heißt, wenn ein Spieler der Gruppe gegen alle drei anderen gewonnen hat und ein Spieler gegen alle drei anderen verloren hat.
Bestimme die kleinste Zahl n, für die jedes Schachturnier mit n Spielern eine geordnete Gruppe besitzt.
8
53 J / 43 S
Zwei einstellige Zahlen aus der Menge \{1, 2, \ldots, 9\} werden ausgewählt. Peter wird das Produkt der beiden Zahlen gesagt und Dominik ihre Summe. Dann entsteht folgendes Gespräch:
- Peter: „Ich kenne die Zahlen nicht.“
- Dominik: „Ich kenne die Zahlen nicht.“
- Peter: „Ich kenne die Zahlen nicht.“
- Dominik: „Ich kenne die Zahlen nicht.“
- Peter: „Ich kenne die Zahlen nicht.“
- Dominik: „Ich kenne die Zahlen nicht.“
- Peter: „Ich kenne die Zahlen nicht.“
- Dominik: „Ich kenne die Zahlen nicht.“
- Peter: „Jetzt kenne ich die Zahlen.“
Welche Zahlen waren ausgewählt worden?
2 und 8
54 J / 44 S
Drei identische Kreiskegel stehen in einer Ebene und berühren sich paarweise. Eine Kugel wird so zwischen die Kegel gelegt, dass der höchste Punkt der Kugel auf der gleichen Höhe liegt wie die Spitzen der Kegel.
Wie groß ist der Radius der Kugel, wenn jeder Kegel eine Grundfläche mit Radius 50\,{\rm cm} und eine Höhe von 120\,{\rm cm} besitzt?

\frac{200\sqrt 3}{9}
55 J / 45 S
Die Zeilen eines 7 \times 7-Gitters werden mit 1, 2, \ldots , 7 durchnummeriert und die Spalten mit A, B, \ldots , G.
Auf wie viele Arten kann man Spielsteine in acht Felder setzen, so dass für je zwei Spielsteine entweder der Abstand ihrer Zeilen oder ihrer Spalten mindestens drei ist?
51
56 J / 46 S
Gegeben seien drei nicht kollineare Punkte A,\ B und C, wobei die Strecke AB durch die Punkte D und E in drei gleiche Teile geteilt wird. Außerdem sei F der Mittelpunkt der Strecke AC und die Strecken EF bzw. BF schneiden die Strecke CD in den Punkten G bzw. H.
Bestimme die Fläche F_{\triangle FGH} des Dreiecks \triangle FGH, wenn F_{\triangle DEG} = 18 ist.
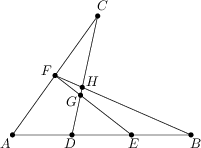
\frac{9}{5}
57 J / 47 S
Die Oberfläche eines Körpers besteht aus zwei gleichseitigen Dreiecken mit Seitenlänge 1 und aus sechs gleichschenkligen Dreiecken mit Schenkellänge x und Basislänge 1 wie in der Abbildung.
Bestimme x, wenn das Volumen des Körpers 6 ist.
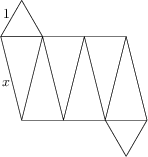
\frac{5\sqrt {39}}{3}























