1 J
Piotr ma sztabkę złota o rozmiarach 2 \times 3 \times 4. Jako początkujący kowal stopił sztabkę i z płynnego złota stworzył trzy jednakowe sześciany. Jaka jest długość krawędzi sześcianów Piotra?
2
2 J
W noworocznych obchodach uczestniczyły 43 osoby. Bar sprzedawał sok, piwo i szampana. Podczas nocy 25 osób piło piwo, 19 osób piło szampana, a 12 osób piło równocześnie piwo i szampana. Pozostali byli kierowcami, więc pili jedynie sok. Nikt nie mieszał soku z piwem lub szampanem. Ile osób piło tylko sok?
11
3 J
Pijąc jedną szklankę czarnej herbaty zyskuje się kofeinę na 1 godzinę. Pijąc jedną szklankę kawy zyskuje się kofeinę na 4 godziny. W jakim stosunku należy wymieszać czarną herbatę i kawę, by uzyskać pełną szklankę zawierającą kofeinę na 2 godziny?
2:1
4 J
Przedstawione na obrazku lustra v i h są do siebie prostopadłe. Kąt między lustrami h i s ma miarę 75 stopni. Promień światła padł na lustro v pod kątem 50 stopni. Następnie odbił się od luster h i s w tej kolejności. Pod jakim kątem padnie teraz na lustro v, jeśli kąt odbicia jest zawsze równy kątowi padania?
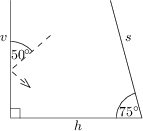
80
5 J
W 2013 roku sklep sprzedał 235 międzygalaktycznych statków kosmicznych. W każdym miesiącu sprzedano 20, 16 lub 25 sztuk. Oblicz w ilu miesiącach sklep sprzedał dokładnie odpowiednio 20, 16 i 25 międzygalaktycznych statków kosmicznych.
4, 5, 3
6 J
Dwa okręgi mają promienie 5 i 26. Mniejszy z nich przechodzi przez środek większego. Rozważmy najdłuższą i najkrótszą cięciwę większego okregu spośród tych, które są styczne do mniejszego okręgu. Jaka jest ich różnica długości?
4
7 J
Collin Farrel urodził się w poprzednim wieku w Sennej Kotlinie. Wiemy, że jego wiek w 1999 roku był taki sam jak suma cyfr roku jego urodzenia. W którym roku urodził się Collin Farrel?
1976
8 J
Ciasna opaska jest naciągnięta na cztery koła o promieniu 1, które są parami styczne (oprócz górnego i dolnego), jak na diagramie poniżej. Jaka jest długość opaski?
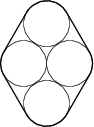
8+2\pi
9 J
Nauczyciel pewnego sportu zawsze ustawia swoją klasę robaków zgodnie z liczbą nóg, które posiadają, od najmniejszej do największej. W ostatnich zawodach uczestniczyli robak Robcio oraz cztery inne robaki, które miały odpowiednio 6, 3, 10 i 9 nóg. Wiemy, że kiedy byli ustawieni w odpowiedniej kolejności, środkowy robak miał tyle samo nóg, ile wynosiła średnia liczba nóg całej piątki robaków. Wyznacz wszystkie możliwe liczby nóg Robcia.
2, 7, 17
10 J
Dla niezerowych cyfr X i Y przez \overline{XY} oznaczamy liczbę, której reprezentacja w systemie dziesiętnym to XY. Wiedząc, że niezerowe cyfry A, B, C spełniają równość \overline{AA} + \overline{BB} + \overline{CC} = \overline{ABC}, wyznacz \overline{ABC}.
198
11 J / 1 S
Słynny kolekcjoner ciał niebieskich Buggo z powodu kryzysu ekonomicznego zmuszony był do sprzedaży jednej trzeciej swojej kolekcji. Zaraz po tym oddał córce 3 planety układu słonecznego. Nieco później odsprzedał jedną trzecią swojej pozostałej kolekcji, a następnie przekazał żonie dwa księżyce Jowisza i dwa ksieżyce Saturna. Kiedy ponownie sprzedał jedną trzecią swoich pozostałych ciał niebieskich oraz Marsa z dwoma księżycami, w jego kolekcji pozostało tylko 9 planet systemu Alfa Centauri. Ile ciał niebieskich Buggo miał na początku?
54
12 J / 2 S
Wyznacz najmniejszą liczbę całkowitą większą niż 2014, której nie można zapisać jako sumy dwóch palindromów.
Uwaga: Palindrom to liczba, która jest taka sama czytana od lewej do prawej i od prawej do lewej.
2019
13 J / 3 S
Vodka dał Ondrowi zagadkę numeryczną. Wybrał cyfrę X i powiedział „Myślę o trzycyfrowej liczbie podzielnej przez 11. Cyfrą setek jest X, a cyfrą dziesiątek 3. Znajdź cyfrę jedności.” Ondro szybko zorientował się, że został oszukany i nie ma takiej liczby. Jaką cyfrę X wybrał Vodka?
4
14 J / 4 S
Cztery liczby rzeczywiste a, b, c, d spełniają warunek a < b < c < d. Jeśli rozważymy wszystkie sześć możliwych par tych liczb i policzymy ich sumy, otrzymamy sześć różnych liczb, spośród których najmniejsze cztery to 1, 2, 3 i 4. Wyznacz wszystkie możliwe wartości liczby d.
3.5, 4
15 J / 5 S
Jack ma dwa razy więcej lat niż Jill miała, gdy Jack był w obecnym wieku Jill. Kiedy Jill będzie w obecnym wieku Jacka, będą mieć w sumie 90 lat. Ile lat ma Jack?
40
16 J / 6 S
Liczby całkowite dodatnie a_1 , a_2 , a_3, \ldots tworzą ciąg arytmetyczny. Jeśli a_1 = 10 oraz a_{a_2} = 100, to jaką wartość ma a_{a_{a_3}}?
820
17 J / 7 S
Ulubiona liczba Natalii posiada wszystkie poniższe własności:
- ma 8 różnych cyfr;
- jej cyfry czytane od lewej do prawej występują w kolejności malejącej;
- jest podzielna przez 180.
Jaka jest ulubiona liczba Natalii?
97654320
18 J / 8 S
Kika lubi budować modele trójwymiarowych brył z papieru w kratkę. Ostatnim razem wycięła kształt przedstawiony na obrazku poniżej. Następnie skleiła go w taki sposób, że żadne dwa kwadraty się nie pokrywały, utworzona bryła nie miała dziur oraz miała niezerową objętość. Ile wierzchołków miała bryła, którą złożyła Kika?
Uwaga: Za wierzchołki uznajemy wierzchołki otrzymanej bryły, a nie punkty kratowe papieru.
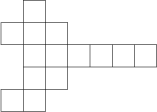
12
19 J / 9 S
Wyznacz wszystkie takie pary dodatnich liczb całkowitych a,b, że ab = \NWD(a,b) + \NWW(a,b), gdzie \NWD(a,b) to największy wspólny dzielnik liczb a i b, a \NWW(a,b) to najmniejsza wspólna wielokrotność liczb a i b.
(2, 2)
20 J / 10 S
Żaba porusza się po przedstawionym poniżej diagramie składającym się 29 kwadratów jednostkowych. W każdym kroku skacze albo do kwadratu przylegającego powyżej (jeśli taki istnieje), albo do kwadratu znajdującego się bezpośrednio powyżej i po prawej od jej obecnej pozycji (jeśli taki istnieje). Żaba zaczyna w jednym z pięciu kwadratów w dolnym rzędzie i skacze dopóki nie dojdzie do górnego rzędu. Ile różnych ścieżek od dolnego do górnego rzędu może obrać żaba?
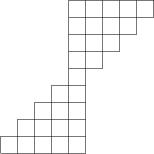
256
21 J / 11 S
Palo chodzi wzdłuż przekątnych ośmiokąta foremnego. Jego spacer zaczyna się w wierzchołku ośmiokąta i prowadzi przez wszystkie przekątne tak, że po każdej z nich przechodzi dokładnie raz. Ile różnych takich spacerów może zrobić Palo?
0
22 J / 12 S
Krata G składająca się z 2014 \times 2014 pól jednostkowych ma lewy dolny róg położony w punkcie o współrzędnych (0, 0), a prawy górny róg w (2014,2014). Prosta p przechodzi przez punkty o współrzędnych (0, 0) i (2014, 2019). Ile pól jednostkowych G przecina prosta p?
Uwaga: Prosta przecina pole jeśli ma co najmniej dwa punkty wspólne z nim. Na przykład przekątna kraty G przecina 2014 pól jednostkowych.
4023
23 J / 13 S
Wypukły n-kąt ma jeden kąt o pewnej mierze, a wszystkie pozostałe n-1 kątów ma miarę 150 stopni. Jakie są możliwe wartości liczby n? Wypisz wszystkie możliwości.
8, 9, 10, 11, 12
24 J / 14 S
Jeśli boki a, b, c trójkąta spełniają równość to jaki jest kąt pomiędzy bokami b i c?
60^{\circ}
25 J / 15 S
Wyznacz wszystkie liczby całkowite między 1 a 200, których różne dzielniki pierwsze sumują się do 16. Przykładowo, suma różnych dzielników pierwszych liczby 12 to 2 + 3 = 5.
66, 132, 198, 55, 39, 117
26 J / 16 S
Długości boków na diagramie spełniają równości DA = AB = BE, GA = AC = CF i IC = CB = BH. Co więcej, EF = DI=5 i GH = 6. Jakie jest pole trójkąta ABC?
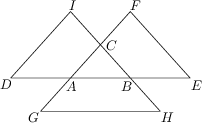
3
27 J / 17 S
Liczbę pierwszą p nazwiemy mocną jeśli jeden z poniższych warunków jest spełniony:
- p jest jednocyfrowa; lub
- usuwając pierwszą cyfrę p uzyskujemy mocną liczbę pierwszą oraz usuwając ostatnią cyfrę p uzyskujemy mocną liczbę pierwszą.
Przykładowo, 37 jest mocną liczbą pierwszą, gdyż usuwając jej pierwszą cyfrę otrzymujemy 7, usuwając ostatnią cyfrę dostajemy 3, a obie liczby 3 i 7 są mocnymi liczbami pierwszymi. Znajdź wszystkie mocne liczby pierwsze.
2, 3, 5, 7, 23, 37, 53, 73, 373
28 J / 18 S
Niech k i l będą dwoma okręgami o promieniu 16 takimi, że każdy z nich przechodzi przez środek drugiego, a p prostą łączącą środki tych okręgów. Okrąg m jest wewnętrznie styczny do okregów k i l oraz do prostej p. Wyznacz długość promienia okręgu m.
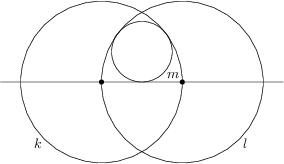
6
29 J / 19 S
Ile jest sześciocyfrowych liczb całkowitych dodatnich, w których każda cyfra występuje tyle razy, jaka jest wartość tej cyfry? Przykładem takiej liczby jest 133232.
82
30 J / 20 S
By potwierdzić swoją reputację fajnego człowieka, E.T. skleił ze sobą cztery kule o promieniu 1 tak, że były parami styczne. Jaki jest promień najmniejszej sfery, która zawiera wszystkie cztery kule E.T.?
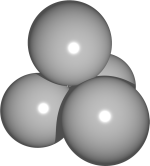
1 + \frac{\sqrt{6}}{2}
31 J / 21 S
Wyznacz liczbę par liczb całkowitych dodatnich (x, y) spełniających y < x \leq 100 takich, że liczby x^2 - y^2 i x^3 - y^3 są względnie pierwsze.
99
32 J / 22 S
Rozważmy liczbę zaczynającą się od 122333444455555 \ldots i kontynuowaną w taki sposób, że każdą liczbę naturalną wypisujemy tyle razy ile wynosi jej wartość. Zatrzymujemy się po napisaniu 2014 cyfr. Jaka jest ostatnia cyfra tej liczby?
4
33 J / 23 S
Jaka jest najmniejsza liczba całkowita dodatnia N, dla której równanie (x^2 - 1)(y^2 - 1) = N ma co najmniej 2 różne rozwiązania takie, że 0<x\leq y oraz x i y są liczbami całkowitymi?
360
34 J / 24 S
Dwa okręgi o promieniach 1 i 3 są styczne w punkcie A. Ich wspólna styczna (nieprzechodząca przez A) jest styczna do nich w punktach B i C. Wyznacz wartość wyrażenia AB^2+BC^2+AC^2.
24
35 J / 25 S
Znajdź największą taką liczbę pierwszą p, że p^p \mid 2014!.
43
36 J / 26 S
Rozważmy tabelę składającą się z 2 kolumn i 2014 wierszy. Iloma sposobami można tę tabelę pomalować 3 kolorami tak, aby żadne dwie komórki o wspólnej krawędzi nie miały tego samego koloru?
6 \cdot 3^{2013}
37 J / 27 S
Znajdź najmniejszą liczbę całkowitą dodatnią m, dla której 5m jest piątą potęgą liczby całkowitej, 6m jest szóstą potęgą liczby całkowitej, a 7m jest siódmą potęgą liczby całkowitej.
5^{84}6^{35}7^{90}
38 J / 28 S
Składamy prostokątną kartkę papieru w taki sposób, żeby dwa przeciwległe rogi (po przekątnej) pokryły się, tworząc w ten sposób zgięcie, czyli odcinek widoczny na papierze. Okazuje się, że długość tego zgięcia jest taka sama jak długość dłuższego boku prostokąta. Jaki jest stosunek długości dłuższego boku do krótszego boku prostokąta?
\sqrt{\frac{1 + \sqrt{5}}{2}}
39 J / 29 S
Mamy 20 kolorowych kuleczek, z których każda jest żółta, niebieska, zielona bądź czerwona. Zakładając, że dwie kuleczki tego samego koloru są nierozróżnialne, ile najwięcej może być niebieskich, jeśli wiadomo, że możemy ułożyć wszystkie kuleczki wzdłuż prostej na dokładnie 1140 różnych sposobów?
17
40 J / 30 S
Znajdź wszystkie liczby całkowite n\ge 3 takie, że n-kąt foremny może być podzielony na (co najmniej dwa) wielokąty foremne.
3, 4, 6, 12
41 J / 31 S
Na szachownicy 5 \times 5 w lewym dolnym rogu stoi wieża. W każdym ruchu może się poruszać tylko w prawo albo tylko w górę o dowolną (niezerową) liczbę pól. Iloma sposobami wieża może dojść do prawego górnego rogu? Dwie drogi uważamy za różne, jeśli ciągi pól, w których zatrzymuje się wieża są różne.
838
42 J / 32 S
Jaka jest cyfra setek liczby 11^{2014}?
2
43 J / 33 S
Konik polny skacze po wierzchołkach trójkąta równobocznego. W każdym ruchu, losowo, z jednakowym prawdopodobieństwem, wybiera jeden z pozostałych dwóch wierzchołków i skacze do niego. Jakie jest prawdopodobieństwo, że w dziesiątym skoku konik polny wróci do wierzchołka, w którym zaczął?
\frac{171}{512}
44 J / 34 S
Kiedy Parsley zaczyna rąbać drzewa ma 100 energii. W każdej minucie może wybrać pomiędzy dwiema możliwościami:
- Wyrąbać n drzew, gdzie n to jego aktualna energia. To go męczy, przez co jego energia spada o 1.
- Odpocząć i zyskać 1 energii. Tak może zrobić dowolnie wiele razy.
Jaka jest maksymalna liczba drzew jaką może Parsley wyciąć w ciągu 60 minut?
4293
45 J / 35 S
Rozważmy zbiór \sqrt{\mathbb{N}} = \{\sqrt{1}, \sqrt{2}, \sqrt{3}, \sqrt{4}, \dots \}, czyli zbiór pierwiastków kwadratowych z liczb całkowitych dodatnich. Niech S będzie zbiorem liczb rzeczywistych a, dla których równocześnie a \in \sqrt{\mathbb{N}} oraz 36/a \in \sqrt{\mathbb{N}}. Jaki jest iloczyn wszystkich elementów zbioru S?
6^{25}
46 J / 36 S
Jakie jest prawdopodobieństwo, że iloczyn losowo wybranych 2014 cyfr będzie podzielny przez 10?
1-(\frac{5}{10})^{2014} - (\frac{8}{10})^{2014} + (\frac{4}{10})^{2014}
47 J / 37 S
Wyznacz wartość wyrażenia Uwaga: \lfloor x \rfloor oznacza największą liczbę całkowitą niewiększą niż x.
-2002
48 J / 38 S
Borys obliczał sumę 1+2+3+\ldots +2012. Jednakże, zapomniał dodać niektórych liczb i otrzymał liczbę podzielną przez 2011. Ania obliczała sumę A = 1+2+3+\ldots +2013, zapomniała dodać tych samych liczb co Borys i otrzymała liczbę N podzielną przez 2014. Jaki jest stosunek N/A?
2/3
49 J / 39 S
Gramy w grę za pomocę 16 kart ułożonych w rzędzie. Każda karta jest z jednej strony czarna, a z drugiej czerwona. Ruch polega na wybraniu grupy sąsiadujących kart (możliwe, że zawierającej tylko 1 kartę), w której karta położona najbardziej z lewej jest czarna, a reszta kart jest czerwona, a następnie obróceniu wszystkich kart z tej grupy na drugą stronę. Gra kończy się gdy nie można już wykonać ruchu. Ile najwięcej ruchów można wykonać w trakcie tej gry?
2^{16} - 1
50 J / 40 S
Trójkąt prostokątny ma wszystkie boki będące liczbami całkowitymi, przy czym jedna z jego przyprostokątnych ma długość 2014^{14}. Ile takich trójkątów istnieje?
\frac{27 \cdot 29^2 - 1}{2}
51 J / 41 S
Jaka jest najmniejsza dodatnia liczba całkowita, która nie może być zapisana jako suma 11 lub mniej (niekoniecznie różnych) silni?
359
52 J / 42 S
W turnieju szachowym każdy z graczy gra przeciwko każdemu innemu dokładnie raz. Ponadto, gracze uzgodnili, że partia nie może się zakończyć remisem. Nazwijmy grupę czterech graczy uporządkowaną jeśli jest w niej wyraźny wygrany i wyraźny przegrany, tj. osoba, która w tej grupie wszystko wygrała i osoba, która wszystko przegrała. Znajdź najmniejszą dodatnią liczbę całkowitą n taką, że każdy turniej z n graczami zawiera grupę czterech graczy, która jest uporządkowana.
8
53 J / 43 S
Wybrałem dwie liczby całkowite ze zbioru \{1,2,\ldots,9\}. Następnie powiedziałem Piotrowi ich iloczyn, a Dominikowi ich sumę. Potem wywiązała się następująca rozmowa:
- Piotr: „Nie wiem, jakie są to liczby.”
- Dominik: „Nie wiem, jakie są to liczby.”
- Piotr: „Nie wiem, jakie są to liczby.”
- Dominik: „Nie wiem, jakie są to liczby.”
- Piotr: „Nie wiem, jakie są to liczby.”
- Dominik: „Nie wiem, jakie są to liczby.”
- Piotr: „Nie wiem, jakie są to liczby.”
- Dominik: „Nie wiem, jakie są to liczby.”
- Piotr: „Już wiem, jakie to są liczby.”
Jakie liczby wybrałem?
2, 8
54 J / 44 S
Na stole stoją trzy jednakowe stożki o parami stycznych podstawach, pomiędzy którymi umieszczono kulę. Kula jest takiej wielkości, że jej najwyższy punkt leży na tej samej wysokości co wierzchołki stożków. Jaki jest promień kuli, jeśli podstawa stożków ma promień równy 50, a ich wysokość wynosi 120?

\frac{200\sqrt{3}}{9}
55 J / 45 S
Wyobraźmy sobie klatkę dla królików utworzoną z 7 \times 7 komórek. Na ile sposobów możemy umieścić tam 8 nierozróżnialnych zrzędliwych królików tak, aby każde dwa króliki były oddalone od siebie o co najmniej 3 komórki w pionie lub co najmniej 3 komórki w poziomie?
36 + 8 + 6 + 1 = 51
56 J / 46 S
Dane są trzy niewspółliniowe punkty A, B i C. Odcinek AB jest podzielony na trzy równe części punktami D i E. Punkt F jest środkiem odcinka AC. Proste EF i BF przecinają prostą CD odpowiednio w punktach G i H. Jakie jest pole \triangle FGH, jeśli pole \triangle DEG wynosi 18?
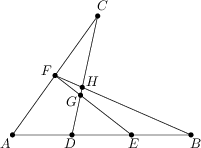
\frac{9}{5}
57 J / 47 S
Powierzchnia pewnej bryły składa się z dwóch trójkątów równobocznych o bokach długości 1 oraz sześciu trójkątów równoramiennych o ramionach długości x i podstawie długoci 1, jak na poniższym obrazku. Jaka jest wartość x, jeśli objętość tej bryły wynosi 6?
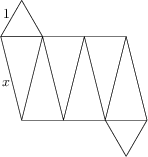
\frac{5\sqrt{39}}{3}