1 J
Little Peter is a cool guy, so he wears only pairs of socks consisting of two socks of different colours. There are 30 red, 40 green, and 40 blue socks in his wardrobe in an unlighted cellar room. Peter takes one sock after the other out of the wardrobe without being able to recognize its colour. What is the minimum number of socks he has to take out if he needs to get eight two-coloured pairs of socks? Note that one single sock must not be counted in two different pairs.
48
2 J
Assume that x and y are positive integers satisfying x^2 + 2y^2 = 2468. Find x if you know that there is only one such pair (x, y) and 1234 = 28^2 + 2 \cdot 15^2.
30
3 J
A digital watch displays time in hours and minutes using the twenty-four hour time format. How many minutes per day can one see the digit 5 on the display?
450
4 J
A big rectangle with perimeter 136\ \text{cm} is divided into seven congruent rectangles as in the picture.
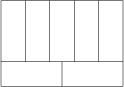
What is the area of the big rectangle in \text{cm}^2?
1120
5 J
A box of chocolates has the shape of an equilateral triangle of side length s\ \text{cm}. There are 2n chocolates in the shape of equilateral triangles, which tightly fill the box: n of side length 1\ \text{cm} and n of side length 2\ \text{cm}. What is the smallest possible value of s?
10
6 J
Little Peter has grown up, so now he wears pairs of socks consisting of two socks of the same colour. He has also got many new socks, so there are currently 20 brown, 30 red, 40 green, 40 blue, 30 black, and 20 white socks in his wardrobe. However, the wardrobe is still situated in an unlighted cellar room. What is the minimum number of socks Peter has to take in order to get eight pairs of socks, if he cannot recognize their colours during the procedure? Note that one single sock must not be counted in two different pairs.
21
7 J
A square and a regular pentagon are inscribed in the same circle and they share a vertex. What is the largest interior angle of the polygon which is the intersection of the two polygons?
153^\circ
8 J
The circle 1 has diameter 48\ \text{mm}. What diameter should the circle 2 have to make the whole mechanism work?
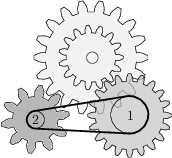
20\ \text{mm}
9 J
For his sixty-two-day summer holiday in July and August, Robert had prepared a precise plan on which days he would lie and on which he would tell the truth. On the k-th day of the holiday (for each k from 1 to 62), he reported that he had planned to lie on at least k days. How many of these statements were lies?
31
10 J
In a game of battleship, our opponent has hidden an aircraft carrier, represented by a 5 \times 1 or 1 \times 5 block, somewhere inside a 9 \times 9 cell grid. What is the smallest number of shots, i.e. choices of a cell in the grid, that is needed to ensure that we have hit the carrier at least once?
16
11 J / 1 S
What is the maximum possible value of a common divisor of distinct positive integers a, b, c satisfying a+b+c=2015?
155
12 J / 2 S
A train supplying an ironworks consists of a locomotive (which is always in the front) and six carriages, each carrying either coal or iron ore. Adam wanted to take a picture of the train, but he failed to capture the whole train, so only an iron ore carriage directly followed by two coal carriages was visible in the photo. The carriages were not completely symmetric, so it was clear that the ore carriage was the first one of these three. How many different trains can be photographed so that one obtains the same picture as Adam did?
31
13 J / 3 S
An object built from several identical cubes looks like ‘1’ from behind, and like ‘3’ from above (see the picture). How many cubes can be seen from the right if we know that the object contains maximum possible number of cubes?
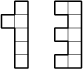
Note: The figure below shows a cube, its back view and its top view, respectively.

17
14 J / 4 S
We say that a positive integer n is delicious if the sum of its digits is divisible by 17 and the same holds for n+10. What is the smallest delicious number?
7999
15 J / 5 S
A bus company runs a line between towns A and D with stops in towns B and C (in this order). The ticket price is directly proportional to the distance travelled by the bus. For example, the ticket from A to C costs the same as the tickets from A to B and from B to C together. Moreover, the company does not offer return tickets, only one way ones. Lisa, a keen bus ticket collector, wants to gather tickets with all possible prices regardless of the direction of the journey. So far she has got the tickets costing 10, 40, 50, 60, and 70. What are the possible prices of the missing ticket?
20, 110
16 J / 6 S
In a clock and watch store, Helen admires a watch which is packed in a transparent rectangular box such that the center of the box and the center of the watch (the point where the hands meet) coincide. The shorter side of the box is 3\ \text{cm} long. She notices that at noon, the hour hand points to the middle of the shorter side of the box, and at one o’clock, it points to the corner of the box. How far apart are the two points on the boundary of the box where the hour hand points to one o’clock and to two o’clock, respectively?
\sqrt 3\ \text{cm}
17 J / 7 S
Find an arrangement of 1,2,\ldots,9 as a nine-digit number such that any two consecutive digits form a number which is a product k\cdot l of digits k, l\in\{1,2,\ldots,9\}.
728163549
18 J / 8 S
Find the largest prime p less than 210 such that the number 210-p is composite.
Note: Recall that number 1 is neither prime nor composite.
89
19 J / 9 S
The management of an elementary school decided to buy a certain number of pencils and to distribute them among the first grade pupils, who were divided into classes A, B, and C. If they gave the same number of pencils to every pupil, each of them would get nine pencils. If they handed them only to class A, each pupil in this class would get 30 pencils, and if they chose class B instead, each would get 36 pencils. How many pencils would a single pupil from class C receive if only this class was given pencils?
20
20 J / 10 S
Find all four-digit square numbers which have the property that both the first two digits and the last two digits are non-zero squares, the latter one possibly starting with zero.
1681
21 J / 11 S
A driver was driving on a highway between two cities at a constant speed. Unfortunately, some parts of the highway were under repair, so he had to reduce his speed by one fourth while he was driving through these sections. Consequently, by the time he would normally have reached his destination, he had travelled only six sevenths of the entire distance. At that point, what fraction of the total time he had been driving did he spend in the sections under repair?
4/7
22 J / 12 S
A rectangle with integral side lengths is decomposed into twelve squares with the following side lengths: 2, 2, 3, 3, 5, 5, 7, 7, 8, 8, 9, 9. What is the perimeter of the rectangle?
90
23 J / 13 S
A square sheet of paper is folded so that one of its vertices is precisely on one of the sides. As in the picture, there is a small triangle, which overlaps the original square. The length of its outer side that is adjacent to the line of the folding is 8\ \text{cm}, and the length of the other outer side is 6\ \text{cm}.
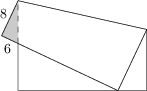
What is the side length of the paper?
36\ \text{cm}
24 J / 14 S
An old steamship is moving along a canal at a constant speed. Simon wants to find out the length of the ship. While the ship is slowly advancing, he walks at the waterside at a constant speed from the rear of the ship to its nose counting 240 steps. Then he immediately turns around and walks backwards up to the rear of the steamship counting 60 steps. What is the length of the steamship in steps?
96
25 J / 15 S
The number 137641=371^2 is the smallest six-digit number such that it is possible to cross out three pairwise different digits to obtain its square root: \cancel137\cancel6\cancel41. Find the largest six-digit number having this property.
992016 = 996^2
26 J / 16 S
Linda typed something on her calculator, and so a three-digit number appeared on the display. Patrick, who was sitting opposite to her, noticed that from his point of view (upside-down) it looked exactly as a three-digit number that is greater by 369 than the one typed. What was the number that Linda typed?
Note: The calculator has a seven-segment display, therefore the digits look like this:

596
27 J / 17 S
There are three families living on the island of Na-boi, each having two sons and two daughters. In how many ways can these twelve people form six married couples if the marriages of siblings are forbidden?
80
28 J / 18 S
Hansel and Gretel have baked a very big pizza consisting of 50 slices of equal circular sector shape. They have distributed olives on the slices in such a way that there are consecutively 1, 2, 3,\ldots, 50 olives placed clockwise on the slices. Now they want to divide the pizza into two equal halves by making a straight cut between the slices so that Hansel gets twice as many olives as Gretel. Determine the total number of olives on the four slices adjacent to the cutting line.
68, 136
29 J / 19 S
Find all primes p with the property that 19p + 1 is the cube of an integer.
421
30 J / 20 S
In a parallelogram ABCD, the point E lies on side AD with 2\cdot AE = ED and the point F lies on side AB with 2\cdot AF = FB. Lines CF and CE intersect the diagonal BD in G and H, respectively. Which fraction of the area of parallelogram ABCD is covered by the area of the pentagon AFGHE?
\frac{7}{30}
31 J / 21 S
Find the largest five-digit number with non-zero digits and the following properties:
- The first three digits form a number which is 9 times the number formed by the last two digits.
- The last three digits form a number which is 7 times the number formed by the first two digits.
85595
32 J / 22 S
Twelve smart men, each of whom was randomly dealt one of twelve cards—nine blank cards and three special cards labelled J, Q, and K—were sitting in a circle. Everybody looked at his card, and then passed it to his right-hand neighbour. Continuing in this way, after every look at a card, they were asked to raise their hands simultaneously if they knew who was holding which special card at that very moment. Nobody raised his hand after having seen four cards. Exactly one man raised his hand after having seen his fifth card. Next, x men raised their hand after having seen six cards and y men after seven cards. Determine xy.
42
33 J / 23 S
Within an isosceles right-angled triangle with the length of the base 1, seven circles are constructed as in the picture:
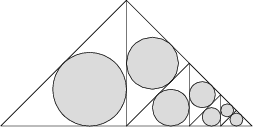
What is the total area of the circles?
\pi \frac{3 - 2\sqrt 2}{4} = \pi\frac{(1-\sqrt2)^2}4 = \pi\frac1{4(1+\sqrt2)^2} = \pi\frac1{4(3+2\sqrt2)}
34 J / 24 S
Find all primes p such that p+11 divides p(p+1)(p+2).
7, 11, 19, 79
35 J / 25 S
Wood lice (Porcellio scaber) have fourteen legs. Mother wood louse has large supplies of identical socks and shoes and prepares her children for the upcoming cold season. She explains to little wood louse Jim that he may put on his socks and shoes in arbitrary order, but he has to bear in mind that on each individual leg he has to put a sock prior to a shoe. In how many ways can little Jim proceed to dress his feet?
\frac{28!}{2^{14}}
36 J / 26 S
Let x be a real number such that x^3 + 4x = 8. Determine the value of x^7 + 64x^2.
128
37 J / 27 S
In an isosceles triangle ABC with base AB, let D be the intersection of angle bisector of \angle ACB with AB and E the intersection of angle bisector of \angle BAC with BC. Given that AE = 2\cdot CD, find \angle BAC.
36^\circ
38 J / 28 S
Given a sequence of real numbers (a_n) such that a_1=2015 and a_1+a_2+\dots+a_n=n^2\cdot a_n for each n \geq 1, find a_{2015}.
\frac1{1008}
39 J / 29 S
Kate and Harriet invented the following game: They colour the faces of two twelve-sided fair dice with cyan, magenta, and yellow so that each colour is present on at least one face of each die, and there are exactly four yellow faces on the first die. If they throw the dice and both of these show the same colour, Kate wins, otherwise Harriet wins. Suppose that the colours are distributed so that the girls have equal chances of winning. How many magenta faces must be there on the second die?
1, 9
40 J / 30 S
There are n > 24 women sitting around a great round table, each of whom either always lies or always tells the truth. Each woman claims the following:
- She is truthful.
- The person sitting twenty four seats to her right is a liar.
Find the smallest n for which this is possible.
32
41 J / 31 S
Two squares have a common center and the vertices of the smaller one lie on the sides of the bigger one. If the small square is removed from the big one, it decomposes into four congruent triangles, the area of each being one twelfth of the area of the big square. What is the size in degrees of the smallest internal angle of the triangles?
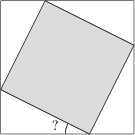
15^\circ
42 J / 32 S
A circle \omega_3 of radius 3 is internally tangent to circles \omega_1, \omega_2 of radii 1 and 2, respectively. Moreover, \omega_1 and \omega_2 are externally tangent. Points A, B on \omega_3 are chosen so that the segment AB is a common external tangent of \omega_1 and \omega_2. Find the length of AB.
\frac43 \sqrt{14}
43 J / 33 S
One day, Oedipus, an intrepid hero, met the Sphinx, who gave him the following riddle: She chose a positive two-digit integer S. Oedipus could choose three one-digit integers a < b < c and ask if S was divisible by them. For each of these numbers, he got an answer (either ‘yes’ or ‘no’). Oedipus fell into despair as there were exactly two numbers satisfying the divisibility conditions. But then the Sphinx told him that she had been wrong about the divisibility by b, which fortunately allowed Oedipus to find S with certainty. What was the value of S?
84
44 J / 34 S
Four people were moving along a road, each of them at some constant speed. The first one was driving a car, the second one was riding a motorcycle, the third one was riding a Vespa scooter, and the fourth one a bicycle. The car driver met the Vespa at 12 noon, the bicyclist at 2 p.m., and the motorcyclist at 4 p.m. The motorcyclist met the Vespa at 5 p.m., and the bicyclist at 6 p.m. At what time did the bicyclist meet the Vespa scooter?
3:20 p.m.
45 J / 35 S
The floor of a hall is covered with a square carpet of side length twenty-two meters. A robotic vacuum cleaner (robovac) is given the task to clean the carpet. For its convenience, the carpet is divided into 484 unit squares. The robovac cleans one square after another in accordance with the following rules:
- Once it has vacuumed a square, it must not move onto it again.
- It keeps moving in one direction unless it is forced to change it by approaching the edge of the carpet or a previously cleaned square.
- If it has to change the direction and there are two options, it may choose whichever it prefers.
At the beginning, the robovac is placed on one square and it may choose any admissible direction. For how many starting squares is the robovac able to clean the whole carpet if it does not need to finish its work on the edge?
20
46 J / 36 S
Let the points A, B, C, D, E, F lie clockwise in this order on a circle \omega. Assume further that AD is a diameter of \omega, BF intersects AD and CE in G and H, respectively, \angle FEH = 56^\circ, \angle DGB = 124^\circ, and \angle DEC = 34^\circ. Find \angle CEB.
22^\circ
47 J / 37 S
Ten people—five women and their husbands—took part in E events. We know that no married couple took part in the same event, every pair of non-married people (including same-sex pairs) took part in exactly one event together, and one person attended only two events. What is the smallest E for which this is possible?
14
48 J / 38 S
Students were given a three-digit number \overline{abc} with 0 < a < b < c. The task was to multiply it by 6 and then swap the tens digit with the hundreds digit. Alex made a mistake and performed the swap before the multiplication, but the result turned out to be correct! Find \overline{abc}.
678
49 J / 39 S
Consider a 5 \times 3 grid. A mouse sitting in the upper left corner wants to reach a piece of cheese in the lower right corner, whereas a crab sitting in the lower left corner wants to reach algae in the upper right corner. They move simultaneously. Every second, the mouse moves one square right or down, and the crab moves one square right or up. In how many ways can the animals reach their food so that they do not meet at all?
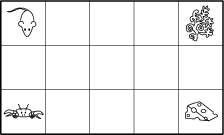
70
50 J / 40 S
Find the number of positive integers n not exceeding 1000 such that the number \lfloor\sqrt[3]{n}\rfloor is a divisor of n.
Note: The symbol \lfloor x\rfloor denotes the integral part of x, i.e. the greatest integer not exceeding x.
172
51 J / 41 S
Find all real m such that the roots of the equation are side lengths of a right-angled triangle.
281/2
52 J / 42 S
There are green and red apples in a basket, at least one red and two green ones. The probability that a randomly chosen apple is red is 42 times higher than the probability that two randomly chosen apples (without replacement) are both green. How many green apples and how many red apples are there in the basket?
4 green and 21 red
53 J / 43 S
Gilbert Bates, a very rich man, wants to have a new swimming pool in his garden. Since he likes symmetry, he tells the gardener to build an elliptical-shaped pool within a 10\ \text{m}\times 10\ \text{m} square ABCD. This elliptical pool should touch all four sides of the square, particularly the side AB at point P which is 2.5\ \text{m} away from A. The gardener, who knows very well how to construct an ellipse if the foci and a point on the ellipse are given, reflects that due to symmetry he only needs the distance of the foci in this case. Can you help him by computing the distance of the foci in meters?
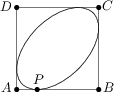
10
54 J / 44 S
A sequence (a_n) is given by a_1=1, and a_n=\lfloor\sqrt{a_1+a_2+\dots+a_{n-1}}\rfloor for n > 1. Determine a_{1000}.
Note: The symbol \lfloor x\rfloor denotes the integral part of x, i.e. the greatest integer not exceeding x.
495
55 J / 45 S
Determine the number of 4 \times 4 tables with non-negative integer entries such that
- every row and every column contains at most two non-zero entries,
- for each row and column, the sum of its entries is 3.
576