1 J
Malý Péťa je velký drsňák a nosí vždy jen ponožky různých barev. Ve skříni má 30 červených, 40 zelených a 40 modrých ponožek. Tato skříň se však nachází ve sklepě v místech, kde se nesvítí, takže když Péťa vytáhne nějakou ponožku, nedovede rozeznat její barvu. Kolik nejméně ponožek musí vytáhnout, aby mezi nimi bylo určitě aspoň osm různobarevných párů? Jedna ponožka může být započítána nejvýše v jednom páru.
48
2 J
Nechť x a y jsou kladná celá čísla vyhovující rovnici x^2 + 2y^2 = 2468. Určete x, jestliže víte, že řešením rovnice je pouze jedna dvojice (x,y) a že 1234 = 28^2 + 2 \cdot 15^2.
30
3 J
Digitální hodinky ukazují čas v hodinách a minutách ve dvacetičtyřhodinovém formátu. Kolik minut denně se na jejich displeji vyskytuje aspoň jedna pětka?
450
4 J
Obdélník o obvodu 136\ \text{cm} je rozdělen na sedm shodných obdélníčků jako na obrázku.
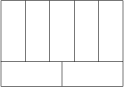
Jaký je obsah tohoto obdélníka v \text{cm}^2?
1120
5 J
Bonboniéra má tvar rovnostranného trojúhelníka o straně délky s\ \text{cm} a obsahuje 2n bonbónů ve tvaru rovnostranného trojúhelníka – n o straně 1\ \text{cm} a n o straně 2\ \text{cm}. Bonbóny jsou naskládané těsně vedle sebe tak, aby zaplnily celou bonboniéru. Jaká je nejmenší možná hodnota s?
10
6 J
Malý Péťa vyrostl, i nosí už jen ponožky stejných barev. Navíc dostal mnoho nových ponožek, takže nyní má ve skříni 20 hnědých, 30 červených, 40 zelených, 40 modrých, 30 černých a 20 bílých ponožek. Skříň je však stále ve sklepě, kde není žádné světlo, a Péťa tak není schopen rozeznat barvy ponožek. Kolik nejméně ponožek musí ze skříně vzít, aby měl jistotu, že mezi nimi bude osm párů? Jednu ponožku lze samozřejmě započítat nejvýše do jednoho páru.
21
7 J
Čtverec a pravidelný pětiúhelník mají společnou kružnici opsanou a sdílejí vrchol. Jak velký je největší vnitřní úhel mnohoúhelníka, který je jejich průnikem?
153^\circ
8 J
Kolem koleček 1 a 2 je natažen řemen. Kolečko 1 má průměr 48\ \text{mm}. Jaký průměr musí mít kolečko 2, pokud má celý mechanismus fungovat?
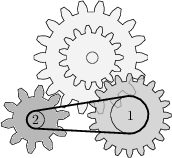
20\ \text{mm}
9 J
Honza si na své dvaašedesátidenní prázdniny v červenci a srpnu připravil přesný plán, které dny bude lhát a které dny bude mluvit pravdu. V k-tém dni (pro každé k od 1 do 62) pak prohlásil, že měl v plánu lhát aspoň k dní. Kolik z těchto výpovědí bylo lživých?
31
10 J
Šavlík s Filipem hráli lodě ve čtverci 9 \times 9. Šavlík někam umístil letadlovou loď o rozměrech 5\times1, resp. 1\times 5. Jaký je nejmenší počet polí, do nichž musí Filip vystřelit, aby loď s jistotou zasáhl?
16
11 J / 1 S
Jaká je největší možná hodnota společného dělitele po dvou různých kladných celých čísel a, b, c splňujících vztah a+b+c=2015?
155
12 J / 2 S
Vlak zásobující továrnu sestává z lokomotivy (která je vždy na začátku) a šesti vagónů, z nichž každý veze buď železnou rudu, nebo uhlí. David chtěl takový vlak vyfotografovat, ale podařilo se mu zachytit jen tři sousední vagóny. První – ten z nich, který byl nejblíže lokomotivě – vezl železnou rudu a následující dva vezly uhlí. Kolik různých vlaků mohl David takto vyfotografovat?
31
13 J / 3 S
Útvar slepený z několika stejně velkých krychliček vypadá zezadu jako jednička a shora jako trojka, viz obrázek. Navíc víme, že obsahuje maximální možný počet krychliček. Kolik z nich je vidět při pohledu zprava?
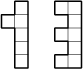
Poznámka: Následující obrázek ilustruje pohled zezadu a pohled shora na průhledné krychli.

17
14 J / 4 S
Řekneme, že přirozené číslo n je lahodné, jestliže ciferný součet n i n+10 je dělitelný sedmnácti. Jaké je nejmenší lahodné číslo?
7999
15 J / 5 S
Autobusová doprava provozuje linku mezi městy A a D s mezizastávkami v městech B a C (v tomto pořadí). Cena jízdenky je přímo úměrná vzdálenosti, kterou autobus urazí, tedy například jízdenka z A do C stojí stejně jako jízdenky z A do B a z B do C dohromady. Prodávají se přitom pouze jednosměrné jízdenky. Tonda je vášnivý sběratel a rozhodl se do své sbírky získat jízdenky všech možných cen (stačí mu od každé ceny jedna). Zatím má jízdenky o cenách 10, 40, 50, 60 a 70. Jaké jsou možné ceny poslední jízdenky?
20, 110
16 J / 6 S
Vejtek v hodinářství obdivuje hodinky zabalené v ploché průhledné krabičce obdélníkového tvaru. Všiml si, že střed hodinek (místo, kde se setkávají hodinová a minutová ručička) je přesně ve středu krabičky. Navíc zpozoroval, že v poledne ukazuje malá ručička do středu kratší strany krabičky, zatímco v jednu hodinu ukazuje přesně do rohu. Jak daleko jsou od sebe body na hranici krabičky, na něž ukazuje malá ručička v jednu a ve dvě hodiny? Délka kratší strany krabičky je 3\ \text{cm}.
\sqrt 3\ \text{cm}
17 J / 7 S
Najděte devíticiferné číslo, které obsahuje každou z cifer 1,2,\ldots,9 právě jednou, a navíc každé dvě jeho sousední cifry tvoří dvojciferné číslo, jež je součinem k\cdot l dvou čísel k, l\in\{1,2,\ldots,9\}.
728163549
18 J / 8 S
Najděte největší prvočíslo p menší než 210 takové, že číslo 210-p je složené.
Poznámka: Připomeňme, že jednička není ani prvočíslo, ani číslo složené.
89
19 J / 9 S
Základní škola se rozhodla nakoupit spoustu tužek pro prvňáky, rozdělené do tříd A, B a C. Kdyby se tužky rozdaly spravedlivě ve všech třídách, dostal by každý žáček devět tužek. Pokud by se rozdaly jen ve třídě A, dostal by jich každý 30, a pokud jen ve třídě B, měl by každý 36. Kolik tužek by dostal každý žáček ve třídě C, kdyby se tužky rozdaly jen tam?
20
20 J / 10 S
Najděte všechny čtyřciferné čtverce, jejichž první i druhé dvojčíslí jsou nenulové čtverce (druhý z nich může začínat nulou).
Poznámka: Čtvercem rozumíme druhou mocninu nějakého celého čísla.
1681
21 J / 11 S
Řidič jel konstantní rychlostí po dálnici vedoucí mezi dvěma městy. Bohužel se některé úseky dálnice opravovaly, a tak byl nucen při průjezdu těmito místy snížit rychlost o čtvrtinu. V čase, kdy by obyčejně dorazil do cíle, měl proto za sebou teprve šest sedmin celkové vzdálenosti. Jaký zlomek celkového času strávil do této chvíle v opravovaných úsecích?
4/7
22 J / 12 S
Obdélník s celočíselnými délkami stran je rozřezán na dvanáct čtverců, které mají délky stran 2, 2, 3, 3, 5, 5, 7, 7, 8, 8, 9, 9. Jaký je obvod tohoto obdélníka?
90
23 J / 13 S
Čtvercový list papíru je přeložen tak, že se jeden z jeho vrcholů dotýká jedné z protějších stran jako na obrázku. V trojúhelníčku přesahujícím obrys původního čtverce má delší z vnějších stran (sousedící s přehybem) délku 8\ \text{cm} a kratší z nich má délku 6\ \text{cm}.
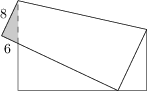
Jaká je délka strany papíru?
36\ \text{cm}
24 J / 14 S
Starý křižník pluje konstantní rychlostí po kanálu. Štěpána by zajímalo, jak je dlouhý. Zatímco se loď pomalu pohybuje vpřed, kráčí Štěpán konstantní rychlostí po břehu od zádi až k přídi, přičemž napočítá 240 kroků. Poté se hned otočí a kráčí zpět k zádi, což mu vyjde na 60 kroků. Jaká je délka křižníku v krocích?
96
25 J / 15 S
Číslo 137641=371^2 je nejmenším šesticiferným číslem, z něhož je možné vyškrtnout tři navzájem různé cifry a dostat tak jeho druhou odmocninu: \cancel137\cancel6\cancel41. Najděte největší šesticiferné číslo s touto vlastností.
992016 = 996^2
26 J / 16 S
Martina naťukala něco do kalkulačky a na displeji se objevilo trojciferné číslo x. Olin, který seděl naproti ní, si všiml, že ze svého pohledu (vzhůru nohama) přečte na displeji přesně číslo, které je o 369 větší než x. Jaké je ono Martinino číslo x?
Poznámka: Kalkulačka má segmentový displej, číslice 0–9 tedy vypadají takto:

596
27 J / 17 S
Na ostrově Na-boi žijí tři rodiny, z nichž v každé mají dva syny a dvě dcery. Kolika způsoby může těchto dvanáct potomků utvořit šest manželských párů, jestliže sňatky sourozenců nejsou přípustné?
80
28 J / 18 S
Jana a Jirka upekli obrovskou pizzu, kterou rozřezali na padesát stejných dílků (kruhových výsečí), a na každý z těchto dílků dali postupně po směru hodinových ručiček 1, 2, 3,\ldots, 50 oliv. Nyní by pizzu chtěli rovným řezem mezi dílky rozdělit napůl tak, aby Jana dostala dvakrát více oliv než Jirka. Jaký bude součet počtu oliv na čtyřech dílcích sousedících s tímto řezem?
68, 136
29 J / 19 S
Najděte všechna prvočísla p, pro která je 19p + 1 třetí mocninou celého čísla.
421
30 J / 20 S
Mějme rovnoběžník ABCD a body E, F postupně na stranách AD, AB takové, že 2 |AE| = |ED| a 2 |AF| = |FB|. Přímky CF a CE protínají úhlopříčku BD postupně v bodech G a H. Jakou část plochy rovnoběžníka ABCD zaujímá pětiúhelník AFGHE?
\frac{7}{30}
31 J / 21 S
Najděte největší pěticiferné číslo s nenulovými ciframi, které má následující vlastnosti:
- První trojčíslí tvoří číslo devětkrát větší než poslední dvojčíslí.
- Poslední trojčíslí tvoří číslo sedmkrát větší než první dvojčíslí.
85595
32 J / 22 S
V kruhu sedělo dvanáct bystrých mužů a každému z nich byla náhodně rozdána jedna z dvanácti karet – devíti prázdných a tří význačných označených jako J, Q a K. Každý z mužů se podíval na svou kartu a poté ji poslal sousedovi po pravé ruce. Takto se pokračovalo dále, přičemž po každém zhlédnutí karty byli všichni v jeden okamžik vyzváni, aby se přihlásili, pokud vědí, kdo právě drží kterou význačnou kartu. V prvních čtyřech kolech se nepřihlásil nikdo a po spatření páté karty zvedl ruku jeden člověk. V následujícím kole, tj. po šesti kartách, se přihlásilo x lidí a v tom dalším y lidí. Určete xy.
42
33 J / 23 S
Uvnitř rovnoramenného pravoúhlého trojúhelníka, jehož základna má délku 1, bylo sestrojeno sedm kružnic jako na následujícím obrázku:
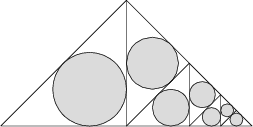
Jaký je součet jejich obsahů?
\pi \frac{3 - 2\sqrt 2}{4} = \pi\frac{(1-\sqrt2)^2}4 = \pi\frac1{4(1+\sqrt2)^2} = \pi\frac1{4(3+2\sqrt2)}
34 J / 24 S
Najděte všechna prvočísla p taková, že p+11 dělí p(p+1)(p+2).
7, 11, 19, 79
35 J / 25 S
Stínka obecná (Porcellio scaber) má čtrnáct nohou. Maminka stínka má velké zásoby stejných ponožek a bot a připravuje své děti na nadcházející chladné období. Vysvětluje malému Kubovi, že ponožky i boty si může obout v libovolném pořadí, ale na každou nohu si musí dát nejprve ponožku a až pak botu. Kolika způsoby se může Kuba obout?
\frac{28!}{2^{14}}
36 J / 26 S
Nechť x je reálné číslo splňující x^3 + 4x = 8. Jaká je hodnota výrazu x^7 + 64x^2?
128
37 J / 27 S
V rovnoramenném trojúhelníku ABC se základnou AB buď D průsečík osy úhlu ACB s AB a E průsečík osy úhlu BAC s BC. Víte-li, že |AE| = 2 |CD|, určete |\sphericalangle BAC|.
36^\circ
38 J / 28 S
Je dána posloupnost reálných čísel (a_n) splňující a_1=2015 a a_1+a_2+\dots+a_n=n^2\cdot a_n pro všechna n \geq 1. Určete a_{2015}.
\frac1{1008}
39 J / 29 S
Míša s Aničkou vymyslely hru. Obarvily stěny dvou dvanáctistěnných kostek azurovou, purpurovou a žlutou barvou tak, aby na každé kostce byla aspoň jedna stěna každé z těchto barev a na první z nich byly právě čtyři stěny žluté. Jestliže nyní hodí oběma kostkami a padnou na nich stejné barvy, vyhrává Míša, v opačném případě vyhrává Anička. Kolik purpurových stěn je na druhé kostce, mají-li obě děvčata stejnou šanci na výhru?
1, 9
40 J / 30 S
Okolo kulatého stolu sedí n > 24 žen, z nichž každá buď vždy lže, nebo vždy mluví pravdu. Navíc každá z těchto žen tvrdí následující:
- „Já mluvím pravdu.“
- „Odpočítám-li 24 židlí po mé pravici, tak na té 24. sedí lhářka.“
Najděte nejmenší n, pro které tato situace může nastat.
32
41 J / 31 S
Dva čtverce mají společný střed, přičemž vrcholy menšího z nich leží na stranách většího. Vystřihneme-li menší čtverec z většího, zbydou nám čtyři shodné trojúhelníky, z nichž každý má obsah rovný jedné dvanáctině obsahu většího čtverce. Jaká je velikost nejmenšího vnitřního úhlu těchto trojúhelníků ve stupních?
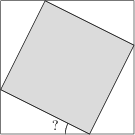
15^\circ
42 J / 32 S
Kružnice \omega_3 o poloměru 3 má vnitřní dotyk s kružnicí \omega_1 o poloměru 1 a kružnicí \omega_2 o poloměru 2, přičemž \omega_1 a \omega_2 mají vnější dotyk. Na \omega_3 leží body A, B takové, že úsečka AB je vnější společnou tečnou kružnic \omega_1 a \omega_2. Spočtěte délku úsečky AB.
\frac43 \sqrt{14}
43 J / 33 S
Jednoho dne potkal nebojácný Oidipus Sfingu, která mu položila hádanku. Vymyslela si dvojciferné číslo S a následně umožnila Oidipovi vybrat tři různá jednociferná čísla a<b<c a pro každé z nich se zeptat, zda je jím S dělitelné. Poté, co Oidipus obdržel tři odpovědi ano/ne, měl číslo S uhádnout. Upadl však do zoufalství, neboť tyto podmínky splňovala právě dvě různá čísla. Naštěstí mu Sfinga krátce nato sdělila, že se spletla v dělitelnosti b, což mu umožnilo číslo S s jistotou určit. Jaké bylo číslo S?
84
44 J / 34 S
Po silnici se pohybovaly čtyři dopravní prostředky – auto, motocykl, skútr Vespa a kolo. Každý z nich jel nějakou konstantní rychlostí. Auto se v pravé poledne minulo s Vespou, ve dvě hodiny odpoledne s kolem a ve čtyři odpoledne s motocyklem. Motocykl potkal v pět odpoledne Vespu a v šest večer kolo. V kolik hodin se setkala Vespa s kolem?
15:20
45 J / 35 S
Podlaha haly je pokryta čtvercovým kobercem o straně délky 22 metrů, který je rozdělen na 484 jednotkových čtverců. Robotický vysavač dostal za úkol koberec vysát. Vysává jeden čtverec za druhým podle následujících pravidel:
- Jakmile vysaje nějaký čtverec, už se na něj nikdy nevrátí.
- Pohybuje se jedním směrem, dokud není nucen jej změnit buď kvůli tomu, že dorazil na okraj koberce, nebo proto, že mu v cestě stojí již vysátý čtverec.
- Kdykoliv je nucen změnit směr a má dvě možnosti, sám zvolí jednu z nich.
Robotický vysavač začíná na některém jednotkovém čtverci a může si vybrat libovolný z kolmých směrů. Skončit může na kterémkoliv čtverci. Pro kolik různých počátečních čtverců je vysavač schopen vysát celý koberec?
20
46 J / 36 S
Body A, B, C, D, E, F leží postupně po směru hodinových ručiček na kružnici \omega, přičemž AD je její průměr. Přímka BF protíná přímky AD a CE postupně v bodech G a H. Předpokládejme, že |\sphericalangle FEH| = 56^\circ, |\sphericalangle DGB| = 124^\circ a |\sphericalangle DEC| = 34^\circ. Spočtěte |\sphericalangle CEB|.
22^\circ
47 J / 37 S
Pět manželských párů se zúčastnilo V večírků. Víme, že na žádném večírku se nepotkali muž a žena tvořící pár, ale každá jiná dvojice (včetně dvojic osob stejného pohlaví) byla společně na právě jednom večírku. Jedna z osob navštívila pouze dva večírky. Pro jaké nejmenší V mohla popsaná situace nastat?
14
48 J / 38 S
Studenti dostali trojciferné číslo \overline{abc} takové, že 0 < a < b < c. Měli za úkol jej vynásobit šesti a poté prohodit cifru na místě stovek s cifrou na místě desítek. Pepa udělal chybu a provedl tyto dvě operace v opačném pořadí. Ukázalo se však, že i přesto dostal správný výsledek! Nalezněte \overline{abc}.
678
49 J / 39 S
Uvažujme mřížku 5 \times 3. V levém horním rohu sedí myš, která chce získat kousek sýra v pravém dolním rohu, a v levém dolním rohu je krab, který si dělá zálusk na řasy v pravém horním rohu. Pohybují se oba současně. Každou sekundu se myš přemístí o jeden čtverec doprava nebo dolů a krab se přesune o jeden čtverec doprava nebo nahoru. Kolika způsoby mohou oba dorazit ke své potravě, aniž by se na nějakém čtverci potkali?
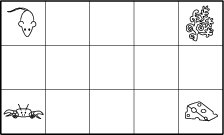
70
50 J / 40 S
Najděte počet kladných celých čísel n nepřevyšujících 1000 takových, že číslo \lfloor\sqrt[3]{n}\rfloor je dělitelem n.
Poznámka: Symbol \lfloor x\rfloor značí dolní celou část x, tj. největší celé číslo nepřevyšující x.
172
51 J / 41 S
Najděte všechna reálná čísla m, pro která jsou kořeny rovnice délkami stran pravoúhlého trojúhelníka.
281/2
52 J / 42 S
V košíku jsou zelená a červená jablka – aspoň jedno červené a aspoň dvě zelená. Pravděpodobnost, že náhodně vybrané jablko bude červené, je 42-krát větší než pravděpodobnost, že dvě různá náhodně vybraná jablka budou obě zelená. Kolik zelených a kolik červených jablek je v košíku?
4 zelená a 21 červených
53 J / 43 S
Gilbert Bates, velmi bohatý člověk, se rozhodl, že si na zahradě nechá postavit bazén ve tvaru elipsy. Sdělil zahradníkovi své přání, že tato elipsa by se měla vejít do čtverce ABCD o rozměrech 10\ \text{m}\times 10\ \text{m}, přičemž by se měla dotýkat všech jeho stran. Je-li navíc P bod dotyku elipsy se stranou AB, pak by vzdálenost bodů A a P měla být 2{,}5\ \text{m}. Zahradník, který umí sestrojit elipsu, má-li danou polohu ohnisek a nějaký bod této elipsy, si uvědomil, že díky symetrii mu v tomto případě stačí znát vzdálenost ohnisek. Jaká je tato vzdálenost v metrech?
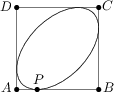
10
54 J / 44 S
Posloupnost (a_n) je zadána rekurentně jako a_1=1 a a_n=\lfloor\sqrt{a_1+a_2+\dots+a_{n-1}}\rfloor pro n > 1. Určete a_{1000}.
Poznámka: Symbol \lfloor x\rfloor značí dolní celou část x, tj. největší celé číslo nepřevyšující x.
495
55 J / 45 S
Určete počet tabulek 4 \times 4, v jejichž políčkách jsou vepsána nezáporná celá čísla taková, že
- v každém řádku a každém sloupci jsou nejvýše dvě nenulová čísla,
- součet čísel každém řádku a v každém sloupci je 3.
576






















