1 J
Klein-Jonas ist ein echt cooler Typ: Er zieht nur Sockenpaare an, bei denen die eine Socke eine andere Farbe hat als die andere. In einem dunklen Kellerraum steht sein Schrank und darin befinden sich im Durcheinander 30 rote, 40 grüne und 40 blaue einzelne Socken. Klein-Jonas nimmt eine Socke nach der anderen aus dem Schrank heraus, ohne dass er ihre Farbe erkennen kann. Was ist die minimale Anzahl an Socken, die er herausnehmen muss, um auf jeden Fall acht Paare an Socken zu erhalten, bei denen die eine Socke eine andere Farbe hat als die andere?
Hinweis: Beachte, dass eine einzelne Socke nicht in zwei verschiedenen Paaren gezählt werden darf.
48
2 J
Es seien x und y zwei positive ganze Zahlen, welche die Gleichung x^2 + 2y^2 = 2468 erfüllen. Finde x, wenn bekannt ist, dass es nur ein einziges solches Paar (x,y) gibt und dass die Gleichung 1234 = 28^2 + 2 \cdot 15^2 gilt.
30
3 J
Eine Digitaluhr im 24-Stunden-Zeitformat zeigt die Uhrzeit in Stunden und Minuten an. Wie viele Minuten pro Tag erscheint die Ziffer 5 mindestens einmal am Display?
450
4 J
Ein großes Rechteck mit dem Umfang 136\ \text{cm} ist, wie in der Abbildung, in sieben kongruente Rechtecke unterteilt.
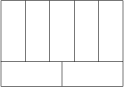
Wie groß ist der Flächeninhalt des großen Rechtecks in \text{cm}^2 ?
1120
5 J
Eine Schokoladenschachtel hat die Form eines gleichseitigen Dreiecks mit der Seitenlänge s\ \mbox{cm}. Die Schachtel ist mit 2n Schokoladenstücken, die alle die Form eines gleichseitigen Dreiecks haben, lückenlos gefüllt: n Stücke haben die Seitenlänge 1\ \mbox{cm} und n haben die Seitenlänge 2\ \mbox{cm}. Was ist der kleinstmögliche Wert für s?
10
6 J
Jonas ist in die Jahre gekommen: Er trägt jetzt nur noch Sockenpaare, bei denen beide Socken die gleiche Farbe haben. Er hat mittlerweile auch viele neue Socken, so dass sich nun 20 braune, 30 rote, 40 grüne, 40 blaue, 30 schwarze und 20 weiße einzelne Socken in seinem Schrank befinden. Allerdings steht sein Schrank immer noch in einem dunklen Kellerraum. Was ist die minimale Anzahl an Socken, die Jonas herausnehmen muss, um mit Sicherheit acht Paar Socken zu erhalten, wenn er beim Herausnehmen der Socken ihre Farbe nicht erkennen kann?
Hinweis: Beachte, dass eine einzelne Socke nicht in zwei verschiedenen Paaren gezählt werden darf.
21
7 J
Gegeben seien ein Quadrat und ein regelmäßiges Fünfeck sowie ein Kreis, auf dem alle Ecken der beiden Vielecke liegen, und zwar so, dass Quadrat und Fünfeck eine gemeinsame Ecke haben. Bestimme den größten Innenwinkel desjenigen Vielecks, das die Schnittfläche der beiden gegebenen Vielecke bildet.
153^\circ
8 J
Kreis 1 hat einen Durchmesser von 48 mm. Welchen Durchmesser muss Kreis 2 haben, damit der gesamte Mechanismus funktioniert?
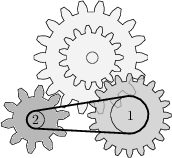
20 mm
9 J
Robert hat für seine 62-tägigen Sommerferien im Juli und August einen genauen Plan vorbereitet, der festlegt, an welchen Tagen er lügen und an welchen Tagen er die Wahrheit sagen wird. Für alle k von 1 bis 62 erklärt er am k-ten Tag seiner Ferien, dass er geplant hat, an mindestens k Tagen zu lügen. Wie viele Lügen waren nach Ablauf der 62 Tage unter seinen Aussagen?
31
10 J
Bei dem Spiel Schiffe versenken hat ein Spieler seinen Flugzeugträger, der aus einem 5 \times 1 – oder einem 1 \times 5 – Block besteht, irgendwo innerhalb eines 9 \times 9 – Gitters versteckt. Wie oft muss sein Gegner mindestens schießen, das heißt ein Feld im Gitter auswählen, damit er den Flugzeugträger mit Sicherheit mindestens einmal getroffen hat?
16
11 J / 1 S
Die Zahlen a, b und c seien paarweise verschiedene positive ganze Zahlen mit a+b+c=2015. Finde den größtmöglichen Wert, den ein gemeinsamer Teiler von a, b und c annehmen kann.
155
12 J / 2 S
Ein Zug, der ein Stahlwerk beliefert, besteht aus einer Lokomotive, die sich immer ganz vorne befindet, und sechs Waggons. Jeder Waggon transportiert entweder Kohle oder Eisenerz. Adam wollte ein Foto des vorbeifahrenden Zuges machen. Anstelle des gesamten Zuges befand sich jedoch nur ein Ausschnitt, bestehend aus drei Waggons, auf dem Foto. Zu sehen ist ein Waggon mit Eisenerz direkt gefolgt von zwei Waggons mit Kohle. Da die Waggons nicht völlig symmetrisch waren, konnte Adam mit Gewissheit sagen, dass der Waggon mit Eisenerz der erste der drei Waggons war. Wie viele verschiedene Züge können fotografiert werden, sodass man dasselbe Foto wie Adam erhält?
31
13 J / 3 S
Ein Körper, der aus mehreren identischen Würfeln besteht, sieht von hinten wie eine ‘1’ und von oben wie eine ‘3’ aus (siehe Abbildung). Wie viele Würfel kann man sehen, wenn man den Körper von rechts betrachtet und man weiß, dass der Körper aus der maximal möglichen Anzahl von Würfeln besteht?
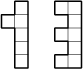
Hinweis: Die folgende Abbildung zeigt einen Würfel, seine Ansicht von hinten bzw. seine Ansicht von oben. Achte auf die genaue Lage der Dreiecke!

17
14 J / 4 S
Eine natürliche Zahl n wird als herrlich bezeichnet, wenn sowohl sie selbst als auch n+10 jeweils eine Quersumme haben, die durch 17 teilbar ist. Bestimme die kleinste herrliche Zahl.
7999
15 J / 5 S
Ein Busunternehmen fährt auf einer Linie zwischen den Städten A und D mit Haltestellen in den Städten B und C (in dieser Reihenfolge). Der Ticketpreis ist direkt proportional zur Entfernung, die der Bus zurücklegt. So kostet beispielsweise das Ticket von A nach C genauso viel wie die Tickets von A nach B und von B nach C zusammen. Das Busunternehmen bietet keine Rückfahrtickets an. Lisa, eine eifrige Fahrkartensammlerin, möchte ohne Rücksicht auf die Fahrtrichtung Tickets mit allen möglichen Preisen sammeln. Bis jetzt hat sie bereits Tickets mit den Preisen 10, 40, 50, 60 und 70. Gib die möglichen Preise des fehlenden Tickets an!
20, 110
16 J / 6 S
Helena bewundert in einem Uhrengeschäft eine Uhr, die so in einer transparenten rechteckigen Schachtel verpackt ist, dass der Mittelpunkt der Schachtel mit dem Mittelpunkt der Uhr – das ist der Punkt, an dem sich die Zeiger treffen – zusammenfällt. Die kürzere Seite der Schachtel ist 3\ \mbox{cm} lang. Helena stellt fest, dass der Stundenzeiger um zwölf Uhr auf den Mittelpunkt der kürzeren Seite und um ein Uhr auf eine Ecke der Schachtel zeigt. Wie weit voneinander entfernt sind die beiden Punkte auf der längeren Begrenzungsseite der Schachtel, auf die der Stundenzeiger um ein Uhr und um zwei Uhr zeigt?
\sqrt 3\ \mbox{cm}
17 J / 7 S
Man ordne die Ziffern von 1 bis 9 so als 9-stellige Zahl an, dass je zwei aufeinander folgende Ziffern eine Zahl bilden, die gleich dem Produkt zweier Zahlen k und l mit k,\, l\in\{1,\ldots ,9\} ist.
728163549
18 J / 8 S
Finde die größte Primzahl p kleiner als 210, sodass die Zahl 210-p zusammengesetzt ist.
Hinweis: Denke daran, dass die Zahl 1 weder prim noch zusammengesetzt ist.
89
19 J / 9 S
Die Leitung einer Grundschule beschloss, eine bestimmte Anzahl an Bleistiften für die Schüler der ersten Jahrgangsstufe, in der es die Klassen A, B und C gibt, anzuschaffen. Wenn sie jedem Schüler die gleiche Anzahl gegeben hätte, so hätte jeder Schüler neun Bleistifte erhalten. Wenn sie die Bleistifte nur in Klasse A verteilt hätte, so hätte jeder Schüler dieser Klasse 30 Bleistifte bekommen. Bei einer Verteilung nur in Klasse B hätte jeder dieser Schüler 36 Bleistifte empfangen. Wie viele Bleistifte hätte ein einzelner Schüler aus Klasse C erhalten, wenn sie nur dort verteilt worden wären?
20
20 J / 10 S
Bestimme alle vierstelligen Quadratzahlen, bei denen die ersten beiden Ziffern und die letzten beiden Ziffern jeweils zweistellige, von Null verschiedene Quadratzahlen sind, wobei letztere aber mit einer Null beginnen darf.
1681
21 J / 11 S
Christian fuhr mit seinem Auto mit konstanter Geschwindigkeit auf der Autobahn von Passau nach Linz. Leider gab es seit kurzer Zeit einige Baustellenbereiche, in denen er seine Geschwindigkeit um ein Viertel verringern musste. Folglich war Christian zu der Zeit, zu der er normalerweise in Linz angekommen wäre, erst sechs Siebtel der Gesamtstrecke gefahren. Welchen Anteil an der Zeit, die er bis zu diesem Zeitpunkt brauchte, fuhr er durch die Baustellenbereiche?
4/7
22 J / 12 S
Ein Rechteck mit ganzzahligen Seitenlängen wird in zwölf Quadrate zerlegt, die folgende Seitenlängen besitzen: 2, 2, 3, 3, 5, 5, 7, 7, 8, 8, 9 und 9. Welchen Umfang hat dieses Rechteck?
90
23 J / 13 S
Ein quadratisches Blatt Papier wird so gefaltet, dass eine der Ecken genau auf der gegenüberliegenden Seite des Quadrats zu liegen kommt. Wie in der Abbildung zu sehen ist, gibt es ein kleines Dreieck, das über das ursprüngliche Quadrat hinausragt. Die außerhalb liegende Seite des kleinen Dreiecks, die an die Faltlinie grenzt, hat eine Länge von 8\ \mbox{cm} und die Länge der anderen außerhalb liegenden Seite ist 6\ \mbox{cm}.
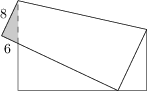
Gib die Seitenlänge des quadratischen Blatt Papiers an!
36 cm
24 J / 14 S
Ein altes Dampfschiff der Donaudampfschifffahrtsgesellschaft fährt gemütlich mit gleichmäßiger Geschwindigkeit den Donau-Kanal entlang. Simon möchte herausfinden, wie lang das Schiff ist, gemessen in seinen Schritten. Während das Schiff langsam vorwärts fährt, schreitet er dazu am Ufer mit gleichmäßigen Schritten vom Heck des Schiffes zum Bug, wobei er 240 Schritte zählt. Am Bug angekommen dreht er sofort um und schreitet wieder zum Heck des Dampfschiffes zurück, wobei er nun 60 Schritte zählt. Wie lang ist das alte Dampfschiff in Simons Schritten?
96
25 J / 15 S
Die Zahl 137641=371^2 ist die kleinste sechsstellige Zahl, bei der es möglich ist drei paarweise verschiedene Ziffern herauszustreichen, sodass man die Quadratwurzel der gegebenen Zahl erhält: \cancel{1}37\cancel{6}\cancel{4}1. Finde die größte sechsstellige Zahl mit dieser Eigenschaft!
992016 = 996^2
26 J / 16 S
Linda tippt auf ihrem Taschenrechner. Eine dreistellige Zahl erscheint auf dem Display. Patrick, der gegenüber Linda sitzt, sieht aus seiner Sicht auch eine dreistellige Zahl (auf dem Kopf gestellt). Er merkt, dass die Zahl, die er sieht, um 369 größer ist als die eingetippte Zahl. Wie lautet die von Linda eingetippte Zahl?
Hinweis: Der Taschenrechner hat eine Sieben-Segment-Anzeige. Die Ziffern sehen daher so aus:

596
27 J / 17 S
Es leben drei Familien auf der Insel Na-boi. Jede Familie hat zwei Söhne und zwei Töchter. Wie viele Möglichkeiten gibt es, aus diesen zwölf Personen sechs Ehepaare zu bilden, falls Hochzeiten zwischen Geschwistern verboten sind?
80
28 J / 18 S
Hänsel und Gretel haben eine riesengroße, kreisrunde Pizza gebacken. Sie haben 50 gleich große, vom Mittelpunkt ausgehende sektorenförmige Stücke markiert und auf diese in folgender Weise Oliven darauf verteilt: Beginnend bei einem Stück haben sie die nachfolgenden Stücke im Uhrzeigersinn jeweils mit 1, 2, …, 49 und 50 Oliven belegt. Nun wollen sie diese Riesenpizza entlang der Markierungen mit einem geraden Schnitt durch die Mitte so in zwei gleich große Hälften teilen, dass Hänsel zweimal so viele Oliven erhält wie Gretel. Bestimme die Gesamtzahl der Oliven auf den vier Pizzastücken, die direkt an der Schnittkante liegen.
68, 136
29 J / 19 S
Man bestimme alle Primzahlen p mit der Eigenschaft, dass 19p + 1 eine Kubikzahl ist.
421
30 J / 20 S
Im Parallelogramm ABCD liegt der Punkt E auf der Seite AD mit 2\cdot\overline{AE} = \overline{ED} und der Punkt F auf der Seite AB mit 2\cdot \overline{AF} = \overline{FB}. Die Strecken CF und CE schneiden die Diagonale BD in G bzw. H. Welcher Anteil der Fläche des Parallelogramms ABCD wird von der Fläche des Fünfecks AFGHE bedeckt?
\frac{7}{30}
31 J / 21 S
Suche die größte fünfstellige Zahl, die die Ziffer Null nicht enthält, mit folgenden Eigenschaften:
- Die Zahl, die aus den ersten drei Stellen gebildet wird, ist neunmal so groß wie die aus den letzten beiden Stellen gebildete Zahl.
- Die Zahl, die aus den letzten drei Stellen gebildet wird, ist siebenmal so groß wie die aus den ersten beiden Stellen gebildete Zahl.
85595
32 J / 22 S
Zwölf Karten – neun Blankokarten und drei Spezialkarten mit den Symbolen B, D und K – wurden gemischt und verdeckt gleichmäßig an zwölf Schlauberger verteilt, die in einem Kreis saßen. Nachdem jeder von ihnen seine Karte angeschaut hatte, wurden alle Personen aufgefordert, gleichzeitig ihre Hand zu heben, falls sie wissen, wer zu diesem Zeitpunkt welche Spezialkarte in seiner Hand hält. Dann gaben sie ihre Karte an ihren rechten Nachbarn weiter, schauten wieder ihre Karte an, ihnen wurde wieder die selbe Frage gestellt und dieser Ablauf ging so weiter. Nach dem Blick auf die vierte Karte hob niemand die Hand. Genau ein Schlauberger gab ein Handzeichen nach fünf gesehenen Karten. Als nächstes hoben x Schlauberger nach sechs gesehenen Karten die Hand und y nach sieben gesehenen Karten. Bestimme das Produkt xy.
42
33 J / 23 S
In einem gleichschenkligen, rechtwinkligen Dreieck mit der Basislänge 1 werden, wie in der Abbildung dargestellt, schrittweise sieben Kreise konstruiert:
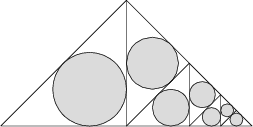
Wie groß ist die Summe der Flächeninhalte aller sieben Kreise?
\pi \frac{3 - 2\sqrt 2}{4} = \pi\frac{(1-\sqrt2)^2}4 = \pi\frac1{4(1+\sqrt2)^2} = \pi\frac1{4(3+2\sqrt2)}
34 J / 24 S
Bestimme alle Primzahlen p, so dass p+11 den Term p(p+1)(p+2) teilt.
7, 11, 19, 79
35 J / 25 S
Kellerasseln (Porcellio scaber) haben 14 Laufbeine. Mutter Kellerassel schaut ihren riesigen Vorrat an identischen Socken und Schuhen durch und bereitet ihre Kinder auf die kommende kalte Jahreszeit vor. Dem kleinen Scaberix erklärt sie, er kann die Socken und Schuhe in beliebiger Reihenfolge anziehen, aber er muss natürlich beim Anziehen eines Schuhes beachten, dass er irgendwann vorher an genau diesen Fuß eine Socke angezogen haben muss. Auf wie viele Arten kann der kleine Scaberix alle seine Füße mit Socken und Schuhen bekleiden?
\frac{28!}{2^{14}}
36 J / 26 S
Es sei x eine reelle Zahl, für welche die Gleichung x^3 + 4x = 8 gilt. Bestimme den Wert von x^7 + 64x^2.
128
37 J / 27 S
Gegeben ist ein gleichschenkliges Dreieck ABC mit der Basis AB. Es sei D der Schnittpunkt der Winkelhalbierenden (Winkelsymmetrale) des Winkels \angle ACB mit der Strecke AB und E der Schnittpunkt der Winkelhalbierenden des Winkels \angle BAC mit der Strecke BC. Weiter ist bekannt, dass \overline{AE} = 2\cdot \overline{CD} ist. Wie groß ist der Winkel \angle BAC ?
36^\circ
38 J / 28 S
Die reelle Zahlenfolge (a_n)_{n\geq 1} sei definiert durch a_1=2015 und die Gleichung für alle n \geq 1. Bestimme a_{2015}.
\frac1{1008}
39 J / 29 S
Katrin und Henriette haben das folgende Spiel erfunden: Sie färben die Seiten von zwei fairen zwölfseitigen Würfeln mit den Farben Türkis, Rosa und Gelb, sodass jede der Farben zumindest einmal auf einer Seite eines jeden Würfels erscheint und die Farbe Gelb auf genau vier Seiten des ersten Würfels vorkommt. Es werden beide Würfel gleichzeitig geworfen. Zeigen beide Würfel dieselbe Farbe, gewinnt Katrin, andernfalls gewinnt Henriette. Die Farben sind so verteilt, dass die Gewinnchance für beide Mädchen gleich ist. Wie viele rosa gefärbte Seiten hat der zweite Würfel?
1, 9
40 J / 30 S
Es sitzen n > 24 Frauen um einen großen runden Tisch. Jede einzelne von diesen lügt immer oder spricht immer die Wahrheit. Jede von ihnen behauptet:
- Ich spreche die Wahrheit.
- Die Person 24 Plätze rechts von mir ist eine Lügnerin.
Finde das kleinste n, für das dies möglich ist.
32
41 J / 31 S
Betrachte zwei Quadrate mit gemeinsamem Zentrum, so dass die Ecken des kleineren Quadrates auf den Seiten des größeren Quadrates liegen. Entfernt man das kleinere Quadrat, so bleiben vier kongruente Dreiecke übrig. Die Fläche eines solchen Dreiecks soll jeweils ein Zwölftel der Fläche des großen Quadrates betragen. Wie groß ist der kleinste Innenwinkel dieser Dreiecke?
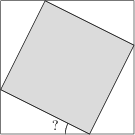
15^\circ
42 J / 32 S
Ein Kreis k_3 mit Radius 3 hat im Inneren zwei Berührkreise k_1 und k_2 mit den zugehörigen Radien 1 und 2. Die Kreise k_1 und k_2 berühren sich zusätzlich von außen. Die Punkte A und B liegen auf k_3 und einer gemeinsamen externen Tangente von k_1 und k_2. Wie lang ist die Strecke AB?
\frac43 \sqrt{14}
43 J / 33 S
Eines Tages traf Ödipus, ein unerschrockener Held, die Sphinx, die ihm folgendes Rätsel aufgab: Nachdem sie eine positive zweistellige Zahl S gewählt hat, darf Ödipus drei einstellige Zahlen a < b < c nennen und fragen, ob S durch diese Zahlen teilbar ist. Für jede dieser Zahlen bekommt er die Antwort ‘ja’ oder ‘nein’. Nachdem er die Antworten bekommen hatte, war Ödipus verzweifelt, denn genau zwei Zahlen erfüllten die genannten Bedingungen. Aber dann teilte ihm die Sphinx mit, dass sie sich bei der Teilbarkeit durch b geirrt hatte. Nun konnte Ödipus die Ausgangszahl eindeutig bestimmen. Wie lautete S?
84
44 J / 34 S
Ein Auto, ein Motorrad, ein Vespa-Roller und ein Fahrrad fuhren eine Straße entlang, jedes Fahrzeug mit einer konstanten Geschwindigkeit. Der Autofahrer holte den Vespa-Roller um 12 Uhr mittags ein und begegnete dem Fahrradfahrer um 14 Uhr sowie dem Motorradfahrer um 16 Uhr. Der Motorradfahrer seinerseits traf den Vespa-Roller um 17 Uhr und holte den Fahrradfahrer um 18 Uhr ein. Wann begegnete der Fahrradfahrer dem Vespa-Roller?
15:20 Uhr
45 J / 35 S
Der Boden einer Halle ist mit einem quadratischen Teppich der Seitenlänge 22 Meter bedeckt. Der Staubsaugerroboter RoboSaug soll den Teppich reinigen. Der Einfachheit halber ist der Teppich in 484 Einheitsquadrate unterteilt und RoboSaug reinigt ein Quadrat nach dem anderen nach folgenden Regeln:
- Wenn ein Einheitsquadrat gesaugt wurde, wird es nicht mehr befahren.
- Der RoboSaug behält eine einmal gewählte Fahrtrichtung bei, bis er sie ändern muss, weil er den Rand oder ein schon gesaugtes Einheitsquadrat erreicht.
- Wenn er die Richtung wechseln muss und es zwei Möglichkeiten gibt, wählt er eine beliebige.
Am Anfang wird der RoboSaug auf ein Einheitsquadrat gesetzt und wählt eine zulässige Startrichtung. Wie viele mögliche Startquadrate gibt es, so dass der RoboSaug den ganzen Teppich saugen kann, wenn er auf einem beliebigen Feld aufhören darf?
20
46 J / 36 S
Die Punkte A, B, C, D, E und F liegen in dieser Reihenfolge im Uhrzeigersinn auf einem Kreis k. Ferner sei AD ein Durchmesser von k und BF schneide die Strecke AD in G und die Gerade CE in H. Außerdem seien \angle FEH = 56^\circ, \angle DGB = 124^\circ und \angle DEC = 34^\circ. Bestimme den Winkel \angle CEB.
22^\circ
47 J / 37 S
Zehn Personen – fünf Frauen und deren Ehemänner – nahmen an n Veranstaltungen teil. Es ist bekannt, dass kein verheiratetes Paar an derselben Veranstaltung teilnahm, jedes nicht verheiratete Paar, auch gleichgeschlechtlich, zusammen genau eine Veranstaltung besuchte und dass eine Person nur an zwei Veranstaltungen anwesend war. Wie lautet das kleinste n, für das dies möglich ist?
14
48 J / 38 S
Sandra und Alex sollen eine dreistellige Zahl \overline{abc}, in der 0 < a < b < c gilt, mit 6 multiplizieren und dann die Zehnerstelle mit der Hunderterstelle vertauschen. Obwohl Alex versehentlich zuerst die Stellen vertauscht und dann multipliziert hat, erhält er das gleiche Ergebnis wie Sandra, die den Anweisungen gefolgt ist. Wie lautet \overline{abc} ?
678
49 J / 39 S
Betrachte ein 5\times 3 – Gitter. Eine Maus in der linken oberen Ecke will ein Stück Käse in der rechten unteren Ecke erreichen, und eine Krabbe in der linken unteren Ecke möchte zur Alge in der rechten oberen Ecke. Die Tiere bewegen sich gleichzeitig, jede Sekunde bewegt sich die Maus ein Feld nach rechts oder unten und die Krabbe bewegt sich ein Feld nach rechts oder oben. Auf wie vielen verschiedenen Wegen können die Tiere ihr Futter erreichen, ohne sich dabei zu treffen?
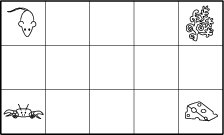
70
50 J / 40 S
Bestimme die Anzahl aller positiven ganzen Zahlen n kleiner gleich 1000, für die \lfloor\sqrt[3]{n}\rfloor ein Teiler von n ist.
Hinweis: Dabei bezeichnet \lfloor x\rfloor den ganzzahligen Anteil einer reellen Zahl x, das heißt die größte ganze Zahl kleiner gleich x.
172
51 J / 41 S
Man bestimme alle reellen Zahlen m, sodass die Lösungen der Gleichung die Längen der Seiten eines rechtwinkligen Dreiecks sind.
281/2
52 J / 42 S
In einem Korb liegen grüne und rote Äpfel, wobei mindestens einer rot ist und mindestens zwei grün sind. Die Wahrscheinlichkeit dafür, dass ein zufällig entnommener Apfel rot ist, ist 42 Mal so groß wie die Wahrscheinlichkeit, dass zwei zufällig (ohne Zurücklegen) entnommene Äpfel beide grün sind. Wie viele grüne und wie viele rote Äpfel befinden sich im Korb?
4 grüne und 21 rote
53 J / 43 S
Gilbert Bates, ein sehr reicher Mann, will sich einen neuen Swimmingpool in seinem Garten bauen lassen. Da er symmetrische Formen sehr gern mag, sagt er seinem Gärtner, dass er einen ellipsenförmigen Pool innerhalb eines Quadrates ABCD der Größe 10\,{\rm m}\times 10\,{\rm m} anlegen soll. Dieser ellipsenförmige Pool soll alle vier Seiten des Quadrates berühren, insbesondere die Seite AB im Punkt P, der genau 2.5\,{\rm m} von A entfernt ist. Der Gärtner, der genau weiß, wie man eine Ellipse konstruieren kann, wenn man die Brennpunkte und einen Punkt auf der Ellipse kennt, überlegt sich, dass er in diesem Fall aufgrund der vorgegebenen Symmetrie nur den Abstand der Brennpunkte benötigt. Kannst Du ihm helfen, den Abstand der Brennpunkte in Metern zu berechnen?
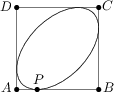
10
54 J / 44 S
Eine Folge (a_n)_{n\geq 1} sei definiert durch a_1=1 und a_n=\lfloor\sqrt{a_1+a_2+\dots+a_{n-1}}\rfloor für n > 1. Bestimme a_{1000}.
Hinweis: Dabei bezeichnet \lfloor x\rfloor den ganzzahligen Anteil einer reellen Zahl x, das heißt die größte ganze Zahl kleiner gleich x.
495
55 J / 45 S
Bestimme die Anzahl von 4 \times 4 –Tabellen mit nicht-negativen, ganzzahligen Einträgen, so dass
- es in jeder Zeile und in jeder Spalte höchstens zwei von Null verschiedene Einträge gibt und
- die Summe der Einträge in jeder Zeile und in jeder Spalte genau 3 ist.
576























