1 J
Petike menő srác az iskolában, így mindig csak felemás színű zoknikat hord. Ruhásszekrénye mélyén összesen 30 darab piros színű, 40 darab zöld színű és 40 darab kék színű zokni található, azonban a szekrény egy sötét padláshelységben helyezkedik el. Petike egyesével veszi ki a zoknikat a szekrényből anélkül, hogy meg tudná állapítani a kivett zokni színét. Legalább hány zoknit kell kivennie ahhoz, hogy biztosan legyen nála 8 pár felemás színű zokni. (Egy zoknit legfeljebb csak egy párba lehet beleszámolni.)
48
2 J
Legyenek x és y pozitív egészek, amelyekre teljesül, hogy x^2 + 2y^2 = 2468. Adjuk meg x-et, hogyha tudjuk, hogy egyetlen megfelelő (x, y) pár létezik. Segítségképpen: 1234 = 28^2 + 2 \cdot 15^2.
30
3 J
Digitális óránk a pontos időt órákban és percekben mutatja a „24 órás” formátumnak megfelelően. Egy nap során hány percben lehet rajta látni az 5-ös számjegyet?
450
4 J
Egy 136\ \text{cm} kerületű nagy téglalap az ábrán látható módon fel lett osztva 7 egybevágó kisebb téglalapra.
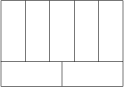
Mekkora a nagy téglalap területe \text{cm}^2-ben mérve?
1120
5 J
Csokoládés dobozunk alakja éppen egy s\ \text{cm} oldalhosszúságú egyenlő oldalú háromszög. Összesen 2n darab egyenlő oldalú háromszög alakú csokoládé van a dobozban, amik együtt kitöltik a rendelkezésre álló helyet: n darab 1\ \text{cm} oldalhosszúságú és n darab 2\ \text{cm} oldalhosszúságú. Mekkora a lehető legkisebb szóba jöhető s értéke?
10
6 J
Petike most már felnőtt, emiatt jelenleg csak egyforma színű zoknikat hajlandó viselni. A nagymamája jóvoltából rengeteg új zoknit is kapott, így immáron 20 barna színű, 30 piros színű, 40 zöld színű, 40 kék színű, 30 fekete színű és 20 fehér színű zokni található a ruhásszekrényében. Azonban a szekrénye továbbra is a sötét padlástérben van. Legalább hány zoknit kell Petikének kivennie ahhoz, hogy biztosan legyen 8 pár páronként egyforma színű zoknija, hogyha továbbra sem látja, hogy milyen színű zoknikat vesz ki? (Egy zoknit legfeljebb csak egy párba lehet beleszámolni.)
21
7 J
Egy négyzet és egy szabályos ötszög ugyanazon köréírt körrel rendelkeznek, továbbá van egy közös csúcsuk is. Mekkora a legnagyobb belső szöge annak a sokszögnek, amely a szóban forgó négyzet és szabályos ötszög metszeteként áll elő?
153^\circ
8 J
Az 1-gyel jelzett kör átmérője 48\ \text{mm}. Mekkora legyen a 2-vel sorszámozott kör átmérője, hogy a berendezés működőképes legyen?
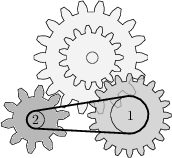
20\ \text{mm}
9 J
A 62 napos júliusi és augusztusi nyári vakációjára Robi pontos tervet készített arról, hogy mely napokon fog hazudni, és mely napokon fog igazat mondani. Valamennyi 1\leq k\leq 62 esetén a vakáció k-adik napján azt mondta, hogy legalább k napon tervezett hazudni. Hányszor hazudott ezen kijelentések során?
31
10 J
A torpedó játékban az ellenfelünk elrejtett egy anyahajót, aminek egy 5 \times 1 vagy 1 \times 5 méretű blokk felel meg valahol a 9 \times 9-es táblán. Legalább hányszor kell lőnünk (tehát kiválasztanunk egy cellát a táblán) ahhoz, hogy biztosan eltaláljuk az anyahajót legalább egyszer?
16
11 J / 1 S
Mi a legnagyobb lehetséges értéke azon a, b és c különböző pozitív egész számok legnagyobb közös osztójának, amelyekre fennáll, hogy a+b+c=2015?
155
12 J / 2 S
Egy vasüzem ellátásáért felelős vonat egy mozdonyból (ami mindig a vonat elején található) és 6 tehervagonból áll, ez utóbbiak mindegyike vagy szenet, vagy vasat tartalmaz rakományként. Ádám le akarta fotózni a vonatot, de nem sikerült a teljes szerelvényt lefényképeznie, csupán egy vasat szállító vagon, és közvetlenül mögötte két szenet szállító vagon látszik a fényképén. A különböző tehervagonok nem teljesen szimmetrikusak, így biztos, hogy a fémet szállító vagon volt a három közül legelöl. Hány féle különböző vonatot lehet lefényképezni úgy, hogy ugyanazt a képet kapjuk, mint amit Ádámnak sikerült?
31
13 J / 3 S
Egy néhány azonos kockából épített tárgy hátulról nézve „1”-esnek néz ki, felülről nézve pedig „3”-asnak (lásd ábra). Hány kocka látható a tárgyban a jobb oldalról nézve, hogyha tudjuk, hogy a lehető legtöbb kockát használtuk fel a tárgy megalkotásához?
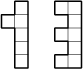
Megjegyzés: A lenti ábrán illusztrációként fel lett tüntetve egy kocka, valamint ugyanezen kocka hátulról, majd felülről nézve.

17
14 J / 4 S
Azt mondjuk, hogy egy n pozitív egész szám finom, hogyha a számjegyeinek összege osztható 17-tel, és ugyanez teljesül (n+10)-re is. Melyik a legkisebb finom szám?
7999
15 J / 5 S
Egy busztársaság az A és D városok között üzemeltet buszjáratokat, a B és C városok érintésével (ebben a sorrendben). A buszjegy ára egyenesen arányos a buszon utazott távolsággal. Például, egy A várostól C városig történő buszozás ugyanannyiba kerül, mint egy A városból B városba, majd egy B városból C városba történő buszozás együttvéve. Továbbá a társaság nem forgalmaz retúrjegyeket, csak vonaljegyeket. Laura szorgalmasan gyűjti a jegyeket, az a célja, hogy minden lehetséges árú jegyet összegyűjtsön az utazás irányától függetlenül. Eddig sikeresen félretett 10, 40, 50, 60 és 70 értékű jegyeket. Mi lehet a hiányzó jegy értéke?
20, 110
16 J / 6 S
Egy óraboltban Hannának szemet szúrt egy karóra, amely egy átlátszó, négyszögletű dobozba van csomagolva úgy, hogy a doboz középpontja és az óra középpontja (a pont, ami körül a mutatók forognak) egybeesik. A doboz rövidebbik oldala 3\ \text{cm} hosszú. Hannának az is feltűnt, hogy délben az óramutató a rövidebbik oldal felezőpontja felé mutat, 1 órakor pedig a doboz sarka felé. Milyen messze van a doboz határán azon pont, amelyre az óramutató 1 órakor mutat, attól a ponttól, amelyre 2 órakor mutat?
\sqrt 3\ \text{cm}
17 J / 7 S
Adjuk meg azt a kilencjegyű számot, amelynek számjegyei az 1,2,\ldots,9 számok egy olyan elrendezésben, hogy bármely két egymást követő számjegyből képzett kétjegyű szám előáll k\cdot l alakú szorzatként, ahol k, l\in\{1,2,\ldots,9\}.
728163549
18 J / 8 S
Határozzuk meg a legnagyobb p prímet, amely kisebb, mint 210 és (210-p) összetett szám!
Megjegyzés: Figyelem! Az 1 se nem prím, se nem összetett.
89
19 J / 9 S
Egy általános iskola vezetősége elhatározta, hogy vesz valamennyi ceruzát és szétosztja az elsős tanulók között, akik három osztályban tanulnak: A, B és C. Hogyha minden tanulónak ugyanannyi ceruzát adnának, akkor mindenki kilencet kapna. Amennyiben minden ceruzát az A osztály tanulói kapnának, úgy minden tanuló ebben az osztályban harminc ceruzához jutna. Amennyiben pedig minden ceruzát a B osztály tanulóinak adnák, úgy minden itt tanuló diák harminchatot tudhatna a magáénak. Hány ceruzát kapna egy C osztályban tanuló diák, hogyha csak a C osztályban tanulók kapnák meg a ceruzákat?
20
20 J / 10 S
Adjuk meg az összes olyan négyjegyű négyzetszámot, amelynek az első két számjegyéből, illetve az utolsó két számjegyéből képzett kétjegyű szám is nemnulla négyzetszám (az utolsó két számjegyből képzett szám első számjegye lehet nulla)!
1681
21 J / 11 S
Egy sofőr a főúton állandó sebességgel szokott haladni két város között. Sajnos a főutat néhány szakaszon éppen javítják, így ezen részeken a sebességét 25%-kal csökkentenie kellett. Emiatt azonban annyi idő alatt, amennyi idő alatt általában megteszi a két város közötti távolságot, most csupán az útnak a hathetedét tudta megtenni. Eddig az időpontig az ideje hanyad részét töltötte a felújítás alatt álló szakaszokon történő áthaladással?
4/7
22 J / 12 S
Egy egész oldalhosszúságú téglalapot felosztottunk 12 négyzetre, melyeknek az oldalai 2, 2, 3, 3, 5, 5, 7, 7, 8, 8, 9 és 9 egység hosszúak. Mekkora a téglalap kerülete?
90
23 J / 13 S
Négyzet alakú papírlapunkat úgy hajtjuk meg, hogy az egyik csúcsa éppen az egyik oldalára essen. Az ábráról leolvasható, hogy keletkezik egy kis háromszög, amely lelóg az eredeti négyzetről. A háromszög azon négyzeten kívül eső oldala, amelyik a hajtáséllel érintkezik, 8\ \text{cm} hosszú, a másik négyzeten kívüli oldala pedig 6\ \text{cm} hosszú.
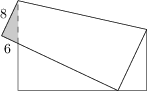
Mekkora oldalhosszúsággal rendelkezik a papírlapunk?
36\ \text{cm}
24 J / 14 S
Egy öreg gőzhajó állandó sebességgel halad egy csatornán. Sanyika meg akarja határozni a hajó hosszát. Mialatt a gőzös lassan halad előre, ő mellette sétál a vízparton a hátuljától egészen az elejéig, szintén állandó sebességgel, s mindeközben összesen 240 lépést tesz meg. Ezután egyből visszafordul, és a hajó orrától egészen a tatjáig sétál ugyanazzal az állandó sebességgel, ezúttal pedig 60 lépést kellett megtennie. Milyen hosszú a hajó lépésekben mérve?
96
25 J / 15 S
137641=371^2 a legkisebb olyan hatjegyű szám, amelyből kihúzható három, páronként különböző számjegy oly módon, hogy megkapjuk a négyzetgyökét: \cancel137\cancel6\cancel41. Határozzuk meg a legnagyobb ilyen tulajdonsággal rendelkező hatjegyű számot!
992016 = 996^2
26 J / 16 S
Lilla beütött valamit a számológépébe, és egy háromjegyű szám jelent meg a kijelzőjén. Patrik, aki vele szemben ült, észrevette, hogy az ő nézőpontjából (tehát fejjel lefelé) egy olyan háromjegyű szám látszik a kijelzőn, amely 369-cel nagyobb a Lilla által beütöttnél. Melyik számot ütötte be Lilla?
Megjegyzés: A számológép az ábrán látható módon képes megjeleníteni a számjegyeket:

596
27 J / 17 S
Na-boi szigetén három család él, mindegyik családnak két fiú és két leány gyermeke van. Hányféleképpen alkothat ezen 12 fiatal hat mátkapárt, hogyha testvérek egymással nem házasodhatnak össze?
80
28 J / 18 S
András és Béla egy hatalmas pizzát sütöttek, amely összesen 50 darab egybevágó, körcikk alakú szeletből áll. A pizzára az olivabogyókat úgy helyezték el, hogy az óramutató járásával megyegyező körüljárással, sorban egymás után 1, 2, 3,\ldots, 50 szem kerüljön az egyes pizzaszeletekre. Szeretnék elfelezni a teljes pizzát egy egyenes vágással a szeletek mentén, de oly módon, hogy András felén kétszer annyi olivabogyó legyen összesen, mint Béláén. Összesen hány olivabogyó található a vágás mentén található négy pizzaszeleten?
68, 136
29 J / 19 S
Határozzuk meg az összes olyan p prímszámot, amelyre 19p + 1 egy egész szám köbe!
421
30 J / 20 S
Az ABCD paralelogrammában tekintsük azt az E pontot, amely az AD oldalon helyezkedik el oly módon, hogy 2\cdot AE = ED, továbbá azt az F pontot, amely az AB oldalon található, és teljesül rá, hogy 2\cdot AF = FB. A CF és CE szakaszok a BD átlót a G és H pontokban metszik. Az így keletkező AFGHE ötszög területe hányad része az ABCD paralelogramma területének?
\frac{7}{30}
31 J / 21 S
Adjuk meg a legnagyobb olyan ötjegyű számot, amely csak nemnulla számjegyeket tartalmaz, és teljesül rá, hogy
- Az első három számjegyéből alkotott szám az utolsó két számjegyéből alkotott számnak éppen a 9-szerese.
- Az utolsó három számjegyéből alkotott szám az első két számjegyéből alkotott számnak éppen a 7-szerese.
85595
32 J / 22 S
Tizenkét okos ember egy kör alakú asztalnál ül. Mindegyikőjük kap egy kártyát véletlenszerűen a tizenkét kártyát tartalmazó paklinkból, amelyben kilenc üres kártyalapon kívül van egy J, egy Q és egy K karakterrel ellátott speciális kártya. Mindegyikőjük megnézi a saját kártyalapját, majd továbbadja azt a jobboldali szomszédjának. Ezt szépen folytatják, mindeközben minden egyes kártyalap megtekintése után egyszerre fel kell emelnie azoknak a kezüket, akik tudják, hogy kinél melyik speciális kártya van az adott pillanatban. Négy kártyalap megtekintése után senki nem emelte fel a kezét. Az ötödik kártya megtekintése után egy ember emelte fel a kezét. Ezután x ember emelte fel a kezét hat kártyalap megtekintése után, majd pedig y ember emelte fel a kezét hét kártyalap megtekintése után. Határozzuk meg xy értékét!
42
33 J / 23 S
Egy egyenlő szárú derékszögű háromszög alapja 1 egység hosszúságú. Eme háromszögben az ábrán látható módon felvettünk hét körlapot:
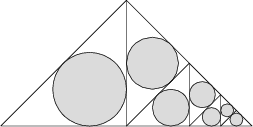
Mekkora a körlapok összterüete?
\pi \frac{3 - 2\sqrt 2}{4} = \pi\frac{(1-\sqrt2)^2}4 = \pi\frac1{4(1+\sqrt2)^2} = \pi\frac1{4(3+2\sqrt2)}
34 J / 24 S
Adjuk meg az összes olyan p prímszámot, amelyre (p+11) osztója a p(p+1)(p+2) számnak!
7, 11, 19, 79
35 J / 25 S
Az ászkarákoknak tizennégy lábuk van összesen. Ászkarákmamának rengeteg egyforma zoknija és cipője van a gyermekei számára a közelgő hideg télre való tekintettel. Jancsi fiának kikötötte, hogy a zoknikat és a cipőket tetszőleges sorrendben húzhatja fel a lábaira, azonban minden egyes lábára előbb egy zoknit kell felhúznia, s csak utána vehet rá egy cipőt. Hányféleképpen öltözhet fel a kis Jancsika, hogyha minden lábára kell, hogy kerüljön zokni és cipő is?
\frac{28!}{2^{14}}
36 J / 26 S
Legyen x egy valós szám, amelyre teljesül, hogy x^3 + 4x = 8. Határozzuk meg x^7 + 64x^2 értékét!
128
37 J / 27 S
Az egyenlő szárú ABC háromszög alapja legyen AB. Legyen D az \angle ACB szög szögfelezőjének és az AB oldalnak a metszéspontja, továbbá legyen E a \angle BAC szög szögfelezőjének és a BC oldalnak a metszéspontja. Határozzuk meg a BAC\sphericalangle szög értékét, hogyha tudjuk, hogy AE = 2\cdot CD!
36^\circ
38 J / 28 S
Legyen (a_n) valós számokból álló sorozat, amelyre a_1=2015, továbbá a_1+a_2+\dots+a_n=n^2\cdot a_n minden n \geq 1 esetén. Határozzuk meg a_{2015} értékét!
\frac1{1008}
39 J / 29 S
Anna és Bea a következő játékot találták ki: két egyforma, tizenkét oldalú szabályos dobókocka oldalait ciánkék, magenta és sárga színekre festették oly módon, hogy mindhárom szín jelen van mindkét dobókockának legalább az egyik oldalán, továbbá az első dobókockán pontosan négy darab sárga színű oldal található. Hogyha ezen két dobókockát eldobva ugyanaz a szín látható legfelül rajtuk, akkor Anna nyer, különben pedig Bea. Tegyük fel, hogy a színek úgy vannak elosztva a dobókockákon, hogy a két lány egyenlő esélyekkel rendelkezik. Hány darab magenta színű oldallapja van a második dobókockának?
1, 9
40 J / 30 S
Egy nagy kerek asztal körül n > 24 asszony ül, mindegyikőjük vagy mindig igazat mond, vagy mindig hazudik. Mindegyik asszony a következőket állítja:
- Ő maga igazat mond.
- A tőle 24 hellyel jobbra található asszony hazudik.
Mekkora a legkisebb n, amely esetében ez megvalósítható?
32
41 J / 31 S
Két négyzet közös középponttal rendelkezik, valamint a kisebbik négyzet csúcsai a nagyobbik oldalain találhatóak. Hogyha a kisebbik négyzetet elhagyjuk a nagyobbikból, akkor négy darab egymással egybevágó háromszög marad hátra, továbbá minden egyes hátramaradt háromszög területe a nagy négyzet területének egy tizenketted része. Mekkora fokokban mérve a legkisebb belső szöge egy ilyen hátramaradt háromszögnek?
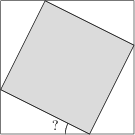
15^\circ
42 J / 32 S
Az \omega_3 kör sugara 3 egység, ezen kört belülről érintik az \omega_1 és \omega_2 körök, melyeknek a sugara 1, illetve 2 egység. Emellett az \omega_1 és \omega_2 egymást kívülről érintik. Az \omega_3-on található A és B pontokat úgy választjuk meg, hogy az AB szakasz egy közös külső érintője legyen az \omega_1 és \omega_2 köröknek. Mekkora az AB szakasz hossza?
\frac43 \sqrt{14}
43 J / 33 S
Oidipusz, a rettenthetetlen hős, egy napon összetalálkozott a mágikus szfinxszel, aki az alábbi rejtvényt adta fel neki: a szfinx választott egy kétjegyű egész S számot. Oidipusz választhatott három darab egyjegyű egész számot, a < b < c-t és megkérdezhette, hogy az S szám osztható-e velük. Minden egyes választott szám esetében kapott egy igen-nem választ a kérdésére. Ezek után Oidipusz kétségbe esett, mivel pontosan két megfelelő szám létezett az általa kiderített oszthatóságok alapján. Szerencsére a szfinx rájött, hogy hibázott, és téves választ adott neki a b számmal való oszthatósággal kapcsolatban. Így már Oidipusz egyértelműen meg tudta határozni a keresett számot. Mi volt ez a S szám?
84
44 J / 34 S
Négy ember halad az utcán, mindegyikőjük állandó sebességgel. Az első autót vezet, a második motorkerékpárral utazik, a harmadik egy kis robogóval közlekedik, a negyedik pedig biciklit teker. Az autós délben, 12 órakor találkozott a robogóval, délután 2-kor a biciklissel és délután 4-kor a motorkerékpárossal. A motorkerékpáros délután 5-kor talákozott a robogóssal és délután 6-kor a kerékpározó személlyel. Mikor találkozott a bicikli és a robogó?
Délután 3 óra 20 perc
45 J / 35 S
Lakosztályunk padlóján egy négyzet alakú szőnyeg van kiterítve, amelynek oldalai huszonkét méter hosszúak. Egy automata porszívó azt a feladatot kapta, hogy porszívózza ki a szőnyeget. A könnyebbség kedvéért a szőnyeg fel van osztva 484 darab egységnyi négyzetre. Az automata porszívó egységenként takarít az alábbi szabályoknak megfelelően:
- Ha végzett egy egység kitakarításával, arra újfent már nem mehet rá.
- Egy irányba halad mindaddig, amíg el nem ér a szőnyeg széléig, vagy egy már korábban kitakarított egységig.
- Hogyha irányt kell váltania, és két lehetséges opció is a rendelkezésére áll, azt választja, amelyiket szeretné.
Kezdetben az automatát elhelyezzük egy egységen, ahonnan a rendelkezésre álló irányok bármelyikébe folytathatja a munkáját. Hány darab egység van a szőnyegen, amelyről indulva be tudja fejezni a teljes szőnyeg takarítását, hogyha nem szükséges, hogy a szőnyeg szélén végezzen?
20
46 J / 36 S
Vegyük fel az óramutató járásával megegyezően sorban az A, B, C, D, E és F pontokat az \omega körön. Tegyük fel, hogy AD az \omega egy átmérője, BF pedig messe az AD és CE szakaszokat a G és H pontokban. Legyenek továbbá FEH\sphericalangle = 56^\circ, DGB\sphericalangle = 124^\circ és DEC\sphericalangle = 34^\circ. Mekkora a \angle CEB szög?
22^\circ
47 J / 37 S
Tíz felnőtt – öt feleség, és a férjeik – részt vett összesen E eseményen. Tudjuk, hogy egy házaspár sem vett részt ugyanazon az eseményen. Azt is tudjuk, hogy minden lehetséges nem házas pár (azonos nemű párokat is beleértve) részt vett közösen pontosan egy eseményen, valamint, hogy pontosan egy személy volt pontosan két esemény résztvevője. Mekkora az E lehetséges legkisebb értéke?
14
48 J / 38 S
Az iskolában Daniék a következő feladatot kapták: a tanárnő adott nekik egy háromjegyű \overline{abc} számot, amelyre teljesült, hogy 0 < a < b < c. A feladatuk az volt, hogy szorozzák meg 6-tal, majd cseréljék fel a tízesek és a százasok helyiértékén álló számjegyet. Dani tévedésből a 6-tal való szorzás előtt cserélte fel a számjegyeket, de az eredménye így is helyes lett. Határozzuk meg \overline{abc}-t!
678
49 J / 39 S
Tekintsünk egy 5 \times 3-as rácsot. A rács bal felső sarkában ül egy kisegér, aki el akar jutni a jobb alsó sarokban található sajthoz. Emellett a rács bal alsó sarkában ül egy rákocska, aki pedig a jobb felső sarokban található algalevelet szemelte ki magának. A két állat egyszerre mozog a rácson. Minden másodpercben az egér egy rácsnyit halad jobbra vagy lefelé, a rák pedig egy rácsnyit halad jobbra vagy felfelé. Hányféleképpen érhetik el a céljukat úgy, hogy útközben ne találkozzanak?
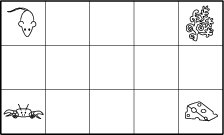
70
50 J / 40 S
Adjuk meg azon 1000-nél nem nagyobb n pozitív egész számok számát, amelyekre \lfloor\sqrt[3]{n}\rfloor az n egy osztója.
Megjegyzés: A \lfloor x\rfloor kifejezés az x egészrészét jelenti, azaz a legnagyobb olyan egész számot, amely nem nagyobb, mint x.
172
51 J / 41 S
Adjuk meg az összes olyan valós m számot, amelyre az alábbi egyenlet gyökei egy derékszögű háromszög oldalhosszainak feleltethetőek meg:
281/2
52 J / 42 S
Egy kosárban zöld és piros almák találhatóak, legalább egy darab piros, és legalább két darab zöld alma van benne. Annak a valószínűsége, hogy egy véletlenszerűen kiválasztott alma piros negyvenkétszer akkora, mint annak a valószínűsége, hogy két véletlenszerűen (visszatevés nélkül) kiválasztott alma közül mindkettő zöld. Hány zöld és hány piros alma van a kosárban?
4 zöld és 21 piros
53 J / 43 S
Pénzes Pál, egy nagyon gazdag úriember, új úszómedencét szeretne a kertjében. Szereti a szimmetrikus dolgokat, így a kertészének azt parancsolta, hogy egy ellipszis alakú medencét hozzon neki létre egy 10\ \text{m}\times 10\ \text{m}-es ABCD négyzet alakú területen belül. A medencének mind a négy négyzetoldalt érintenie kell, ráadásul az AB oldalt az A csúcstól 2,5\ \text{m}-re elhelyezkedő P pontban. A kertész pontosan tudja, hogyan ássa ki az ellipszis alakú medencének a helyet, hogyha adva vannak az ellipszis fókuszpontjai, valamint egy pont az ellipszisen. Megállapította, hogy a szimmetrikus elrendezés miatt csupán a fókuszpontok közötti távolságra van szüksége. Segítsünk a kertésznek azzal, hogy meghatározzuk méterben mérve a kívánt távolságot!
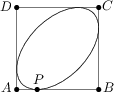
10
54 J / 44 S
Az (a_n) sorozatot a következőképpen definiáljuk. Legyen a_1=1, továbbá minden n > 1 esetében. Határozzuk meg a_{1000} értékét!
Megjegyzés: Az \lfloor x\rfloor kifejezés az x egészrészét jelenti, azaz a legnagyobb olyan egész számot, amely nem nagyobb, mint x.
495
55 J / 45 S
Határozzuk meg azon 4 \times 4-es nemnegatív egész számokat taralmazó táblázatok számát, amelyekre teljesül, hogy
- minden sorban és minden oszlopban legfeljebb két nemnulla szám található,
- minden sorban és minden oszlopban az ott található számok összege 3.
576