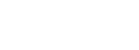1 J
Mały Karol jest ekscentrykiem, który nosi tylko pary skarpetek w różnych kolorach. W jego szafie znajdującej się w głębi ciemnej piwnicy jest 30 czerwonych, 40 zielonych i 40 niebieskich skarpetek. Karol wyciąga z szafy skarpetki jedną po drugiej, nie mogąc jednak rozpoznać koloru żadnej z nich. Jaka jest najmniejsza liczba skarpetek, które musi wyjąć z szafy, jeżeli chce mieć pewność uzyskania ośmiu dwukolorowych par skarpetek? Żadna skarpetka nie może być policzona w dwóch różnych parach.
48
2 J
Przypuśćmy, że x i y to dodatnie liczby całkowite spełniające x^2+2y^2=2468. Znajdź x, jeżeli wiadomo, że istnieje dokładnie jedna taka para (x,y) oraz 1234=28^2+2\cdot 15^2.
30
3 J
Cyfrowy zegar wyświetla czas (godziny i minuty) w formacie dwudziestoczterogodzinnym. Przez ile minut w ciągu doby na wyświetlaczu zegara widoczna jest cyfra 5?
450
4 J
Duży prostokąt o obwodzie 136\ \text{cm} jest podzielony na siedem przystających prostokątów, jak na rysunku.
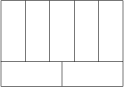
Jakie jest pole dużego prostokąta w \text{cm}^2?
1120
5 J
Pudełko czekoladek ma kształt trójkąta równobocznego o boku s\ \text{cm}. Pudełko jest szczelnie wypełnione przez 2n czekoladek, z których n jest w kształcie trójkąta równobocznego o boku 1\ \text{cm}, a n — trójkąta równobocznego o boku 2\ \text{cm}. Jaka jest najmniejsza możliwa wartość s?
10
6 J
Mały Karol wyrósł już ze swego ekscentryzmu i teraz nosi tylko pary skarpetek w tym samym kolorze. Ma też sporo nowych skarpetek, w jego szafie znajduje się teraz 20 brązowych, 30 czerwonych, 40 zielonych, 40 niebieskich, 30 czarnych i 20 białych skarpetek. Szafa jest jednak wciąż zlokalizowana w nieoświetlonej piwnicy. Jaka jest najmniejsza liczba skarpetek, które Karol musi wyjąć z szafy, aby mieć pewność uzyskania ośmiu par? Żadna skarpetka nie może być policzona w dwóch różnych parach.
21
7 J
Kwadrat i pięciokąt foremny są wpisane w ten sam okrąg i mają wspólny wierzchołek. Ile wynosi miara największego z kątów wewnętrznych wielokąta będącego częścią wspólną kwadratu i pięciokąta?
153^\circ
8 J
Koło numer 1 ma średnicę 48\ \text{mm}. Jaką średnicę powinno mieć koło numer 2, aby cały mechanizm działał poprawnie?
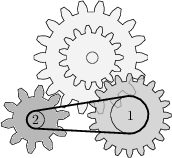
20\ \text{mm}
9 J
Na swoje 62-dniowe letnie wakacje w lipcu i sierpniu Włodek przygotował dokładny plan, w które dni będzie kłamał, a w które mówił prawdę. Następnie, Włodek k-tego dnia wakacji (dla każdego k od 1 do 62) stwierdzał, że zaplanował kłamanie w co najmniej k dni. Jak wiele spośród tych stwierdzeń było kłamstwami?
31
10 J
W grze w statki, która toczy się na planszy o wymiarach 9 \times 9, nasz przeciwnik gdzieś ukrył lotniskowiec, reprezentowany przez prostokąt o wymiarach 5 \times 1 lub 1 \times 5. Jaka jest minimalna liczba strzałów, które musimy oddać, by choć raz trafić lotniskowiec, niezależnie od jego lokalizacji?
16
11 J / 1 S
Jaka jest największa możliwa wartość wspólnego dzielnika różnych dodatnich liczb całkowitych a, b, c spełniających równość a+b+c=2015?
155
12 J / 2 S
Pociąg towarowy składa się z lokomotywy (która zawsze jest na początku) oraz sześciu wagonów, z których każdy przewozi węgiel lub rudę żelaza. Ada próbowała zrobić zdjęcie pociągu, ale w kadrze zmieścił się tylko jeden wagon z rudą żelaza oraz dwa wagony z węglem znajdujące się bezpośrednio za nim. Wagony były wystarczająco niesymetryczne i dla Ady jasne było, gdzie jest przód wagonu, a gdzie tył. Jak wiele różnych pociągów można sfotografować tak, by otrzymać takie samo zdjęcie, jak zdjęcie Ady?
31
13 J / 3 S
Bryła zbudowana z pewnej liczby identycznych sześcianów wygląda jak „1” od tyłu i jak „3” od góry (rysunek). Ile sześcianów można ujrzeć patrząc na tę bryłę od prawej strony, jeżeli wiadomo, że składa się ona z największej możliwej liczby sześcianów?
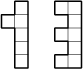
Uwaga: Poniższy rysunek przedstawia sześcian oraz odpowiednio widok tego sześcianu od tyłu i od góry.

17
14 J / 4 S
Powiemy, że dodatnia liczba całkowita n jest nábojowa, jeżeli suma cyfr tej liczby jest podzielna przez 17 oraz suma cyfr liczby n+10 także jest podzielna przez 17. Jaka jest najmniejsza liczba nábojowa?
7999
15 J / 5 S
Przedsiębiorstwo autobusowe obsługuje linię między miastami A i D z przystankami w miastach B i C (w tej właśnie kolejności). Cena biletu jest wprost proporcjonalna do odległości przemierzanej przez autobus na danej trasie. Na przykład bilet z A do C kosztuje tyle samo, co łącznie bilety z A do B oraz z B do C. W ofercie nie ma jednak biletów powrotnych, są tylko bilety w jedną stronę. Dominik, zapalony kolekcjoner biletów autobusowych, chciałby zebrać bilety o wszystkich możliwych cenach, bez względu na kierunek podróży. Jak dotąd ma w swojej kolekcji bilety kosztujące 10, 40, 50, 60 i 70. Jakie są możliwe ceny brakującego biletu?
20, 110
16 J / 6 S
Podczas zakupów, Sławek zwrócił uwagę na zegarek, który jest zapakowany w przezroczyste prostokątne opakowanie. Zegarek jest tak ułożony, że środek pudełka oraz środek zegarka (tzn. punkt wspólny jego wskazówek) się pokrywają. Krótszy bok opakowania ma długość 3\ \text{cm}. Sławek zauważył, że w południe wskazówka zegarowa wskazuje środek krótszego boku pudełka, a o godzinie pierwszej — róg pudełka. Jak daleko od siebie znajdują się punkty na brzegu opakowania, które są wskazywane przez wskazówkę godzinową o godzinach odpowiednio pierwszej i drugiej?
\sqrt 3\ \text{cm}
17 J / 7 S
Znajdź dziewięciocyfrową liczbę składającą się z cyfr 1,2,\ldots,9 ustawionych w pewnej kolejności, o tej własności, że jej każde dwie kolejne cyfry tworzą liczbę dwucyfrową, którą można przedstawić w postaci iloczynu k\cdot l, gdzie k, l\in\{1,2,\ldots,9\}.
728163549
18 J / 8 S
Znajdź największą liczbę pierwszą p mniejszą od 210 o tej własności, że liczba 210-p jest złożona. Uwaga: Liczba 1 nie jest ani pierwsza, ani złożona.
89
19 J / 9 S
Rada rodziców III LO w Krakowie postanowiła kupić pewną liczbę ołówków i rozdać je uczniom pierwszych klas. W szkole są trzy oddziały klas pierwszych: Ia, Ib i Ic. Wiadomo, że gdyby ołówki zostały rozdane po równo wszystkim uczniom, każdy otrzymałby po 9 ołówków. Gdyby zostały rozdane po równo uczniom klasy Ia, każdy uczeń tej klasy dostałby po 30 ołówków. Jeśli zostałyby rozdane tylko uczniom klasy Ib, każdy z nich otrzymałby po 36 ołówków. Po ile ołówków dostałby każdy uczeń klasy Ic, gdyby postanowiono je rozdać uczniom tylko tej klasy?
20
20 J / 10 S
Znajdź wszystkie czterocyfrowe kwadraty liczb naturalnych, których zarówno pierwsze dwie cyfry, jak i ostatnie dwie, tworzą liczby będące kwadratami dodatnich liczb całkowitych (druga liczba może rozpoczynać się zerem).
1681
21 J / 11 S
Kierowca ciężarówki zwykle pokonuje dystans między dwoma miastami jadąc autostradą ze stałą prędkością. Niestety, podczas ostatniego przejazdu na niektórych odcinkach autostrady trwał remont, w wyniku czego kierowca musiał podczas jazdy na tych odcinkach zredukować prędkość o jedną czwartą. W wyniku tego w czasie, w którym zwykle pokonałby całą trasę, udało mu się przebyć tylko sześć siódmych jej długości. Jaką część czasu poświęconego na przebycie tej drogi kierowca jechał przez remontowane odcinki?
4/7
22 J / 12 S
Prostokąt o wymiarach całkowitych został rozcięty na dwanaście kwadratów o następujących długościach boków: 2, 2, 3, 3, 5, 5, 7, 7, 8, 8, 9, 9. Ile wynosi obwód wyjściowego prostokąta?
90
23 J / 13 S
Kwadratowa kartka papieru jest zagięta w taki sposób, że jeden z jej wierzchołków leży dokładnie na jednej z krawędzi kartki. Jak pokazano na rysunku, pewien trójkąt wychodzi poza wyjściowy kwadrat. Długość boku tego trójkąta przyległego do linii zgięcia wynosi 8\ \text{cm}, a długość boku przyległego do boku kwadratu jest równa 6\ \text{cm}.
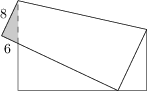
Jaka jest długość boku kartki?
36\ \text{cm}
24 J / 14 S
Statek parowy przepływa przez kanał ze stałą prędkością. Maciek chciałby zmierzyć jego długość. Podczas gdy statek powoli sunie do przodu, chłopiec idzie brzegiem kanału ze stałą prędkością, przechodząc od rufy do dziobu w 240 krokach. Następnie odwraca się i zaczyna iść z powrotem w kierunku rufy, osiągając ją po 60 krokach. Jaka jest długość statku parowego w krokach?
96
25 J / 15 S
Liczba 137641=371^2 to najmniejsza liczba sześciocyfrowa o tej własności, że wykreślając z niej trzy parami różne cyfry można otrzymać pierwiastek kwadratowy z tej liczby: \cancel137\cancel6\cancel41. Znajdź największą liczbę sześciocyfrową o tej własności.
992016 = 996^2
26 J / 16 S
Teodor wpisał na klawiaturze kalkulatora pewną trzycyfrową liczbę. Michał, który siedział naprzeciwko, zauważył, że gdy się popatrzy na wyświetlacz do góry nogami, można odczytać liczbę, która jest większa o 369 od tej faktycznie wpisanej. Jaką liczbę wpisał Teodor? Uwaga: Kalkulator ma standardowy elektroniczny wyświetlacz, cyfry wyglądają tak jak na rysunku poniżej:

596
27 J / 17 S
Na wyspie Na-boi żyją trzy rodziny. Do każdej z nich należy dwóch synów i dwie córki. Na ile sposobów można zaaranżować sześć heteroseksualnych małżeństw pomiędzy tymi osobami, zakładając, że małżeństwa pomiędzy rodzeństwem są zabronione?
80
28 J / 18 S
Jacek i Marta upiekli bardzo dużą pizzę składającą się z 50 jednakowych kawałków w kształcie wycinka koła. Na pizzy rozłożyli oliwki w taki sposób, że liczby oliwek na kolejnych kawałkach zgodnie z ruchem wskazówek zegara to 1,2,3,\ldots,50. Teraz chcą podzielić pizzę na dwie równe połówki jednym prostym cięciem pomiędzy kawałkami w taki sposób, aby na połówce Jacka znalazło się dwa razy więcej oliwek niż na połówce Marty. Znajdź łączną liczbę oliwek znajdujących się na czterech kawałkach przyległych do linii cięcia.
68, 136
29 J / 19 S
Znajdź wszystkie liczby pierwsze p o tej własności, że liczba 19p+1 jest sześcianem pewnej liczby całkowitej.
421
30 J / 20 S
Na boku AD równoległoboku ABCD wybrano taki punkt E, że 2\cdot AE = ED, a na boku AB wybrano taki punkt F, że 2\cdot AF = FB. Proste CF i CE przecinają przekątną BD odpowiednio w punktach G i H. Jaką część powierzchni równoległoboku ABCD zajmuje pięciokąt AFGHE?
\frac{7}{30}
31 J / 21 S
Znajdź największą liczbę pięciocyfrową składającą się z niezerowych cyfr, która ma poniższe własności:
- pierwsze trzy cyfry tworzą liczbę, która jest 9 razy większa od liczby utworzonej przez dwie ostatnie cyfry,
- trzy ostatnie cyfry tworzą liczbę, która jest 7 razy większa od liczby utworzonej przez pierwsze dwie cyfry.
85595
32 J / 22 S
Każdy z dwunastu bystrych studentów siedzących w kółku otrzymał jedną kartę losowo wybraną z dwunastu, wśród których było 9 kart pustych oraz trzy specjalne, oznaczone J, Q, K. Każdy spojrzał na swoją kartę, a następnie podał ją swojemu sąsiadowi siedzącemu z prawej strony. Proces ten był kontynuowany i po każdym spojrzeniu w karty wszyscy byli jednocześnie proszeni o podniesienie ręki jeśli są w stanie bez wątpienia stwierdzić, kto trzyma którą z kart specjalnych w danym momencie. Nikt nie podniósł ręki po obejrzeniu czterech kart. Dokładnie jeden student podniósł rękę po obejrzeniu swojej piątej karty. Następnie x innych studentów podniosło ręce po zobaczeniu szóstej karty, a y — po zobaczeniu siódmej. Znajdź iloczyn xy.
42
33 J / 23 S
Wewnątrz równoramiennego trójkąta prostokątnego o przeciwprostokątnej długości 1 znajduje się siedem kół, jak pokazano na rysunku poniżej:
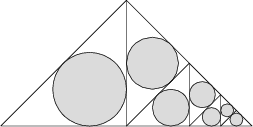
Jakie jest łączne pole wszystkich kół?
\pi \frac{3 - 2\sqrt 2}{4} = \pi\frac{(1-\sqrt2)^2}4 = \pi\frac1{4(1+\sqrt2)^2} = \pi\frac1{4(3+2\sqrt2)}
34 J / 24 S
Znajdź wszystkie liczby pierwsze p o tej własności, że liczba p+11 jest dzielnikiem liczby p(p+1)(p+2).
7, 11, 19, 79
35 J / 25 S
Prosionek piwniczny (Porcellio scaber) to gatunek stonogi mającej czternaście nóżek. Mama stonoga ma dużo identycznych skarpetek i butów, które przygotowała dla swoich dzieci na nadchodzącą zimę. Wyjaśniła małemu prosionkowi Łukaszowi, że może założyć swoje skarpetki i buty w dowolnej kolejności, ale musi pamiętać, by na każdą nogę z osobna najpierw założyć skarpetkę, a dopiero potem buta. Na ile sposobów mały Łukasz może ubrać wszystkie swoje nóżki?
\frac{28!}{2^{14}}
36 J / 26 S
Niech x będzie liczbą rzeczywistą spełniającą równanie x^3+4x=8. Znajdź wartość wyrażenia x^7+64x^2.
128
37 J / 27 S
W trójkącie równoramiennym ABC o podstawie AB dwusieczna kąta ACB przecina prostą AB w punkcie D, a dwusieczna kąta BAC przecina prostą BC w punkcie E. Wyznacz \angle BAC, jeśli wiadomo, że AE=2\cdot CD.
36^\circ
38 J / 28 S
Dany jest ciąg liczb rzeczywistych (a_n), w którym a_1=2015 oraz a_1+a_2+\dots+a_n=n^2\cdot a_n dla każdego n \geq 1. Znajdź a_{2015}.
\frac1{1008}
39 J / 29 S
Kasia i Ania wymyśliły następującą grę: Pokolorowały każdą ze ścian dwóch symetrycznych dwunastościennych kostek na czerwono, zielono lub niebiesko w taki sposób, aby każdy z kolorów pojawił się na każdej z kostek co najmniej raz oraz aby w sumie były dokładnie cztery niebieskie ściany na pierwszej kostce. Jeżeli po rzucie tak przygotowanymi kośćmi na obu wypadnie ściana tego samego koloru, wygrywa Kasia, w przeciwnym wypadku wygrywa Ania. Załóżmy, że kolory ścian są tak dobrane, aby każda z dziewczynek miała jednakową szansę na zwycięstwo. Ile ścian koloru zielonego znajduje się na drugiej kostce?
1, 9
40 J / 30 S
Przy dużym okrągłym stole siedzi n>24 polityków, z których każdy albo zawsze kłamie, albo zawsze mówi prawdę. Każdy z nich twierdzi, że
- sam jest prawdomówny,
- polityk siedzący dwadzieścia cztery miejsca dalej na prawo jest kłamcą.
Wyznacz najmniejszą liczbę naturalną n, dla której taka sytuacja jest możliwa.
32
41 J / 31 S
Dwa kwadraty mają wspólny środek, a wierzchołki mniejszego z nich należą do boków większego. Jeżeli wytniemy z większego kwadratu mniejszy, pozostaną cztery przystające trójkąty, z których każdy ma pole równe 1/12 pola większego kwadratu. Jaką miarę ma najmniejszy z kątów wewnętrznych w każdym z otrzymanych czterech trójkątów?
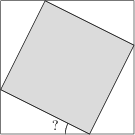
15^\circ
42 J / 32 S
Okrąg \omega_3 o promieniu 3 jest styczny wewnętrznie do okręgów \omega_1 i \omega_2 o promieniach odpowiednio 1 i 2. Co więcej, okręgi \omega_1 i \omega_2 są styczne zewnętrznie. Na okręgu \omega_3 wybrano punkty A, B w taki sposób, że prosta AB jest wspólną styczną zewnętrzną okręgów \omega_1 i \omega_2. Znajdź długość odcinka AB.
\frac43 \sqrt{14}
43 J / 33 S
Pewnego dnia nieustraszony Edyp spotkał na swojej drodze Sfinksa, który zadał mu następującą zagadkę. Zadaniem Edypa było zgadnięcie wybranej przez Sfinksa dwucyfrowej liczby dodatniej S. Edyp mógł wybrać trzy jednocyfrowe dodatnie liczby całkowite a<b<c, a następnie zapytać czy S jest przez nie podzielna. Dla każdej z tych liczb, Edyp otrzymał osobną odpowiedź („tak” lub „nie”). Po otrzymaniu odpowiedzi Edyp był zrozpaczony, gdyż istniały dokładnie dwie liczby spełniające kryteria. Wtedy Sfinks przyznał się do pomyłki przy odpowiedzi na pytanie o podzielność przez b. W tej sytuacji Edyp wyznaczył jednoznacznie liczbę S. Jaka była wartość S?
84
44 J / 34 S
Cztery osoby poruszają się wzdłuż prostej drogi, każda ze stałą prędkością. Pierwsza osoba prowadzi samochód, druga porusza się motocyklem, trzecia jedzie skuterem, a czwarta rowerem. Kierowca samochodu spotkał prowadzącego skuter o 12 w południe, rowerzystę o 14, a motocyklistę o 16. Motocyklista spotkał jadącego skuterem o 17, a rowerzystę o 18. O której godzinie nastąpiło spotkanie rowerzysty z kierującym skuterem?
15:20
45 J / 35 S
Na podłodze w auli Collegium Novum UJ znajduje się kwadratowy dywan o boku długości 22 metrów. Robotyczny odkurzacz (robod) otrzymał zadanie wyczyszczenia całego dywanu. Dla wygody dywan jest podzielony na 484 kwadraty jednostkowe, które robod czyści jeden po drugim. Robod postępuje zgodnie z następującymi zasadami:
- Jeżeli pewien kwadrat został już odkurzony, robod nie może wjechać na niego ponownie.
- Robod jedzie cały czas w tym samym kierunku dopóki nie jest zmuszony by zmienić kierunek, gdy natrafi na krawędź dywanu lub już odkurzony kwadrat.
- Gdy robod musi zmienić kierunek ruchu i ma do wyboru dwie opcje, może wybrać tę, którą preferuje.
Na początku robod jest umieszczony w jednym z kwadratów i może wybrać dowolny kierunek. Dla ilu kwadratów startowych robod będzie mógł wyczyścić cały dywan?
20
46 J / 36 S
Punkty A, B, C, D, E, F leżą w tej właśnie kolejności, zgodnie z ruchem wskazówek zegara, na okręgu \omega w taki sposób, że AD jest średnicą okręgu \omega. Prosta BF przecina AD i CE odpowiednio w punktach G i H, przy czym \angle FEH = 56^\circ, \angle DGB = 124^\circ oraz \angle DEC= 34^\circ. Znajdź \angle CEB.
22^\circ
47 J / 37 S
Dziesięć osób — pięć kobiet i ich mężowie — wzięło udział w N imprezach. Wiemy, że żadna para małżonków nie wzięła udziału w tej samej imprezie, a każda para nie-małżonków (włączając pary tej samej płci) wzięła razem udział w dokładnie jednej imprezie. Ponadto jedna z osób była tylko na dwóch imprezach. Jaka jest najmniejsza wartość N, dla której taka sytuacja jest możliwa?
14
48 J / 38 S
Nauczyciel podał uczniom trzycyfrową liczbę \overline{abc}, w której 0 < a < b < c. Zadanie polegało na pomnożeniu tej liczby przez 6, a następnie zamienieniu miejscami cyfry dziesiątek z cyfrą setek. Zaspany Andrzej źle zapamiętał kolejność poleceń i najpierw dokonał zamiany cyfr, a dopiero potem pomnożył przez 6. Wynik okazał się jednak poprawny! Znajdź \overline{abc}.
678
49 J / 39 S
Rozważmy szachownicę 5 \times 3. W rogach szachownicy znajdują się kolejno mysz, krab, ser i algi. Mysz znajdująca się w lewym górnym rogu chce dotrzeć do sera, który znajduje się w prawym dolnym rogu. Zadaniem kraba znajdującego się początkowo w lewym dolnym rogu jest dotarcie do alg, które znajdują się w prawym górnym rogu. Zwierzęta ruszają się jednocześnie, przy czym w każdej sekundzie mysz idzie o jedno pole w dół lub w prawo, zaś krab jedno pole w górę lub w prawo. Na ile sposobów zwierzęta mogą dotrzeć do swoich przysmaków tak, aby nigdy się nie spotkały?
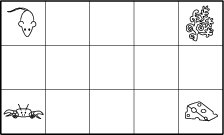
70
50 J / 40 S
Wyznacz liczbę takich dodatnich liczb całkowitych n nie większych od 1000, że liczba \lfloor\sqrt[3]{n}\rfloor jest dzielnikiem liczby n. Uwaga: Symbolem \lfloor x\rfloor oznaczamy część całkowitą liczby x tzn. największą liczbę całkowitą nie większą od x.
172
51 J / 41 S
Wyznacz wszystkie liczby rzeczywiste m, dla których pierwiastki równania są długościami boków trójkąta prostokątnego.
281/2
52 J / 42 S
W pudełku znajdują się jabłka w dwóch różnych kolorach: zielonym i czerwonym. Wiadomo, że przynajmniej jedno jabłko jest czerwone, oraz przynajmniej dwa jabłka są zielone. Prawdopodobieństwo, że losowo wybrane jabłko jest czerwone jest 42 razy większe niż prawdopodobieństwo, że wśród dwóch losowo wybranych jabłek (bez zwracania) oba są zielone. Ile jest zielonych, a ile czerwonych jabłek?
4 zielone i 21 czerwonych
53 J / 43 S
Jasiek Kluczyk, bardzo bogaty człowiek, chce wybudować w swoim ogrodzie basen. Jasiek lubi symetrię, dlatego poprosił ogrodnika o wybudowanie basenu w kształcie elipsy w kwadracie ABCD o wymiarach 10\ \text{m}\times 10\ \text{m} spełniającego szereg wytycznych. Basen musi być styczny do wszystkich boków kwadratu, w szczególności do boku AB w punkcie P, który jest odległy o 2{,}5\ \text{m} od A. Ogrodnik wie jak skonstruować elipsę, mając dane ogniska oraz punkt na elipsie, wie również, że dzięki symetrii potrzebuje znać jedynie odległość między ogniskami. Jednak z tym zadaniem, ogrodnik ma problem i poprosił Ciebie o pomoc. Oblicz odległość między ogniskami.
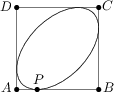
10
54 J / 44 S
Ciąg (a_n) dany jest wzorami a_1=1, oraz a_n=\lfloor\sqrt{a_1+a_2+\dots+a_{n-1}}\rfloor dla n > 1. Wyznacz a_{1000}. Uwaga: Symbolem \lfloor x\rfloor oznaczamy część całkowitą liczby x, tzn. największą liczbę całkowitą nie większą od x.
495
55 J / 45 S
W pola szachownicy 4 \times 4 wpisujemy nieujemne liczby całkowite. Wyznacz liczbę szachownic 4 \times 4 spełniających warunki
- w każdym wierszu i każdej kolumnie co najwyżej dwa pola zawierają liczbę niezerową,
- suma liczb w każdym wierszu i każdej kolumnie wynosi 3.
576