1 J
Malý Peťko kráča s dobou, a preto nosí pár ponožiek tak, že na každej nohe má ponožku inej farby. K dispozícii má 30 červených, 40 zelených a 40 modrých ponožiek vo svojej komode v neosvetlenej izbe. Peťko vyberá z komody postupne po jednej ponožke bez toho, aby sa pozrel na jej farbu, až kým nemá potrebný počet. Aký najmenší počet ponožiek potrebuje vybrať z komody, aby mal určite osem dvojfarebných párov ponožiek?
Poznámka: Ponožka nemôže byť započítaná do dvoch rôznych párov.
48
2 J
Predpokladajme, že x a y sú kladné celé čísla spĺňajúce rovnicu x^2 + 2y^2 = 2468. Určte hodnotu x, ak viete, že existuje len jedna taká dvojica (x, y) a 1234 = 28^2 + 2 \cdot 15^2.
30
3 J
Digitálne hodinky zobrazujú čas v hodinách a minútach použitím 24-hodinového formátu času. Koľko minút za deň je na displeji digitálnych hodiniek možné vidieť číslicu 5?
450
4 J
Veľký obdĺžnik s obvodom 136\ \text{cm} je rozdelený na 7 zhodných obdĺžnikov ako na obrázku.
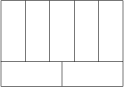
Aký je obsah veľkého obdĺžnika v \text{cm}^2?
1120
5 J
Bonboniéra má tvar rovnostranného trojuholníka so stranou dĺžky s\ \text{cm}. Je v nej 2n čokoládok v tvare rovnostranných trojuholníkov, ktoré bez medzier vypĺňajú bonboniéru: n z nich má stranu dĺžky 1\ \text{cm} a ďalších n čokoládok má stranu dĺžky 2\ \text{cm}. Aká je najmenšia možná hodnota s?
10
6 J
Malý Peťko vyrástol a teraz nosí ponožky tak, že má obe ponožky rovnakej farby. Aktuálne má vo svojej komode 20 hnedých, 30 červených, 40 zelených, 40 modrých, 30 čiernych a 20 bielych ponožiek. Komoda je ale stále umiestnená v neosvetlenej miestnosti. Aký je najmenší počet ponožiek, ktorý musí Peťko vybrať z komody, aby určite mal osem klasických párov ponožiek, ak počas výberu nevie rozoznať, akú farbu vytiahol?
Poznámka: Ponožka nemôže byť započítaná do dvoch rôznych párov.
21
7 J
Štvorec a pravidelný päťuholník sú vpísané do tej istej kružnice tak, že majú jeden vrchol spoločný. Aký najväčší vnútorný uhol má mnohouholník, ktorý je prienikom nášho štvorca a päťuholníka?
153^\circ
8 J
Koliesko označené číslom 1 má tvar kružnice s priemerom 48\ \text{mm}. Aký priemer musí mať koliesko označené číslom 2, aby mohol celý mechanizmus fungovať?
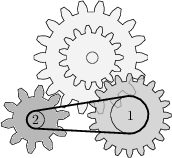
20\ \text{mm}
9 J
Robko si pripravil presný plán, v ktoré dni zo svojich 62-dňových letných prázdnin bude klamať a v ktoré hovoriť pravdu. V k-tý deň jeho prázdnin (pre každé k od 1 do 62) oznámil, že mal v pláne klamať aspoň k dní. Koľko z jeho tvrdení boli klamstvá?
31
10 J
Hráme loďky na štvorčekovom papieri rozmerov 9 \times 9. Náš súper niekde umiestnil svoj Titanic tvaru 5 \times 1 alebo 1 \times 5 štvorčekov. Najmenej koľko krát musíme vystreliť, kým si budeme istí, že sme zasiahli súperov Titanic aspoň raz (vystreliť znamená označiť niektoré políčko z mriežky)?
16
11 J / 1 S
Aký je najväčší možný spoločný deliteľ navzájom rôznych prirodzených čísel a, b, c spĺňajúcich a+b+c=2015?
155
12 J / 2 S
Vlak zásobujúci železiarne pozostáva z lokomotívy (je vždy vpredu) a šiestich vagónov. V každom vagóne je buď uhlie alebo železná ruda. Adam si vlak odfotil, ale nepodarilo sa mu zachytiť ho celý. Na fotke vidno iba vagón so železnou rudou, po ktorom nasledujú dva vagóny s uhlím. Vagóny nie sú úplne symetrické, takže vidíme, že vagón zo železnou rudou je z týchto troch zaradený ako prvý. Koľko rôznych vlakov mohlo byť odfotených tak, že fotografia vyzerá ako Adamova?
31
13 J / 3 S
Objekt postavený z niekoľkých rovnakých kociek vyzerá zozadu ako ’1’ a zhora ako ’3’ (pozri obrázok). Koľko kociek vidíme, keď sa pozeráme sprava, ak vieme, že objekt pozostáva z najväčšieho možného počtu kociek?
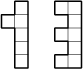
Poznámka: Na obrázku dole je postupne kocka, pohľad na kocku zozadu a zhora.

17
14 J / 4 S
Hovoríme, že prirodzené číslo n je vynikajúce, ak súčet cifier takéhoto čísla je deliteľný 17 a to isté platí pre n+10. Aké je najmenšie vynikajúce číslo?
7999
15 J / 5 S
Autobusová spoločnosť premáva linkou medzi mestami A a D so zastávkami v mestách B a C (v tomto poradí). Cena lístku je priamo úmerná vzdialenosti prejdenej autobusom. Napríklad cestovný lístok z A do C stojí rovnako ako lístky z A do B a z B do C dohromady. Okrem toho spoločnosť neponúka spiatočné lístky, len jednosmerné. Líza, ktorú baví zbieranie autobusových lístkov, chce získať lístky so všetkými možnými cenami bez ohľadu na smer cesty. Zatiaľ má lístky, čo stoja 10, 40, 50, 60 a 70. Aké sú možné ceny chýbajúcich lístkov?
20, 110
16 J / 6 S
Katka obdivuje v hodinárstve hodinky, ktoré sú zabalené v priehľadnej obdĺžnikovej krabici tak, že stred krabice a stred hodiniek (v mieste, kde sa ručičky pretínajú) sa prekrýva. Kratšia strana krabica je 3\text{ cm} dlhá. Všimla si, že na poludnie hodinová ručička ukazuje na stred kratšej strany škatule a o jednej poobede ukazuje na roh krabice. Ako ďaleko od seba sú dva body na okraji krabice, na ktoré ukazuje hodinová ručička o jednej a o druhej hodine poobede?
\sqrt 3\ \text{cm}
17 J / 7 S
Zoraďte cifry 1,2,\ldots,9 do 9-ciferného čísla tak, aby sa každé číslo tvorené dvojicou po sebe idúcich cifier dalo napísať ako súčin k\cdot l nejakých cifier k, l\in\{1,2,\ldots,9\}.
728163549
18 J / 8 S
Nájdi najväčšie prvočíslo p menšie než 210, pričom platí, že 210-p je zložené číslo.
Poznámka: Nezabudni, že číslo 1 nie je prvočíslo ani zložené číslo.
89
19 J / 9 S
V jednej nemenovanej základnej škole sa rozhodli kúpiť určitý počet ceruziek a rozdať ich žiakom prvého ročníka. Žiaci sú rozdelení do tried 1.A, 1.B a 1.C. Ak by ich rozdali všetkým prvákom, každý by dostal 9 ceruziek. Ak by ich rozdali iba v 1.A, každý žiak z 1.A by dostal 30 ceruziek. Nakoniec ak by ich rozdali iba v 1.B, každý žiak z 1.B by dostal 36 ceruziek. Koľko ceruziek by rozdali každému žiakovi 1.C, ak by sa rozdávalo iba v tejto triede?
20
20 J / 10 S
Nájdite všetky 4-ciferné čísla, ktorých prvé dve cifry, posledné dve cifry a samotné číslo sú nenulové štvorce. Na mieste desiatok môže byť aj nula.
1681
21 J / 11 S
Vodič jazdí po diaľnici medzi dvoma mestami konštantnou rýchlosťou. Bohužiaľ, niektoré časti diaľnice opravovali, takže v týchto miestach musel rýchlosť znížiť o štvrtinu. Preto mal za čas, za ktorý bežne dôjde do cieľa prejdených len 6/7 vzdialenosti medzi mestami. Akú časť z cesty, ktorú doteraz prešiel, jazdil po opravovaných častiach diaľnice?
4/7
22 J / 12 S
Obdĺžnik s celočíselnými dĺžkami je rozdelený do 12 štvorcov s dĺžkami: 2, 2, 3, 3, 5, 5, 7, 7, 8, 8, 9, 9. Aký je obvod tohto obdĺžnika?
90
23 J / 13 S
Štvorcový list papiera je zložený tak, že jeden z jeho vrcholov leží na protiľahlej strane. Ako vidno na obrázku, malý trojuholník presahuje. Dĺžka jeho strany, ktorá susedí so stranou listu papiera je 8\ \text{cm} a dĺžka druhej takto susediacej strany je 6\ \text{cm}.
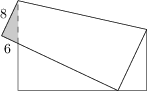
Aká je dĺžka strany štvorcového papiera?
36\ \text{cm}
24 J / 14 S
Starý parník sa pohybuje pozdĺž kanála konštantnou rýchlosťou. Šimon chce zistiť jeho dĺžku. Kým parník pomaly postupuje, Šimon kráča popri vode konštantnou rýchlosťou od zadnej časti parníka k jeho čelu a napočíta 240 krokov. Potom sa okamžite otočí a ide späť až k zadnej časti parníka a napočíta 60 krokov. Aká je dĺžka parníka v krokoch?
96
25 J / 15 S
Číslo 137641=371^2 je najmenšie šesťciferné číslo také, že z neho je možné vyškrtnúť tri navzájom rôzne číslice tak, aby sme dostali jeho druhú odmocninu: \cancel137\cancel6\cancel41. Nájdite najväčšie šesťciferné číslo s touto vlastnosťou.
992016 = 996^2
26 J / 16 S
Linda napísala niečo na kalkulačke a na displeji sa objavilo trojmiestne číslo. Patrik, ktorý sedel oproti nej, si všimol, že z jeho pohľadu (teda dole hlavou) to vyzeralo presne tak, ako trojmiestne číslo, ktoré je o 369 väčšie ako to zadané. Aké bolo číslo, ktoré Linda napísala?
Poznámka: Kalkulačka má sedemsegmentový displej, teda číslice vyzerajú takto:

596
27 J / 17 S
Na ostrove Na-Boi žijú tri rodiny, z ktorých každá ma dvoch synov a dve dcéry. Koľkými spôsobmi môže týchto 12 ľudí vytvoriť 6 manželských párov, ak sú zakázané sobáše súrodencov?
80
28 J / 18 S
Janko a Marienka si upiekli veľmi veľkú pizzu, ktorú rozkrájali na 50 rovnako veľkých kúskov trojuholníkového tvaru. Na kúsky pizze poukladali 1, 2, 3,\ldots, 50 olív postupne v smere hodinových ručičiek. Teraz chcú rozdeliť pizzu na dve rovnaké polovice rovným rezom tak, aby Janko dostal dvakrát toľko olív ako Marienka. Určte celkový počet olív na štyroch plátkoch priliehajúcich k rezu.
68, 136
29 J / 19 S
Nájdi všetky prvočísla p s takou vlastnosťou, že 19p+1 je tretia mocnina celého čísla.
421
30 J / 20 S
V rovnobežníku ABCD leží bod E na strane AD tak, že 2\cdot |AE| = |ED| a bod F leží na strane AB tak, že 2\cdot |AF| = |FB|. Úsečky CF a CE pretínajú uhlopriečku BD v bodoch G a H. Akú časť obsahu rovnobežníka ABCD tvorí päťuholník AFGHE?
\frac{7}{30}
31 J / 21 S
Nájdi najväčšie päťciferné číslo bez nulových číslic, ktoré spĺňa nasledujúce vlastnosti:
- Prvé tri cifry tvoria číslo, ktoré je 9-násobkom čísla tvoreného poslednými dvoma ciframi.
- Posledné tri cifry tvoria číslo, ktoré je 7-násobkom čísla tvoreného prvými dvoma ciframi.
85595
32 J / 22 S
Za kruhovým stolom sedí dvanásť bystrých mužov, ktorí so sebou majú deväť prázdnych kariet a tri špeciálne – označené J, Q a K. Každý z nich náhodne dostal jednu z týchto dvanástich kariet. Každý sa pozrel na svoju kartu a potom ju odovzdal susedovi sediacemu po jeho pravej ruke a takto pokračovali ďalej. Po každom pozretí sa na kartu boli požiadaní, aby zdvihli ruku ak vedia, kto v danej chvíli drží ktorú špeciálnu kartu (ruky dvíhajú naraz). Ani jeden z nich nezdvihol ruku po tom, čo videl štyri karty. Presne jeden muž zdvihol ruku po tom, čo uvidel svoju piatu kartu. Následne x mužov zdvihlo ruku po tom, čo uvideli šesť kariet a y mužov po siedmich kartách. Určte xy.
42
33 J / 23 S
Do rovnoramenného pravouhlého trojuholníka s dĺžkou základne 1 je umiestnených sedem kruhov ako na obrázku:
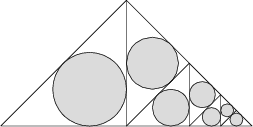
Aký je celkový obsah kruhov?
\pi \frac{3 - 2\sqrt 2}{4} = \pi\frac{(1-\sqrt2)^2}4 = \pi\frac1{4(1+\sqrt2)^2} = \pi\frac1{4(3+2\sqrt2)}
34 J / 24 S
Nájdite všetky prvočísla p také, že p+11 delí p(p+1)(p+2).
7, 11, 19, 79
35 J / 25 S
Žižiavky obyčajné (Porcellio scaber) majú štrnásť nôh. Matka žižiavka má veľké zásoby rovnakých ponožiek a topánok a pripravuje svoje deti na nastávajúce chladné obdobie. Vysvetľuje malej žižiavke Kubovi, že si môže dať ponožky a topánky na nohy v ľubovoľnom poradí, ale je treba mať na pamäti, že na každú jednu nohu je treba navliecť ponožku pred topánkou. Koľkými rôznymi postupmi sa môže malý Kubo obuť?
\frac{28!}{2^{14}}
36 J / 26 S
Nech x je reálne číslo také, že x^3 + 4x = 8. Zistite hodnotu výrazu x^7 + 64x^2.
128
37 J / 27 S
Majme rovnoramenný trojuholník ABC so základňou AB. Priesečník osi uhla ACB so stranou AB označme D a priesečník osi uhla BAC s BC označme E. Nájdite veľkosť uhla BAC, ak |AE| = 2\cdot |CD|.
36^\circ
38 J / 28 S
Majme postupnosť reálnych čísel (a_n) takú, že a_1=2015 a a_1+a_2+\dots+a_n=n^2\cdot a_n pre každé n \geq 1. Nájdite a_{2015}.
\frac1{1008}
39 J / 29 S
Ivka a Janka si vymysleli hru: Ofarbia steny dvoch 12-stenných kociek azúrovou, purpurovou a žltou farbou tak, že každá farba je aspoň na jednej stene každej z kociek. Navyše sú na prvej kocke práve štyri žlté steny. Ak hodia kockami a obe kocky ukazujú rovnakú farbu, Ivka vyhrá, inak vyhrá Janka. Predpokladajme, že farby sú rozdelené tak, že dievčatá majú rovnaké šance na výhru. Koľko stien purpurovej farby musí byť na druhej kocke?
1, 9
40 J / 30 S
Okolo veľkého okrúhleho stola sedí n > 24 žien, pričom každá hovorí iba pravdu alebo iba klame. Každá zo žien tvrdí nasledovné:
- Som pravdovravná.
- Tá, čo sedí o 24 miest ďalej po mojej pravici, je klamárka.
Nájdite najmenšie možné n, pre ktoré toto mohlo nastať.
32
41 J / 31 S
Dva štvorce majú spoločný stred a vrcholy menšieho štvorca ležia na stranách väčšieho štvorca. Ak odstránime menší zo štvorcov, ostanú nám štyri zhodné trojuholníky, každý z nich s obsahom 1/12 väčšieho štvorca. Aká je veľkosť (v stupňoch) najmenšieho z vnútorných uhlov trojuholníka?
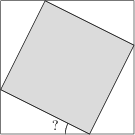
15^\circ
42 J / 32 S
Kružnice \omega_1, \omega_2 s polomermi 1 a 2 sa vnútorne dotýkajú kružnice \omega_3 s polomerom 3. Kružnice \omega_1 a \omega_2 sa navyše dotýkajú zvonku. Body A, B sú na kružnici \omega_3 umiestnené tak, že úsečka AB je spoločnou dotyčnicou \omega_1 a \omega_2. Určte dĺžku úsečky AB.
\frac43 \sqrt{14}
43 J / 33 S
Jedného dňa, Oidipus, neohrozený hrdina stretol sfingu, ktorá mu položila nasledujúci rébus: hľadá prirodzené dvojciferné číslo S. Oidipus mohol vybrať tri jednociferné čísla a < b < c a opýtať sa, či je S nimi deliteľné. Pre každé z týchto čísel dostal odpoveď (buď áno alebo nie). Oidipus začínal byť zúfalý, pretože existovali presne dve čísla spĺňajúce podmienky deliteľnosti. Potom mu sfinga povedala, že sa pomýlila pri deliteľnosti b. To priviedlo Oidipa k nájdeniu čísla S. Aká bola hodnota S?
84
44 J / 34 S
Štyria ľudia jazdia po ceste tým istým smerom, každý nejakou konštantnou rýchlosťou. Prvý šoféruje auto, druhý motorku, tretí skúter a štvrtý ide na bicykli. Šofér auta stretol človeka na skútri o 12.00, cyklistu o 14.00 a motorkára o 16.00. Motorkár stretol človeka na skútri o 17.00 a cyklistu o 18.00. Kedy stretol cyklista človeka na skútri?
15.20
45 J / 35 S
Podlaha miestnosti je pokrytá štvorcovým kobercom so stranou dĺžky 22 metrov. Robotický vysávač (robovač) má za úlohu tento koberec povysávať. Pre jeho pohodlie je koberec rozdelený na 484 rovnakých štvorcových políčok. Robovač, ktorý je rovnako široký ako políčko, sa pohybuje podľa nasledujúcich pravidiel:
- Ak raz povysával políčko, už po ňom nemôže prejsť znovu.
- Robovač sa pohybuje jedným smerom až kým nie je nútený zmeniť ho kvôli kraju koberca alebo už povysávanému políčku.
- Ak robovač musí zmeniť smer a má viacero možností, môže si vybrať, ktorú chce.
Na začiatku je robovač umiestnený na jednom políčku a môže si vybrať ľubovoľný povolený smer. Z koľkých štartovacích políčok vie robovač vyčistiť celý koberec, ak nemusí skončiť pri kraji?
20
46 J / 36 S
Nech body A, B, C, D, E, F ležia v smere hodinových ručičiek na kružnici \omega. Predpokladajme ďalej, že AD je priemer kružnice \omega, BF pretína AD a CE v bodoch G a H, |\sphericalangle FEH| = 56^\circ, |\sphericalangle DGB| = 124^\circ a |\sphericalangle DEC| = 34^\circ. Určte veľkosť \sphericalangle CEB.
22^\circ
47 J / 37 S
Desať ľudí, päť žien a ich manželia, sa zúčastnilo na E párty večierkoch. Vieme, že ani jeden manželský pár sa nezúčastnil na rovnakej párty. Ďalej vieme, že každý pár, ktorý nepozostáva z manželov (vrátane párov rovnakého pohlavia) sa zúčastnil na presne jednej párty a práve jedna osoba sa zúčastnila len na dvoch párty. Pre ktoré najmenšie E to je možné?
14
48 J / 38 S
Študenti dostali ako darček trojciferné číslo \overline{abc}, kde 0 < a < b < c. Ich úlohou bolo vynásobiť ho číslom 6 a potom, aby to bolo zábavné, vymeniť cifry na mieste desiatok a stoviek. Alex to ale nezvládol a vymenil ich pred násobením. Výsledok ale ostal rovnaký! Nájdite \overline{abc}.
678
49 J / 39 S
Máme mriežku 5 \times 3. Myš sediaca v ľavom hornom rohu sa chce dostať ku kúsku syra v pravom dolnom rohu zatiaľ, čo krab sediaci v ľavom dolnom rohu sa chce dostať k riasam v pravom hornom rohu. Presúvajú sa súčasne. Každú sekundu sa myš posunie o štvorec doprava alebo dolu a krab sa presunie o štvorec doprava alebo hore. Koľkými spôsobmi môžu zvieratá dosiahnuť svoj cieľ za predpokladu, že sa ani raz nestretnú?
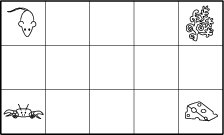
70
50 J / 40 S
Určte počet kladných celých čísel n\le1000 takých, že číslo \lfloor\sqrt[3]{n}\rfloor je deliteľom n.
Poznámka: Symbol \lfloor x\rfloor označuje celú časť čísla x, t. j. najväčšie celé číslo neprevyšujúce x.
172
51 J / 41 S
Nájdi všetky prirodzené čísla m také, že korene rovnice sú strany pravouhlého trojuholníka.
281/2
52 J / 42 S
V košíku máme zelené a červené jablká, aspoň jedno červené a aspoň dve zelené. Pravdepodobnosť, že náhodne vybrané jablko je červené je 42-krát väčšia ako pravdepodobnosť, že dve náhodne vybrané jablká (bez toho, aby sme ich zamieňali) sú obe zelené. Koľko zelených a koľko červených jabĺk je v košíku?
4 zelené a 21 červených
53 J / 43 S
Gilbert Bates, veľmi bohatý muž, si chce dať postaviť nový bazén vo svojej záhrade. Keďže má rád symetriu, záhradníkovi prikázal postaviť bazén v tvare elipsy, ktorý je umiestnený vo štvorci 10\ \text{m}\times 10\ \text{m} ABCD. Tento bazén sa má dotýkať všetkých štyroch strán štvorca, konkrétne na strane AB v bode P, ktorý je vzdialený 2.5\ \text{m} od bodu A. Záhradník, ktorý veľmi dobre vie ako vytvoriť elipsu ak má uvedené ohniská a bod ležiaci na elipse, potrebuje už len vedieť vzdialenosť ohnísk tejto elipsy. Môžete mu pomôcť vypočítať vzdialenosť ohnísk v metroch?
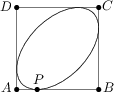
10
54 J / 44 S
Pre postupnosť (a_n) platí, že a_1=1 a a_n=\lfloor\sqrt{a_1+a_2+\dots+a_{n-1}}\rfloor pre n > 1. Určte a_{1000}.
Poznámka: Symbol \lfloor x\rfloor označuje celú časť čísla x, t. j. najväčšie celé číslo neprevyšujúce x.
495
55 J / 45 S
Určte počet všetkých takých tabuliek 4 \times 4 vyplnených nezápornými celými číslami, že platí
- každý riadok a každý stĺpec obsahuje najviac dve nenulové čísla,
- súčet čísel v každom riadku a v každom stĺpci je 3.
576






















