1 J
E.T. měl balvan ve tvaru krychle, jehož objem byl 216\,\text{m}^3, a vysekl z něj kvádr o rozměrech 1\,\text{m}\times 1\,\text{m}\times 2\,\text{m} způsobem ukázaným na obrázku. Jaký má nyní balvan povrch (v \text{m}^2)?

216
2 J
Dva přátelé, David a Štěpán, vyhráli jackpot a koupili si krásnou obdélníkovou parcelu o rozměrech 35\,\text{m} \times 25\,\text{m}. Chtějí si na ní postavit dvojdomek se společnou zahradou G o ploše 300\, \text{m}^2. Půdorys parcely je znázorněn na obrázku:
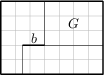
(Vzdálenost sousedních čar čtvercové sítě je 5\,\text m.) Jak daleko musí zeď b zasahovat z jedné poloviny dvojdomku do druhé, aby měly obě části stejnou plochu?
8{,}75\, \text{m}
3 J
Malý Rado se chce vypravit na pláž. Doma vyhrabal patery různé plavky, tři slamáky, čtvero slunečních brýlí a pět triček. Aby na pláži nevzbudil pohoršení, musí si obléct plavky (právě jedny). Brýle, slamák ani tričko nikterak povinné nejsou, od každého z těchto doplňků si může vzít nanejvýš jeden kus. Kolika různými způsoby se Rado může obléci, aniž by vzbudil pohoršení?
600
4 J
Martina strávila prázdniny v deštném pralese. Každý den pršelo – buď ráno, nebo odpoledne, nebo celý den. Dohromady prožila 13 dní, kdy nepršelo celou dobu. Ranní déšť ji zastihl jedenáctkrát a odpolední dvanáctkrát. Jak dlouhé byly Martininy prázdniny?
18 dní
5 J
Najděte nejmenší nezáporné celočíselné řešení rovnice n-2\cdot \operatorname{Q}(n)=2016, kde \operatorname{Q}(n) označuje ciferný součet čísla n.
2034
6 J
Kolik existuje kladných celých čísel, jejichž první číslice (tj. ta nejvíce vlevo) se rovná počtu jejich cifer?
111\,111\,111
7 J
Chodník se skládá z mnoha dlaždic. Jedna z nich má tvar pravidelného n-úhelníka a je ze všech stran obklopena ostatními dlaždicemi. Když dlaždici otočíme o 48^\circ kolem jejího středu, přesně zapadne do své původní polohy. Jaká je nejmenší možná hodnota n?
15
8 J
O dnu budeme říkat, že je šťastný, jestliže se jeho datum zapsané v podobě DD.MM.RRRR skládá z osmi různých cifer – zde DD určuje den, MM měsíc a RRRR rok, přičemž pokud je číslo udávající den nebo měsíc menší než deset, přidáváme před něj nulu. Například 26.04.1785 byl šťastný den. Jaký je nejbližší šťastný den (ode dneška)?
17. června 2345
9 J
Kuba má kvádr. Zajímalo by ho, kolik rovin obsahuje právě čtyři jeho vrcholy. Poraďte mu.
12
10 J
Míša se rozhodla nakreslit pomocí pravítka a kružítka dobře vypadající půlměsíc. Začala nakreslením kružnice se středem M_1 a poloměrem r_1=3\ \text{cm}. Potom zabodla kružítko do bodu M_2 ležícího na kružnici a nakreslila druhou kružnici o poloměru r_2, která protla původní kružnici v protilehlých bodech ležících na průměru procházejícím M_1, jak ukazuje obrázek.
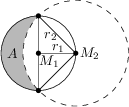
Jakou plochu má půlměsíc A v \text{cm}^2?
9
11 J / 11 S
Královna chobotnic má čtyři služebnice, z nichž každá má šest, sedm, nebo osm chapadel. Ty, které mají sedm chapadel, stále lžou, zatímco ty se šesti nebo osmi chapadly mluví vždy pravdu. Jednoho dne královna chobotnic svolala všechny své služebnice a zeptala se jich, kolik mají dohromady chapadel. První odpověděla, že 25, druhá tvrdila, že 26, třetí řekla 27 a poslední 28. Kolik chapadel mají dohromady pravdomluvné služebnice?
6
12 J / 12 S
V supermarketu prodávají mléčnou, bílou a hořkou čokoládu, všechny za stejnou cenu. Jednoho krásného dne činila tržba za prodanou mléčnou čokoládu 270,–, za bílou čokoládu 189,– a za hořkou 216,–. Kolik nejméně tabulek čokolády se ten den mohlo prodat?
25
13 J / 13 S
Otec pěti dětí chce svojí rodině nakoupit zákusky ke svačině. Léta bolestných zkušeností ho naučila, že musí dětem sehnat buď pět stejných, nebo pět vzájemně různých zákusků, jinak se jeho ratolesti do krve pohádají.Po dlouhé diskuzi, během níž se ani trochu nepodařilo domluvit, jaké zákusky by se měly nakoupit, naštvaně poručil svojí nejmladší dceři Aničce: „Půjdeš do cukrárny a řekneš prodavačce, ať ti dá x kousků náhodně! Až se vrátíš, každé z vás dětí dostane jeden zákusek a všechny ostatní budou pro mě a pro maminku!“ Víme, že v cukrárně vedou alespoň pět druhů zákusků a vždycky mají ode všech dostatečné množství. Jaké číslo x otec vybral, aby vynaložil co nejméně peněz a zároveň se jeho děti v žádném případě nepohádaly?
17
14 J / 14 S
Jaký je poměr obsahu kruhu ku obsahu čtverce, mají-li stejný obvod?
4 : \pi
15 J / 15 S
V únoru se Olin rozhodl provětrat svůj soukromý tryskáč a navštívit Kokosové ostrovy. Ze svého evropského sídla odletěl v 10:00 středoevropského času (SEČ) a přistál na ostrovech následující den v 5:30 tamního času (KČ). Domů odlétal v 8:30 KČ a přistál stejného dne v 17:00 SEČ. Předpokládejme, že oba lety trvaly stejně dlouho. Kolik bylo hodin na Kokosových ostrovech, když se Olin vrátil domů?
22:30
16 J / 16 S
Trojice čísel 14, 20, n má následující vlastnost: Součin každých dvou z nich je dělitelný tím třetím. Najděte všechna kladná celá čísla n, pro něž je tato podmínka splněna.
70, 140, 280
17 J / 17 S
Úsečka x dělí obdélník na dva lichoběžníky způsobem ukázaným na obrázku. Vzdálenost |PA| je rovna 10\,\text{cm} a |AQ| je 8\,\text{cm}. Lichoběžník T_1 má plochu 90\,\text{cm}^2, lichoběžník T_2 plochu 180\,\text{cm}^2.
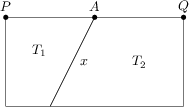
Jaká je délka úsečky x v \text{cm}?
17
18 J / 18 S
Paní Leontýna natrhala na zahradě jahody. Chce je rozdat svým čtyřem synům tak, aby každý z nich dostal alespoň tři, přičemž Vilibald jich dostane více než Bonifác, Bonifác více než Ferdinand a Ferdinand více než Mikuláš. Každý ze synů bude znát počet svých jahod, celkové množství rozdělených jahod i podmínky, které si jejich mamá vymyslela. Jak má Leontýna rozdělit jahody, aby jich využila co nejméně a zároveň aby žádný z chlapců neznal celé rozdělení?
(M,\, F,\, B,\, V) = (3,\, 5,\, 6,\, 8)
19 J / 19 S
Na obvod kruhu napíšeme po směru hodinových ručiček všechna přirozená čísla od 1 do 1000 ve vzestupném pořadí. Následně budeme některá z čísel označovat: Začneme jedničkou a pak označíme každé patnácté číslo (tj. 16, 31 atd.). Pokračujeme tak dlouho, dokud neoznačíme některé číslo podruhé. Kolik čísel zůstane neoznačených, když skončíme?
800
20 J / 20 S
Zjistěte součet velikostí sedmi označených vnitřních úhlů této sedmicípé hvězdy (ve stupních).
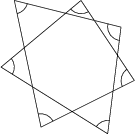
540^\circ
21 J / 21 S
Žáci dostali za úkol spočítat aritmetický průměr čísel 1, 3, 6, 7, 8 a 10. Pepíček ale zvolil špatný přístup: Nejdřív si vybral některá dvě čísla a spočítal jejich průměr. Potom vzal výsledek a některé další číslo a zase vypočítal aritmetický průměr. Tak pokračoval, dokud nevyužil všechna čísla. Jaké největší absolutní hodnoty chyby (tj. absolutní hodnoty rozdílu svého a správného výsledku) tak mohl dosáhnout?
17/6
22 J / 22 S
Na jedné straně rovné silnice je pět pouličních lamp L_1, L_2, L_3, L_4 a L_5 uspořádaných s jednotným rozestupem 12\, \text{m} v jedné přímce. Na druhé straně silnice stojí stánek se zmrzlinou. Když Honza postává u vchodu do obchodu v bodě E, vidí úsek mezi lampami L_1 a L_2 pod úhlem \alpha = 27^\circ. Pokud si stoupne k lampě L_5, vidí úsek mezi body L_1 a E rovněž pod úhlem 27^\circ.
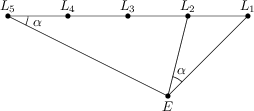
Jak daleko jsou od sebe L_1 a E?
24\, \text{m}
23 J / 23 S
Šavlík si vybral dvě různá celá čísla od 1 do 17 (včetně) a vynásobil je. Kupodivu se ukázalo, že výsledný součin je rovný součtu zbylých patnácti čísel. Nalezněte Šavlíkovu dvojici čísel.
10 a 13
24 J / 24 S
Kolik šestic kladných celých čísel (a, b, c, d, e, f) splňuje a > b > c > d > e > f a zároveň a+f = b+e = c+d = 30?
\binom{14}{3}=364
25 J / 25 S
K časované bombě je připojený displej ukazující čas zbývající do výbuchu (v minutách a vteřinách). Na začátku odpočtu je na displeji 50:00. Žárovka blikne, kdykoliv je zobrazovaný počet minut rovný počtu vteřin (např. 15:15) nebo když je číslo na displeji stejné při čtení zleva i zprava (např. 15:51). V okamžiku, kdy žárovka blikne posedmdesáté, můžeme bombu zneškodnit. Jaký čas bude v tu chvíli na displeji?
03:03
26 J / 26 S
Pět kruhů se vzájemně dotýká způsobem znázorněným na obrázku. Určete poloměr nejmenšího kruhu, jestliže velký kruh má poloměr 2 a zbylé dva kruhy s vyznačenými středy mají poloměr 1.
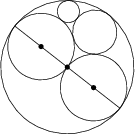
\frac 13
27 J / 27 S
V kasinu sedělo kolem velkého stolu několik hráčů rulety. Když se zvedl Vejtek a s ním i jeho 16\,000 euro, průměrná hotovost připadající na jednoho hráče poklesla o 1\,000 euro. O dalších 1\,000 pak klesla, když si přisedli gambleři Marta a Tonda, každý vybavený pouhými 2\,000 euro. Kolik hráčů sedělo u stolu, když ještě Vejtek hrál?
9
28 J / 28 S
V krychli 7\times7\times7 je každá dvojice sousedících krychliček jednotkového objemu oddělená přepážkou. Odebráním několika přepážek chceme dosáhnout toho, že bude každá krychlička spojená s alespoň jednou z krychliček na povrchu. Jaké nejmenší množství přepážek je třeba odebrat?
125
29 J / 29 S
Víme, že 20{\ast}{\ast}{\ast} 16 je sedmiciferné číslo, které je druhou mocninou nějakého celého čísla. Které tři cifry chybějí?
909
30 J / 30 S
Trojúhelník ABC s délkami stran |AB| = |AC| = 5\,\text{m} a |BC| = 6\,\text{m} je částečně napuštěný vodou. Když trojúhelník leží na straně BC, je hladina ve výšce 3\,\text{m} nad touto stranou. Pokud bude trojúhelník spočívat na straně AB, jaká bude výška vodou naplněné části? Uvádějte v metrech.
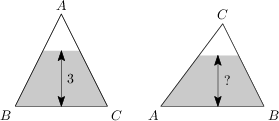
18/5
31 J / 31 S
Máme šest beden označených 1 až 6 a v nich nějak rozdělených 17 broskví. Jediný krok, který smíme udělat, je následující: Jestliže je v n-té bedně právě n broskví, jednu sníme a zbylých n-1 rozdělíme po jedné do beden 1 až n-1. Jak jsou broskve rozdělené, jestliže víme, že nám jejich rozložení umožňuje postupně sníst všechny?
1,1,3,2,4,6
32 J / 32 S
Na vrchol hory vede jednoduchá lanovka s pevně připojenými dvojicemi sedadel. Celkem 74 lidí chce vyjet nahoru, zatímco 26 pasažérů čeká u horní stanice na cestu zpět. Přesně v poledne se mechanismus spustí a na obou stanicích nasedne do lanovky první dvojice; ostatní cestující pak plynule nastupují, kdykoli přijede další sedačka. Ve 12:16 se dvojsedačka vezoucí první dva cestující vzhůru setká s poslední obsazenou dvojsedačkou směřující dolů. Ve 12:22 naopak sedačka vezoucí první dvojici směrem dolů mine poslední obsazenou sedačku směřující na vrchol. Sedačky jsou podél lana rozmístěny rovnoměrně (tj. ve stejných vzájemných vzdálenostech), lanovka se pohybuje stálou rychlostí a všichni cestující jezdí ve dvojicích. Kolik minut trvá jízda ze spodní stanice do horní?
26
33 J / 33 S
Mějme kosočtverec ABCD a body M, N ležící na úsečkách AB, BC různé od A, B, C takové, že DMN je rovnostranný trojúhelník a |AD| = |MD|. Určete velikost úhlu ABC (ve stupních).
100^\circ
34 J / 34 S
Kolika způsoby je možné obarvit políčka tabulky 2 \times 7 žlutě a zeleně tak, aby v žádném místě nevzniklo ani zelené, ani žluté L-trimino?
Poznámka: L-trimino je následující tvar (případně otočený o nějaký násobek pravého úhlu):

130
35 J / 35 S
Filip je nadšeným sběratelem diamantů, ale zatím jich vlastní méně než 200. Aby se jimi mohl lépe kochat, rozdělil všechny své diamanty do několika (nejméně dvou) hromádek tak, že
- každá hromádka se skládá z jiného počtu diamantů,
- na žádné hromádce nejsou právě dva diamanty,
- pro každou hromádku platí, že kdykoli by byla rozdělena na dvě menší části, skládala by se alespoň jedna z nich ze stejného počtu diamantů jako některá z nerozdělených hromádek.
Jaké největší množství diamantů může Filip vlastnit?
Poznámka: Hromádka musí vždy obsahovat alespoň jeden diamant.
196
36 J / 36 S
Ve hře kámen, nůžky, papír máme tři možné symboly: kámen K, nůžky N a papír P. Přitom K>N, N>P, P>K a K=K, N=N, P=P, kde A>B značí, že A vítězí nad B, a A=B znamená remízu. Turnaj v obouruční hře kámen, nůžky, papír bez opakování sestává z devíti her, které proti sobě hrají dva hráči oběma rukama současně, a to levou proti levé a pravou proti pravé. Za vítězství získává hráč 2 body, za remízu 1 a za prohru 0 bodů. V jedné hře se tedy mezi hráče rozdělí celkem čtyři body. Během turnaje musí každý hráč zahrát každou možnou (uspořádanou) dvojici symbolů právě jednou. Jaká je pravděpodobnost, že všech devět her turnaje skončí skórem 2:2, volí-li oba hráči dvojice symbolů náhodně?
3!^3/9!=1/1680
37 J / 37 S
Síť tělesa sestává z osmi rovnostranných trojúhelníků a šesti čtverců jako na obrázku.
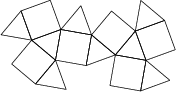
Je-li délka každé hrany 1\,\text{km}, jaký je objem tělesa (v \text{km}^3)?
\frac 53 \sqrt 2
38 J / 38 S
Najděte jediného trojciferného prvočíselného dělitele čísla
601
39 J / 39 S
Třináct včel – jedna malá a dvanáct velkých – žije v plástvi o 37 buňkách. Každá velká včela zabere tři po dvou sousední buňky, zatímco malá včela obsadí jen jednu buňku (viz obrázek). Kolika způsoby může být plástev rozdělena na třináct nepřekrývajících se sektorů tak, aby je mohlo všech třináct včel obsadit v souladu s popsanými požadavky?
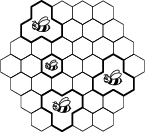
20
40 J / 40 S
Do kružnice \omega je vepsán rovnostranný trojúhelník ABC. Na kratším oblouku BC kružnice \omega zvolme bod X a označme T průsečík AB s CX. Je-li |AX| = 5 a |TX| = 3, určete |BX|.
15/8
41 J / 41 S
Uvažme rovnostranný trojúhelník ABC. Vnitřní bod P trojúhelníka ABC nazveme zářivým, pokud lze najít přesně 27 paprsků vycházejících z P a protínajících strany trojúhelníka ABC takových, že trojúhelník je těmito paprsky rozdělen na 27 menších trojúhelníků stejného obsahu. Určete počet zářivých bodů v trojúhelníku ABC.
\binom{26}{2} = 325
42 J / 42 S
Kolik kladných dělitelů čísla 2016^2 menších než 2016 nedělí číslo 2016?
47
43 J / 43 S
Nechť Spočtěte Z_1 + Z_2 + \dots + Z_{2016}.
\frac12 (4033\sqrt{4033} - 1)
44 J / 44 S
Posloupnost celých čísel a_0, a_1, a_2 \dots je konstruována následujícím způsobem: Je-li a_i dělitelné třemi, položíme a_{i+1}=a_i /3, v opačném případě položíme a_{i+1}=a_i +1. Pro kolik různých nezáporných celých čísel a_0 dosáhne tato posloupnost poprvé hodnoty 1 po přesně jedenácti krocích (tj. a_{11} = 1, ale a_0, a_1, \dots, a_{10} \neq 1)?
423
45 J / 45 S
Nechť ABCD, AEFG a EDHI jsou obdélníky se středy po řadě K, L a J. Předpokládejme dále, že A, D, E jsou po řadě vnitřní body úseček HI, FG, BC a že |\sphericalangle AED| = 53^\circ. Určete velikost \sphericalangle JKL (ve stupních).
74^\circ
46 J / 46 S
Bára si vybrala několik (ne nutně různých) čísel z množiny \{-1, 0, 1, 2\} takovým způsobem, že jejich součet je roven 19 a součet jejich druhých mocnin je 99. Jaké největší hodnoty může nabývat součet třetích mocnin Bářiných čísel?
133
47 J / 47 S
Najděte největší devíticiferné číslo s následujícími vlastnostmi:
- žádná číslice se v něm nevyskytuje více než jednou,
- vyškrtneme-li jeho k-tou cifru (pro k=1,2,\ldots,9), dostaneme osmiciferné číslo dělitelné k.
876\,513\,240
48 J / 48 S
Je dán obdélník ABCD se stranou AB délky 12 a bod P ležící uvnitř tohoto obdélníka. Pro každý z trojúhelníků ABP, BCP a DAP platí, že jeho obvod je roven jeho obsahu. Jaký je obvod trojúhelníka CDP?
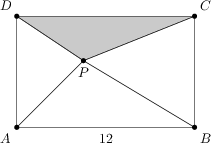
25
49 J / 49 S
Na tabuli je napsaná (uspořádaná) dvojice čísel (0,0). V každém kroku smažeme aktuální dvojici (a,b) a napíšeme místo ní dvojici (a+b+c, b+c), kde c je rovno buď 247, nebo -118 (z těchto dvou hodnot si můžeme v každém kroku vybrat). Najděte nejmenší nenulový počet kroků, po kterém se na tabuli může objevit dvojice (0,b) pro nějaké b.
145
50 J / 50 S
Cikcak je lomená čára, která vznikne ze dvou rovnoběžných polopřímek opačného směru spojením jejich počátečních bodů. Na kolik nejvíce oblastí může deset cikcaků rozdělit rovinu?
416
51 J / 51 S
Mějme čtyřstěn, jehož každá stěna je trojúhelník se stranami délek 1, \sqrt 2 a c. Poloměr sféry opsané tomuto čtyřstěnu je 5/6. Najděte c.
\sqrt{23}/3
52 J / 52 S
Na uvítací přípitek vyrovnal vrchní číšník do řady 2016 sklenek s vynikajícím višňovým koktejlem. Pikolík dostal za úkol jednu z nich překrýt stříbrným táckem, na něj postavit sošku a do ostatních rozmístit lichý počet višní tak, aby v každé sklence byla nejvýše jedna. Navíc mělo napravo od sklenky překryté táckem skončit více višní než nalevo od ní. Kolika způsoby to pikolík může provést?
2016\cdot 2^{2013}
53 J / 53 S
Jirka měl dřevěnou krychli. Protože nebyl spokojen s její barvou, rozhodl se ji natřít nazeleno. Ani to ho ale neuspokojilo, a tak si usmyslel, že ji rozřeže na malé kvádry. Vybral si proto 33 různých rovin, z nichž každá se nacházela mezi některými dvěma protilehlými stěnami krychle a byla s nimi rovnoběžná, a provedl podél nich řezy. Když se krychle rozpadla, spočítal všechny kvádry s alespoň jednou zelenou stěnou a s údivem zjistil, že je jich stejně jako kvádrů, které nemají žádnou zelenou stěnu. Na kolik kvádrů mohl krychli rozřezat?
1260 nebo 1344 (dvě řešení)
54 J / 54 S
Pro přirozené číslo n definujme p(n) jako součin všech nenulových cifer čísla n. Najděte největšího prvočíselného dělitele čísla p(1)+\dots+p(999).
103
55 J / 55 S
Nechť (a_n)_{n=1}^\infty je rostoucí posloupnost kladných celých čísel taková, že 9\mid a_{3k-2}, 14\mid a_{3k-1} a 19\mid a_{3k} pro každé přirozené číslo k. Najděte nejmenší možnou hodnotu a_{2016}.
14478
56 J / 56 S
Uvnitř trojúhelníka ABC se nachází bod P. Průsečíky přímek AP, BP a CP s protilehlými stranami označme postupně D, E a F. Spočtěte obsah trojúhelníka ABC, pokud víte, že | PA |=6, | PB | =9, | PD |=6, | PE | =3 a | CF | =20.
108
57 J / 57 S
Najděte poslední dvojčíslí před desetinnou čárkou čísla (7 + \sqrt{44})^{2016}.
05






















