1 J
Aus einem würfelförmigen Felsblock mit einem ursprünglichen Volumen von 216\,\text{m}^3 wurde ein quaderförmiges Stück der Größe 1\,\text{m}\times 1\,\text{m}\times 2\,\text{m} gehauen, wie in der Abbildung zu sehen ist. Wie groß ist die Oberfläche des neu entstandenen Objekts in \text{m}^2?

216
2 J
Die beiden Freunde Christoph und Jonas haben den Jackpot geknackt und ein rechteckiges Grundstück mit den Seitenlängen 35\,\text{m} und 25\,\text{m} erworben. Sie wollen es mit einem Doppelhaus bebauen und den 300\,\text{m}^2 großen Garten G gemeinsam nutzen. Der Grundriss ist wie folgt:
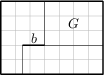
Dabei beträgt der Abstand zweier Gitterlinien 5\,\text m. Wie lang ist die Mauer b, mit der das eine Haus in das andere hineinragt, wenn beide Häuser die gleiche Grundfläche haben sollen?
8.75\, \text{m}
3 J
Klein Markus möchte zum Baden an den Strand gehen. Er besitzt folgende unterscheidbare Badeutensilien: 5 Badehosen, 3 Strohhüte, 4 Sonnenbrillen und 5 T-Shirts. Die Strandbaderegeln schreiben vor, dass Markus eine Badehose tragen muss. Das Tragen von Strohhut, Sonnenbrille und T-Shirt ist nicht verpflichtend. Wenn er sich jedoch noch mit zusätzlichen Utensilien kleidet, benutzt er aus jeder Kategorie höchstens eines. Auf wie viele verschiedene Arten kann Markus korrekt gekleidet am Strand erscheinen?
600
4 J
Laura verbrachte ihren Urlaub im Regenwald. Jeden Tag regnete es entweder am Vormittag oder am Nachmittag oder aber den ganzen Tag lang. Es gab 13 Tage, an denen es zu Lauras Freude nicht den ganzen Tag regnete. Allerdings erlebte sie genau 11 verregnete Vormittage und 12 verregnete Nachmittage. Wie lange war Lauras Urlaub?
18 Tage
5 J
Finde die kleinste nicht-negative ganze Zahl, die Lösung der Gleichung ist!
Hierbei steht \operatorname{Q}(n) für die Quersumme der Zahl n.
2034
6 J
Wie viele positive ganze Zahlen haben die Eigenschaft, dass ihre erste Ziffer (von links gelesen) mit der Anzahl ihrer Ziffern übereinstimmt?
111\,111\,111
7 J
Eine Bodenpflasterung besteht aus vielen verschiedenartigen Fliesen, von denen eine die Form eines regulären n-Ecks hat und rundherum nahtlos von anderen Fliesen umgeben ist. Wenn man diese eine Fliese herausnimmt und sie um 48^\circ um ihren Mittelpunkt dreht, so passt sie wieder an ihren Platz. Wie lautet die kleinste Zahl n, für die das möglich ist?
15
8 J
Ein Tag soll Glückstag heißen, wenn sein im Format TT.MM.JJJJ geschriebenes Datum aus acht verschiedenen Ziffern besteht. Dabei steht TT für den Tag, MM für den Monat und JJJJ für das Jahr, wobei Tage und Monate unter 10 mit führender Null geschrieben werden. Beispielsweise war der 26.04.1785 ein Glückstag. Wann wird vom heutigen Tag aus gesehen der nächste Glückstag sein?
17.06.2345
9 J
Wie viele Ebenen gibt es, die genau vier Ecken eines gegebenen Quaders enthalten?
12
10 J
Klein Sandra möchte mit Zirkel und Lineal eine schöne Mondsichel zeichnen. Zuerst zieht sie einen Kreis um einen Punkt M_1 mit dem Radius r_1=3\,\text{cm}. Anschließend wählt sie einen Punkt M_2 auf der Kreislinie und zeichnet einen zweiten Kreis um M_2 mit einem Radius r_2, so dass die beiden Schnittpunkte mit dem ersten Kreis auf einem Durchmesser durch M_1 liegen, wie in der Skizze zu sehen ist.
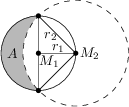
Wie groß ist der Flächeninhalt der Mondsichel A in \text{cm}^2\,?
9
11 J / 11 S
Alle Diener von König Octopus haben sechs, sieben oder acht Beine. Diejenigen mit sieben Beinen lügen immer, die mit sechs oder acht Beinen sagen immer die Wahrheit. Eines Tages versammelte der König vier seiner Diener und fragte sie, wie viele Beine die vier insgesamt hätten. Der erste Diener antwortete, dass die Gesamtzahl an Beinen 25 ist, der nächst behauptete, es seien 26, der dritte sagte 27 und der letzte gab 28 als Antwort. Wie viele Beine hatten die Wahrheit sagenden Diener unter diesen vieren dabei insgesamt?
6
12 J / 12 S
Ein Kiosk bietet Schokoladentafeln der Sorten Milchschokolade, weiße Schokolade und dunkle Schokolade zum gleichen Preis an. Eines Tages wurden Milchschokoladentafeln für 270 Euronen verkauft, weiße Schokoladentafeln für 189 Euronen und dunkle Schokoladentafeln für 216 Euronen. Was ist die kleinste Gesamtanzahl an Schokoladentafeln, die an diesem Tag verkauft worden sein könnten?
25
13 J / 13 S
Ein Vater von fünf Kindern möchte für seine Familie für den Nachmittagstee Gebäckstücke besorgen. Er weiß aus leidvoller Erfahrung, dass er entweder allen Kindern dieselbe Gebäcksorte geben oder lauter verschiedene Gebäckstücke verteilen muss. Andernfalls bricht Streit unter den Kindern aus.
Als eines Tages nach langer Diskussion um die Art der Gebäckstücke keine Einigung erreicht werden konnte, wies der Vater entnervt seine jüngste Tochter Anna an: Du gehst jetzt in die Bäckerei und sagst der Verkäuferin, dass sie dir ganz willkürlich x Gebäckstücke geben soll! Wenn Du damit wieder zurück bist, bekommt jedes Kind genau eines davon, die verbleibenden erhalten Mama und Papa! Er sagte dies im Wissen, dass die Bäckerei mehr als fünf verschiedene Sorten an Gebäck anbietet und dass von jeder Sorte auch reichlich Gebäckstücke vorhanden sind.
Welche Anzahl x an Gebäckstücken wählte der Vater, so dass auf alle Fälle der Familienfriede gewahrt werden konnte und gleichzeitig seine Unkosten möglichst gering gehalten wurden?
17
14 J / 14 S
In welchem Verhältnis stehen die Flächeninhalte eines Kreises und eines Quadrates, wenn beide geometrischen Figuren denselben Umfang besitzen?
Notiere das Verhältnis in der Form Flächeninhalt des Kreises zu Flächeninhalt des Quadrats !
4 : \pi
15 J / 15 S
Im letzten Februar besuchte Steven die Kokos-Inseln mit seinem Privatjet. Er startete von seiner Villa in Europa um 10:00 Uhr Mitteleuropäischer Zeit (MEZ) und landete auf den Kokos-Inseln am darauf folgenden Tag um 5:30 Uhr Ortszeit (Cocos Islands Time, CCT). Als er wieder zurück flog, startete er um 8:30 Uhr CCT und landete um 17:00 Uhr MEZ des selben Tages zu Hause. Sein Hinflug dauerte genau so lange wie sein Rückflug. Wie viel Uhr war es auf den Kokos-Inseln, als Steven in Europa landete?
22:30 Uhr
16 J / 16 S
Bestimme alle positiven ganzen Zahlen n, so dass für die Zahlen 14, 20 und n die folgende Bedingung erfüllt ist:
Wenn man irgendwelche zwei dieser drei Zahlen multipliziert, so ist das Ergebnis stets durch die dritte Zahl teilbar.
70, 140, 280
17 J / 17 S
Ein Rechteck wird durch die Strecke x in zwei Trapeze T_1 und T_2 zerlegt, wie in der Skizze zu sehen ist. Dabei sind die Längen \overline{PA} = 10\,\text{cm} und \overline{AQ}= 8\,\text{cm} sowie die Flächeninhalte \operatorname{F} (T_1) = 90\,\text{cm}^2 und \operatorname{F} (T_2) = 180\,\text{cm}^2 gegeben.
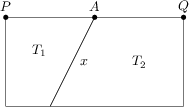
Wie lang ist die Strecke x in \text{cm}?
17
18 J / 18 S
Elisabeth erntet Erdbeeren aus dem eigenen Garten. Sie möchte die Beeren unter ihren vier Söhnen verteilen und zwar so, dass sie jedem von ihnen mindestens drei Erdbeeren gibt und dass Valentin dabei mehr Erdbeeren als Benedikt, Benedikt mehr als Ferdinand und Ferdinand mehr als Michael bekommt. Jeder Junge kennt die Anzahl der Beeren, die er selber erhalten hat, die Anzahl der insgesamt verteilten Erdbeeren sowie die oben beschriebenen Verteilungsregeln. Wie sollte Elisabeth die Erdbeeren verteilen, damit sie möglichst wenige Beeren austeilen muss und keiner ihrer Söhne die komplette Verteilung herausfinden kann?
Notiere eine Verteilung in der Form (M,\, F,\, B,\, V).
(3,\, 5,\, 6,\, 8)
19 J / 19 S
Die natürlichen Zahlen von 1 bis 1000 werden der Reihe nach im Uhrzeigersinn entlang einer Kreislinie aufgeschrieben. Beginnend mit der 1 wird im Uhrzeigersinn jede fünfzehnte Zahl markiert, also 1, 16, 31, usw. Diese Prozedur wird so lange fortgeführt, bis eine Zahl markiert werden muss, die bereits eine Markierung besitzt. Wie viele nicht markierte Zahlen sind am Ende dieses Verfahrens vorhanden?
800
20 J / 20 S
Bestimme die Summe der sieben markierten Innenwinkel dieses 7-zackigen Sterns in Grad!
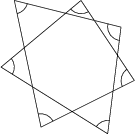
540^\circ
21 J / 21 S
Die Schüler sollten das arithmetische Mittel der Zahlen 1, 3, 6, 7, 8 und 10 ausrechnen. Doch leider hatte Lucy einen falschen Ansatz gemacht: Sie wählte zwei der Zahlen und berechnete deren arithmetisches Mittel. Anschließend bildete sie das arithmetische Mittel aus ihrem Ergebnis und einer weiteren Zahl aus der Liste. Sie fuhr so mit ihrer Berechnung fort, bis sie alle gegebenen Zahlen abgearbeitet hatte. Wie groß ist die größtmögliche Abweichung zum tatsächlichen Ergebnis, die man mit Lucys Art der Berechnung erreichen kann?
\frac{17}{6}
22 J / 22 S
Fünf kleine Straßenlaternen L_1, L_2, L_3, L_4 und L_5 stehen im Abstand von je 12\,\text{m} auf einer Seite einer geraden Straße. Auf der gegenüber liegenden Straßenseite befindet sich eine Eisdiele. Steht Julien vor dem Eingang E der Eisdiele, so sieht er die Laternen L_1 und L_2 unter einem Winkel von \alpha=27^\circ. Steht er an der Laterne L_5, so sieht er L_1 und E auch unter dem Winkel 27^\circ.
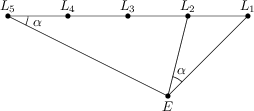
Wie groß ist der Abstand von L_1 nach E?
24\, \text{m}
23 J / 23 S
Nadja wählte aus den Zahlen 1, 2, 3, , 17 zwei verschiedene aus und multiplizierte sie. Zu ihrem Erstaunen war der Wert dieses Produktes gleich der Summe der fünfzehn Zahlen, die sie nicht ausgewählt hatte. Welche Zahlen hatte Nadja sich ausgesucht?
10 und 13
24 J / 24 S
Wie viele 6-Tupel (a, b, c, d, e, f) positiver ganzer Zahlen erfüllen die Bedingungen a > b > c > d > e > f und a+f = b+e = c+d = 30 gleichzeitig?
\binom{14}{3}=364
25 J / 25 S
Eine Zeitbombe ist mit einem Display ausgestattet, das die Zeit bis zur Explosion in Minuten und Sekunden anzeigt. Das Rückwärtszählen beginnt mit der Anzeige 50:00 am Display. Jedesmal wenn die angezeigte Zahl an Minuten gleich der angezeigten Zahl an Sekunden ist (beispielsweise 15:15) oder wenn die Zahl auf dem Display von rechts gelesen die gleiche ist wie die angezeigte Zahl (wie bei 15:51), dann blinkt ein Lämpchen auf. Die Bombe kann deaktiviert werden, wenn das Lämpchen zum 70. Mal aufleuchtet. Welche Zeit wird auf dem Display angezeigt, wenn die Bombe deaktiviert werden kann?
03:03
26 J / 26 S
Fünf Kreise berühren einander, wie in der Abbildung zu sehen ist. Finde den Radius des kleinsten Kreises, wenn der Radius des größten Kreises 2 ist und die beiden anderen Kreise mit den markierten Mittelpunkten jeweils den Radius 1 haben.
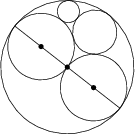
\frac 13
27 J / 27 S
Im Casino sitzen einige Leute beim Roulette an einem großen Tisch. Als Erich mit seinem Guthaben von 16\,000 Euronen den Tisch verlässt, sinkt das durchschnittliche Guthaben aller Spieler um 1\,000 Euronen. Es vermindert sich nochmal um 1\,000 Euronen, als die beiden Zockerinnen Bettina und Elfi an diesem Tisch mit jeweils 2\,000 Euronen einsteigen. Wie viele Spieler saßen am Tisch, als Erich noch mitspielte?
9
28 J / 28 S
In einem 7\times7\times7–Würfel sind je zwei benachbarte Einheitswürfel durch ein Begrenzungsquadrat voneinander getrennt. Es sollen nun Begrenzungsquadrate so entfernt werden, dass jeder Einheitswürfel mit mindestens einem der äußersten Einheitswürfel verbunden ist. Wie groß ist die minimale Anzahl der Begrenzungsquadrate, die entfernt werden müssen?
125
29 J / 29 S
Die Zahl 20{\ast}{\ast}{\ast} 16 ist eine 7-stellige Quadratzahl. Wie lautet der fehlende dreistellige Ziffernblock?
909
30 J / 30 S
Das Dreieck \triangle ABC mit \overline{AB} = \overline{AC} = 5\,\text{m} und \overline{BC} = 6\,\text{m} ist zu einem Teil mit Wasser gefüllt. Liegt das Dreieck auf der Seite BC, so befindet sich die Wasseroberfläche 3\,\text{m} über der Seite BC. Das Dreieck wird nun so gedreht, dass es auf der Seite AB zu liegen kommt. Wie viele Meter befindet sich in diesem Fall die Wasseroberfläche über der Seite AB?
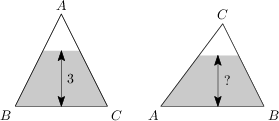
\frac{18}{5}
31 J / 31 S
Gegeben sind sechs Schachteln, die von 1 bis 6 nummeriert sind, und 17 Pfirsiche, die auf unbekannte Weise auf diese Schachteln verteilt sind. Uns ist nur die folgende Vorgehensweise erlaubt: Sind genau n Pfirsiche in der n-ten Schachtel, essen wir einen davon und geben anschließend die verbleibenden n-1 Pfirsiche in die Schachteln 1 bis n-1, und zwar genau einen Pfirsich in jede der Schachteln. Wie müssen die Pfirsiche am Anfang auf die sechs Schachteln verteilt sein, sodass wir alle Pfirsiche essen können?
(1,\,1,\,3,\,2,\,4,\,6)
32 J / 32 S
Ein Zweiersessellift transportiert Touristen berg- und talwärts. Es wollen 74 Personen mit dem Lift auf den Berg fahren und bei der Bergstation warten 26 Personen, die ins Tal fahren möchten. Exakt zu Mittag wird der Sessellift in Betrieb genommen. Zu diesem Zeitpunkt steigen zwei Personen bei der Bergstation und zwei bei der Talstation zu. Die restlichen Personen steigen anschließend jeweils zu zweit und ohne Unterbrechung zu. Um exakt 12:16 Uhr begegnet der erste besetzte nach oben fahrende Zweiersessel dem letzten besetzten talwärts fahrenden Zweiersessel. Um exakt 12:22 Uhr trifft der erste besetzte talwärts fahrende Zweiersessel auf den letzten besetzten nach oben fahrenden Zweiersessel. Die Entfernung zwischen je zwei aufeinander folgenden Sesseln ist stets gleich und die Geschwindigkeit des Sessellifts ist konstant. Wie lange dauert die Fahrt von der Talstation zur Bergstation in Minuten?
26
33 J / 33 S
Gegeben ist eine Raute (ein Rhombus) ABCD mit \angle BAD < \angle ADC. Man wähle einen Punkt M auf der Strecke AB und einen Punkt N auf der Strecke BC, sodass \triangle DMN ein gleichseitiges Dreick ergibt und die Strecken AD und MD gleich lang sind. Die Punkte M und N müssen sich dabei von den Punkten A, B und C unterscheiden. Wie groß ist der Winkel \angle CBA in Grad?
100^\circ
34 J / 34 S
Wie viele Möglichkeiten gibt es, die Zellen einer 2 \times 7–Tabelle mit den Farben Rot und Blau einzufärben, sodass weder ein rotes noch ein blaues L-Trimino in der Tabelle aufscheint?
Jede einzelne Zelle wird vollständig mit einer der beiden Farben ausgefüllt. Ein L-Trimino hat die folgende Form und kann auch in gedrehter Weise vorkommen:

130
35 J / 35 S
Der leidenschaftliche Diamantensammler Manuel besitzt schon eine stattliche Anzahl an Diamanten, allerdings weniger als 200. Er teilt all seine Diamanten folgendermaßen auf mehrere einzelne Haufen, also mindestens zwei, auf:
- Je zwei dieser Haufen bestehen aus einer unterschiedlichen Anzahl von Diamanten.
- Keiner dieser Haufen besteht aus genau zwei Diamanten.
- Für jeden dieser Haufen gilt: Egal wie Manuel ihn in kleinere Haufen unterteilt, so hat mindestens einer der neuen Haufen dieselbe Anzahl an Diamanten, wie sie ein bereits zuvor existierender Haufen hat.
Bestimme unter diesen Voraussetzungen die maximale Gesamtzahl an Diamanten, die Manuel besitzen kann!
Jeder Haufen besteht aus einer von Null verschiedenen Anzahl an Diamanten.
196
36 J / 36 S
Im Spiel Schere-Stein-Papier gibt es die drei Zustände Schere (S), Stein (St), Papier (P) und es gilt S>P, P>St, St>S sowie S=S, St=St, P=P. Wird ein Zustand A gegen einen Zustand B gespielt, so steht die Schreibweise A>B abkürzend für ‚A schlägt B‘ und A=B für ‚Das Spiel endet unentschieden‘. Ein Turnier Schere-Stein-Papier mit zwei Händen ohne Wiederholung zwischen zwei Spielern S_1 und S_2 besteht aus 9 Spielen. In jedem Spiel wählt jeder Spieler ein Paar (\ell_i,r_i), wobei \ell_i und r_i für den gespielten Zustand der linken und der rechten Hand des Spielers S_i steht, und es spielt \ell_1 gegen \ell_2 sowie r_1 gegen r_2. Während des gesamten Wettbewerbs muss jeder Spieler jedes mögliche Paar genau einmal wählen. In einem einzelnen Spiel werden 4 Punkte vergeben: Jeweils 2 Punkte für den Gewinner der linken und 2 Punkte für den Gewinner der rechten Hand, 0 Punkte für den Verlierer und falls unentschieden, 1 Punkt für jeden Spieler pro Hand. Beide Spieler wählen die Reihenfolge ihrer Paare rein zufällig. Wie groß ist die Wahrscheinlichkeit, dass jedes der 9 Spiele aus dem Turnier unentschieden, d. h. mit dem Spielstand 2:2, endet?
3!^3/9!=1/1680
37 J / 37 S
Das Netz eines Körpers besteht aus acht regelmäßigen Dreiecken und sechs Quadraten, wie in der Abbildung zu sehen ist:
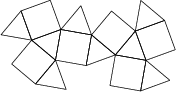
Angenommen die Länge jeder Kante beträgt 1\,\text{km}. Wie groß ist dann das Volumen des Körpers in \text{km}^3?
\frac 53 \sqrt 2
38 J / 38 S
Finde den einzigen dreistelligen Primfaktor von 999\,999\,995\,904.
601
39 J / 39 S
Dreizehn Bienen. Eine kleine Biene und zwölf große Bienen leben in einer 37-zelligen Bienenwabe, wie in der Abbildung zu sehen ist. Jede große Biene besetzt darin drei Zellen, die paarweise benachbart sind, und die kleine Biene genau eine Zelle. Wie viele Möglichkeiten gibt es, die Bienenwabe in dreizehn nicht-überlappende Gebiete aufzuteilen, sodass alle dreizehn Bienen wie oben beschrieben untergebracht werden können?
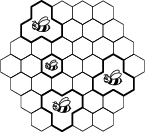
20
40 J / 40 S
Sei \triangle ABC ein gleichseitiges Dreieck und k sein Umkreis. Der Punkt X liege auf dem kürzeren Kreisbogen über der Strecke BC von k und T sei der Schnittpunkt der Geraden AB und CX. Wie lange ist die Strecke BX, falls die Längen \overline{AX} = 5 und \overline{TX} = 3 gegeben sind?
\frac{15}{8}
41 J / 41 S
Sei \triangle ABC ein gleichseitiges Dreieck. Ein innerhalb des Dreiecks \triangle ABC liegender Punkt P wird als strahlend bezeichnet, falls man genau 27 Strahlen finden kann, die von P ausgehen und die Seiten des Dreiecks \triangle ABC so schneiden, dass das Dreieck durch diese Strahlen in 27 flächeninhaltsgleiche kleinere Dreiecke geteilt wird. Bestimme die Anzahl der strahlenden Punkte in \triangle ABC.
\binom{26}{2} = 325
42 J / 42 S
Wie viele positive Teiler von 2016^2 sind kleiner als 2016, aber keine Teiler von 2016?
47
43 J / 43 S
Sei Bestimme z_1 + z_2 + \dots + z_{2016}.
\frac12 (4033\sqrt{4033} - 1)
44 J / 44 S
Eine Folge a_0, a_1, a_2 \dots von ganzen Zahlen sei auf folgende Weise definiert: Wenn a_i durch 3 teilbar ist, ist a_{i+1}=a_i/3, andernfalls ist a_{i+1}=a_i+1. Wie viele verschiedene positive ganze Zahlen a_0 gibt es, so dass die Folge den Wert 1 zum ersten Mal nach exakt 11 Schritten erreicht, das heißt a_{11} = 1 und a_0, a_1, \dots, a_{10} \neq 1?
423
45 J / 45 S
Seien ABCD, AEFG und EDHI Rechtecke mit den zugehörigen Mittelpunkten K, L und J. Weiter seien A auf HI, D auf FG sowie E auf BC jeweils innere Punkte der Strecken und es gelte \angle DEA = 53^\circ. Bestimme die Größe von \angle LKJ (in Grad).
74^\circ
46 J / 46 S
Alexander hat sich mehrfach aus der Menge \{-1, 0, 1, 2\} Zahlen ausgesucht, so dass deren Summe gleich 19 und die Summe ihrer Quadrate gleich 99 ist. Was ist die größtmögliche Summe der dritten Potenzen von Alexanders Zahlen?
133
47 J / 47 S
Finde die größte 9-stellige Zahl mit den folgenden Eigenschaften:
- Alle Ziffern sind verschieden.
- Für jedes k=1,2,\ldots,9 gilt: Wenn die k-te Stelle von links gestrichen wird, ist die resultierende 8-stellige Zahl durch k teilbar.
876\,513\,240
48 J / 48 S
Der Punkt P liegt im Rechteck ABCD mit \overline{AB}=12. In jedem der Dreiecke \triangle ABP, \triangle BCP und \triangle DAP gilt, dass die Maßzahl des Umfangs gleich der Maßzahl der Fläche ist. Wie groß ist der Umfang des Dreiecks \triangle CDP?
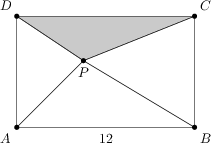
25
49 J / 49 S
Das Paar (0,0) wird an eine Tafel geschrieben. Anschließend wird in jedem Schritt das an der Tafel stehende Paar (a,b) durch das Paar (a+b+c,b+c) ersetzt, wobei die Zahl c in jedem Schritt aus der Menge \{-118, 247\} beliebig gewählt werden darf. Finde die kleinste positive Anzahl von Schritten, nach der das Paar (0,b) an der Tafel erscheinen kann, wobei b irgendeine beliebige Zahl sein darf.
145
50 J / 50 S
Ein ZickZack besteht aus zwei parallelen Strahlen in entgegengesetzter Richtung mit einer geraden Verbindungslinie zwischen den Startpunkten der Strahlen. In wie viele Regionen kann die Ebene mit zehn ZickZacks maximal zerlegt werden?
416
51 J / 51 S
Jede Seite eines Tetraeders ist ein Dreieck mit den Seitenlängen 1, \sqrt 2 und c. Der Umkreisradius des Tetraeders ist 1. Wie groß ist c?
\sqrt 5
52 J / 52 S
Für eine Cocktailparty hat der Butler James 2016 Cocktailgläser mit einem vorzüglichen Kirschcocktail in einer Reihe aufgestellt. Nun deckt er eines dieser Gläser mit einem silbernen Deckel zu und stellt darauf eine Statue. In jedes andere Glas legt er anschließend maximal eine Kirsche. Wie viele derartige Anordnungen von Deckel und Kirschen gibt es, wenn eine ungerade Anzahl an Kirschen verteilt wird und auf der rechten Seite des zugedeckten Glases mehr Kirschen liegen als auf der linken?
2016\cdot 2^{2013}
53 J / 53 S
Die Oberfläche eines Holzwürfels wurde grün angemalt. Insgesamt 33 Ebenen, von denen jede jeweils parallel zwischen zwei gegenüber liegenden Seitenflächen des Würfels liegt, zerschneiden den Würfel in kleine Quader. Bestimme die Gesamtzahl der Quader, in die der Würfel zerschnitten wurde, wenn die Anzahl der Quader mit mindestens einer grünen Seitenfläche genau so groß ist wie die Anzahl der Quader ohne grüne Farbe.
1260 und 1344
54 J / 54 S
Für eine positive ganze Zahl n sei p(n) das Produkt der von Null verschiedenen Ziffern von n. Bestimme den größten Primteiler von p(1)+\dots+p(999).
103
55 J / 55 S
Sei (a_n)_{n\geq 1} eine streng monoton steigende Folge positiver ganzer Zahlen, die für alle positiven ganzen Zahlen k die Bedingungen 9\mid a_{3k-2}, 14\mid a_{3k-1} und 19\mid a_{3k} erfüllt. Bestimme den kleinstmöglichen Wert für a_{2016}.
14\,478
56 J / 56 S
Sei P ein Punkt innerhalb des Dreiecks \triangle ABC. Die Punkte D, E und F liegen jeweils auf den Seiten BC, CA und AB und zwar so, dass sich die Strecken AD, BE und CF im Punkt P schneiden. Bestimme die Fläche des Dreiecks \triangle ABC, wenn die Streckenlängen \overline{PA}=6, \overline{PB}=9, \overline{PD}=6, \overline{PE}=3 und \overline{CF}=20 gegeben sind.
108
57 J / 57 S
Bestimme die letzten zwei Ziffern vor dem Dezimalpunkt der Zahl (7 + \sqrt{44})^{2016}.
05























