1 J
Van egy kocka alakú szikladarabunk, aminek a térfogata 216\,\text{m}^3. Hány négyzetméter lesz a szikla felszíne, miután kivágunk belőle egy 1\,\text{m}\times 1\,\text{m}\times 2\,\text{m} méretű téglatestet az ábrán látható módon?

216
2 J
Két jó barát, Csabi és Jani megnyerték a lottót, és vettek közösen egy 35 \times 25 méteres, téglalap alakú telket. Egy ikerházat akarnak építeni, és egy közös kertet. A G-vel jelölt kert területe 300\, \text{m}^2. Az alaprajz terve az ábrán látható:
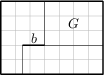
(Két szomszédos rácsvonal távolsága 5\,\text m.) Mennyivel kell a b falnak belógnia az egyik házrészből a másikba, hogy a két barátnak jutó alapterületek egyenlőek legyenek?
8.75\, \text{m}
3 J
A kis Marci le akar menni a strandra. A szekrényében az alábbi a csupa különböző kellékek vannak: 5 úszónadrág, 3 szalmakalap, 4 napszemüveg és 5 póló. Hogy megfeleljen a strandszabályoknak, kötelező fürdőnadrágot felvennie. A szalmakalap, napszemüveg és póló viselése nem kötelező, de ha már felvesz valamit, akkor is csak minden kategóriából legfeljebb egyet. Hányféle megfelelő módon tud Marci megjelenni a strandon?
600
4 J
Laura egy esőerdőbe ment nyaralni. Minden nap vagy délelőtt, vagy délután, vagy egész nap esett az eső. A vakáció alatt 13 olyan napja volt, amikor nem esett egész nap. Összesen 11 esős délelőttöt és 12 esős délutánt élt át. Hány napig tartott Laura vakációja?
18 nap
5 J
Találd meg a legkisebb nemnegatív egész megoldását a következő egyenletnek: n-2\cdot \operatorname{Q}(n)=2016, ahol \operatorname{Q}(n) az n számjegyeinek összege.
2034
6 J
Hány olyan pozitív egész szám van, amelynek az első számjegye megegyezik a számjegyeinek a számával?
111\,111\,111
7 J
Egy felületet sok-sok díszkővel fedtünk le, és ezek közül az egyik szabályos n-szög alakú, amelyet teljesen körbe kerítünk más díszkövekkel. Ha ezt a díszkövet 48^\circ-kal elforgatjuk a középpontja körül, akkor tökéletesen illeszkedik az eredeti pozíciójába. Mennyi a minimális n, amire ez teljesül?
15
8 J
Egy napot boldognak nevezünk, ha a dátumot ÉÉÉÉ.HH.NN formában leírva az 8 különböző számjegyből áll - itt az NN a napot jelöli, a HH a hónapot és az ÉÉÉÉ az évet, és ha a nap vagy a hónap száma 10-nél kisebb, akkor az első számjegy helyére 0-t írunk. Például 1785.04.26 egy boldog nap volt. Mikor lesz a mai naptól számolva a legközelebbi boldog nap?
2345.06.17 azaz 2345. június 17.
9 J
Hány olyan sík van, ami egy adott téglatestnek pontosan négy csúcsát tartalmazza?
12
10 J
Szandra egy gyönyörű félholdat szeretne rajzolni körzővel és vonalzóval. Először rajzol egy M_1 középpontú és r_1=3\ \text{cm} sugarú kört. Aztán beszúrja a körzőt ennek a körnek egy M_2 pontjába, és rajzol egy második kört r_2 sugárral, amely az első kört egy M_1-en átmenő átmérő két átellenes pontjában metszi, ahogy az ábrán látható.
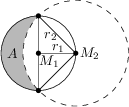
Mi az A-val jelölt félhold területe \text{cm}^2-ben számolva?
9
11 J / 11 S
A Polipkirály minden szolgálójának hat, hét vagy nyolc lába van. A hétlábúak mindig hazudnak, de a hat- vagy nyolclábúak mindig igazat mondanak. Egy napon a Polipkirály magához hívatta négy szolgáját, és megkérdezte tőlük, hogy négyüknek összesen hány lába van. Az első azt állította, hogy a lábak össz-száma 25, a második 26-ot, a harmadik 27-et, a negyedik 28-at mondott. Hány lába van összesen (ezen négy közül) a király igazmondó szolgáinak?
6
12 J / 12 S
Egy bolt tejcsoki, fehér csoki és étcsoki szeleteket árul azonos áron. Egyik nap a bolt 270 értékben adott el tejcsokit, 189-ért fehér csokit és 216-ért étcsokit. Mi lehet a legkisebb értéke az aznap eladott csokiszeletek számának?
25
13 J / 13 S
Egy ötgyermekes apuka süteményeket akar venni a családjának teázáshoz. Sajnos tapasztalatból tudja, hogy ahhoz, hogy elkerülje a gyerekek közti vitát, vagy öt darabot kell szétosztania ugyanabból a fajta süteményből, vagy öt különböző fajta süteményt kell szétosztania. Egy nap, amikor nem tudták eldönteni, hogy milyen süteményt vegyenek, a következő utasítást adta a legkisebb gyermekének: „Menj el a cukrászdába, és kérd meg az eladót, hogy adjon neked x darab süteményt véletlenszerűen! Miután visszajöttél, mindegyik gyerek pontosan egy darab süteményt fog kapni, és a többi darabot megkapja anya és apa!" Feltéve, hogy a cukrászda több mint ötféle süteményt ad el, és mindegyik fajta süteményből bőven van készletük, milyen x számot mondhatott az apa a gyermekének, hogy egyszerre elérje, hogy a gyerekek ne vesszenek össze, és a lehető legkevesebb süteményt kelljen megvásárolniuk?
17
14 J / 14 S
Hogyan aránylik egymáshoz egy olyan kör és négyzet területe, amelyek kerületei megegyeznek?
4 : \pi
15 J / 15 S
Februárban Pali úgy döntött, hogy meglátogatja a Kókusz-szigeteket a magánrepülőgépén. Az európai villájától közép-európai idő (CET) szerint 10:00-kor szállt fel, és a következő nap helyi idő (Kókusz-szigeteki idő, CCT) szerint 5:30-kor szállt le a szigeten. A hazaúton a CCT szerint 8:30-kor szállt fel, és ugyanazon a napon 17:00-kor szállt le a CET szerint. Feltéve, hogy az utazási idő oda és vissza is ugyanannyi volt, mennyi volt az idő a Kókusz-szigeteken, amikor Pali hazaérkezett?
22:30
16 J / 16 S
A 14, 20 és n számok teljesítik a következő tulajdonságot: ha bárhogyan kiválasztunk kettőt közülük és összeszorozzuk, a szorzat osztható lesz a harmadik számmal. Találd meg n összes lehetséges értékét, amire igaz ez a tulajdonság.
70, 140, 280
17 J / 17 S
Egy téglalapot két trapézra osztunk egy x szakasszal a képen látható módon. A PA távolság 10\,\text{cm} és az AQ távolság 8\,\text{cm}. A T_1 trapéz területe 90\,\text{cm}^2 és a T_2 területe 180\,\text{cm}^2.
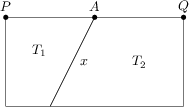
Mekkora az x szakasz hossza \text{cm}-ben?
17
18 J / 18 S
Erzsi epret szed a kertjében. Szét akarja osztani az epret a négy fia között úgy, hogy mindegyik fiú legalább három szemet kapjon, és Aladár többet kapjon, mint Benedek, Benedek többet kapjon, mint Nándor, és Nándor többet kapjon, mint Misi. Mindegyik fiú ismeri a saját epreinek számát, az összes szétosztott eper számát és a fenti feltételeket. Adjunk meg egy szétosztást a négy fiú között úgy, hogy Erzsi a lehető legkevesebb epret ossza ki, teljesüljenek az előbbi feltételek, és egyik fia se tudja meghatározni az összes testvéréről, hogy ki mennyi epret kapott?
(M,\, N,\, B,\, A) = (3,\, 5,\, 6,\, 8)
19 J / 19 S
Felírjuk az összes egész számot 1-től 1000-ig egymás után az óramutató járásával megegyező irányban egy körvonal mentén. Ezután megjelölünk néhány számot: először az 1-est, majd az óramutató járásával megegyezően haladva a kör mentén minden tizenötödik számot megjelölünk (16, 31, és így tovább). Ezt így folytatjuk egészen addig, amíg olyan számot kellene megjelölnünk, amit már korábban megjelöltünk. Összesen hány szám marad jelöletlenül a fenti eljárás elvégzése után?
800
20 J / 20 S
Adjátok meg fokban az ábrán látható hétágú csillag hét jelölt belső szögének az összegét!
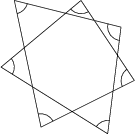
540^\circ
21 J / 21 S
Diákoknak azt a feladatot adták, hogy számolják ki az 1, 3, 6, 7, 8, 10 számok számtani közepét. Luca egy hibás módszerrel próbálta megoldani a feladatot: először kiválasztott kettőt a számok közül, és azoknak vette a számtani közepét. Aztán az így kapott eredménynek és egy, még ki nem választott számnak vette a számtani közepét, és ezt így folytatta, amíg fel nem használta az összes számot. Mi a hiba lehető legnagyobb abszolútértéke (hiba alatt a Luca által kapott eredmény és a helyes megoldás különbségét értjük)?
17/6
22 J / 22 S
Egy egyenes útszakasz egyik oldalán öt jelzőlámpa (L_1, L_2, L_3, L_4, L_5) helyezkedik el sorban 12 méterenként. Az út másik oldalán van egy fagyizó. Ha Géza a fagyizó E-vel jelölt bejáratánál áll, akkor az L_1L_2 szakaszt \alpha=27^\circ szögben látja. Ha az L_5 pontban áll, akkor az L_1E szakaszt szintén 27^\circ szögben látja.
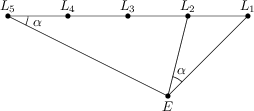
Mekkora az L_1 és E közötti távolság?
24\, \text{m}
23 J / 23 S
Klári 1-től 17-ig kiválasztott két különböző egész számot, és összeszorozta őket. Meglepődve tapasztalta, hogy a szorzat megegyezik a megmaradó tizenöt szám összegével. Add meg azt a két számot, amelyet Klári kiválasztott.
10 és 13
24 J / 24 S
Hány olyan pozitív egész (a, b, c, d, e, f) számhatos van, ami egyszerre elégíti ki az a > b > c > d > e > f és az a+f = b+e = c+d = 30 feltételeket?
\binom{14}{3}=364
25 J / 25 S
Egy időzített bombához egy kijelzőt csatlakoztattak, ami a robbanásig hátralévő időt mutatja percben és másodpercben. A kijelző 50:00-ról kezd el visszaszámolni. Egy villanykörte villan fel minden egyes alkalommal, amikor a kijelzőn a hátralévő percek és a hátralévő másodpercek száma megegyezik (pl. 15:15) vagy amikor a kijelzőn lévő négy számjegy visszafelé olvasva is ugyanaz (pl. 15:51). Akkor hatástalaníthatjuk a bombát, amikor a villanykörte a hetvenedik alkalommal villan fel. Mennyit fog mutatni ekkor a bomba kijelzője?
03:03
26 J / 26 S
Van öt körünk, amelyek az ábrán látható módon érintik egymást. Számítsuk ki a legkisebb kör sugarát, ha a legnagyobb kör sugara 2, és a két másik jelölt középpontú kör sugara 1.
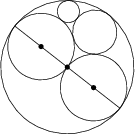
\frac 13
27 J / 27 S
Egy kaszinóban néhányan egy asztalnál ruletteznek. Amikor Erik elhagyta az asztalt, és magával vitte 16\,000 euróját, az asztalnál ülő játékosok átlagos pénzmennyisége 1\,000 euróval csökkent. Az átlag újból csökkent 1\,000 euróval, amikor két másik szerencsejátékos, Betti és Imi csatlakozott az asztalnál ülőkhöz fejenként 2\,000 euróval. Hány játékos ült az asztal körül, amikor Erik még játszott?
9
28 J / 28 S
Egy 7\times7\times7-es kocka bármely két szomszédos kiskockája között van egy elválasztó lapka. El akarunk távolítani az elválasztó lapok közül néhányat úgy, hogy minden egységkocka összeköttetésben legyen legalább egy külső kiskockával. Minimum mennyi elválasztó lapot kell ehhez kivennünk?
125
29 J / 29 S
Tudjuk, hogy 20{\ast}{\ast}{\ast} 16 hétjegyű szám egy egész szám négyzete. Mik a hiányzó számjegyek?
909
30 J / 30 S
Az ABC háromszöget, aminek oldalhosszai AB = AC = 5\,\text{m} és BC = 6\,\text{m}, valameddig megtöltjük vízzel. Amikor a háromszöget a BC oldalára állítjuk, a vízszint 3\,\text{m} magasan van a BC oldal felett. Milyen magasan lesz méterben a vízszint, ha a háromszöget az AB oldalára állítjuk?
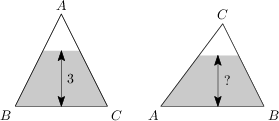
18/5
31 J / 31 S
Van hat dobozunk, amelyeket megszámoztunk 1-től 6-ig és 17 barackunk, amiket valahogy szétosztunk a dobozok között. Egyféle lépésre vagyunk képesek a barackokkal: Ha pontosan n barack van az n-edik dobozban, akkor megeszünk belőlük egyet, és a többi n-1-ből pedig rakunk egyet-egyet a dobozokba 1-től n-1-ig. Hogyan osszuk szét a dobozok közt a barackokat, hogy mindet meg tudjuk enni?
1,1,3,2,4,6
32 J / 32 S
Egy hegyen üzemel egy sílift rögzített, kétszemélyes székekkel. 74 ember szeretne felfele utazni, míg 26 ember várakozik a fenti megállónál. Pontosan délben a lift elindul és mindkét állomáson beül két-két ember a liftbe, ezután a többi várakozó utas folyamatosan tölti fel a rendelkezésre álló helyeket. 12:16-kor az első felfelé haladó szék találkozik az utolsó lefelé haladó foglalt székkel, és 12:22-kor az első lefelé haladó szék találkozik az utolsó felfelé haladó székkel. A távolság két egymást követő szék között mindig ugyanannyi, a lift állandó sebességgel halad, és az utasok mind párokban használják liftet. Milyen hosszú ideig tart eljutni a lenti állomásról a fenti állomásra?
26
33 J / 33 S
Legyen ABCD egy rombusz, az M és N pontok rendre az AB és AC oldalakon fekszenek, és nem esnek egybe az A, B, C csúcsokkal. Tudjuk, hogy DMN szabályos háromszög és AD = MD. Hány fokos az ABC szög?
100^\circ
34 J / 34 S
Hányféleképpen színezhetjük ki egy 2 \times 7-es táblázat celláit a zöld és sárga színekkel úgy, hogy ne legyen se zöld, se sárga L-triminó a táblázatban?
Megjegyzés: L-triminó alatt az ábrán látható alakzatot és az annak elforgatásával kapott alakzatokat értjük.

130
35 J / 35 S
Misi gyémántot gyűjt, de eddig kevesebb, mint 200 gyémántja van. Felosztotta a gyémántjait néhány (legalább kettő) halomba a következő módon:
- bármely két halomban különböző számú gyémánt van,
- semelyik halom sem pontosan két gyémántból áll,
- minden halomra igaz, hogy ha akárhogy szétbontjuk két kisebb halomra, akkor az új halmok közül legalább az egyik pontosan akkora lesz, mint egy, már korábban létező halom (itt a szétbonthatóság kérdésénél nem érvényesek az előző szabályok).
Legfeljebb hány gyémántja lehet Misinek?
196
36 J / 36 S
A kő-papír-ollóban három alakzat közül választhatunk: K –kő, P – papír, O – olló oly módon, hogy O>P, P>K, K>O és K=K, P=P, O=O, ahol A>B azt jelenti, hogy ’A legyőzi B-t’ és A=B azt jelenti, hogy ’amikor A-t játsszuk ki B ellen, a játék döntetlen lesz’. Egy meccs a Kétkezes Ismétlés Nélküli Kő-Papír-Ollóban a P_1 és P_2 játékosok között 9 körből áll. Minden körben mindkét játékos választ egy-egy (b_i,j_i) párt, ahol b_i és j_i rendre a bal és a jobb kéz által kijátszott alakzatot jelölik a P_i játékos részéről. A meccs folyamán mindkét játékosnak pontosan egyszer kell kijátszania minden lehetséges párt. Egy kör során 4 pontot osztunk szét a következő módon: az egyes kézpárok (bal és jobb) győztese 2 pontot kap és a vesztes 0-t, vagy mindkét játékos 1-1 pontot kap, ha az adott pár esetén döntetlen születik. Tegyük fel, hogy a játékosok a körök során véletlenszerűen választják ki, hogy mit akarnak kijátszani. Mekkora a valószínűsége annak, hogy mind a 9 kör a meccs során döntetlennel végződik (azaz 2:2 pontszámokkal)?
3!^3/9!=1/1680
37 J / 37 S
Egy test hálója 8 szabályos háromszögből és 6 négyzetből áll az ábrán látható módon:
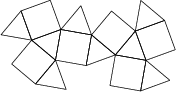
Tegyük fel, hogy minden él hossza 1\,\text{km}, mennyi lesz ekkor a test térfogata (\text{km}^3-ben mérve)?
\frac 53 \sqrt 2
38 J / 38 S
Keressük meg a 999\,999\,995\,904 egyetlen háromjegyű prímtényezőjét.
601
39 J / 39 S
Tizenhárom méh, egy kicsi és tizenkét nagy, egy 37-cellás kaptárban lakik. Minden nagy méh 3 páronként szomszédos cellát foglal el, és a kicsi méh egy cellát foglal el (lásd az ábrát). Hányféleképpen tudjuk a kaptárat felosztani 13 egymást nem fedő részre úgy, hogy mind a tizenhárom méhnek legyen hely a megadott feltételeknek megfelelően?
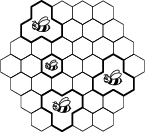
20
40 J / 40 S
Az ABC egyenlő oldalú háromszöget belerajzoljuk az \omega körbe. Az X pont az \omega (rövidebb) BC körívén található, és T az AB és CX szakaszok metszéspontja. Ha AX = 5 és TX = 3, akkor mennyi lesz a BX szakasz hossza?
15/8
41 J / 41 S
Legyen ABC egy szabályos háromszög. Az ABC egy P belső pontját ragyogónak nevezzük ha létezik pontosan 27 P-ből induló félegyenes, amelyek úgy metszik az ABC háromszög oldalait, hogy a háromszöget 27 kisebb, páronként egyenlő területű háromszögre osztják fel. Határozzuk meg ABC ragyogó pontjainak a számát.
\binom{26}{2} = 325
42 J / 42 S
Hány olyan 2016-nál kisebb, pozitív osztója van 2016^2-nek, ami nem osztója 2016-nak?
47
43 J / 43 S
Legyen Számítsuk ki a Z_1 + Z_2 + \dots + Z_{2016} összeget.
\frac12 (4033\sqrt{4033} - 1)
44 J / 44 S
Állítsunk elő egy egészekből álló a_0, a_1, a_2 \dots sorozatot az alábbi módon: Ha a_i osztható hárommal, akkor legyen a_{i+1}=a_i /3, különben pedig a_{i+1}=a_i +1. Hány olyan pozitív egész a_0 létezik, amire a sorozat az 1 értéket pontosan tizenegy lépés alatt éri el (azaz a_{11} = 1, de a_0, a_1, \dots, a_{10} \neq 1)?
423
45 J / 45 S
Legyenek ABCD, AEFG és EDHI téglalapok rendre a K, L, J középpontokkal. Tegyük fel, hogy az A, D, E pontok rendre belső pontjai a HI, FG, BC szakaszoknak, és \angle AED = 53^\circ. Adjuk meg hány fokos a \angle JKL szög.
74^\circ
46 J / 46 S
Jakab választott néhány (nem feltétlenül különböző) egész számot a \{-1, 0, 1, 2\} halmazból, úgy hogy az összegük 19, és a négyzetösszegük (négyzeteik összege) 99. Mi a lehető legnagyobb érték a Jakab által választott számok köbeinek összegére?
133
47 J / 47 S
Keressük meg a legnagyobb 9-jegyű számot az alábbi tulajdonságokkal:
- minden számjegye különböző,
- minden k=1,2,\ldots,9 esetén, ha kitöröljük a szám k-adik számjegyét, a kapott 8 jegyű szám osztható k-val.
876\,513\,240
48 J / 48 S
A P pont az ABCD téglalap belsejében fekszik, és AB=12. Az ABP, BCP, DAP háromszögek mindegyikének a kerülete egyenlő a területével. Mi a CDP háromszög kerülete?
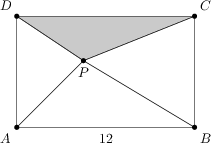
25
49 J / 49 S
A táblára fel van írva a (0,0) számpár. Minden lépésben átírjuk az alábbi módon: Ha (a,b)-van felírva, lecseréljük (a+b+c,b+c)-re, ahol c=247 vagy c=-118 (minden lépésben megválaszthatjuk c értékét) Keressük meg a legkisebb (nem nulla) lépésszámot, amikor (0,b) lesz a táblán valamilyen b-re.
145
50 J / 50 S
Egy cikcakk két párhuzamos, ellentétes irányú félegyenesből, és a kezdőpontjaikat összekötő szakaszból áll. Maximum hány részre oszthatja fel a síkot tíz darab cikcakk?
416
51 J / 51 S
Egy tetraéder minden lapja egy háromszög 1, \sqrt 2 és c hosszú oldalakkal, és a tetraéder köréírt gömbjének sugara 5/6. Mekkora c?
\sqrt{23}/3
52 J / 52 S
Egy nagy ünnepségre Hippolyt, a lakáj felsorakoztatott 2016 koktélpoharat egy sorban, mindben ízletes koktél van. Utolsó simításként le kell takarnia egy poharat egy ezüst fedővel, és rátennie egy szobrot, a lefedetlen poharakba pedig szétoszt páratlan sok cseresznyét, úgy hogy minden pohárba legfeljebb egy cseresznye kerülhet. Hányféleképpen rendezheti el a cseresznyéket és a fedőt, ha több cseresznyének kell lennie a fedő jobb oldalán, mint a bal oldalán?
2016\cdot 2^{2013}
53 J / 53 S
Egy fakockának a felületét zöldre festették. Van 33 sík a térben, mind különbözőek, párhuzamosak a kocka valamelyik lapjával, és valahol a kocka két ellentétes lapja között helyezkednek el. Ezek a síkok kisebb téglatestekre vágják fel a kockát úgy, hogy ugyanannyi darabnak van zöldre festett lapja, mint ahány darab teljesen festetlen. Hány darabra vághattuk fel a kockát?
1260 vagy 1344
54 J / 54 S
Bármely n pozitív egészre legyen p(n) az n nem nulla számjegyeinek szorzata. Számoljuk ki p(1)+\dots+p(999) legnagyobb prímosztóját.
103
55 J / 55 S
Legyen (a_n)_{n=1}^\infty egy pozitív egészekből álló, szigorúan növekvő sorozat, amire 9\mid a_{3k-2}, 14\mid a_{3k-1}, és 19\mid a_{3k} minden k pozitív egészre. Keressük meg a_{2016} lehető legkisebb értékét.
14478
56 J / 56 S
Legyen P egy pont az ABC háromszög belsejében. A D, E, F pontok rendre a BC, CA, AB szakaszokon fekszenek, úgy hogy a AD, BE, CF egyenesek P-ben metszik egymást. Tudjuk, hogy PA=6, PB=9, PD=6, PE=3, és CF=20. Adjuk meg az ABC háromszög területét.
108
57 J / 57 S
Adjuk meg a tizedesvessző előtti utolsó két számjegyét (7 + \sqrt{44})^{2016}-nek.
05