1 J
Dany jest głaz w kształcie sześcianu o objętości 216\,\text{m}^3. Jakie będzie pole powierzchni tego głazu po odłupaniu od niego prostopadłościennego kawałka o wymiarach 1\,\text{m}\times 1\,\text{m}\times 2\,\text{m}, tak jak na poniższym rysunku?

216\,\text{m}^2
2 J
Paweł i Gaweł wygrali w totolotka i zakupili ładną prostokątną działkę budowlaną o wymiarach 35\,\text{m} na 25\,\text{m}. Zamierzają wybudować dwa przylegające do siebie domy i współdzielić ogród G o powierzchni 300\, \text{m}^2. Plan obiektu jest przedstawiony na obrazku:
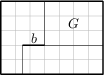
(Odległość między dwiema sąsiednimi liniami siatki wynosi 5\,\text m.) Jak daleko ściana b musi wystawać z jednej części obiektu i zachodzić w drugą część, aby pola powierzchni obu części były równe?
8.75\, \text{m}
3 J
Marek chce wybrać się na plażę. Ma on w swojej szafie następujące (rozróżnialne) stroje: 5 par kąpielówek, 3 kapelusze słomkowe, 4 pary okularów przeciwsłonecznych oraz 5 podkoszulków. Regulamin plaży wymaga założenia kąpielówek, jednak noszenie kapeluszy, okularów przeciwsłonecznych i podkoszulków nie jest obowiązkowe. Wiadomo więc, że Marek założy dokładnie jedne kąpielówki, a także po co najwyżej jednej z pozostałych części stroju. Na ile sposobów Marek może przygotować strój zgodnie z powyższymi warunkami?
600
4 J
Laura spędziła swoje wakacje w lesie deszczowym. Każdego dnia deszcz padał albo tylko rano, albo tylko po południu, albo przez cały dzień. W ciągu wakacji Laury było dokładnie 13 dni, w które nie padało przez cały dzień, dokładnie 11 deszczowych poranków oraz dokładnie 12 deszczowych popołudni. Ile dni trwały wakacje Laury?
18 dni
5 J
Wyznacz najmniejszą nieujemną liczbę całkowitą n taką, że n-2\cdot \operatorname{Q}(n)=2016, gdzie \operatorname{Q}(n) oznacza sumę cyfr liczby n.
2034
6 J
Ile liczb całkowitych dodatnich k ma tę własność, że pierwsza cyfra liczby k jest równa liczbie cyfr liczby k (w zapisie dziesiętnym)?
111\,111\,111
7 J
Chodnik składa się z wielu płytek, z których pewna ma kształt n-kąta foremnego i jest ze wszystkich stron otoczona przez inne płytki. Płytka ta po obrocie wokół swojego środka o 48^\circ przechodzi sama na siebie. Wyznacz minimalne n, dla którego jest to możliwe.
15
8 J
Dzień nazwiemy szczęśliwym, jeżeli jego zapis w formacie DD.MM.RRRR zawiera osiem parami różnych cyfr, gdzie DD oznacza dzień, MM miesiąc, a RRRR — rok oraz dla dni i miesięcy o numerach mniejszych od 10 za pierwszą cyfrę przyjmujemy zero. Przykładowo 26.04.1785 był dniem szczęśliwym. Kiedy nadejdzie najbliższy (licząc od dzisiaj) szczęśliwy dzień?
17.06.2345
9 J
Znajdź liczbę różnych płaszczyzn zawierających dokładnie cztery wierzchołki danego prostopadłościanu.
12
10 J
Mała Kasia chce narysować piękny półksiężyc używając cyrkla i linijki. Najpierw rysuje okrąg o środku w M_1 i promieniu r_1=3\ \text{cm}. Potem wbija cyrkiel w punkt M_2 leżący na tym okręgu i rysuje drugi okrąg o promieniu r_2, który przecina pierwszy okrąg w końcach średnicy przechodzącej przez M_1, tak jak na rysunku poniżej:
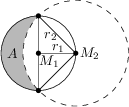
Jakie jest pole półksiężyca A w \text{cm}^2?
9
11 J / 11 S
Każdy ze służących Królowej Ośmiornicy ma sześć, siedem lub osiem nóg. Wszyscy służący mający siedem nóg zawsze kłamią, a wszyscy mający ich sześć lub osiem zawsze mówią prawdę. Pewnego dnia Królowa Ośmiornica przywołała czterech ze swych służących i zapytała ich, ile nóg łącznie ma cała ich czwórka. Pierwszy ze służących odpowiedział, że liczba ta jest równa 25, drugi udzielił odpowiedzi 26, trzeci stwierdził, że 27, a ostatni — że 28. Jaka jest łączna liczba nóg prawdomównych służących Królowej Ośmiornicy (spośród tych czterech)?
6
12 J / 12 S
W pewnym sklepie sprzedawane są tabliczki mlecznej, białej oraz gorzkiej czekolady, wszystkie po tej samej cenie. Pewnego dnia przychód sklepu ze sprzedaży mlecznej czekolady wyniósł 270, ze sprzedaży białej — 189, zaś ze sprzedaży gorzkiej — 216. Jaka jest najmniejsza możliwa liczba tabliczek sprzedanych tego dnia w tym sklepie?
25
13 J / 13 S
Ojciec piątki dzieci chce przygotować ciasteczka na podwieczorek dla pięciorga dzieci. Nauczony bolesnym doświadczeniem wie, że musi rozdać ciasteczka tego samego typu albo wszystkie różne. W przeciwnym razie jego dzieci ciężko się pokłócą. Pewnego dnia po długich dyskusjach o typach ciasteczek, nie mogąc dojść do zgody, zirytowany powiedział do najmłodszej córki Ani: „Pójdziesz do cukierni i poprosisz o x losowo wybranych ciasteczek. Kiedy wrócisz do domu, każde dziecko dostanie ciasteczko, a reszta zostanie dla mamy i taty.” Zakładając, że cukiernia jest zaopatrzona w więcej niż pięć typów ciasteczek, jaką liczbę x wybrał ojciec, by mieć pewność, że będzie mógł rozdać ciasteczka, a jednocześnie zapłacić jak najmniej?
17
14 J / 14 S
Ile wynosi stosunek pola koła do pola kwadratu, jeżeli wiadomo, że ich obwody są równe?
4 : \pi
15 J / 15 S
W lutym Paweł wybrał się na Wyspy Kokosowe (terytorium zależne Australii na Oceanie Indyjskim) swoim prywatnym odrzutowcem. Wystartował ze swojej posesji w Europie o 10:00 czasu środkowoeuropejskiego (CET), a wylądował na wyspach następnego dnia o 5:30 czasu lokalnego (CCT). Wracając do domu wystartował o 8:30 czasu lokalnego (CCT), a wylądował o 17:00 czasu środkowoeuropejskiego (CET), tego samego dnia. Zakładając, że oba loty trwały tak samo długo, która godzina była na Wyspach Kokosowych, gdy Paweł lądował w domu?
22:30
16 J / 16 S
Liczby 14, 20 oraz n spełniają następujący warunek: Iloczyn dowolnych dwóch z nich jest podzielny przez trzecią. Wyznacz wszystkie liczby całkowite dodatnie n, dla których powyższy warunek jest spełniony.
70, 140, 280
17 J / 17 S
Prostokąt jest podzielony na dwa trapezy wzdłuż odcinka o długości x, tak jak pokazano na rysunku. Długości odcinków PA i AQ wynoszą odpowiednio 10\,\text{cm} i 8\,\text{cm}. Pole trapezu T_{1} jest równe 90\,\text{cm}^2, natomiast pole trapezu T_{2} wynosi 180\,\text{cm}^2.
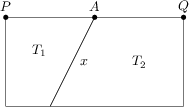
Ile wynosi długość odcinka x w \text{cm}?
17
18 J / 18 S
Elżbieta zebrała truskawki z ogródka. Chce teraz rozdać część z nich swoim czterem synom w taki sposób, by każdy z nich otrzymał co najmniej trzy owoce, a ponadto Dominik dostał ich więcej od Czesława, Czesław od Bartka, a Bartek od Adama. Po rozdaniu truskawek, każdy z synów wie, ile sam ich dostał, ile w sumie truskawek zostało rozdanych, a także zna przedstawione powyżej warunki. W jaki sposób Elżbieta powinna rozdać owoce, aby oddać ich jak najmniej, a także by żaden z synów nie mógł ze stuprocentową pewnością ustalić, ile truskawek dostał każdy z nich?
(A,\, B,\, C,\, D) = (3,\, 5,\, 6,\, 8)
19 J / 19 S
Na okręgu napisane są, zgodnie z ruchem wskazówek zegara, kolejne liczby całkowite od 1 do 1000. Począwszy od 1, zaznaczamy co piętnastą napisaną liczbę idąc zgodnie z ruchem wskazówek zegara (tzn. 1, 16, 31, itd.). Postępujemy tak aż do momentu, kiedy będziemy musieli zaznaczyć liczbę, która już była zaznaczona. Jak wiele liczb pozostanie niezaznaczonych po wykonaniu tej procedury?
800
20 J / 20 S
Wyznacz sumę miar siedmiu kątów zaznaczonych na poniższym rysunku (w stopniach).
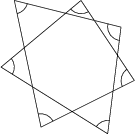
540^\circ
21 J / 21 S
Uczniowie pewnej klasy jako zadanie domowe mieli policzyć średnią arytmetyczną liczb 1, 3, 6, 7, 8 i 10. Niestety, Lucyna zastosowała niepoprawną metodę jego rozwiązania: najpierw wybrała dwie spośród danych liczb i policzyła ich średnią arytmetyczną. Następnie policzyła średnią z tej średniej i którejś z pozostałych liczb i powtarzała ten krok, aż użyte zostały wszystkie spośród początkowych liczb. Jaki jest największy błąd bezwzględny (tzn. wartość bezwzględna różnicy uzyskanego i poprawnego wyniku), jaki mogła otrzymać?
17/6
22 J / 22 S
Po jednej stronie prostej ulicy znajduje się pięć latarni L_1, L_2, L_3, L_4 i L_5 w równych dwunastometrowych odstępach. Po przeciwnej stronie stoi sklep z lodami. Wejście do sklepu oznaczone jest punktem E. Kąt trójkąta EL_1L_2 leżący naprzeciw boku L_1L_2 ma miarę \alpha=27^\circ. Kąt trójkąta EL_1L_5 leżący naprzeciw EL_1 ma taką samą miarę \alpha=27^\circ.
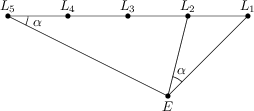
Ile wynosi odległość od L_1 do E?
24\, \text{m}
23 J / 23 S
Klara wylosowała dwie różne liczby naturalne spośród liczb od 1 do 17 (włącznie), a następnie pomnożyła je. Niespodziewanie, otrzymany iloczyn okazał się być równy sumie pozostałych piętnastu liczb. Znajdź dwie liczby, które wylosowała Klara.
10 i 13
24 J / 24 S
Wyznacz ile jest szóstek (a, b, c, d, e, f) liczb całkowitych dodatnich takich, że a > b > c > d > e > f oraz a+f = b+e = c+d = 30?
\binom{14}{3}=364
25 J / 25 S
Bomba zegarowa jest wyposażona w wyświetlacz elektroniczny pokazujący czas do wybuchu w minutach i sekundach. Odliczanie rozpoczęło się od wartości 50:00 na wyświetlaczu. Światełko zapala się, gdy na wyświetlaczu liczba minut jest równa liczbie sekund (np. 15:15) lub gdy możemy czytać cyfry w odwróconej kolejności nie zmieniając wyniku (np. 15:51). Możemy rozbroić bombę w momencie, gdy światełko zapali się po raz 70. Jaki czas będzie wtedy pokazywał wyświetlacz?
03:03
26 J / 26 S
Danych jest pięć stycznych okręgów jak pokazano na rysunku. Znajdź promień najmniejszego okręgu, jeśli promień największego okręgu wynosi 2, natomiast promienie dwóch okręgów z zaznaczonymi środkami są równe 1.
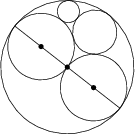
\frac 13
27 J / 27 S
W kasynie, przy jednym z wielkich stołów, toczy się gra w ruletkę. Gdy Eryk opuścił grę z żetonami wartymi 16\,000 euro, średni majątek przy tym stole zmalał o 1\,000 euro. Gdy jakiś czas później do stołu dołączyły hazardzistki Ola i Jola, każda z majątkiem wartym 2\,000 euro, ponownie przeciętny wynik przy stole spadł o 1\,000 euro. Ilu graczy siedziało przy stole zanim Eryk opuścił grę?
9
28 J / 28 S
W sześcianie 7\times7\times7 każde dwa sąsiadujące ze sobą jednostkowe sześciany są oddzielone od siebie przegrodą. Chcemy usunąć pewną liczbę przegród, tak aby każdy jednostkowy sześcian został połączony z co najmniej jednym zewnętrznym sześcianem jednostkowym. Jaka jest najmniejsza liczba przegród, które trzeba usunąć?
125
29 J / 29 S
Wiadomo, że 20{\ast}{\ast}{\ast} 16 jest siedmiocyfrowym kwadratem pewnej liczby naturalnej. Jakie trzy cyfry zostały pominięte?
909
30 J / 30 S
Trójkąt ABC, w którym AB = AC = 5\,\text{m} oraz BC = 6\,\text{m}, jest częściowo wypełniony wodą. Gdy trójkąt leży na boku BC, poziom powierzchni wody znajduje się 3\,\text{m} ponad bokiem. Na jakiej wysokości w metrach znajduje się powierzchnia wody, gdy trójkąt leży na boku AB?
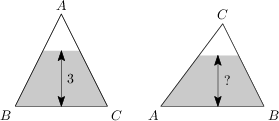
18/5
31 J / 31 S
Mamy 6 pudełek ponumerowanych od 1 do 6, w których umieszczono łącznie 17 brzoskwiń. Możemy wykonywać ruchy zgodnie z następującą zasadą: Jeśli jest dokładnie n brzoskwiń w pudełku o numerze n, to możemy zjeść jedną brzoskwinię, a pozostałe n-1 rozłożyć po jednej w pudełkach od 1 do n-1. Jak rozmieszczono 17 brzoskwiń, aby możliwe było zjedzenie wszystkich zgodnie z powyższą zasadą?
1, 1, 3, 2, 4, 6
32 J / 32 S
Prosty wyciąg krzesełkowy z dwuosobowymi siedzeniami pracuje na stoku. 74 osoby planują wjazd na górę, podczas gdy 26 osób czeka u góry, aby zjechać w dół. Dokładnie w południe para osób siada na krzesełko na obu przystankach. Następnie pozostali pasażerowie kolejno siadają na kolejne krzesełka. o 12:16 pierwsze krzesełko jadących do góry mija ostatnie zapełnione krzesełko podróżujących w dół, a o 12:22 pierwsze krzesełko jadących w dół mija ostatnie zajęte krzesełko jadących w górę. Odległość pomiędzy każdymi dwoma krzesełkami jest taka sama, a wyciąg pracuje ze stałą szybkością oraz wszyscy pasażerowie jadą parami. Jak długo trwa podróż z dolnego przystanku wyciągu do góry (w minutach)?
26
33 J / 33 S
W rombie ABCD punkty M i N różne od punktów A, B i C leżą na odcinkach odpowiednio AB, BC tak, że trójkąt DMN jest równoboczny oraz AD = MD. Znajdź \angle ABC (w stopniach).
100^\circ
34 J / 34 S
Każde pole szachownicy 2 \times 7 kolorujemy na żółto lub zielono. Ile jest możliwych kolorowań szachownicy takich, że na szachownicy nie występuje żółty lub zielony L-trimino?
L-trimino jest poniższym (lub obróconym) kształtem:

130
35 J / 35 S
Michał jest zapalonym zbieraczem diamentów, ale na razie posiada ich mniej niż 200. Podzielił je na kilka stosów (przynajmniej dwa), w taki sposób, że:
- każde dwa stosy składają się z różnej liczby diamentów,
- w żadnym stosie nie ma dokładnie dwóch diamentów,
- jeśli którykolwiek stos podzielimy na dwa mniejsze, to przynajmniej jeden z nich będzie zawierał tyle samo diamentów, co już istniejący.
Jaka jest największa liczba diamentów, które może posiadać Michał?
Stos składa się z niezerowej liczby diamentów.
196
36 J / 36 S
W grze w „papier, kamień, nożyce” można pokazać trzy symbole: P — papier, K — kamień oraz N — nożyce, które są powiązane zależnościami N>P, P>K, K>N oraz K=K, P=P, N=N, przy czym A>B oznacza „A pokonuje B”, zaś A=B oznacza „gdy A i B są grane przeciwko sobie, runda kończy się remisem”. Turniej Dwuręcznego Marynarza Bez Powtórzeń między graczami G_1 i G_2 składa się z 9 rund opisanych powyżej. W każdej rundzie każdy z graczy wybiera parę (\ell_i,p_i), gdzie \ell_i oraz p_i oznaczają odpowiednio symbole pokazane przez lewą oraz prawą dłoń gracza G_i. Podczas całego turnieju każdy z graczy musi wybrać każdą z możliwych par dokładnie raz. W każdej rundzie między graczy rozdzielane są dokładnie 4 punkty w następujący sposób: dla każdej pary grających ze sobą dłoni (lewe/prawe) zwycięzca dostaje 2 punkty a przegrany 0 punktów lub obaj gracze dostają po jednym punkcie jeśli jest remis (na danej parze dłoni). Przypuśćmy, że gracze wykonują ruchy losowo. Jakie jest prawdopodobieństwo, że każda z 9 rund turnieju zakończy się remisem (tzn. z wynikiem 2:2)?
3!^3/9!=1/1680
37 J / 37 S
Dana jest bryła, której siatka zawiera osiem trójkątów równobocznych i sześć kwadratów, tak jak na poniższym rysunku:
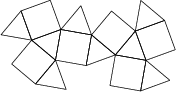
Zakładając, że długość każdej z krawędzi wynosi 1\,\text{km}, jaka jest objętość bryły (w \text{km}^3)?
\frac 53 \sqrt 2
38 J / 38 S
Znajdź jedyny trzycyfrowy dzielnik pierwszy liczby 999\,999\,995\,904.
601
39 J / 39 S
Trzynaście pszczół: pszczółka Maja i dwanaście dużych pszczół mieszka w plastrze miodu składającym się z 37 komórek. Każda duża pszczoła zajmuje trzy parami sąsiednie komórki, a Maja zajmuje dokładnie jedną komórkę (tak, jak na rysunku). Na ile sposobów możemy podzielić plaster miodu na 13 rozłącznych części, tak żeby każda pszczoła zajęła dokładnie jedną część?
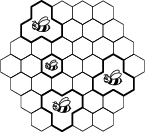
20
40 J / 40 S
Trójkąt równoboczny ABC jest wpisany w okrąg \omega. Punkt X leży na krótszym łuku BC okręgu \omega, proste AB i CX przecinają się w punkcie T. Ile wynosi długość odcinka BX, jeśli AX = 5 oraz TX = 3?
15/8
41 J / 41 S
Niech ABC będzie trójkątem równobocznym. Punkt P leżący we wnętrzu trójkąta ABC nazywamy błyszczącym, jeśli możemy znaleźć 27 półprostych o początku w P przecinających boki trójkąta ABC tak, że ten trójkąt będzie podzielony przez te półproste na 27 mniejszych trójkątów o równym polu. Wyznacz liczbę błyszczących punktów wewnątrz trójkąta ABC.
\binom{26}{2} = 325
42 J / 42 S
Ile jest dodatnich dzielników 2016^2 mniejszych od 2016, które nie są dzielnikami 2016?
47
43 J / 43 S
Niech Oblicz Z_1 + Z_2 + \dots + Z_{2016}.
\frac12 (4033\sqrt{4033} - 1)
44 J / 44 S
Ciąg liczb całkowitych a_0, a_1, a_2, \dots konstruujemy zgodnie z zasadą: Jeśli a_i jest podzielne przez 3, to a_{i+1}=a_i /3, w przeciwnym wypadku a_{i+1}= a_i +1. Dla ilu całkowitych dodatnich wyrazów początkowych a_0 ciąg osiąga wartość 1 pierwszy raz dokładnie po 11 krokach (tj. a_{11}=1, ale a_0, a_1, \ldots, a_{10} \neq 1)?
423
45 J / 45 S
Niech ABCD, AEFG i EDHI będą prostokątami, których środkami są odpowiednio punkty K, L, J. Załóżmy, że A leży na HI, D leży na FG, E leży na BC oraz \angle AED = 53^\circ. Podaj miarę \angle JKL (w stopniach).
74^\circ
46 J / 46 S
Jakub wybrał pewną liczbę (niekoniecznie różnych) liczb pochodzących ze zbioru \{-1, 0, 1, 2\} w taki sposób, że ich suma jest równa 19, a suma ich kwadratów jest równa 99. Jaka jest największa możliwa wartość sumy sześcianów liczb wybranych przez Jakuba?
133
47 J / 47 S
Podaj największą liczbę dziewięciocyfrową taką, że
- wszystkie jej cyfry są różne
- dla k=1,2,\ldots, 9, jeśli wykreślimy k-tą cyfrę, to otrzymamy liczbę ośmiocyfrową podzielną przez k.
876\,513\,240
48 J / 48 S
Punkt P leży wewnątrz prostokąta ABCD w którym AB=12. Każdy z trójkątów ABP, BCP, DAP ma obwód równy swojemu polu. Ile wynosi obwód trójkąta CDP?
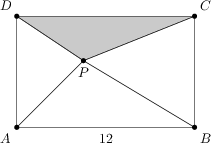
25
49 J / 49 S
Para (0,0) jest napisana na tablicy. W każdym kroku zamieniamy ją w następujący sposób: Pozostałą na tablicy parę (a,b) zamieniamy na (a+b+c,b+c), gdzie c=247 lub c=-118 (możemy wybrać c w każdym kroku). Wyznacz najmniejszą niezerową liczbę kroków po których na tablicy zostanie para postaci (0,b) dla pewnej liczby całkowitej b.
145
50 J / 50 S
Zygzak składa się z dwóch równoległych półprostych o przeciwnych zwrotach i odcinka łączącego ich początki. Na ile maksymalnie części może podzielić płaszczyznę dziesięć zygzaków?
416
51 J / 51 S
Każda ze ścian pewnego czworościanu jest trójkątem o bokach długości 1, \sqrt 2 oraz c, zaś promień sfery opisanej na tym czworościanie jest równy 1. Znajdź c.
\sqrt 5
52 J / 52 S
Przygotowując wielkie przyjęcie powitalne, kamerdyner Jarek ustawił w rzędzie 2016 kieliszków koktajlowych, z których każdy zawiera przepyszny koktajl wiśniowy. Aby zakończyć przygotowania, Jarek musi jeszcze przykryć jeden z kieliszków srebrnym wieczkiem przyozdobionym statuetką, a następnie rozdzielić nieparzystą liczbę wisienek do nieprzykrytych kieliszków, w każdym umieszczając co najwyżej jedną. Ile jest możliwych rozmieszczeń wieczka oraz wisienek, jeżeli po prawej stronie kieliszka z wieczkiem ma być w sumie więcej wisienek niż po jego lewej stronie?
2016\cdot 2^{2013}
53 J / 53 S
Powierzchnia drewnianego sześcianu jest pomalowana na zielono. Dane są 33 różne płaszczyzny, z których każda położona jest między dwiema przeciwległymi ścianami sześcianu i do nich równoległa, które rozcinają sześcian na małe prostopadłościenne klocki. Wiedząc, że liczba klocków z co najmniej jedną ścianą zieloną jest równa liczbie klocków bez żadnej zielonej ściany, znajdź łączną liczbę klocków, na które podzielony jest sześcian.
1260 lub 1344
54 J / 54 S
Dla dowolnej liczby całkowitej dodatniej n, niech p(n) oznacza iloczyn jej niezerowych cyfr. Wyznacz największy dzielnik pierwszy liczby p(1)+\dots+p(999).
103
55 J / 55 S
Niech (a_n)_{n=1}^\infty będzie ściśle rosnącym ciągiem liczb całkowitych dodatnich takim, że 9\mid a_{3k-2}, 14\mid a_{3k-1} oraz 19\mid a_{3k} dla wszystkich liczb całkowitych dodatnich k. Znajdź najmniejszą możliwą wartość a_{2016}.
14478
56 J / 56 S
Niech P będzie punktem wewnątrz trójkąta ABC. Punkty D, E, F leżą odpowiednio na odcinkach BC, CA, AB tak, że proste AD, BE, CF przecinają się w P. Znajdź pole trójkąta ABC, jeśli PA=6, PB=9, PD=6, PE=3 i CF=20.
108
57 J / 57 S
Wyznacz ostatnie dwie cyfry przed przecinkiem liczby (7 + \sqrt{44})^{2016}.
05