1 J
Majme balvan v tvare kocky s objemom 216\,\text{m}^3. Aký je povrch balvana v \text{m}^2 potom, čo z neho vysekneme blok s rozmermi 1\,\text{m}\times 1\,\text{m}\times 2\,\text{m} tak, ako je zobrazené na obrázku?

216
2 J
Dvaja priatelia, Peťo a Tomáš, vyhrali jackpot a kúpili si krásny obdĺžnikový pozemok s rozmermi 35\,\text{m}\times 25\,\text{m}. Chceli na ňom postaviť dvojdom a mať pri ňom spoločnú záhradu G s rozlohou 300\, \text{m}^2. Pôdorys záhrady a domov je na obrázku. (Vzdialenosť medzi dvomi susednými čiarami siete, v ktorej je zakreslený pôdorys záhrady a domov je 5\,\text m).
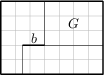
Aká dlhá musí byť stena b z jedného domu do druhého aby plochy domov boli rovnaké?
8.75\, \text{m}
3 J
Malá Janka chce ísť na pláž. K dispozícií má nasledovné rozlíšiteľné plážové outfity: 5 plaviek, 3 slamené klobúky, 4 slnečné okuliare a 5 tričiek. V súlade s pravidlami pláže, musí mať na sebe plavky. Nosenie slnečných okuliarov, klobúka a trička nie je povinné. Avšak na sebe môže mať najviac jeden kus z každého. Koľko je rôznych outfitov, v ktorých Janka môže vyjsť na pláž?
600
4 J
Katka strávila dovolenku v dažďovom pralese. Každý deň buď pršalo iba dopoludnia, iba popoludní, alebo pršalo celý deň. Katka mala počas dovolenky 13 dní, keď nepršalo po celý deň. Počas 11 dní pršalo dopoludnia a 12 dní pršalo popoludní. Ako dlho bola Katka na dovolenke?
18 dní
5 J
Nájdite najmenšie nezáporné celočíselné riešenie rovnice n-2\cdot \operatorname{Q}(n)=2016, kde \operatorname{Q}(n) označuje ciferný súčet čísla n.
2034
6 J
Koľko kladných celých čísel má vlastnosť, že jeho prvá cifra (zľava) je rovná počtu cifier daného čísla?
111\,111\,111
7 J
Dlažba sa skladá z dlaždíc rôznych tvarov, z ktorých jedna má tvar pravidelného n-uholníka. Ak túto dlaždicu vytiahneme a otočíme o 48^\circ okolo jej stredu, tak zapasuje presne na pôvodné miesto. Aké je najmenšie n, pre ktoré je to možné?
15
8 J
Deň nazývame šťastný, ak jeho dátum v tvare DD.MM.RRRR (DD označuje deň, MM označuje mesiac a RRRR označuje rok) pozostáva z ôsmych rôznych číslic. Ak je deň alebo mesiac číslo menšie ako 10, doplní sa nulou na dvojciferné číslo. Napríklad 26.04.1785 bol šťastný deň. Kedy najbližšie, od dnes, bude šťastný deň?
17.06.2345
9 J
Koľko rôznych rovín obsahuje práve štyri vrcholy daného kvádra?
12
10 J
Malá Sandra chce nakresliť prekrásny polmesiac len pomocou pravítka a kružidla. Najprv nakreslí kruh so stredom M_1 a polomerom r_1=3\ \text{cm}. Potom zapichne kružidlo do bodu M_2 na obvode kruhu a nakreslí druhý kruh s polomerom r_2, ktorý pretína prvý kruh v protiľahlých bodoch. Úsečka spájajúca tieto body je priemerom prvého kruhu cez bod M_1, ako je zobrazené na obrázku.
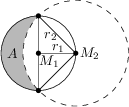
Aký obsah má polmesiac A v \text{cm}^2?
9
11 J / 11 S
Sluhovia kráľa Chobotnicu majú šesť, sedem, alebo osem chápadiel. Tí, ktorí majú sedem chápadiel vždy klamú, zatiaľ čo tí, ktorí majú šesť alebo osem chápadiel vždy vravia pravdu. Jedného dňa kráľ Chobotnica zavolal štyroch svojich sluhov a spýtal sa ich, koľko chápadiel majú oni štyria spolu. Prvý sluha odpovedal, že celkovo majú spolu 25, ďalší tvrdil 26, tretí povedal 27 a posledný vyhlásil, že 28. Koľko chápadiel majú kráľovi pravdovravní sluhovia (z týchto štyroch) dokopy?
6
12 J / 12 S
V obchode predávajú tabuľky mliečnej, bielej a tmavej čokolády za rovnakú cenu. Jeden deň v obchode zarobili 270 eur za predaj mliečnej čokolády, 189 eur za predaj bielej čokolády a 216 eur za predaj tmavej čokolády. Aké najmenšie množstvo tabuliek čokolády mohli v danom obchode v ten deň predať?
25
13 J / 13 S
Otec piatich detí chce kúpiť pečivo pre svoju rodinu na čajový večierok. Po zlých skúsenostiach vie, že potrebuje pre svoje deti buď päť rovnakých, alebo päť rôznych druhov pečiva. Jedného dňa povedal svojej najmladšej dcére Anne: „Choď do cukrárne a od predavačky si pýtaj $x$ náhodných kúskov pečiva! Po tvojom návrate domov, dostane každé dieťa jeden kus pečiva a zvyšné kusy budú pre mamu a otca.“ Za predpokladu, že obchod predáva viac ako päť druhov pečiva a je vždy dobre zásobené každým druhom pečiva, aké číslo x musí otec zvoliť, aby medzi deťmi zaručene nevznikli hádky kvôli pečivu a zároveň kúpil čo najmenej pečiva?
17
14 J / 14 S
Určte pomer obsahu kruhu k obsahu štvorca, ak ich obvody majú rovnakú dĺžku.
4 : \pi
15 J / 15 S
Vo Februári sa Paľo rozhodol navštíviť Kokosové ostrovy svojou súkromnou stíhačkou. Vzlietol od svojho sídla v Európe o 10.00 stredoeurópskeho času (SEČ) a pristál na Kokosových ostrovoch nasledujúci deň o 5.30 miestneho času (CCT). Keď sa vracal domov, vzlietol o 8.30 CCT a pristál v Európe o 17.00 SEČ ten istý deň. Oba lety trvali Paľovi rovnako dlho. Aký bol čas na kokosových ostrovoch, keď sa Paľo vrátil domov?
22.30
16 J / 16 S
Čísla 14, 20 a n spĺňajú nasledovnú podmienku: Keď vynásobíme ľubovoľné dve z nich, výsledok je deliteľný tretím číslom. Nájdite všetky kladné celé čísla n, pre ktoré je splnená uvedená podmienka.
70, 140, 280
17 J / 17 S
Obdĺžnik je rozdelený na dva lichobežníky deliacou čiarou x ako na obrázku. Vzdialenosť PA je 10\,\text{cm} a AQ je 8\,\text{cm}. Obsah lichobežníka T_1 je 90\,\text{cm}^2 a obsah lichobežníka T_2 je 180\,\text{cm}^2.
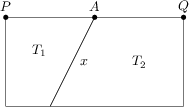
Aká je dĺžka deliacej čiary x v \text{cm}?
17
18 J / 18 S
Betka zbierala jahody vo svojej záhradke. Chcela ich rozdeliť medzi svojich štyroch synov tak, že každý dostane aspoň 3 jahody a Vlado dostane viac ako Bohuš, Bohuš dostane viac ako Fero a Fero dostane viac ako Marek. Každý zo synov vie svoj počet jahôd, celkový počet jahôd ktoré sa delili a vyššie spomínané podmienky rozdelenia jahôd. Ako môže Betka rozdeliť jahody za predpokladu, že chce rozdeliť čo najmenej jahôd a žiaden zo synov nemá vedieť celé rozdelenie ako Betka jahody delila?
(M,\, F,\, B,\, V) = (3,\, 5,\, 6,\, 8)
19 J / 19 S
Postupne v smere hodinových ručičiek pozdĺž obvodu kruhu napíšeme všetky celé čísla od 1 do 1\,000 Potom označíme niekoľko čísel: Začneme číslom 1 a následne v smere hodinových ručičiek označíme každé 15-te číslo (t. j. 16, 31 atď.). Týmto spôsobom označujeme čísla dovtedy, kým nie sme nútení označiť číslo, ktoré sme už označili. Koľko čísel ostane neoznačených po tomto procese?
800
20 J / 20 S
Nájdite súčet siedmych vyznačených vnútorných uhlov tejto 7-cípej hviezdy (v stupňoch)!
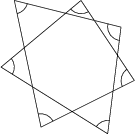
540^\circ
21 J / 21 S
Žiaci dostali nasledujúcu úlohu. Mali spočítať aritmetický priemer čísel 1, 3, 6, 7, 8 a 10. Avšak Lucia zvolila zlý postup: Najprv zobrala dve čísla a vypočítala ich aritmetický priemer. Potom zobrala výsledok a ďalšie z čísel a vypočítala ich aritmetický priemer. Takto postupovala kým nepoužila všetky čísla. Čisla pritom brala v ľubovoľnom poradí. Aká je najväčšia hodnota chyby (t.j. rozdiel medzi výsledkom ktorý dostala Lucia a správnym výsledkom) ktorý Lucia mohla dostať?
17/6
22 J / 22 S
Pozdĺž jednej strany cesty je päť pouličných lámp L_1, L_2, L_3, L_4, a L_5 ležiacich na priamke a rovnomerne rozmiestnených každých 12\, {\rm m}. Na druhej strane cesty je obchod so zmrzlinou. Ak Júlia stojí pred vchodom E zmrzlinového obchodu, vidí z tohto bodu lampy L_1 a L_2 pod uhlom \alpha=27^\circ. Ak stojí pri lampe L_5, vidí lampu L_1 a vchod E tiež pod uhlom 27^\circ.
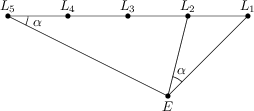
Aká je vzdialenosť od lampy L_1 k vchodu E?
24\, \text{m}
23 J / 23 S
Dominika si vybrala dve prirodzené čísla z čísel od 1 to 17 (zahŕňajúce aj 1 a 17) a vynásobila ich. Na prekvapenie, výsledok ktorý dostala bol rovný súčtu zvyšných 15-tich čísel. Aké dve čísla si Dominika vybrala?
10 a 13
24 J / 24 S
Koľko rôznych 6-tíc (a, b, c, d, e, f) kladných celých čísel spĺňa podmienky a > b > c > d > e > f a zároveň a+f = b+e = c+d = 30?
\binom{14}{3}=364
25 J / 25 S
Časovaná bomba je vybavená displejom zobrazujúcim čas pred výbuchom v minútach a sekundách. Odpočítavanie začne na čase 50:00. Žiarovka blikne, ak počet zostávajúcich minút sa rovná počtu zostávajúcich sekúnd zobrazených na displeji (napr. 15:15), alebo keď sa štyri číslice zobrazené na displeji dajú prečítať rovnako odpredu i odzadu (napr. čas 15:51). Bombu môžeme zneškodniť keď žiarovka blikne po 70. raz. Aký čas bude na displeji bomby v tej chvíli?
03:03
26 J / 26 S
Päť kružníc sa vzájomne dotýka tak ako je znázornené na obrázku. Nájdite polomer najmenšej kružnice ak polomer najväčšej kružnice je 2 a zvyšné dve kružnice s vyznačenými stredmi majú polomer 1.
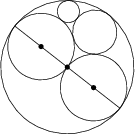
\frac 13
27 J / 27 S
V kasíne sedí niekoľko ľudí okolo veľkého stola a hrá ruletu. Keď Matúš opustí stôl, odnáša si výhru vo výške 16 \ 000 a priemerný zostatok zvyšných hráčov, ktorí ostanú pri stole, sa zníži o 1 000 eur. Znovu sa zníži o 1 000 eur, keď sa pridajú do hry dvaja hráči Rišo a Dorka, každý so vstupným vkladom po 2 000 eur. Koľko hráčov sedelo okolo stola, pokiaľ pri ňom sedel aj Matúš?
9
28 J / 28 S
V kocke 7\times7\times7, sú každé dve susedné jednotkové kocky oddelené zatvorenými dverami. Chceme otvoriť niekoľko dvier tak, aby sa z každej jednotkovej kocky dalo dostať do aspoň jednej vonkajšej jednotkovej kocky. Aký najmenší počet dverí musíme otvoriť?
125
29 J / 29 S
Je známe, že 20{\ast}{\ast}{\ast} 16 je 7-ciferná druhá mocnina prirodzeného čísla. Aké tri cifry majú byť namiesto hviezdičiek?
909
30 J / 30 S
Trojuholník ABC s |AB| = |AC| = 5\,\text{m} a BC = 6\,\text{m} je čiastočne naplnený vodou. Keď trojuholník leží na strane BC, voda siaha do výšky 3\,\text{m}. Do akej výšky siaha voda ak trojuholník leží na strane AB?
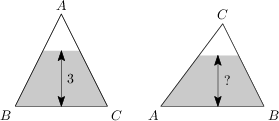
18/5
31 J / 31 S
Majme šesť škatuliek očíslovaných od 1 do 6 a 17 broskýň rozdelených nejako v týchto škatuľkách. V jednom ťahu smieme urobiť nasledovné: Ak sa v n-tej krabici nachádza práve n broskýň, zjeme jednu z nich a zvyšných n-1 broskýň rozdelíme po jednej do krabíc 1 až n-1. Aké je rozloženie broskýň za predpokladu, že vieme postupne zjesť všetky broskyne?
1, 1, 3, 2, 4, 6
32 J / 32 S
V lyžiarskom stredisku je prevádzkovaný dvojmiestny lyžiarsky vlek. Cestu hore na svah na ňom plánuje 74 ľudí, zatiaľ čo 26 cestujúcich čaká už v hornej stanici na cestu dole. Na poludnie začne vlek premávať a nasadne doň v oboch staniciach prvá dvojica ľudí. Ďalší postupne nastupujú. O 12.16 ľudia sediaci na prvých sedadlách smerom hore míňajú posledné obsadené sedadlá, ktoré šli dole. O 12.22, ľudia na prvých obsadených sedadlách, ktoré šli smerom dole míňajú posledné obsadené sedadlá ktoré idú smerom hore. Vzdialenosť medzi každými dvoma dvojsedadlami na lanovke je rovnaká a lanovka udržuje konštantnú rýchlosť. Obsadené sú vždy obe sedadlá. Ako dlho trvá jazda z dolnej stanice do hornej (v minútach)?
26
33 J / 33 S
Nech ABCD je kosoštvorec a body M, N, rôzne od bodov A, B, C, ležia postupne na úsečkách AB, BC tak, že DMN je rovnostranný trojuholník a AD = MD. Určte veľkosť uhla ABC (v stupňoch).
100^\circ
34 J / 34 S
Koľkými spôsobmi môžeme zafarbiť políčka tabuľky 2 \times 7 zelenou a žltou farbou tak, aby sa v tabuľke nenachádzalo ani zelené, ani žlté L-ko?
Poznámka: L-ko je ľubovoľne natočený nasledujúci útvar:

130
35 J / 35 S
Mišo je vášnivý zberateľ diamantov, ale vlastní zatiaľ menej ako 200 diamantov. Rozdelil všetky svoje diamanty na niekoľko (aspoň na dve) kôpok tak, aby
- každé dve kôpky obsahovali rôzny počet diamantov,
- žiadna z kôpok neobsahovala práve dva diamanty,
- pre každú z kôpok platilo: ak ju rozdelíme na dve menšie kôpky, tak aspoň jedna z nových kôpok bude obsahovať rovnako veľa diamantov ako niektorá z pôvodných kôpok.
Aký najväčší počet diamantov môže Mišo vlastniť?
Poznámka: Kôpka pozostáva s nenulového počtu diamantov.
196
36 J / 36 S
Pripomeňme si, že v hre Kameň, papier, nožnice máme tri symboly: K – kameň, P – papier a N – nožnice, pre ktoré platí N>P, P>K, K>N a K=K, P=P, N=N, kde A>B znamená „A poráža B“ a A=B znamená „A hralo proti B, hra skončila remízou“. Turnaj v hre Dvojruký Kameň, papier, nožnice bez opakovania medzi hráčmi P_1 a P_2 pozostáva z 9 hier. V každej hre si každý hráč vyberie dvojicu (\ell_i,r_i), kde \ell_i, resp. r_i je symbol, ktorý hráč P_i ukáže na pravej, resp. ľavej ruke. Počas celého turnaja si musí každý hráč vybrať každú dvojicu symbolov práve raz. Následne sa zvlášť vyhodnotia symboly hráčov na ľavých rukách a symboly na pravých rukách (podľa pravidiel hry Kameň, papier, nožnice). Hráč dostane za každú výhru 2 body, za každú remízu 1 bod a za každú prehru 0 bodov. V jednej hre sa teda celkom rozdelia 4 body. Predpokladajte, že obaja hráči volia dvojice symbolov náhodne. Aká je pravdepodobnosť, že každá z deviatich hier v turnaji skončí remízou (t. j. so skóre 2:2)?
3!^3/9!=1/1680
37 J / 37 S
Plášť telesa je zložený z ôsmych rovnostranných trojuholníkov a šiestich štvorcov, ako je vyznačené na obrázku:
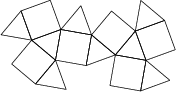
Predpokladajte, že dĺžka každej z hrán telesa je 1\,\text{km}, aký je objem celého telesa (v \text{km}^3)?
\frac 53 \sqrt 2
38 J / 38 S
Nájdite jediného trojciferného prvočíselného deliteľa čísla 999\,999\,995\,904.
601
39 J / 39 S
Trinásť včiel: jedna malá včela a dvanásť veľkých včiel žije v 37-bunkovom včeľom pláste. Veľká včela využíva na svoj život 3 susedné bunky včelieho plástu a malá včela žije v jednej bunke včelieho plástu (tak ako je vyznačené na obrázku). Koľkými spôsobmi môžeme 37-bunkový plást rozdeliť tak, aby každá zo včiel mala svoje bývanie podľa zadaných podmienok?
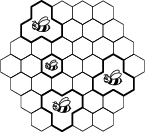
20
40 J / 40 S
Rovnostranný trojuholník ABC je vpísaný do kružnice \omega. Bod X leží na kratšom oblúku BC kružnice \omega a T je priesečník AB a CX. Ak |AX| = 5 a |TX|= 3, určte |BX|.
15/8
41 J / 41 S
Nech ABC je rovnostranný trojuholník. Vnútorný bod P trojuholníka ABC sa nazýva žiariaci, ak existuje práve 27 polpriamok, ktoré vychádzajú z bodu P a rozdeľujú trojuholník ABC na 27 menších trojuholníkov rovnakého obsahu. Určte počet žiariacich bodov v trojuholníku ABC.
\binom{26}{2} = 325
42 J / 42 S
Koľko kladných deliteľov čísla 2016^2 menších ako 2016 nie je deliteľom čísla 2016?
47
43 J / 43 S
Nech Vypočítajte Z_1 + Z_2 + \dots + Z_{2016}.
\frac12 (4033\sqrt{4033} - 1)
44 J / 44 S
Z celých čísel a_0, a_1, a_2 \dots vytvoríme postupnosť nasledovným spôsobom: Ak a_i je deliteľné tromi, tak a_{i+1}=a_i /3; v opačnom prípade a_{i+1}=a_i +1. Pre koľko rôznych kladných celých čísel a_0 dosiahne táto postupnosť hodnotu 1 prvýkrát práve v 11-tom kroku (t.j. a_{11} = 1, ale a_0, a_1, \dots, a_{10} \neq 1)?
423
45 J / 45 S
Nech ABCD, AEFG a EDHI sú obdĺžniky so stredmi postupne K, L a J. Predpokladajme, že body A, D, E sú postupne vnútornými bodmi úsečiek HI, FG, BC a |\angle AED| = 53^\circ. Určte v stupňoch veľkosť uhla JKL.
74^\circ
46 J / 46 S
Kubo zobral niekoľko (nie nutne rôznych) čísel z množiny \{-1, 0, 1, 2\} tak, že ich súčet bol 19 a súčet ich druhých mocnín bol 99. Akú najväčšiu hodnotu mohol nadobudnúť súčet tretích mocnín vybraných čísel?
133
47 J / 47 S
Nájdite najväčšie 9-ciferné číslo spĺňajúce nasledujúce vlastnosti:
- všetky jeho cifry sú rôzne;
- pre každé k=1,2,\ldots,9 platí, že keď vyškrtneme jeho k-tu cifru (zľava), dostaneme 8-ciferné číslo deliteľné číslom k.
876\,513\,240
48 J / 48 S
Bod P leží vnútri obdĺžnika ABCD so stranou |AB|=12. Každý z trojuholníkov ABP, BCP, DAP má svoj obvod číselne rovnaký ako svoju plochu. Aký je obvod trojuholníka CDP?
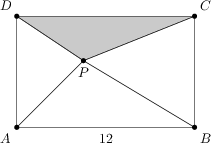
25
49 J / 49 S
Na tabuli je napísaná dvojica celých čísel (0,0). V každom kroku ju nahradíme nasledovným spôsobom: Ak je na tabuli dvojica (a,b), nahradíme ju dvojicou (a+b+c,b+c), kde buď c = 247, alebo c = -118. (číslo c si môžeme vybrať v každom kroku). Nájdite najmenší nenulový počet krokov, po ktorých sa na tabuli môže objaviť dvojica (0,b) pre nejaké celé číslo b.
145
50 J / 50 S
Jeden cikcak pozostáva z dvoch rovnobežných opačne orientovaných polpriamok, ktorých počiatočné body sú spojené úsečkou. Aký je najväčší počet oblastí, na ktoré môžeme rozdeliť rovinu desiatimi cikcakmi?
416
51 J / 51 S
Majme štvorsten v ktorom každá jeho stena je trojuholník s dĺžkami strán 1, \sqrt 2, a c a polomer gule opísanej tomuto štvorstenu je 5/6. Určte c.
\sqrt{23}/3
52 J / 52 S
Barman Milan pripravuje veľkú uvítaciu párty. Uložil do radu 2016 kokteilových pohárov, v každom z nich bol lahodný višňový kokteil. Pre dokončenie príprav je jeho úlohou prikryť jeden pohár strieborným viečkom, položiť sochu na vrch vrchnáka a rozdeliť nepárny počet višní do nezakrytých pohárov, do každého pohára najviac jednu višňu. Koľko rôznych rozmiestnení višní a viečka môže Milan dosiahnuť, ak má byť viac višní napravo od viečka ako naľavo?
2016\cdot 2^{2013}
53 J / 53 S
Máme danú drevenú kocku, ktorej povrch je natretý na zeleno. Ďalej máme 33 navzájom rôznych rovín, z ktorých sa každá rovina nachádza medzi nejakými dvoma protiľahlými stenami kocky a je s nimi rovnobežná. Týchto 33 rovín delí kocku na niekoľko menších kvádrov. Počet kvádrov, ktoré majú aspoň jednu stenu zelenú, je rovnaký ako počet kvádrov, ktoré nemajú žiadnu stenu zelenú. Určte celkový počet kvádrov, na ktoré je kocka rozdelená.
1260 alebo 1344
54 J / 54 S
Majme dané prirodzené číslo n, nech p(n) je súčin nenulových cifier čísla n. Nájdite najväčšieho prvočíselného deliteľa čísla p(1)+\dots+p(999).
103
55 J / 55 S
Nech \{a_n\}_{n=1}^\infty je rastúca postupnosť kladných celých čísel taká, že 9\mid a_{3k-2}, 14\mid a_{3k-1} a 19\mid a_{3k} pre všetky kladné celé čísla k. Nájdite najmenšiu možnú hodnotu a_{2016}.
14478
56 J / 56 S
Nech P je vnútorný bod trojuholníka ABC. Body D, E, F ležia postupne na úsečkách BC, CA, AB tak, že priamky AD, BE, CF sa pretínajú v bode P. Ak viete, že |PA|=6, |PB|=9, |PD|=6, |PE|=3 a |CF|=20, vypočítajte obsah trojuholníka ABC.
108
57 J / 57 S
Nájdite posledné dve cifry pred desatinnou čiarkou čísla (7 + \sqrt{44})^{2016}.
05






















