1 J
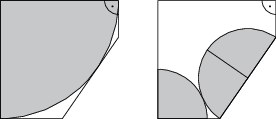
Die Fenster in einer alten Straßenbahn sehen aus wie hier abgebildet. Die abgerundeten Ecken werden von Viertelkreisen mit Radius 10\,\text{cm} gebildet. Ein Teil des Schiebefensters wurde 10\,\text{cm} weit geöffnet, wie im zweiten Bild zu sehen ist. Die Höhe des geöffneten Bereichs ist 13\,\text{cm}. Wie groß ist die Fläche der Öffnung in \text{cm}^2?
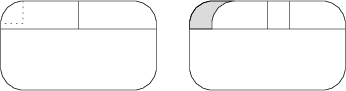
130
2 J
Ein Rechteck ist wie abgebildet in neun kleinere Rechtecke unterteilt. Die Zahl, die in einem kleinen Rechteck steht, gibt den Umfang dieses kleinen Rechtecks an. Welchen Umfang hat dann das große Rechteck?
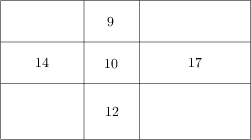
42
3 J
Marius radierte aus Versehen eine Ziffer einer vierstelligen Primzahl weg und erhielt 630. Wie lautet diese Primzahl?
6301
4 J
Die Star-Architektin Pauline will sich in ihrem rechteckigen Grundstück mit den Seitenlängen 35\, {\rm m} und 25\, {\rm m} ein ganz modernes fünfeckiges Haus bauen. Die Grundfläche des Hauses passt sie in das Grundstück ein wie in der Abbildung zu sehen ist. Dabei markieren die Punkte am Rand jeweils einen Abstand von 5\,\text{m}. Welchen Anteil an der Gesamtfläche nimmt die Grundfläche des Hauses ein?
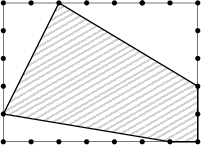
\frac{41}{70}
5 J
Das abgebildete quadratische Gitter von 16 Punkten enthält die Ecken von neun 1\times 1-Quadraten, vier 2\times 2-Quadraten und einem 3\times 3-Quadrat, also von insgesamt 14 Quadraten, deren Seiten parallel zu den Seiten des Gitters sind. Was ist die kleinste Anzahl an Gitterpunkten, die weggenommen werden können, so dass nach deren Entfernung bei jedem der 14 Quadrate mindestens ein Eckpunkt fehlt?

4
6 J
Bestimme die Einerziffer der Summe der Quadratzahlen 1^2+2^2+3^2+\cdots +2017^2.
5
7 J
Schreibe den Quotienten als einen vollständig gekürzten Bruch \dfrac{a}{b} mit positiven ganzen Zahlen a und b.
Hinweis: Der Querstrich bedeutet hier periodische Wiederholung in der Dezimalbruchentwicklung, beispielsweise ist 0.\overline{123} = 0.123123123\ldots
\frac{11}{12}
8 J
Passau hat einen triangelförmigen Bahnhof. Anna, Benjamin und Christoph beobachten den Zugverkehr in Linz, Regensburg und Waldkirchen an den von Passau kommenden Gleisen und zählen dort sowohl die einfahrenden als auch die abfahrenden Züge: Anna zählt 190, Benjamin 208 und Christoph 72. Wie viele Züge gingen von Linz nach Regensburg oder umgekehrt, wenn kein Zug in Passau startet, endet oder dort seine Richtung ändert?

163
9 J
Bestimme alle natürlichen Zahlen x < 10\,000 mit der Eigenschaft, dass x eine Viererpotenz einer geraden Zahl ist und durch Vertauschen der Ziffern von x eine Viererpotenz einer ungeraden Zahl entsteht. Hinweis: Dabei darf das Ergebnis einer Vertauschung nicht mit einer Null beginnen.
256
10 J
Im Parallelogramm ABCD schneidet eine Gerade durch den Punkt C die Seite AB im Punkt E so, dass \overline{EB} =\frac 15\, \overline{AE} erfüllt ist. Die Strecke CE schneidet die Diagonale BD im Punkt F. Bestimme das Verhältnis \overline{BF} : \overline{BD}.
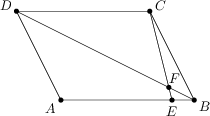
1 : 7
11 J / 11 S
Ein großes Haus hat 100 nummerierte Wohneinheiten. In jeder Wohnung ist entweder eine Person oder sind zwei oder drei Personen zu Hause. Die Gesamtzahl der Einwohner in den Wohnungen Nr. 1 bis Nr. 52 ist 56 und die Gesamtzahl der Leute in den Wohnungen von Nr. 51 bis Nr. 100 ist 150. Wie viele Leute leben in diesem Haus?
200
12 J / 12 S
Als ersten Schritt eines Spieles schrieb Tobias die Zahl 3 mit einem roten und die Zahl 2 mit einem grünen Stift auf ein Blatt Papier. In den folgenden Schritten schrieb er die Summe der beiden Zahlen aus dem vorherigen Schritt in Rot auf und ihre (positive) Differenz in Grün. Welche Zahl schrieb er im 2017-ten Schritt in roter Farbe auf?
3\cdot2^{1008}
13 J / 13 S
Rotkäppchen befindet sich am Eingang des Rechtwinkligen Waldes. Es muss möglichst schnell von A nach B kommen. Dazu kann es am Waldrand entlang einen Weg der Länge 140\,\text{m} gehen. Natürlich kennt es die Dreiecksungleichung und weiß, dass der direkte Weg kürzer wäre. Leider gibt es aber von A nach B nur einen Zickzackweg mit zwei rechtwinkligen Abbiegungen durch den Wald, wie in der Skizze zu sehen ist. Wenn Rotkäppchen wüsste, dass dieser Weg kürzer als 140\,\text{m} ist, würde es diesen Weg nehmen. Berechne die Länge des Zickzackweges durch den Wald in Metern!
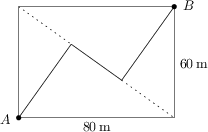
124
14 J / 14 S
Achtstellige Palindrome sind Zahlen der Form \overline{abcddcba}, wobei a, b, c und d nicht notwendigerweise verschiedene Ziffern sind und a\not= 0 gilt. Wie viele achtstellige Palindrome haben die Eigenschaft, dass man nach dem Streichen einiger Ziffern die Zahl 2017 als Ergebnis bekommt?
8
15 J / 15 S
Für eine positive ganze Zahl n sei \operatorname{S} (n) die Summe ihrer Ziffern und \operatorname{P}(n) das Produkt ihrer Ziffern.
Wie viele positive ganze Zahlen gibt es, für die n = \operatorname S (n) + \operatorname P (n) gilt?
9
16 J / 16 S
Ein Fabrikbesitzer beschäftigt 100 Angestellte. Jeder Gruppenleiter verdient 5 000 € im Monat, jeder Arbeiter 1 000 € und jeder Teilzeitbeschäftigte nur 50 €. Der Fabrikbesitzer hat von jeder dieser drei Arten mindestens einen Angestellten und zahlt jeden Monat 100 000 € Lohn aus. Wie viele Gruppenleiter sind in der Fabrik beschäftigt?
19
17 J / 17 S
Das abgebildete Mosaik ist ausschließlich aus regelmäßigen Vielecken zusammengesetzt. Das Sechseck und das dunkelgraue Dreieck besitzen denselben Umkreis. Bestimme den Flächeninhalt des dunkelgrauen Dreiecks, wenn der Flächeninhalt eines schraffierten Dreiecks 17 beträgt.
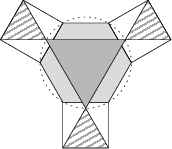
51
18 J / 18 S
Im Zuge der Renovierung des Bahnhofs in Passau werden auch speziell gepflasterte Wege für sehbehinderte Personen angelegt. Die Form dieser Pflasterung ist in der Abbildung zu sehen. Leider sind nur noch Platten der Größe 1\times 2 übrig geblieben. Wie viele Möglichkeiten gibt es, mit solchen Platten den Weg auszulegen? Hinweis: Die Platten unterscheiden sich nicht und zwei Pflasterungen sind verschieden, wenn Platten an einer Stelle anders angeordnet sind.
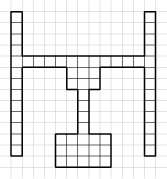
15
19 J / 19 S
Patricia suchte sich eine natürliche Zahl n aus. Dann nahm sie einen (positiven) Teiler von n, multiplizierte ihn mit 4, subtrahierte den Wert dieses Produktes von n und erhielt 2017 als Ergebnis. Bestimme alle Zahlen, die Patricia sich ausgesucht haben könnte.
2021, 10085
20 J / 20 S
Marianne und Hilde sind so gute Freundinnen, dass sie immer miteinander zu reden beginnen, sobald sie nebeneinander sitzen. Fünf Schülerinnen, unter ihnen auch Marianne und Hilde, wollen ein ernstes Thema konstruktiv diskutieren. Deshalb wollen sie auf fünf Stühlen so um einen runden Tisch sitzen, dass Marianne und Hilde nicht direkt nebeneinander sitzen. Wie viele verschiedene Möglichkeiten gibt es dafür, wenn Anordnungen, die durch Drehungen auseinander hervorgehen, als unterschiedlich gezählt werden?
60
21 J / 21 S
In der Abbildung ist AB der Durchmesser eines Kreises mit Mittelpunkt M. Die Punkte D und C liegen so auf dem Kreis, dass AC\perp DM erfüllt ist und \angle MAC = 56^\circ gilt. Bestimme die Größe des spitzen Winkels zwischen den Strecken AC und BD in Grad.
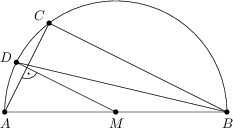
73
22 J / 22 S
Eine geometrische Figur wird nacheinander aus Einheitsquadraten aufgebaut, indem Kopien einer Stufe wie in der Abbildung zu einer neuen Stufe zusammengesetzt werden. Wie lang ist die dicke Begrenzungslinie der Figur in Stufe sechs?
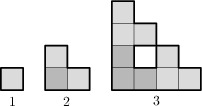
488
23 J / 23 S
In einer Zusammenkunft von Superhelden und Schurken waren alle 2017 Plätze um einen großen runden Tisch besetzt. Die Superhelden sagen immer die Wahrheit, wohingegen die Schurken immer lügen. Jede Person, die am Tisch saß, sagte aus, dass sie zwischen einem Superhelden und einem Schurken sitzt. Aus ungeklärten Gründen machte genau ein Superheld einen Fehler. Wie viele Superhelden waren anwesend?
1345
24 J / 24 S
Bestimme alle positiven reellen Zahlen x, die die Gleichung erfüllen.
\sqrt[2016]{2017}
25 J / 25 S
Leo möchte die Kanten eines regelmäßigen Dodekaeders in einer speziellen Art und Weise anmalen: Er wählt sich einen Filzstift, setzt ihn an einem Eckpunkt des Dodekaeders an und fährt damit entlang von zusammenhängenden Kanten ohne den Stift abzusetzen und ohne eine Kante zweimal anzumalen, bis er den Stift entweder freiwillig absetzt oder er dazu gezwungen wird. Dann nimmt er einen Filzstift mit einer anderen Farbe und beginnt erneut, noch nicht eingefärbte zusammenhängende Kanten anzumalen. Er macht auf diese beschriebene Art, jedes Mal mit einer neuen Farbe, so lange weiter, bis alle Kanten des Dodekaeders genau einmal eingefärbt sind. Was ist die kleinste Anzahl an Farben, die Leo benutzen kann?
Hinweis: Ein regelmäßiges Dodekaeder ist ein Körper mit zwölf kongruenten regelmäßigen Fünfecken als Flächen wie in der Abbildung zu sehen ist.
10
26 J / 26 S
Der Landschaftsarchitekt Severin ist beauftragt, einen dreieckigen Schotterweg rund um einen neuen Badesee anzulegen. Die Seitenlängen des Dreiecks \triangle ABC in der Mitte des Weges betragen a=80\, {\rm m}, b=100\, {\rm m} und c=120\, {\rm m}. Die Ränder des Weges sollen jeweils einen Abstand von 1\, {\rm m} zu diesem Dreieck haben, so wie es in der Abbildung dargestellt ist. Wie viele Kubikmeter feinen Schotter muss Severin bestellen, wenn der Belag des Schotters durchschnittlich 4\, {\rm cm} hoch sein soll?
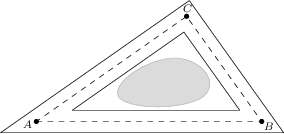
24
27 J / 27 S
Finde alle vierstelligen Quadrate ganzer Zahlen, wobei die ersten beiden Ziffern gleich sein sollen und die letzen beiden Ziffern auch.
7744
28 J / 28 S
Auf einem Volksfest gibt es eine Tombola mit folgenden Spielregeln: Man darf zuerst eine von vier nicht unterscheidbaren Boxen auswählen und dann eine Kugel aus der gewählten Box ziehen. Ist die gezogene Kugel weiß, so hat man gewonnen, ist sie schwarz, so hat man verloren. Ist beispielsweise die Verteilung der Kugeln in den vier Boxen wobei jedes Paar (w,s) eine Box mit w weißen und s schwarzen Kugeln repräsentiert, dann gewinnt man mit einer Wahrscheinlichkeit von \frac{5}{8}. Jeder tausendste Teilnehmer erhält einen Super-Joker: Er darf selber alle Bälle in den Boxen umverteilen, muss dabei aber in jede Box mindestens eine Kugel legen. Anschließend werden die Boxen gemischt, der Teilnehmer darf eine davon auswählen und daraus dann eine Kugel ziehen. Johanna hatte Glück und hat den Super-Joker gewonnen. Welche maximale Gewinnwahrscheinlichkeit kann sie durch geeignetes Umverteilen der Kugeln im obigen Beispiel erreichen?
\frac{51}{58}
29 J / 29 S
Ein Bus, ein Lastwagen und ein Motorrad fahren mit konstanten Geschwindigkeiten. Sie passieren in gleichen Zeitintervallen einen Kontrollposten in der genannten Reihenfolge. Bei einem etwas weiter entfernten zweiten Kontrollposten entlang der Straße kommen sie wieder in den gleichen Zeitabständen vorbei, diesmal allerdings in der geänderten Reihenfolge Bus, Motorrad, Lastwagen. Wie schnell fährt der Bus in \text{km/h}, wenn der Lastwagen mit einer Geschwindigkeit von 60\,\text{km/h} und das Motorrad mit 120\,\text{km/h} unterwegs sind?
80
30 J / 30 S
Bestimme alle Möglichkeiten dafür, in dem nachfolgenden Satz alle Lücken so mit natürlichen Zahlen zu füllen, dass eine wahre Aussage entsteht:
„In diesem Satz sind \boxed{\strut\quad}\% der vorkommenden Ziffern größer als 4, \boxed{\strut\quad}\% kleiner als 5 und \boxed{\strut\quad}\% entweder 4 oder 5.“
50,\, 50,\, 60
31 J / 31 S
Pauls Herde weidet auf einer dreieckigen Wiese mit den Eckpunkten A, B und C. Da sich seine gefleckten Kühe nicht mit den ungefleckten vertragen, hat Paul einen zwanzig Meter langen Zaun senkrecht zur Seite AC eingezogen, der beim Punkt P auf dieser Seite beginnt und im Punkt B endet. Dadurch wird die Wiese in zwei rechtwinklige Dreiecke aufgeteilt. Aber kurz danach wiesen die gefleckten Kühe, die in dem Teil weideten, der den Punkt A enthält, darauf hin, dass das Verhältnis \overline{AP} : \overline{PC} = 2 : 7 ist, und forderten eine gerechte Aufteilung. Also ersetzte Paul den Zaun durch einen neuen parallel zum alten, der die Wiese in zwei gleiche Teile aufteilte und ebenfalls an den Grenzen der Wiese endete. Wie lang war der neue Zaun in Metern?
30 \sqrt{\frac27}
32 J / 32 S
An der Tafel standen fünf nicht notwendigerweise verschiedene reelle Zahlen. Für jedes mögliche Paar von diesen Zahlen berechnete Julien dessen Summe, schrieb diese zehn Ergebnisse an die Tafel und wischte die ursprünglichen Zahlen weg. Bestimme alle möglichen Werte, die das Produkt der weggewischten Zahlen annehmen kann.
-144
33 J / 33 S
Schreibe die Zahl 333 als Summe von Quadraten verschiedener positiver ungerader Zahlen.
3^2 + 5^2 + 7^2 + 9^2 + 13^2
34 J / 34 S
Ellen wählte drei reelle Zahlen a, b, c und definierte damit die Operation \odot durch Als Übung berechnete sie 1 \odot 2 = 3 und 2 \odot 3 = 4. Ferner bemerkte sie, dass es eine reelle Zahl u ungleich Null gibt, so dass z \odot u = z für jede reelle Zahl z gilt. Welchen Wert hat u?
4
35 J / 35 S
Drei Kreise mit Radius r und ein Kreis mit Radius 1 berühren einander und eine Gerade wie in der Abbildung zu sehen ist. Bestimme r.
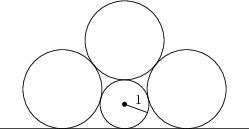
\frac{1+\sqrt{5}}{2}
36 J / 36 S
Auf eine alte Betonwand hatte jemand fünf nicht notwendigerweise verschiedene reelle Zahlen gesprüht, deren Summe 20 war. Eva berechnete für jedes Paar dieser Zahlen deren Summe und nahm von dieser Summe jeweils nur den ganzzahligen Anteil. Dann addierte sie alle diese ganzen Zahlen. Bestimme den kleinsten Wert, den diese Summe annehmen kann.
72
37 J / 37 S
Für eine zusammengesetzte positive ganze Zahl n sei \xi(n) die Summe der drei kleinsten positiven Teiler und \vartheta(n) die Summe der beiden größten Teiler von n. Bestimme alle zusammengesetzten Zahlen n, für die \vartheta(n)=(\xi(n))^4 erfüllt ist.
Hinweis: Mit einem Teiler ist hier ein positiver, nicht notwendigerweise echter Teiler gemeint.
864
38 J / 38 S
Eine Maus sitzt im linken unteren Feld eines 3\times 3-Gitters. Ihr Ziel ist es, ein Stück Käse zu erreichen, das im rechten oberen Feld liegt. Dabei darf sie nur Schritte von einem Feld zum nächsten machen, wenn diese Felder durch eine Kante miteinander verbunden sind. Wie viele Möglichkeiten gibt es, einige, vielleicht auch keines der freien Felder mit Hindernissen zu belegen, so dass die Maus immer noch ihr Ziel erreichen kann?
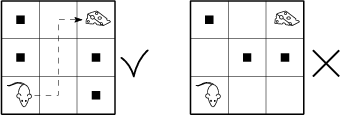
51
39 J / 39 S
Unter allen Paaren (x, y) reeller Zahlen, die die Gleichung erfüllen, sei (x_0, y_0) dasjenige mit minimalem x_0. Bestimme y_0.
-3
40 J / 40 S
Gegeben sei ein rechtwinkliges Dreieck \triangle ABC mit dem rechten Winkel bei C. Die Punkte D und E liegen so auf der Seite AB, dass D zwischen A und E liegt und die Strecken CD und CE den Winkel \angle ACB in drei gleiche Teile zerlegen. Bestimme das Verhältnis \overline{AC} : \overline{BC}, wenn \overline{DE} : \overline{BE} = 8:15 gilt.
\frac{4}{11}\sqrt3
41 J / 41 S
Michael spielt das folgende Spiel: Seine Aufgabe besteht darin, eine ganze Zahl zwischen 1 und N (beide inklusive) zu erraten. In jedem Zug wählt er eine Zahl aus diesem Intervall. Wenn die Zahl die gesuchte ist, endet das Spiel. Sollte die genannte Zahl nicht die gesuchte sein, so erfährt er, ob er zu hoch oder zu niedrig geraten hat. Hat er zu hoch geraten, muss er 1 € zahlen, hat er zu niedrig geraten, so muss er 2 € zahlen. Er muss nichts zahlen, wenn er die Zahl erraten hat. Wie lautet die größte ganze Zahl N, für welche Michael das Spiel immer beenden kann, ohne mehr als 10 € auszugeben?
232
42 J / 42 S
Gegeben sind die positiven ganzen Zahlen a, b und c. Es gilt a \geq b \geq c und Gib alle möglichen Werte für a an!
134
43 J / 43 S
Ein Alien-Raumschiff hat die Form einer perfekten Kugel vom Radius r mit drei parallelen vertikalen geraden Standfüßen der Länge 1\,\text{af} (Alien Fuß) mit vernachlässigbarer Breite. Die unteren Enden der Standfüße bilden ein gleichseitiges Dreieck mit der Seitenlänge 9\,\text{af}. Wenn das Raumschiff auf einer ebenen Fläche steht, berührt der niedrigste Punkt der Kugel die Fläche. Wie groß ist der Radius r in \text{af}?
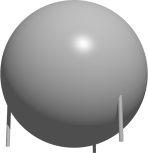
14
44 J / 44 S
Adam, Bert, Christoph und Daniel haben eine große Menge an Haselnüssen gesammelt. In der Nacht erwacht Adam mit einem unwiderstehlichen Appetit auf Haselnüsse. Durch Zählen findet er Folgendes heraus: Wenn man eine Haselnuss entfernt, so kann der Rest in vier Haufen mit gleich großer Anzahl an Nüssen aufgeteilt werden. Also entfernt er eine Nuss und isst seinen Anteil (ein Viertel des Restes). Später in der Nacht möchte auch Bert Haselnüsse essen. Er stellt fest, dass es wieder eine extra Nuss gibt. Auch er entfernt sie, teilt die restlichen Nüsse in vier Haufen mit gleicher Anzahl auf und vertilgt sogleich sein Viertel des Restes. Bis zum Morgen ergeht es Christoph und Daniel genauso. Als sich die vier Freunde am Morgen treffen, sehen sie, dass die übrig gebliebene Anzahl an Nüssen nach dem Entfernen einer weiteren Nuss immer noch durch vier teilbar ist. Was ist die kleinstmögliche Anzahl an Haselnüssen, die die Brüder gesammelt haben können?
1021
45 J / 45 S
Eine positive ganze Zahl soll praktisch heißen, wenn alle ihre Primteiler aus der Menge \{2,3,7\} sind. Wie viele praktische Zahlen gibt es in der Menge \{1000, 1001, \ldots, 2000\}?
19
46 J / 46 S
Kaiser Decimus verbietet in einem kaiserlichen Dekret ab sofort die Verwendung der Ziffer 0, die von seinem Vorgänger Nullus eingeführt wurde. Er erteilt außerdem die Anweisung, ab nun die Ziffer \mathrm D zu verwenden, die für die Zahl 10 steht. Er sieht sich als Erfinder des sogenannten Decimus Systems, in dem jede positive ganze Zahl immer noch eine eindeutige Darstellung besitzt. Beispielsweise ist Um seinem Volk den Übergang ins neue System zu erleichtern, lässt Kaiser Decimus eine Liste mit allen ganzen Zahlen von 1 bis einschließlich \mathrm{DDD} anfertigen. Wie oft kommt die neue Ziffer \mathrm D in dieser Liste vor?
Hinweis: Kommt die Ziffer \mathrm D in einer bestimmten Zahl mehrmals vor, so wird jedes vorkommende \mathrm D einzeln gezählt, zum Beispiel wird sie in der Zahl \mathrm{DD} zwei Mal gezählt.
321
47 J / 47 S
Der Inkreis \omega eines Quadrates ABCD berührt das Quadrat in den Punkten W, X, Y und Z, die in dieser Reihenfolge auf den Seiten AB, BC, CD und DA liegen. Sei E ein Punkt auf dem kürzeren Kreisbogen von \omega zwischen W und X und sei F der Schnittpunkt der Geraden BC mit der Geraden EY. Bestimme den Flächeninhalt des Dreiecks \triangle FCY, wenn \overline{EF} = 5 und \overline{EY} = 7 ist.
21
48 J / 48 S
Von dem Kryptogramm sind folgende Eigenschaften bekannt: Verschiedene Buchstaben stehen für verschiedene Ziffern und keine der Zahlen beginnt mit der Ziffer Null. Bezeichnet man mit \operatorname{Q}(n) die Quersumme einer natürlichen Zahl n, so gilt \operatorname{Q}(W\!E)= 11, \operatorname{Q}(LIKE)=23 und \operatorname{Q}(N\!ABOJ)=19. Bestimme als Lösung die fünfstellige Zahl, die sich hinter N\!ABOJ verbirgt.
60\,724
49 J / 49 S
Bestimme alle positiven ganzen Zahlen n mit der Eigenschaft, dass die Summe aller echten Teiler genau 63 beträgt. Hinweis: Ein echter Teiler d von n erfüllt 1 < d < n.
56, 76, 122
50 J / 50 S
Georg fährt ein cooles Auto mit quadratischen Hinterrädern und kreisförmigen Vorderrädern. Ein derartiges Fahrzeug ist für gewöhnlich eher unbequem zu fahren, aber Georg hat für die Hinterräder einen äußerst wirkungsfähigen Stoßdämpfer eingebaut. Fährt Georg nämlich auf einer ebenen Straße, so hat die Unterkante des Autos immer den gleichen vertikalen Abstand vom Boden. Die Seitenlänge der Hinterräder beträgt 40\,\text{cm} und ihre Achse ist in horizontaler Richtung fixiert. Wie groß ist der Radius der Vorderräder in cm, wenn die Hinterachse bei konstanter Vorwärtsbewegung des Autos exakt die Hälfte der Zeit einen kleineren und exakt die Hälfte der Zeit einen größeren Abstand vom Straßenboden hat als die Vorderachse?
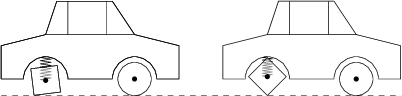
10 \sqrt{7}
51 J / 51 S
Die Stadt der Zukunft hat die Form eines regulären 2017-Ecks. In jeder der Ecken befindet sich eine Metro-Station. Diese Stationen sind von 1 bis 2017 gegen den Uhrzeigersinn durchnummeriert und es gibt die zwei Metro-Linien Seiten-Linie S und Diagonalen-Linie D. Linie S fährt von Station a zu Station b, und nur in diese Richtung, genau dann, wenn a-b+1 durch 2017 teilbar ist. Von einer Station zur nächsten benötigt Linie S jeweils 1 Minute. Linie D fährt von Station a zu Station b genau dann, wenn 2b-2a+1 durch 2017 teilbar ist. Von einer Station zur nächsten benötigt Linie D jeweils 15 Minuten. Ferdinand ist ein passionierter Metro-Fahrer. Er möchte von der Station 1 abfahren und sucht eine Station n, sodass der zeitlich kürzeste Weg von Station 1 nach Station n unter allen zeitlich kürzesten Wegen von Station 1 zu einer anderen Station am längsten ist. Finde alle möglichen Werte für n.
1984, 1985
52 J / 52 S
Sei f(n) die Anzahl der positiven ganzen Zahlen, die genau n Stellen haben und deren Quersumme 5 beträgt. Bestimme, wie viele der 2017 ganzen Zahlen f(1), f(2), \dots, f(2017) die Einerziffer 1 haben.
202
53 J / 53 S
Die Skizze zeigt zwei zueinander ähnliche sechseckige Figuren mit den Seiten a, b, c und d bzw. A, B, C und D. Setzt man die beiden Figuren wie in der Abbildung zusammen, so entsteht eine große sechseckige Figur, die ebenfalls zu den beiden kleineren ähnlich ist. Bestimme das Verhältnis A : a.
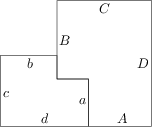
\sqrt{\frac{1+\sqrt 5}{2}}
54 J / 54 S
Bestimme alle Paare (a,b) positiver ganzer Zahlen, sodass alle Lösungen der beiden Gleichungen auch positive ganze Zahlen sind.
(2,2), (6,6), (7,8), (8,7)
55 J / 55 S
Das Dreieck \triangle ABC mit den Seitenlängen \overline{AB} = 3, \overline{BC} = 7 und \overline{AC} = 5 ist dem Kreis \omega einbeschrieben. Die Winkelhalbierende des Winkels \angle BAC schneidet die Seite BC im Punkt D und den Kreis \omega in einem anderen Punkt E. Es sei \gamma der Kreis mit dem Durchmesser DE. Die Kreise \omega und \gamma schneiden sich im Punkt E und einem zweiten Punkt F. Bestimme die Länge der Strecke AF.
\frac{30}{\sqrt{19}}
56 J / 56 S
Bestimme die Anzahl an geordneten Tripeln (x, y, z) aus nicht-negativen ganzen Zahlen x, y und z, die kleiner als 2017 sind, sodass der Ausdruck durch 2017 teilbar ist.
2017^2 + 1 = 4\,068\,290
57 J / 57 S
Andi und Manuel spielen ein Spiel mit einem fairen Spielwürfel, der zwei rote, zwei grüne und zwei blaue Seitenflächen hat. Die beiden würfeln abwechselnd und Andi darf beginnen. Sie würfeln so lange, bis einer der beiden alle drei Farben mindestens einmal gewürfelt hat – wer das zuerst schafft, gewinnt das Spiel. Mit welcher Wahrscheinlichkeit gewinnt Andi das Spiel?
81/140
58 J / 58 S
Bestimme die größte ganze Zahl n, für die die Gleichung mindestens ein Lösungspaar (k, n) ganzer Zahlen besitzt.
104
59 J / 59 S
Die Viertel-Pizzeria liefert ihre Viertelpizzas in speziellen fünfeckigen Pizzakartons, die sowohl für eine große Viertelpizza als auch für drei kleine Viertelpizzas Platz bieten wie in der Abbildung zu sehen ist. Wie groß ist der Radius einer kleinen Pizza in cm, wenn der Radius einer großen Pizza 30\,\text{cm} beträgt?
5(1+\sqrt{7}-\sqrt{2\sqrt{7}-4})























