1 J
Okna ve starší tramvaji vypadají jako na obrázku. Všechny zaoblené rohy jsou tvořeny oblouky kružnice o poloměru 10\,\text{cm}. Posuvné okénko je pootevřené na 10\,\text{cm}, jak je znázorněno na druhém obrázku. Výška posuvného okénka je 13\,\text{cm}. Jaký obsah v \text{cm}^2 má vzniklý otvor?
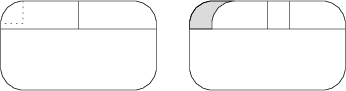
130
2 J
Obdélník je rozdělen na devět obdélníčků, jak znázorňuje obrázek. Do některých obdélníčků je vepsán jejich obvod. Určete obvod velkého obdélníku.
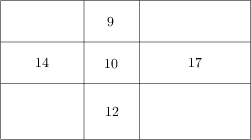
42
3 J
Kuba odstranil ze čtyřciferného prvočísla jednu cifru a dostal tak 630. Které prvočíslo to bylo?
6301
4 J
Uhlobaron Ptáček si nechal postavit velmi moderní pětiúhelníkový dům na obdélníkovém pozemku o stranách 35\, \mbox{m} a 25\, \mbox{m}. Půdorys domu je do pozemku zasazen jako na obrázku (sousední body na hranici jsou od sebe vzdáleny 5\,\mbox{m}.) Jakou poměrnou část obsahu celého pozemku tvoří zastavěná plocha?
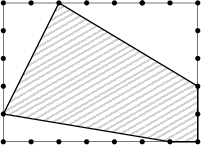
\frac{41}{70}
5 J
Čtvercová mřížka tvořená 16 body, kterou vidíme na obrázku, obsahuje vrcholy devíti čtverců 1\times 1, čtyř čtverců 2\times 2 a jednoho čtverce 3\times 3, celkem tedy 14 čtverců, jejichž strany jsou rovnoběžné se stranami mřížky. Jaký nejmenší počet bodů lze z mřížky odebrat, aby po jejich odstranění každému ze 14 čtverců scházel nejméně jeden vrchol?

4
6 J
Určete poslední číslici součtu
5
7 J
Vyjádřete podíl jako zlomek \dfrac{a}{b} v základním tvaru s přirozenými čísly a a b.
Poznámka: Horní pruh značí periodický desetinný rozvoj, kupříkladu 0{,}\overline{123} = 0{,}123123\ldots
\frac{11}{12}
8 J
Přerovský železniční uzel má tvar trojúhelníku. Olin, Martina a Marian provádějí špionáž a sledují všechny vlaky, které projíždějí Přerovem. Svá pozorovací stanoviště mají pečlivě ukryta v blízkosti trati postupně ve směru na Hulín, na Olomouc a na Lipník. Během jednoho dne Olin napočítal 190, Martina 208 a Marian 72 vlaků. Kolik vlaků jelo ten den mezi Olomoucí a Hulínem, pokud víme, že žádný vlak nevyjíždí z Přerova, nekončí v něm, ani se v něm nemůže otočit a vrátit se zpět?
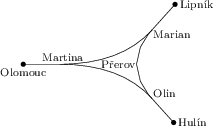
163
9 J
Najděte všechna přirozená čísla x < 10\,000 taková, že x je čtvrtou mocninou nějakého sudého čísla a zároveň můžeme zpřeházením cifer x dostat čtvrtou mocninu některého lichého čísla. Cifry přitom nesmíme přehazovat tak, aby výsledné číslo začínalo nulou.
256
10 J
Je dán rovnoběžník ABCD. Nechť E je bod na straně AB splňující |EB| =\frac 15\, |AE| a nechť úsečka CE protíná úhlopříčku BD v bodě F. Určete poměr |BF| : |BD|.
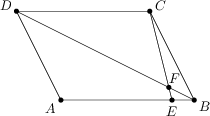
1 : 7
11 J / 11 S
Ve velké stáji je sto boxů, které jsou označené čísly 1 až 100. V jednom boxu mohou být jeden, dva, nebo tři koně. Je známo, že v boxech 1 až 52 je dohromady 56 koní a v boxech 51 až 100 je jich celkem 150. Kolik koní je dohromady ve stáji?
200
12 J / 12 S
Lucien napsal na tabuli červenou barvou číslo 3 a zelenou číslo 2. Pak vždy, když se mu aktuální čísla omrzela, obě smazal a místo nich napsal červeně jejich součet a zeleně absolutní hodnotu jejich rozdílu. Jaké bylo 2017. červené číslo, které se objevilo na tabuli?
3 \cdot 2^{1008}
13 J / 13 S
Červená Karkulka stojí v rohu A obdélníkového arboreta. Po svých předchozích zkušenostech v něm nechce trávit více času, než je nezbytně nutné, a ráda by se co nejrychleji dostala do protějšího rohu B. Má dvě možnosti: buď jít podél hranice a urazit 140 metrů, nebo jít klikatou cestičkou s dvěma pravoúhlými zatáčkami, jak je nakresleno na obrázku. Pomozte Karkulce rozhodnout se, kudy jít, a vyjádřete délku klikaté cestičky v metrech.
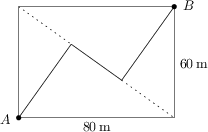
124
14 J / 14 S
Osmiciferný palindrom je číslo tvaru \overline{abcddcba}, přičemž cifry a, b, c a d nemusejí být nutně různé. Kolik osmiciferných palindromů má tu vlastnost, že z nich lze vynecháním několika cifer získat číslo 2017?
8
15 J / 15 S
Pro přirozené číslo n označme \operatorname S(n) součet jeho cifer a \operatorname P(n) jejich součin. Kolik existuje přirozených čísel n takových, že n=\operatorname S(n)+\operatorname P(n)?
9
16 J / 16 S
Na slovenském Ministerstvu švihlé chůze mají 100 zaměstnanců. Vedoucí oddělení bere měsíčně 5\,000 €, řadový pracovník 1\,000 € a brigádník 50 €. Celkově vydá ministerstvo na platech 100\,000 €. Určete, kolik vedoucích oddělení ministerstvo má, pokud víte, že zaměstnává alespoň jednoho vedoucího oddělení, alespoň jednoho řadového pracovníka a alespoň jednoho brigádníka.
19
17 J / 17 S
Mozaika na obrázku je tvořena pravidelnými mnohoúhelníky. Šestiúhelník a šedý trojúhelník jsou vepsány do stejné kružnice a obsah každého ze tří vyšrafovaných trojúhelníků je 17. Určete obsah šedého trojúhelníku.
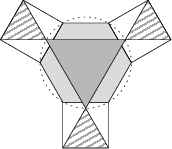
51
18 J / 18 S
Připravuje se rekonstrukce Masarykova nádraží, v rámci níž bude položena zcela nová dlažba. Před nástupišti by se měly nacházet barevné obrazce, které budou mít tvar jako na obrázku a budou vydlážděny dlaždicemi 1\times 2. Kolika způsoby lze jeden takový obrazec vydláždit? Dlaždice jsou všechny stejné a dvě vydláždění považujeme za různá, pokud je na jednom z nich spára v místě, kde na druhém je dlaždice.
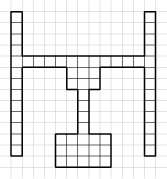
15
19 J / 19 S
Jirka si hrál s celým kladným číslem n. Na začátku si vybral nějakého jeho kladného dělitele, vynásobil ho čtyřmi a výsledek odečetl od n. Dostal tak číslo 2017. Najděte všechny možné hodnoty čísla n.
2021, 10085
20 J / 20 S
Anička s Davidem jsou dobří kamarádi a pokaždé, když sedí vedle sebe, si začnou povídat. Paní učitelka chce posadit pět dětí, mezi nimi i Aničku a Davida, na pět židlí rozmístěných kolem kulatého stolu, aby mohly společně pracovat na projektu. Nechce, aby Anička s Davidem seděli vedle sebe a vyrušovali. Kolika způsoby může děti rozesadit? Rozesazení, která se liší natočením, považujeme za různá.
60
21 J / 21 S
Na obrázku je AB průměrem kružnice se středem v M. Pro body C a D na kružnici platí, že AC\perp DM a |\sphericalangle MAC| = 56^\circ. Určete (ve stupních) velikost ostrého úhlu mezi přímkami AC a BD.
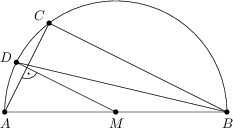
73^\circ
22 J / 22 S
Tvoříme posloupnost obrazců. Prvním obrazcem je čtvereček 1\times 1 a každý další vznikne slepením tří kopií předchozího obrazce (podél strany jednoho z jednotkových čtverečků), jak je znázorněno na obrázku. Jaká je délka zvýrazněné hranice šestého obrazce?
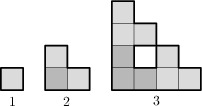
488
23 J / 23 S
Kolem velikého kulatého stolu s 2017 židlemi sedí andělé a démoni (každá židle je obsazena jedním z nich). Démoni vždy lžou a andělé vždy mluví pravdu. Každý u stolu řekl, že sedí mezi andělem a démonem. Z blíže nespecifikovaného důvodu se právě jeden anděl spletl. Kolik andělů sedí u stolu?
1345
24 J / 24 S
Najděte všechna kladná reálná čísla x splňující
\sqrt[2016]{2017}
25 J / 25 S
Vasil musí za trest obarvit hrany pravidelného dvanáctistěnu. Má to ale háček – žádnou hranu nesmí obarvit vícekrát a jednou barvou může malovat vždy jen jedním tahem po hranách, které spolu sousedí nějakým vrcholem. Když se pak dostane do nějakého vrcholu, z nějž vedou jen obarvené hrany, nebo když se prostě rozhodne skončit, musí si vzít fix nějaké barvy, kterou ještě nepoužil, a začít nový tah. Kolik nejméně barev potřebuje k obarvení všech hran?
Poznámka: Pravidelný dvanáctistěn je pravidelné trojrozměrné těleso s dvanácti pětiúhelníkovými stěnami jako na obrázku:
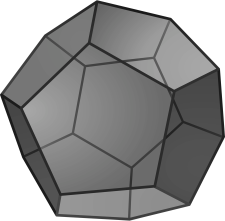
10
26 J / 26 S
Zahradní architekt Pepa má v plánu si okolo jezírka postavit trojúhelníkový chodníček. Jeho střed bude určen trojúhelníkem ABC o stranách délek a = 80\,\text{m}, b = 100\,\text{m} a c = 120 \,\text{m}. Okraje chodníčku mají být se stranami trojúhelníka rovnoběžné a vzdálené od nich 1\,\text{m}. Kolik \text{m}^3 štěrku bude Pepa potřebovat, pokud chce chodníček pokrýt 4\,\text{cm} vysokou vrstvou štěrku?
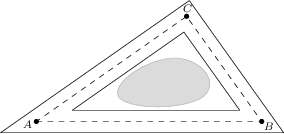
24
27 J / 27 S
Najděte všechny čtyřciferné čtverce tvaru \overline{xxyy}, kde x a y jsou ne nutně různé číslice.
Poznámka: Čtvercem zde rozumíme druhou mocninu kladného celého čísla.
7744
28 J / 28 S
Na Matějské pouti probíhá loterie. Ve čtyřech identických bednách se nachází celkem 18 bílých a 14 černých míčků. Soutěžící si vybere jednu z těchto čtyř beden a z ní vytáhne jeden míček. Pokud je vytažený míček bílý, soutěžící vyhrál, a pokud je černý, prohrál.
Je-li například rozložení míčků (6,6),\,(5,3),\,(4,0),\, (3,5), kde dvojice (b,c) označuje postupně počet bílých a černých míčků v bedně, potom je šance na výhru \frac{5}{8}.
Každý 1000. účastník loterie hraje superhru. Na začátku může míčky sám rozdělit do čtyř beden tak, aby byl v každé z nich alespoň jeden. Bedny jsou poté zamíchány, takže není možné určit, která je která, a účastník si vytáhne míček stejným způsobem jako výše. Jaká je největší možná šance na výhru v superhře?
\frac{51}{58}
29 J / 29 S
Motorová vozidla se na závodech pohybují konstantní rychlostí. Okolo stojícího diváka projel autobus, po t hodinách kamion a po dalších t hodinách motocykl. O něco dále na trati projela kolem jiného fanouška tato tři vozidla ve stejných intervalech, ale v jiném pořadí, a to autobus, motocykl, kamion. Jaká je rychlost autobusu v km/h, jestliže kamion jede rychlostí 60\,\text{km/h} a motocykl rychlostí 120\,\text{km/h}?
80
30 J / 30 S
Najděte všechny způsoby, jak se dají do obdélníčků v níže uvedeném výroku vepsat přirozená čísla tak, aby byl pravdivý: „V tomto výroku je \boxed{\phantom{00}}\,\% číslic větších než 4, \boxed{\phantom{00}}\,\% číslic menších než 5 a \boxed{\phantom{00}}\,\% číslic rovných 4 nebo 5.“
50, 50, 60
31 J / 31 S
Vaškův dobytek se pase na trojúhelníkové louce ABC. Protože jeho strakaté krávy se nesnesou s těmi jednobarevnými, postavil Vašek dvacet metrů dlouhý plot kolmý na stranu AC, který začíná v bodě P na této straně a končí v bodě B, jímž louku rozdělil na dva menší pravoúhlé trojúhelníky. To však záhy vyvolalo protesty strakatých krav (pasoucích se v části s bodem A), které poukázaly na to, že |AP| : |PC| = 2 : 7, a požadovaly spravedlivější dělení. Vašek tedy nahradil plot novým, jenž je rovnoběžný s tím starým a má oba konce na hranici louky, avšak dělí tuto louku na dvě části o stejném obsahu. Jaká je délka nového plotu v metrech?
30 \sqrt{\frac27}
32 J / 32 S
Na tabuli bylo napsáno pět reálných čísel (ne nutně různých). Honza postupně prošel všechny dvojice čísel a pro každou spočítal její součet. Pak napsal na tabuli všech deset výsledků a původní čísla smazal. Určete všechny možné hodnoty součinu smazaných čísel.
-144
33 J / 33 S
Zapište 333 jako součet druhých mocnin několika různých lichých přirozených čísel.
3^2 + 5^2 + 7^2 + 9^2 + 13^2
34 J / 34 S
ET popadl tři reálná čísla a, b, c a definoval operaci \odot jako x \odot y = ax + by + cxy. Aby zahnal nudu, spočítal si, že 1 \odot 2 = 3 a 2 \odot 3 = 4. Po dalším pachtění zjistil, že existuje nenulové reálné číslo u splňující z \odot u = z pro každé reálné z. Jaká je hodnota u?
4
35 J / 35 S
Tři kružnice o poloměru r, jedna kružnice o poloměru 1 a jedna přímka se vzájemně dotýkají způsobem naznačeným na obrázku. Určete hodnotu r.
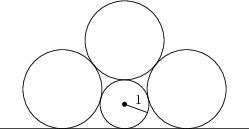
\frac{1+\sqrt{5}}{2}
36 J / 36 S
Na zeď matfyzáckých kolejí někdo nasprejoval pět (ne nutně různých) reálných čísel, jejichž součet byl 20. Karel postupně sečetl každou dvojici čísel a výsledek vždy zaokrouhlil dolů (tj. vzal největší celé číslo nepřesahující výsledek), čímž dostal deset celých čísel. Nakonec sečetl všechna tato nová čísla. Jakou nejmenší hodnotu součtu tak Karel mohl dostat?
72
37 J / 37 S
Pro složené kladné celé číslo n označme \xi(n) součet jeho tří nejmenších dělitelů a \vartheta(n) součet jeho dvou největších dělitelů. Najděte všechna složená čísla n, pro něž platí \vartheta(n)=(\xi(n))^4.
Poznámka: Za dělitele n považujeme všechna kladná celá čísla k, pro která je n/k opět celé číslo.
864
38 J / 38 S
Mlsná myška se nachází v levém dolním rohu šachovnice 3 \times 3 a touží po kousku sýra, který se povaluje v pravém horním rohu. Myška umí přecházet jen mezi políčky sousedícími hranou. Kolika způsoby můžeme na některá z volných políček (třeba i na žádné z nich) umístit překážky tak, aby se myška stále uměla dostat k sýru?
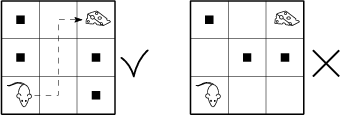
51
39 J / 39 S
Ze všech dvojic (x, y) reálných čísel splňujících označme (x_0, y_0) tu s nejmenším x_0. Najděte y_0.
-3
40 J / 40 S
Nechť ABC je pravoúhlý trojúhelník s pravým úhlem u vrcholu C. Dále D a E jsou body na straně AB, přičemž D leží mezi A a E a přímky CD a CE dělí úhel ACB na třetiny. Pokud |DE|:|BE| = 8:15, najděte |AC| : |BC|.
\frac{4\sqrt3}{11}
41 J / 41 S
Háňa propadla nové hazardní hře, v níž je cílem uhodnout neznámé přirozené číslo z intervalu 1 až N včetně. V každém tahu řekne Háňa některé číslo z tohoto intervalu. Pokud se trefí, hra končí, a v opačném případě jí krupiér prozradí, zda je její tip příliš velký, nebo příliš malý. Pokud je její číslo vyšší než hledané číslo, musí Háňa zaplatit 1 Kč, a pokud je nižší, zaplatí dokonce 2 Kč. Za správný tip se nic neplatí. Pro jaké největší N dokáže Háňa hru určitě dokončit, smí-li utratit nanejvýš 10 Kč?
232
42 J / 42 S
Pro kladná celá čísla a, b, c platí a \geq b \geq c a Zjistěte všechny vyhovující hodnoty a.
134
43 J / 43 S
Mimozemská kosmická loď má tvar dokonalé koule o poloměru R podepřené třemi rovnoběžnými svislými nohami o délce 1\,\text{ms} (mimozemský sáh) a zanedbatelné tloušťce. Dolní konce noh tvoří rovnostranný trojúhelník o straně délky 9\,\text{ms}. Když loď stojí na rovném povrchu, dotýká se ho také nejnižší bod koule. Jaký je poloměr R (v \text{ms})?
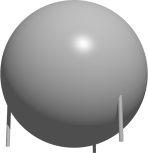
14
44 J / 44 S
Čtyři bratři, Albrecht, Bořivoj, Chrudoš a Dalimil, nasbírali v lese spoustu lískových oříšků. V noci Albrechta honila mlsná, takže se jich rozhodl pár sníst. Po přepočítání oříšků zjistil, že kdyby jich měli o jeden méně, šlo by je rozdělit na čtyři stejně velké hromádky. Proto jeden ořech zahodil, snědl svůj podíl (čtvrtinu zbytku) a šel spokojeně spát. O něco později hlad probudil i Bořivoje a i on zjistil, že jeden oříšek přebývá. I zahodil jej a schroustal čtvrtinu zbytku. Do rána se přesně totéž přihodilo i Chrudošovi a Dalimilovi. Když se za kuropění všichni bratři setkali, ukázalo se, že i nyní by po zahození jednoho ořechu bylo možné zbytek rozdělit na čtyři stejné hromádky. Jaké nejmenší množství ořechů mohli chlapci nasbírat?
1021
45 J / 45 S
Přirozené číslo nazýváme vychované, jestliže není dělitelné žádným prvočíslem různým od 2, 3 a 7. Kolik vychovaných čísel najdeme mezi čísly 1000, 1001, \dots, 2000?
19
46 J / 46 S
Císař Decimus zakázal číslici 0 (kterou zavedl jeho předchůdce Nullus). Nařídil místo ní používat číslici \mathrm D, představující hodnotu 10, čímž vznikla decimická soustava. I v ní má každé přirozené číslo jednoznačně daný zápis, například Aby změna číselné soustavy proběhla co možná nejsnáze, byl na velký obelisk vytesán seznam všech čísel od 1 do \mathrm{DDD} včetně. Kolikrát se v něm vyskytuje nově zavedená číslice \mathrm D? Výskyty v rámci jednoho čísla se počítají odděleně, takže například \mathrm{DD} přispívá do součtu dvakrát.
321
47 J / 47 S
Do čtverce ABCD je vepsána kružnice \omega, která se čtverce dotýká v bodech W, X, Y, Z ležících postupně na stranách AB, BC, CD, DA. Nechť E je vnitřní bod kratšího oblouku kružnice \omega mezi W a X a dále F průsečík BC a EY. Určete obsah trojúhelníku FYC, jestliže víte, že |EF| = 5 a |EY| = 7,
21
48 J / 48 S
V kryptogramu označují různá písmena různé číslice. Navíc je dáno \operatorname{S}(WE)=11, \operatorname{S}(LIKE)=23 a \operatorname{S}(NABOJ)=19, kde \operatorname{S}(n) značí ciferný součet přirozeného čísla n. Žádné ze tří čísel nezačíná nulou. Najděte pěticiferné číslo NABOJ.
60\,724
49 J / 49 S
Najděte všechna přirozená čísla n, pro která je součet všech jejich vlastních dělitelů roven 63.
Poznámka: Vlastní dělitel d čísla n splňuje 1 < d < n.
56, 76, 122
50 J / 50 S
Honza má mazácké auto se čtvercovými zadními koly (přední kola jsou standardní, tj. kulatá). Jezdit v takovém autě by bylo za normálních okolností dosti nepříjemné, ovšem Honza si na zadní kola nainstaloval velmi dobré tlumiče, díky nimž auto při jízdě po rovné silnici zůstává rovnoběžně s povrchem. Hrana zadního kola má délku 40\,\text{cm} a zadní náprava je vzhledem k autu pohyblivá pouze ve vertikálním směru. Jaký je poloměr předního kola (v cm), víme-li, že když se auto pohybuje konstantní rychlostí kupředu, zadní je náprava přesně polovinu času níže (blíž k silnici) a polovinu času výše (dál od silnice) než přední náprava?
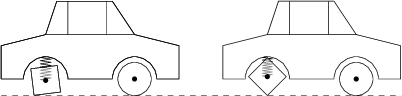
10 \sqrt{7}
51 J / 51 S
Město Budoucnosti má tvar pravidelného 2017úhelníku. Jeho vrcholy tvoří 2017 stanic metra, očíslovaných na plánku města od 1 do 2017 proti směru hodinových ručiček. Mají zde dvě linky metra, okrajovou a diagonální. Okrajová linka zajišťuje přímé spojení ze stanice a do stanice b (nikoli však v opačném směru), právě když a-b+1 je dělitelné 2017, a jedna taková jízda trvá 1 minutu. Diagonální linka zajišťuje přímé spojení ze stanice a do stanice b, právě když 2b-2a+1 je dělitelné 2017, a jedna taková jízda zabere 15 minut. Filip je nadšenec do metra a náruživý cestovatel. Rád by se ze stanice 1 dostal co nejdál, tj. do stanice, pro niž je optimální čas potřebný k jejímu dosažení nejdelší možný. Která čísla stanic splňují Filipovu podmínku?
1984, 1985
52 J / 52 S
Nechť f(n) značí počet přirozených čísel, která mají právě n cifer a jejichž ciferný součet je 5. Určete, kolik z 2017 čísel f(1), f(2), \dots, f(2017) má na místě jednotek jedničku.
202
53 J / 53 S
Na obrázku jsou dva nepřímo podobné šestiúhelníkové útvary, jejichž některé strany mají délky a, b, c, d, respektive A, B, C, D. Přiložíme-li tyto dva útvary k sobě, jak ukazuje obrázek, dostaneme nový šestiúhelníkový útvar podobný oběma menším (přímo podobný tomu napravo). Určete poměr A : a.
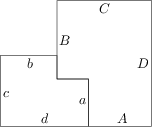
\sqrt{\frac{1+\sqrt 5}{2}}
54 J / 54 S
Najděte všechny dvojice kladných celých čísel (a,b), pro něž má každá z rovnic dva kladné celé kořeny.
(2,2), (6,6), (7,8), (8,7)
55 J / 55 S
Trojúhelníku ABC se stranami délek |AB| = 3, |BC| = 7 a |AC| = 5 je opsána kružnice \omega. Osa úhlu BAC protíná stranu BC v bodě D a kružnici \omega v bodě E. Nechť \gamma je kružnice nad průměrem DE. Druhý průsečík kružnic \omega a \gamma (různý od E) označme F. Určete |AF|.
\frac{30}{\sqrt{19}}
56 J / 56 S
Určete počet uspořádaných trojic (x, y, z), kde x, y, z jsou nezáporná celá čísla menší než 2017 a výraz je dělitelný 2017.
2017^2 + 1 = 4\,068\,290
57 J / 57 S
Bára s Helčou střídavě házejí běžnou hrací kostkou, která má dvě stěny červené, dvě zelené a dvě modré. Po každém hodu dostane hráčka žeton té barvy, kterou právě hodila. Vítězí ta z nich, která jako první shromáždí žetony všech tří barev. Bára začíná. S jakou pravděpodobností vyhraje?
81/140
58 J / 58 S
Najděte největší celé číslo n, pro něž má rovnice celočíselné řešení (k, n).
104
59 J / 59 S
Pizzerie pana Čtvrtníčka dodává své zboží ve speciálních pětiúhelníkových krabicích, které jsou vhodné jak pro jednu čtvrtinu velké pizzy, tak i pro tři čtvrtiny pizzy malé (viz obrázek). Jaký je poloměr malé pizzy v centimetrech, jestliže ta velká má poloměr 30\,\text{cm}?
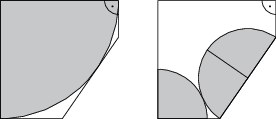
5(1+\sqrt{7}-\sqrt{2\sqrt{7}-4})






















