1 J
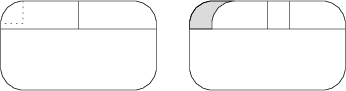
Egy régi villamos ablakai úgy néznek ki, mint az ábrákon. Minden sarok lekerekített része egy negyedkör 10,\text{cm}-es sugárral. A csúsztatható felső rész 10 centiméterrel van eltolva, ahogy a második ábrán látható. A nyitott rész magassága 13 cm. Mekkora a nyílás területe cm^2-ben?
130
2 J
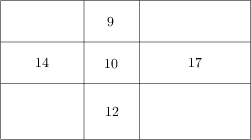
Egy téglalapot felosztottunk kilenc kisebb téglalapra az ábrán látható módon. Az egyes kis téglalapokba írt számok az adott kis téglalap kerületét jelentik. Adjuk meg a nagy téglalap kerületét.
42
3 J
Péter kitörölte egy négyjegyű prím egyik számjegyét és így 630-at kapott. Mi volt ez a prímszám?
6301
4 J
Patrícia, a sztárépítész egy nagyon modern ötszög alakú házat épít egy téglalap alakú telken. A telek oldalai 35\, \mbox{m} és 25\, \mbox{m} hosszúak. A ház alaprajza az ábrán látható módon passzol a telekre:
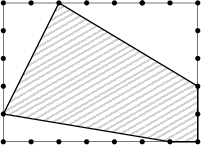
(A határokon a pontok 5 méteres távolságot jelölnek). A telek hányadrészét fedi le a ház?
\frac{41}{70}
5 J
Egy 16 pontból álló négyzetrács (mint az ábrán) tartalmazza 9 darab 1\times 1-es négyzet csúcsait, négy darab 2\times 2-es négyzet és egy darab 3\times 3-as négyzet csúcsait. Ez összesen 14 olyan négyzet amelyeknek az oldalai párhuzamosak a rács oldalaival. Mi a legkevesebb számú pont amelyeket kitörölve mind a 14 négyzetnek hiányzik legalább egy csúcsa?

4
6 J
Adjátok meg az négyzetösszeg egyes helyiértéken álló számjegyét.
5
7 J
Fejezzük ki a hányadost \dfrac{a}{b} alakú törtként a lehető legkisebb a és b pozitív egészekkel.
Megjegyzés: A felülvonás azt jelöli, hogy a tizedesjegyek periodikusan ismétlődnek, például 0,\overline{123} = 0,123123\ldots.
\frac{11}{12}
8 J
Passauban egy vasútállomás háromszöget formáz. Anna, Boris és Cathy megfigyelik a vonatforgalmat rendre Linzben, Regensburgban és Waldkirchenben a Passauból jövő sínek mentén. Anna 190, Boris 208, Cathy pedig 72 bejövő és kimenő vonatot számolt összesen. Hány vonat ment Linzből Regensburgba vagy Regensburgból Linzbe, ha semelyik vonatnak sem kiinduló vagy végállomása Passau, és nem is fordulhat vissza Passauban?
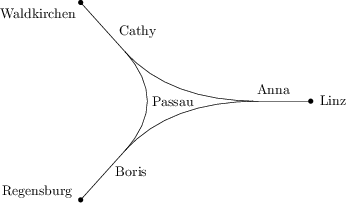
163
9 J
Adjuk meg az összes olyan x < 10\,000 pozitív egész számot, amelyre x egy páros szám negyedik hatványa, és permutálni tudjuk x számjegyeit úgy, hogy egy páratlan szám negyedik hatványát kapjuk. A számjegycsere után kapott szám nem kezdődhet nullával.
256
10 J
Az ABCD paralelogrammában egy C-n átmenő egyenes az AB oldalt egy E pontban metszi, úgy hogy EB =\frac 15\, AE. A CE szakasz a BD átlót az F pontban metszi. Adjuk meg a BF : BD arányt.
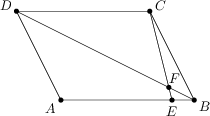
1 : 7
11 J / 11 S
Egy nagy társasházban 100 számozott lakás található. Minden lakásban egy, kettő vagy három ember lakik. Az elsőtől az 52-edik lakásig összesen 56 ember lakik, az 51-ediktől a 100-adik lakásokban pedig összesen 150 ember. Összesen hányan élnek a házban?
200
12 J / 12 S
Miklós leírta a 3-as számot piros ceruzával és a 2-es számot zöld ceruzával egy papírra. Ez volt az első lépés. Minden további lépésben pirossal leírta az előző lépésbeli két szám összegét, és zölddel a (pozitív) különbségüket. Milyen számot írt le pirossal a 2017. lépésben?
3 \cdot 2^{1008}
13 J / 13 S
Piroska a Négyszögletű-erdő bejáratánál áll. Az A pontból indulva el kell jutnia B-be, amilyen gyorsan csak lehet. Egy lehetőség az erdő széle mentén sétálni, ami összesen 140 m lenne. Persze tudja a háromszög-egyenlőtlenségből, hogy egy egyenes út rövidebb volna. De sajnos csak az ábrán látható cikkcakkos út van. Ha Piroska tudná, hogy ez az út rövidebb mint 140 m, akkor meg merné kockáztatni az átvágást. Adjuk meg a cikkcakkos út hosszát!
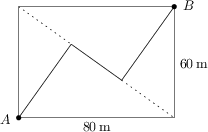
124\,\text{m}
14 J / 14 S
A nyolcjegyű palindrom számok \overline{abcddcba} alakúak, ahol a, b, c és d nem feltétlen különböző számjegyek. Hány olyan nyolcjegyű palindrom szám van, amiből törölhetünk néhány számjegyet úgy, hogy a törlés után megmaradó szám 2017 legyen?
8
15 J / 15 S
Egy n egész szám számjegyeinek összegét jelöljük \operatorname S(n)-nel, a számjegyeinek szorzatát pedig \operatorname P (n)-nel. Hány olyan pozitív egész n van, amelyre n = \operatorname S (n) + \operatorname P (n)?
9
16 J / 16 S
Egy gyár tulajdonosa 100 embert foglalkoztat. Minden csoportvezető havi fizetése 5\,000 €, minden szerelőé 1\,000 € és minden részmunkaidős munkásé 50 €. Összesen a tulajdonos havi 100\,000 Eurót fizet a dolgozóknak, és mindhárom típusból van legalább egy dolgozó. Hány csoportvezető dolgozik ennél a gyárnál?
19
17 J / 17 S
Az alábbi mozaik szabályos sokszögekből áll. A hatszög és a sötét háromszög köréírt köre megegyezik. Feltéve, hogy egy csíkos háromszög területe 17, határozzátok meg a sötét háromszög területét.
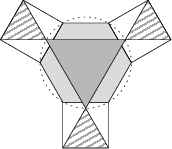
51
18 J / 18 S
A passaui vasútállomás felújítása során speciális mintázatú burkolatot akarnak a látássérült emberek számára létrehozni. A kövezet ábrája a lenti ábrán található. Sajnos csak 1\times 2-es csempék állnak rendelkezésre. Hányféleképpen lehet a burkolatot lefedni velük? A csempék megkülönböztethetetlenek, és két csempézést akkor tekintünk különbözőnek, ha bennük a csempék valamely ponton eltérő helyzetben vannak.
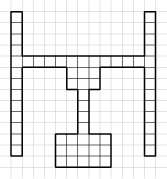
15
19 J / 19 S
Misi gondolt egy n pozitív egész számra. Ezután kiválaszotta n egy pozitív osztóját, megszorozta 4-gyel, majd kivonva ezt a számot n-ből 2017-et kapott eredményül. Adjátok meg az összes lehetséges számot, amire Misi gondolhatott.
2021, 10085
20 J / 20 S
Grizsa és Vanyecska nagyon jó barátok, így mindig elkezdenek csevegni, ha egymás mellé ülnek. Öt diák (Grizsát és Vanyecskát is beleértve) szeretne egy konstruktív kerekasztal beszélgetést, vagyis öt székre akarnak leülni egy körasztal mentén úgy, hogy Grizsa és Vanyecska ne legyenek szomszédok. Hányféleképpen tudják ezt megtenni? A forgatással egymásba vihető elrendezések is különbözőnek számítanak.
60
21 J / 21 S
Az ábrán AB egy M középpontú kör átmérője. D és C pontok úgy illeszkednek a körre, hogy AC\perp DM és MAC \sphericalangle = 56^\circ. Adjátok meg az AC és BD által bezárt hegyesszög nagyságát.
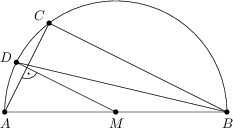
73^\circ
22 J / 22 S
Egy egységnégyzetekből felépülő alakzat úgy épül fel, hogy egy négyzetből kiindulva minden lépésben az aktuális állapot egy-egy példányát illeszti maga mellé az ábrának megfelelő módon. Milyen hosszú a vastaggal jelölt határolóvonal a hatodik állapotban?
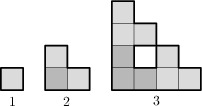
488
23 J / 23 S
Egy hatalmas kerekasztal körül 2017 széket helyeztek el, a székeken szuperhősök és főgonoszok ülnek. A szuperhősök mindig igazat mondanak, míg a főgonoszok mindig hazudnak. Valamennyi, az asztalnál ülő személy kijelentette, hogy egy szuperhős és egy főgonosz között foglal helyet. Utólag azonban kiderült, hogy valamiért pontosan egy szuperhős tévedett ezt illetően. Hány szuperhős ül az asztalnál?
1345
24 J / 24 S
Találjátok meg az összes pozitív valós x-et, amelyre
\sqrt[2016]{2017}
25 J / 25 S
Leo egy szabályos dodekaéder éleit akarja kiszínezni a következő módon: kiválaszt egy színes filctollat, majd az egyik csúcsból kiindulva a filctoll felemelése nélkül sorra kiszínez éleket úgy, hogy semelyik élt nem színezi ki kétszer, ezt az eljárást addig folytatja, ameddig tudja. Ezután elővesz egy másik színű filctollat, majd kezdve egy még ki nem színezett éllel az előzőekben leírtakat követi ismét. Ezt addig folytatja, amíg a dodekaéder minden éle ki nincs színezve pontosan egy színnel. Legalább hány filctoll használata szükséges?
Megjegyzés: A szabályos dodekaéder olyan test, melynek tizenkét ötszöglapja van, ahogy azt az ábra is mutatja:
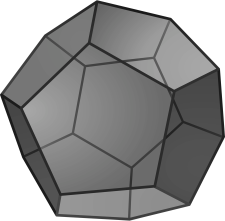
10
26 J / 26 S
Joci, a tájépítész tervezett egy murvával felszórt utat, mely egy tavat kerül meg. Az ABC háromszög jelöli az út közepét, ennek pedig rendre a = 80\,\text{m}, b = 100\,\text{m} és c = 120 \,\text{m} hosszú oldalai vannak. Az út széleinek ettől a háromszögtől való távolsága 1\,\text{m}. Hány \text{m}^3 murvát kell Jocinak rendelnie, ha átlagosan 4\,\text{cm} a murvaréteg vastagsága?
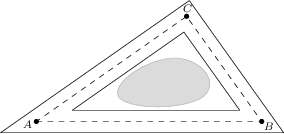
24
27 J / 27 S
Adjuk meg az összes négyjegyű négyzetszámot amelynek az első két számjegye egyenlő, és a két utolsó számjegye szintén egyenlő.
7744
28 J / 28 S
A vidámparkban van egy lottósorsolás a következő szabályokkal: a résztvevőnek négy megkülönböztethetetlen doboz közül kell egyet választania, és abból egy golyót kihúznia. Ha a golyó fehér, a résztvevő nyert, ha fekete, vesztett. Például, ha a golyók eloszlása a négy dobozban ahol minden (w, b) pár egy dobozt jelöl, amiben w fehér és b fekete golyó van, a játékos \frac{5}{8} eséllyel nyer. Minden 1000. résztvevő megnyeri a szuper jokert: tetszőlegesen újraoszthatja a golyókat az egyes dobozok közt. Ezek után a dobozokat összekeverik, és a résztvevő választhat egy dobozt, amiből húz egyet. Johanna egy szerencsés lány, és megnyerte ezt a szuper jokert. Mekkora a legnagyobb valószínűség, amit a példában szereplő eloszlásból kiindulva érhet el ideális stratégiával?
\frac{51}{58}
29 J / 29 S
Egy autóbusz, egy kamion és egy motorbicikli állandó sebességgel haladnak, majd ebben a sorrendben, egyenlő időközönként elmennek egy traffipax mellett. Az úton később egy újabb traffipax mellett haladnak el, szintén azonos időközönként (ráadásul ugyanannyi idővel váltják egymást, mint az első traffipax esetén), ám ezúttal más sorrendben: autóbusz, motorbicikli, kamion. Határozzátok meg az autóbusz sebességét, ha a kamion sebessége 60\,\text{km/h}, a motorbiciklié pedig 120\,\text{km/h}.
80\,\text{km/h}
30 J / 30 S
Keressük meg az összes számhármast a következő állításban szereplő lyukak pozitív egészekkel való betöltésére, úgy, hogy az állítás igaz legyen: „Ebben az állításban, \boxed{\phantom{00}}\,\%-a a számjegyeknek nagyobb mint 4, \boxed{\phantom{00}}\,\%-a a számjegyeknek kisebb mint 5, és \boxed{\phantom{00}}\,\%-a a számjegyeknek vagy 4, vagy 5”.
50, 50, 60
31 J / 31 S
Pali marhái egy háromszög alakú réten legelnek, jelöljük ezt ABC-vel. Mivel a pöttyös és egyszínű tehenei nem jönnek ki jól egymással, Pali épített egy húszméteres kerítést, az AC oldalra merőlegesen, a P pontból kiindulva, aminek a másik vége a B pontba került. Ez a kerítés a rétet két derékszögű háromszögre osztotta. A kerítés ellen az A pont körül legelő pöttyös tehenek hamar elkezdtek tiltakozni, rámutatva, hogy AP : PC = 2 : 7, és egy tisztességesebb elosztást követeltek. Ezután Pali kicserélte a kerítést egy, az előzővel párhuzamos másikra, ami hasonlóan a rét határainál ér véget, de két egyenlő területű részre osztja a rétet. Mi az új kerítés hossza méterben?
30 \sqrt{\frac27}
32 J / 32 S
Egy táblán öt, egymástól nem feltétlenül különböző valós szám állt. Minden lehetséges számpár esetén Wendy kiszámolta a számpárok tagjainak összegét, majd felírta az így kapott tíz számot a táblára: valamint letörölte a korábbi számokat. Határozzátok meg a letörölt számok szorzatának összes lehetséges értékét.
-144
33 J / 33 S
Írjátok fel 333-at különböző páratlan pozitív egészek négyzetösszegeként.
3^2 + 5^2 + 7^2 + 9^2 + 13^2
34 J / 34 S
Zsuzsi kiválasztott 3 valós számot: a, b, c, majd bevezette a \odot műveletet: x \odot y = ax + by + cxy. Példaképpen kiszámította, hogy 1 \odot 2 = 3 és 2 \odot 3 = 4. Ezután észrevette, hogy létezik egy nullától különböző u valós szám, amelyre z \odot u = z minden valós z szám esetén. Mennyi u értéke?
4
35 J / 35 S
Egy egyenes és négy kör: három közülük egyaránt r sugarú, egy pedig 1 sugarú, az ábrának megfelelően helyezkedik el a síkon. Határozzátok meg r-et.
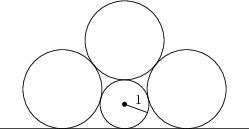
\frac{1+\sqrt{5}}{2}
36 J / 36 S
Valaki egy betonfalra graffitizett öt, nem feltétlenül különböző valós számot, melyek összege 20. Kincső kiszámította ezen öt szám közül kiválasztott számpárok összegének alsó egészrészét valamennyi lehetséges számpár esetén (tehát a nála nem nagyobb egész számok közül a maximálisat), így tehát tíz egész számot kapva eredményül. Végezetül összeadta az így kapott számokat. Mi a legkisebb érték, amit Kincső eredményül kaphatott?
72
37 J / 37 S
Valamely n pozitív összetett egész szám esetén \xi(n) jelölje n három legkisebb pozitív osztójának összegét, \vartheta(n) pedig n két legnagyobb pozitív osztójának összegét. Találjátok meg az összes n összetett számot, amelyre \vartheta(n)=(\xi(n))^4 teljesül.
864
38 J / 38 S
Egy 3 \times 3-as tábla bal alsó sarkában egy kisegér üldögél. A tábla jobb felső sarkában egy darabka sajt van, az egér ezt akarja megszerezni, de csak egyesével tud haladni a tábla szomszédos mezőin. (Csak a közös oldallal rendelkező négyzetek szomszédosak.) Hányféleképp tudunk úgy akadályokat elhelyezni a tábla valahány (esetleg nulla) korábban üres mezőjén úgy, hogy az egér továbbra is elérjen a sajthoz?
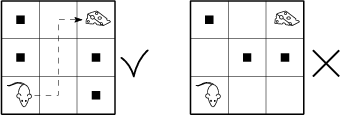
51
39 J / 39 S
Valamennyi (x, y) valós számpár közül, amely kielégíti a következő egyenletet: legyen (x_0, y_0) olyan, melyre x_0 minimális. Mennyi lehet y_0?
-3
40 J / 40 S
Legyen \triangle ABC derékszögű háromszög, melynek C a derékszögű csúcsa. Legyenek D és E belső pontjai az AB szakasznak úgy, hogy a D pont A és E között helyezkedik el, továbbá CD és CE harmadolják az ACB \sphericalangle szöget. Amennyiben DE:BE = 8:15, találjuk meg \tan ABC \sphericalangle értékét.
\frac{4\sqrt3}{11}
41 J / 41 S
Máté a következő játékot játssza: Egy egész számot kell kitalálnia 1 és N között, beleértve a végpontokat. Minden lépésben megnevez egy számot; ha ez épp a kitalálandó szám, a játék véget ér, máskülönben elárulják neki, hogy a tippje nagy vagy kicsi volt. Amennyiben a tippje túl nagy volt, be kell fizetnie 1 €-t, ha pedig túl kicsi, úgy a fizetendő összeg 2 € (pontos találat esetén nem kell fizetnie). Melyik az a legnagyobb N egész, amelyre teljesül, hogy Máté mindig be tudja a játékot fejezni legfeljebb 10 € költéssel?
232
42 J / 42 S
a, b, c pozitív egészek, hogy a \geq b \geq c és Találjátok meg a összes lehetséges értékét.
134
43 J / 43 S
Egy földönkívüliek által használt űrhajónak tökéletes gömb alakja van, melynek sugara R, illetve három párhuzamos, 1 űm (űrlény méter) hosszú, elhanyagolható szélességű egyenes rúd támasztja függőlegesen. Ezeknek a lábaknak az alsó vége egy 9 űm oldalhosszúságú szabályos háromszöget határoz meg, és ha az űrhajó sík terepen nyugszik, a gömb pont érinti a talajt. Mekkora az űrhajó R sugara (űrlény méterben kifejezve)?
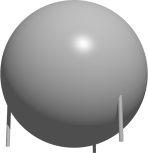
14
44 J / 44 S
Négy testvér, Ádám, Balázs, Csilla és Dani, rengeteg mogyorót gyűjtöttek össze az erdőben. Éjjel Ádám mókuséhesen ébredt, így nem bírta megállni, hogy egyen néhányat a mogyorókból. Miután összeszámolta a mogyorókat, arra jutott, hogy ha eggyel kevesebb mogyoró lenne, négy egyenlő részre lehetne osztani a maradékot. Így tehát félretett egyet, majd megette a részét (vagyis a maradék egynegyedét); majd visszafeküdt aludni. Az éjszaka folyamán később Balázs is felébredt a gyomra korgására, és ő is úgy számolta, hogy egy mogyorót félretéve elnegyedelheti a maradékot, majd megette a rá eső negyedet. Az éjszaka folyamán aztán ugyanígy járt el Csilla és Dani is. Miután mind felkeltek reggel, újfent megszámolták a megmaradt mogyorókat, és megint csak azt fedezték fel, hogy egyet félretéve a maradékot fel tudják osztani négy egyenlő részre. Minimálisan hány mogyorót gyűjtöttek össze a testvérek?
1021
45 J / 45 S
Egy pozitív egész számot kellemesnek nevezünk, ha minden prímosztója 2, 3, és 7 közül kerül ki. Hány kellemes szám van az 1000, 1001, \dots, 2000 számok között?
19
46 J / 46 S
Decimus császár betiltotta a 0 számjegy használatát (amit elődje, Nullus vezetett be) és bevezette helyette a \mathrm D szimbólumot, ami a tízes számjegynek felel meg. Minden pozitív egész szám egyértelműen kifejezhető így, például Az átállás megkönnyítése végett összeírtak egy listát, ami minden egész számot tartalmaz 1-től \mathrm{DDD}-ig. Hányszor szerepel az új számjegy, \mathrm D a listán? Ha egy számnak több \mathrm D számjegye is van, azt annyiszor számoljuk, ahányszor előfordul.
321
47 J / 47 S
Az ABCD négyzet beírt köre \omega, ez a négyzet oldalait a W, X, Y, Z pontokban érinti, melyek rendre az AB, BC, CD, DA oldalakon helyezkednek el. Legyen E egy belső pontja az \omega kör W és X közé eső (rövidebb) ívének, és legyen F a BC és EY egyenesek metszéspontja. Feltéve, hogy EF = 5 és EY = 7, határozzátok meg FYC háromszög területét.
21
48 J / 48 S
A fenti egyenletben különböző betűk különböző számjegyeket jelölnek. Továbbá tudjuk, hogy \operatorname{D}(W\kern-.1emE)= 11, \operatorname{D}(LIKE)=23 és \operatorname{D}(N\kern-.2emABOJ)=19, ahol \operatorname{D}(n) tetszőleges pozitív egész n esetén n számjegyeinek összegét jelöli. A három szám egyike sem nullával kezdődik. Adjátok meg az ötbetűs N\kern-.2emABOJ szó értékét.
60\,724
49 J / 49 S
Találjátok meg az összes pozitív egész n számot, melynek valódi osztóinak s összege 63.
d valódi osztója n-nek, ha osztója n-nek és 1 < d < n teljesül.
56, 76, 122
50 J / 50 S
Robinak menő kocsija van négyzet alakú hátsó kerekekkel (az első kerekeknek a szokásoknak megfelelően kör alakjuk van). Egy ilyen autót meglehetősen kényelmetlen lenne vezetni, de Robi kitűnő lengéscsillapítóról gondoskodott a hátsó kerekek miatt, így az autó a sík terepen haladva végig a talajjal párhuzamos helyzetű maradhat. A hátsó kerekek oldalhossza 40\,\text{cm}. Mekkora az elülső kerekek sugara (cm-ben kifejezve), ha tudjuk, hogy amikor az autó egyenletes sebességgel halad előre, a hátsó kerekek tengelye pontosan annyit tartózkodik az első kerekek tengelye fölött, mint alatt?
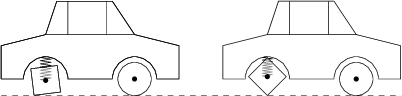
10 \sqrt{7}
51 J / 51 S
A jövő városa szabályos 2017-szög alakú. A város csúcsaiban 2017 metrómegálló van, melyeknek 1, 2, \ldots, 2017 a nevei, az óramutató járásával ellentétesen, a város térképét nézve. Két metróvonal van: Oldal és Átló. Az Oldal nevű metróvonal közvetlenül közlekedik a megállóból b megállóba (de visszafele nem) pontosan akkor, ha a-b+1 osztható 2017-tel, továbbá egy megállót 1 perc alatt tesz meg. Az Átló nevű metróvonal közvetlenül elmegy a megállóból b-be pontosan akkor, ha 2b-2a+1 osztható 2017-tel, és egy ilyen megálló megtétele 15 percig tart. Tibi nagyon szeret metróval utazni. Kiindulva az 1-es megállóból, el szeretne jutni egy n jelzésű megállóba, ami a következőt teljesíti: ha minden megállóhoz tekintjük az 1-ből odavezető, legkisebb összidejű utat, akkor ezek közül az n-be vivő a lehető leghosszabb. Adjátok meg az összes ilyen n lehetséges úticél megállóhelyet Tibi számára.
1984, 1985
52 J / 52 S
Legyen f(n) azon n jegyű pozitív egészek száma, melyek számjegyeinek összege 5. Számítsátok ki, hogy az f(1), f(2), \dots, f(2017) számok közül mennyi végződik az 1-es számjegyre.
202
53 J / 53 S
Az ábrán két, középpontosan hasonló hatszög látható, melyek bizonyos oldalhosszai rendre a, b, c, d és A, B, C, D. Ha ezt a két alakzatot az ábrának megfelelően összeillesztjük, egy, a két kisebb hatszöghöz hasonló hatszöget kapunk (mely irányítástartóan hasonló a jobb oldali hatszöghöz). Találjátok meg a p=\frac{A}{a} arányszámot.
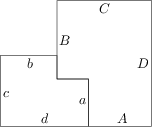
\sqrt{\frac{1+\sqrt 5}{2}}
54 J / 54 S
Határozzuk meg az összes (a,b), pozitív egész számpárt, ha az alábbi egyenletek minden gyöke szintén pozitív egész.
(2,2), (6,6), (7,8), (8,7)
55 J / 55 S
ABC háromszög köréírt köre \omega, a háromszög oldalai pedig AB = 3, BC = 7, és AC = 5. Az A-nál lévő szög szögfelezője a BC oldalt a D pontban metszi, míg az \omega kört E-ben. Legyen \gamma a DE-re mint átmérőre emelt kör. Az \omega és \gamma körök egymást E és F pontokban metszik. Számítsátok ki az AF szakasz hosszát.
\frac{30}{\sqrt{19}} = \frac{30\sqrt{19}}{19}
56 J / 56 S
Határozzátok meg az (x, y, z) rendezett számhármasok számát, ahol x, y, z olyan 2017-nél kisebb nemnegatív egész számok, melyekre osztható 2017-tel.
2017^2 + 1 = 4\,068\,290
57 J / 57 S
Juli és Tamás játszanak egy szabályos dobókockával, amelynek két oldala pirosra, két oldala zöldre és két oldala kékre van festve. Felváltva dobnak a kockával, addig amíg valamelyikük nem látta már mindhárom színt a saját körei alatt. Ez a játékos győz. Mekkora a valószínűsége, hogy Juli győz, ha ő dob először?
81/140
58 J / 58 S
Adott a következő egyenlet: határozzátok meg a legnagyobb n egész számot, amelyre létezik (k, n) egész megoldás.
104
59 J / 59 S
A Quarter-Pizzéria egyedi, ötszög alakú pizzásdobozokban szállítja ki a pizzáit, amelyben éppen elfér egy negyed nagy pizza, vagy háromnegyed kis pizza (az ábrán látható módon). Mekkora a kis pizza sugara, ha a nagy pizzáé 30 cm?
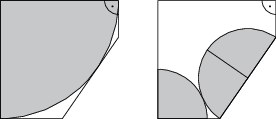
5(1+\sqrt{7}-\sqrt{2\sqrt{7}-4})\,\text{cm}