1 J
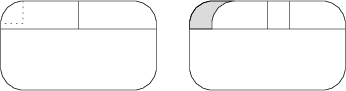
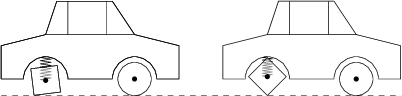
Okna w starym tramwaju mają kształt przedstawiony na pierwszym rysunku. Wszystkie cztery zaokrąglenia rogów to ćwiartki okręgu o promieniu 10\ \text{cm}. Okno zostało uchylone poprzez przesunięcie lewego górnego segmentu o 10\ \text{cm} w prawo, jak pokazano na drugim rysunku. Wysokość przesuniętego segmentu jest równa 13\ \text{cm}. Ile wynosi, w \text{cm}^2, pole powierzchni otwartego fragmentu okna (oznaczonego szarym kolorem)?
130
2 J
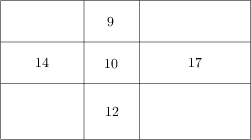
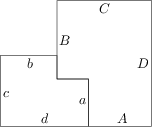
Prostokąt został podzielony na dziewięć mniejszych prostokątów w sposób pokazany na rysunku. Wewnątrz pięciu z nich napisano ich obwody. Znajdź obwód dużego prostokąta.
42
3 J
Piotr usunął jedną cyfrę z czterocyfrowej liczby pierwszej i otrzymał 630. Jaka była wyjściowa liczba pierwsza?
6301
4 J
Jarek, największa gwiazda wśród architektów, chce zbudować bardzo nowoczesną pięciokątną willę na prostokątnej posesji o wymiarach 35\ \text{m}\times 25\ \text{m}. Powierzchnia działki przeznaczona na budowę jest zaznaczona na rysunku:
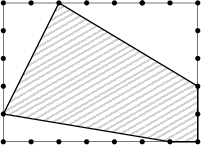
(Kolejne kropki na brzegu wyznaczają odległości 5\ \text{m}.) Jaką część powierzchni posesji zajmuje pięciokąt, na planie którego zostanie zbudowana willa?
41/70
5 J
Kwadratowa siatka (widoczna na rysunku) składająca się z 16 kropek zawiera wierzchołki dziewięciu kwadratów o wymiarach 1\times 1, czterech 2\times 2 i jednego 3\times 3, co daje 14 kwadratów o bokach równoległych do krawędzi siatki. Jaka jest najmniejsza liczba kropek, które można usunąć w taki sposób, żeby każdemu z tych 14 kwadratów brakowało co najmniej jednego wierzchołka?

4
6 J
Znajdź cyfrę jedności liczby
5
7 J
Zapisz iloraz w postaci ułamka nieskracalnego \dfrac{a}{b} (gdzie a i b są całkowite dodatnie).
Uwaga. Powyższy zapis oznacza ułamek dziesiętny okresowy, np. 0,(123) = 0,123123\ldots.
11/12
8 J
Stacja kolejowa w Sosnowcu ma kształt trójkąta. Karolina, Jurand i Bercik obserwują ruch pociągów kursujących przez Sosnowiec odpowiednio w Katowicach, Jaworznie i Będzinie. Karolina naliczyła 190, Jurand — 208, a Bercik — 72 pociągi w obu kierunkach. Ile pociągów odbyło kurs na trasie Katowice–Jaworzno (w którymkolwiek kierunku)? Zakładamy, że żaden pociąg nie zaczyna ani nie kończy swojego biegu w Sosnowcu i żaden pociąg w nim nie zawraca.
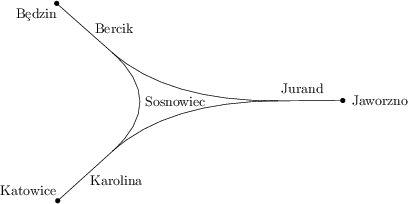
163
9 J
Znajdź wszystkie takie dodatnie liczby całkowite x<10000, że x jest czwartą potęgą pewnej liczby parzystej oraz można przestawić cyfry liczby x tak, aby otrzymać czwartą potęgę pewnej liczby nieparzystej (przyjmujemy, że zapis liczby w systemie dziesiętnym nie może zaczynać się cyfrą 0).
256
10 J
W równoległoboku ABCD prosta przechodząca przez punkt C przecina bok AB w punkcie E, przy czym EB =\frac 15\, AE. Odcinek CE przecina przekątną BD w punkcie F. Znajdź stosunek BF : BD.
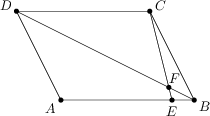
1 : 7
11 J / 11 S
W budynku jest 100 ponumerowanych mieszkań. Każde z nich ma jednego, dwóch lub trzech lokatorów. Łączna liczba mieszkańców lokali od 1 do 52 jest równa 56, a łączna liczba mieszkańców lokali od 51 do 100 jest równa 150. Ile osób mieszka w tym budynku?
200
12 J / 12 S
W pierwszym kroku Mikołaj napisał na kartce liczbę 3 pistacjową kredką oraz liczbę 2 limonkową kredką. W każdym następnym kroku napisał na kartce sumę liczb z poprzedniego kroku na pistacjowo, natomiast na limonkowo ich (dodatnią) różnicę. Jaką liczbę napisał na pistacjowo w 2017 kroku?
3 \cdot 2^{1008}
13 J / 13 S
Czerwony Kapturek stoi i myśli przy wejściu do „Prostokątnego Lasu”. Zaczynając z punktu A chce ona dotrzeć do punktu B najszybciej, jak to możliwe. Jedną z możliwości jest spacer skrajem lasu o łącznej długości 140\ \text{m}. Oczywiście Kapturek zna nierówność trójkąta i wie, że droga po przekątnej lasu byłaby najkrótsza, ale niestety przez las wiedzie tylko przedstawiona na rysunku droga w kształcie zygzaka z dwoma zakrętami o 90^\circ. Gdyby Kapturek wiedziała, że ta droga jest krótsza niż 140\ \text{m}, chętnie skorzystałaby ze skrótu… Jaka jest długość (w metrach) zygzaka prowadzącego przez las?
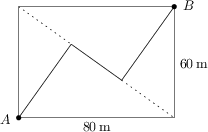
124
14 J / 14 S
Ośmiocyfrowym palindromem nazywamy każdą liczbę postaci \overline{abcddcba}, gdzie a, b, c, d są cyframi (niekoniecznie różnymi). Ile różnych ośmiocyfrowych palindromów ma tę własność, że po usunięciu z nich pewnych cyfr można otrzymać liczbę 2017?
8
15 J / 15 S
Dla dowolnej dodatniej liczby całkowitej n przez \operatorname S(n) i \operatorname P(n) oznaczamy odpowiednio sumę i iloczyn cyfr liczby n. Ile dodatnich liczb całkowitych n ma tę własność, że n=\operatorname S (n) + \operatorname P (n)?
9
16 J / 16 S
Właściciel fabryki zatrudnia 100 pracowników — brygadzistów, robotników i stażystów (na każdym stanowisku pracuje przynajmniej jedna osoba). Miesięczne wynagrodzenie brygadzisty wynosi 5000 zł, robotnika 1000 zł, a stażysty 50 zł. Każdego miesiąca właściciel wypłaca swoim pracownikom łącznie 100\ 000 zł. Ilu brygadzistów jest zatrudnionych w tej fabryce?
19
17 J / 17 S
Poniższa mozaika składa się z wielokątów foremnych. Jasnoszary sześciokąt i ciemnoszary trójkąt są wpisane w ten sam okrąg. Wiedząc, że pole każdego z zakreskowanych trójkątów wynosi 17, znajdź pole ciemnoszarego trójkąta.
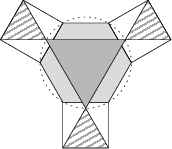
51
18 J / 18 S
W ramach renowacji dworca w Sosnowcu budowany jest specjalny chodnik z kostki brukowej przystosowany dla osób niedowidzących. Kształt chodnika jest przedstawiony na poniższym rysunku. Niestety, dostępne są jedynie kostki o wymiarach 1 \times 2. Na ile sposobów można wybrukować chodnik takimi kostkami? Kostki są nierozróżnialne. Dwa brukowania są uznawane za różne, jeśli w którymś miejscu kostki są ustawione w różnej pozycji.
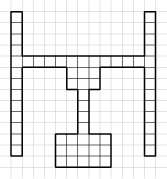
15
19 J / 19 S
Michał wybrał dodatnią liczbę całkowitą n. Następnie wybrał dodatni dzielnik n, pomnożył go przez 4 i otrzymany wynik odjął od n, uzyskując 2017. Znajdź wszystkie liczby, które mógł wybrać Michał.
2021, 10085
20 J / 20 S
Dominik i Tomek są dobrymi przyjaciółmi, więc kiedy tylko usiądą obok siebie, zaczynają rozmawiać. Pięcioro studentów, włączając Dominika i Tomka, chce odbyć konstruktywną dyskusję, więc chcą usiąść przy okrągłym stole w taki sposób, aby Dominik i Tomek nie siedzieli obok siebie. Ile jest możliwych usadzeń wokół stołu spełniających ten warunek? Przyjmujemy, że dwa usadzenia takie, że jedno z nich powstaje z drugiego przez obrót, są różne.
60
21 J / 21 S
W konfiguracji przedstawionej na rysunku odcinek AB jest średnicą okręgu o środku M. Punkty C i D leżą na tym okręgu, przy czym proste AC i DM są prostopadłe oraz \sphericalangle MAC=56^\circ. Znajdź miarę kąta ostrego między prostymi AC i BD (w stopniach).
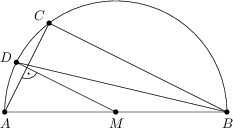
73^\circ
22 J / 22 S
Budujemy figurę złożoną z kwadratów jednostkowych poprzez sukcesywne sklejanie jej kopii, tak jak na poniższym rysunku. Jaka jest długość brzegu (na rysunku oznaczonego pogrubioną linią) figury otrzymanej w szóstym kroku?
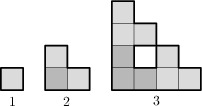
488
23 J / 23 S
Rycerze i łotrzy zajmują wszystkie 2017 miejsc przy bardzo dużym okrągłym stole. Rycerze zawsze mówią prawdę, a łotrzy zawsze kłamią. Każda osoba przy stole stwierdziła, że siedzi pomiędzy rycerzem a łotrem. Z niewiadomych powodów jeden rycerz się pomylił. Ilu rycerzy siedzi przy stole?
1345
24 J / 24 S
Znajdź wszystkie dodatnie liczby rzeczywiste x spełniające równanie
\sqrt[2016]{2017}
25 J / 25 S
Piotruś chce pokolorować krawędzie dwunastościanu foremnego w następujący sposób: wybiera pisak jednego koloru i zaczynając w dowolnym wierzchołku koloruje krawędzie bez odrywania ręki do momentu, aż chce lub musi się zatrzymać (każdą krawędź może pokolorować tylko raz). Następnie wybiera inny kolor i powtarza ten proces, używając różnych kolorów, aż każda krawędź będzie pokolorowana. Jaka jest minimalna liczba kolorów, których Piotruś musi użyć, żeby pokolorować dwunastościan foremny w taki sposób?
Uwaga. Dwunastościan foremny to wielościan o 12 ścianach w kształcie pięciokątów foremnych, jak pokazano na rysunku:
10
26 J / 26 S
Ogrodnik Andrzej zaprojektował żwirową drogę dookoła jeziora. Trójkąt ABC wyznacza środek drogi, a jego boki mają długości 80\ \text{m}, 100\ \text{m} oraz 120 \ \text{m}. Granice drogi są zawarte w prostych odległych o 1\ \text{m} od prostych zawierających boki trójkąta, jak pokazano na rysunku. Ile \text{m}^3 żwiru potrzebuje Andrzej, jeżeli chce, aby wysokość warstwy żwiru, z którego zostanie usypana droga, miała średnio 4\ \text{cm}?
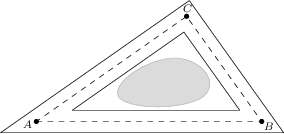
24
27 J / 27 S
Znajdź wszystkie liczby czterocyfrowe będące kwadratami liczb całkowitych, których dwie pierwsze cyfry są równe oraz dwie ostatnie cyfry są równe.
7744
28 J / 28 S
Podczas festynu urządzono loterię o następujących zasadach: uczestnik najpierw wybiera jedno z czterech nieodróżnialnych pudełek, a następnie losuje z wybranego pudełka jedną ze znajdujących się w nim kul. Jeżeli wylosowana kula jest biała, uczestnik wygrywa, a jeżeli czarna — przegrywa. Przykładowo, jeżeli początkowy rozkład kul w czterech pudełkach jest następujący gdzie każda z par (b,c) oznacza pudełko zawierające b białych oraz c czarnych kul, to uczestnik wygrywa z prawdopodobieństwem \frac{5}{8}. Dodatkową zasadą jest, że co tysięczny uczestnik otrzymuje super-jokera, czyli specjalny przywilej polegający na możliwości rozmieszczenia kul w pudełkach (co najmniej jednej w każdym) przed losowaniem zgodnie z własnym pomysłem. Następnie pudełka są mieszane, a uczestnik na normalnych zasadach wybiera jedno z nich i losuje kulę. Natalia ma dziś szczęście i właśnie otrzymała super-jokera. Jakie jest największe możliwe prawdopodobieństwo zwycięstwa, jakie Natalia może uzyskać, odpowiednio rozmieszczając kule z powyższego przykładu w pudełkach?
51/58
29 J / 29 S
Trzy pojazdy: autobus, ciężarówka i motocykl, z których każdy porusza się ze stałą prędkością, minęły stojącego nieruchomo przy ulicy obserwatora w tej właśnie kolejności, w równych odstępach czasu. Wkrótce później minęły one innego (stojącego dalej) obserwatora w równych odstępach czasu o tej samej długości, co za pierwszym razem, ale w innej kolejności: autobus, motocykl, ciężarówka. Znajdź prędkość autobusu (w \text{km/h}), jeżeli prędkość ciężarówki to 60\ \text{km/h}, a prędkość motocykla to 120\ \text{km/h}.
80
30 J / 30 S
Znajdź wszystkie sposoby wypełnienia luk w poniższym stwierdzeniu dodatnimi liczbami całkowitymi w taki sposób, aby stało się ono prawdziwe: „Spośród wszystkich cyfr występujących w niniejszym stwierdzeniu, dokładnie \boxed{\strut\quad}\% cyfr jest większych od 4, dokładnie \boxed{\strut\quad}\% cyfr jest mniejszych od 5 i dokładnie \boxed{\strut\quad}\% cyfr jest równych 4 lub 5.”
50, 50, 60
31 J / 31 S
Bydło Dominika jest wyprowadzane na łąkę w kształcie trójkąta ABC. Ponieważ jego łaciate krowy i te bez plam nie żyją w zgodzie, Dominik postanowił wybudować dwudziestometrowy płot prostopadły do boku AC zaczynając w punkcie P na AC, a kończąc w punkcie B, dzieląc całą łąkę na dwa trójkąty prostokątne. Jednakże łaciate krowy (żyjące w części z wierzchołkiem A) w proteście wskazały, że AP : PC = 2 : 7 i zażądały bardziej sprawiedliwego podziału. Dominik, postanowił więc zamienić wybudowany płot innym, równoległym do starego o końcach leżących na bokach łąki, lecz dzielący łąkę na dwie części o równych polach. Jakiej długości płot powinien wybudować Dominik?
30 \sqrt{2/7}
32 J / 32 S
Pięć liczb rzeczywistych (niekoniecznie różnych) napisano na tablicy. Dla każdej pary liczb, Łukasz obliczył ich sumę i napisał dziesięć wyników na tablicy, wymazując początkowe liczby. Wyznacz wszystkie możliwe wartości iloczynu wymazanych liczb.
-144
33 J / 33 S
Zapisz 333 jako sumę dowolnej liczby kwadratów różnych nieparzystych dodatnich liczb całkowitych.
3^2 + 5^2 + 7^2 + 9^2 + 13^2
34 J / 34 S
Agnieszka wybrała trzy liczby rzeczywiste a, b, c i zdefiniowała działanie \odot wzorem x\odot y=ax+by+cxy. W ramach ćwiczenia policzyła, że 1 \odot 2=3 oraz 2\odot 3=4. Po dłuższych rozważaniach doszła do wniosku, że istnieje niezerowa liczba rzeczywista u taka, że z \odot u=z dla dowolnej liczby rzeczywistej z. Wyznacz u.
4
35 J / 35 S
Trzy okręgi o promieniu r i okrąg o promieniu 1 są styczne do siebie i do prostej, jak pokazano na rysunku. Znajdź r.
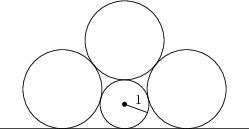
(1+\sqrt{5})/2
36 J / 36 S
Na starym betonowym murze ktoś umieścił matematyczne graffiti składające się z pięciu (niekoniecznie różnych) liczb rzeczywistych, których suma jest równa 20. Dla każdej pary spośród tych liczb Kamil obliczył ich sumę i zaokrąglił ją w dół (tj. do największej liczby całkowitej, która nie przekracza uzyskanej sumy), otrzymując w ten sposób dziesięć liczb całkowitych. W końcu dodał do siebie wszystkie te liczby. Jaka jest najmniejsza możliwa suma, którą mógł uzyskać?
72
37 J / 37 S
Dla dodatniej liczby całkowitej złożonej n oznaczmy przez \xi(n) sumę trzech najmniejszych dodatnich dzielników liczby n, a przez \vartheta(n) — sumę dwóch największych dzielników n. Znajdź wszystkie liczby złożone n, dla których \vartheta(n)=(\xi(n))^4.
864
38 J / 38 S
W lewym dolnym polu tablicy 3\times 3 znajduje się mysz, której celem jest dojście do sera znajdującego się w prawym górnym rogu, poruszając się tylko pomiędzy sąsiednimi polami. Na ile sposobów można umieścić przeszkody na niektórych wolnych polach tablicy (być może żadnym) w taki sposób, aby mysz wciąż mogła dotrzeć do sera?
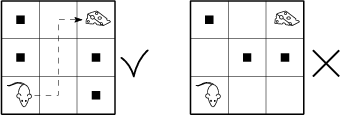
51
39 J / 39 S
Spośród wszystkich par liczb rzeczywistych (x, y) spełniających równość niech (x_0, y_0) będzie tą, w której x_0 jest możliwie najmniejsze. Znajdź y_0.
-3
40 J / 40 S
W trójkącie ABC kąt przy wierzchołku C jest prosty. Punkty D i E leżą na boku AB, przy czym punkt D leży między punktami A i E, oraz półproste CD i CE dzielą kąt ACB na trzy równe części. Znajdź AC:BC wiedząc, że DE:BE=8:15.
4\sqrt3/11
41 J / 41 S
Mikołaj gra ze starszym bratem w grę. Jego brat wybiera w tajemnicy liczbę całkowitą z przedziału od 1 do N (włącznie), a zadaniem Mikołaja jest jej odgadnięcie. W każdej turze Mikołaj wybiera pewną liczbę całkowitą. Jeśli trafił w tajemną liczbę brata, gra się kończy, w przeciwnym razie dostaje informację o tym, czy jego strzał jest większy, czy mniejszy od tajemnej liczby. Niestety, jego brat, korzystając z przewagi wieku, wprowadził do gry dodatkową regułę: jeśli podana przez Mikołaja liczba jest za mała, Mikołaj musi mu zapłacić 2 zł, a jeśli jest za duża 1 zł (w przypadku trafienia brat nie pobiera opłaty). Wyznacz największe takie N, że Mikołaj może zawsze zgadnąć liczbę brata dysponując budżetem 10 zł.
232
42 J / 42 S
Dodatnie liczby całkowite a, b, c spełniają nierówności a \ge b \ge c oraz równość Znajdź wszystkie możliwe wartości liczby a.
134
43 J / 43 S
Statek kosmitów ma kształt idealnej kuli o promieniu R, podpartej na trzech równoległych pionowych nogach o długości 1\ \text{sk} (sążni kosmickich) i zaniedbywalnej grubości. Dolne końce nóg tworzą trójkąt równoboczny o boku długości 9\ \text{sk}, a gdy statek spoczywa na płaskiej powierzchni, najniższy punkt kuli dokładnie się z nią styka. Ile wynosi R (w \text{sk})?
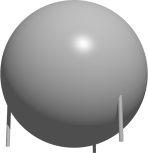
14
44 J / 44 S
Czterej bracia Arek, Bartek, Czarek i Darek zebrali dużą liczbę orzechów pistacjowych. W nocy Arek obudził się z nieodpartą chęcią jedzenia, więc zdecydował się zjeść pewną część orzechów. Policzywszy je, stwierdził, że po odrzuceniu jednego orzeszka, pozostałą część można podzielić na cztery równe części; zjadł więc jeden z orzechów oraz jedną czwartą reszty i wrócił do łóżka. Później tej samej nocy obudził się głodny Bartek i podobnie zjadł jednego orzecha, a następnie czwartą część pozostałych. Do rana to samo przydarzyło się także Czarkowi i Darkowi. Gdy rano bracia spotkali się, zauważyli, że liczba orzechów po odrzuceniu jednego dzieli się przez cztery. Jaka jest najmniejsza liczba orzechów, które mogli zebrać bracia?
1021
45 J / 45 S
Dodatnią liczbę całkowitą nazywamy pistacjową, jeżeli każdy z jej dzielników pierwszych jest równy 2, 3 lub 7. Ile spośród liczb 1000, 1001, \dots, 2000 jest pistacjowych?
19
46 J / 46 S
Imperator Decymus zakazał używania cyfry 0 (wprowadzonej przez jego poprzednika, Nullusa) i wprowadził zamiast niej do użycia cyfrę \mathrm D dla oznaczenia wielkości 10, ustanawiając tym samym notację Decymusa. Każda dodatnia liczba całkowita ma w tej notacji jednoznaczne przedstawienie, np. dotychczas zawierająca 0 liczba 4106 ma nową postać 3\mathrm{DD}6, gdyż Aby ułatwić przejście na nowy system liczbowy, powstała lista wszystkich dodatnich liczb całkowitych od 1 do \mathrm{DDD} (włącznie). Ile razy nowa cyfra \mathrm{D} występuje na tej liście? Liczymy wszystkie wystąpienia, nawet wielokrotne w tej samej liczbie, np. \mathrm{DD} daje dwa wystąpienia \mathrm D.
321
47 J / 47 S
W kwadrat ABCD wpisano okrąg \omega, który jest styczny do boków AB, BC, CD i DA odpowiednio w punktach W, X, Y, Z. Niech E będzie punktem leżącym na krótszym łuku WX okręgu \omega, a F będzie punktem przecięcia prostych BC i EY. Wiedząc, że EF=5 i EY=7, znajdź pole trójkąta FYC.
21
48 J / 48 S
W działaniu każdą cyfrę zastąpiono literą, przy czym takie same cyfry zastąpiono takimi samymi literami, a różne cyfry — różnymi literami. Przy tym wiemy, że \operatorname{S}(W\kern-.1emE)=11, \operatorname{S}(LIKE)=23 oraz \operatorname{S}(N\kern-.2emABOJ)=19, gdzie \operatorname{S}(n) oznacza sumę cyfr liczby n. Żadna z trzech liczb w powyższym działaniu nie może zaczynać się od zera. Wyznacz liczbę N\kern-.2emABOJ.
60\,724
49 J / 49 S
Znajdź wszystkie dodatnie liczby całkowite n, dla których suma wszystkich nietrywialnych dzielników liczby n jest równa 63.
Uwaga. Dzielnik d liczby n nazywamy nietrywialnym, jeżeli 1 < d < n.
56, 76, 122
50 J / 50 S
Beata ma odjazdowy samochód z kwadratowymi tylnymi kołami (przednie są standardowo okrągłe). Taki samochód zwykle nie jest przyjemny do prowadzenia, ale Beata zamontowała bardzo dobry amortyzator do tylnych kół, dzięki któremu podczas jazdy po płaskiej drodze, nadwozie jest cały czas równoległe do drogi oraz nie rusza się kierunku pionowym. Długość boku tylnego koła wynosi 40\ \text{cm} oraz oś tylnych kół nie zmienia pozycji w kierunku poziomym w stosunku do nadwozia. Jaki jest promień przedniego koła (w cm), który powoduje, że kiedy samochód porusza się ze stałą prędkością do przodu (po płaskiej drodze), oś tylnych kół jest dokładnie przez połowę czasu niżej i przez połowę czasu wyżej od osi przednich kół?
10 \sqrt{7}
51 J / 51 S
Miasto Przyszłości ma kształt 2017-kąta foremnego, w którego wierzchołkach rozmieszczonych jest 2017 stacji metra. Na planie miasta są one ponumerowane kolejno liczbami 1, 2, \ldots, 2017 przeciwnie do ruchu wskazówek zegara. W mieście są dwie linie metra: brzegowa i diagonalna. Linia brzegowa zapewnia bezpośrednie połączenie ze stacji a do stacji b (ale nie w przeciwnym kierunku) wtedy i tylko wtedy, gdy a-b+1 jest liczbą podzielną przez 2017. Podróż na każdym takim odcinku trwa 1 minutę. Linia diagonalna obsługuje bezpośrednie połączenie ze stacji a do stacji b wtedy i tylko wtedy, gdy 2b-2a+1 jest liczbą podzielną przez 2017. Podróż na każdym takim odcinku trwa 15 minut. Maciek jest zapalonym użytkownikiem metra i rozpoczynając ze stacji 1 chce on wybrać się w podróż metrem do stacji n o następującej własności: najkrótszy możliwy czas dojazdu metrem do stacji n jest nie krótszy niż najkrótszy możliwy czas dojazdu do którejkolwiek innej stacji. Znajdź wszystkie możliwe numery n docelowych stacji Maćka.
1984, 1985
52 J / 52 S
Niech f(n) oznacza liczbę dodatnich liczb całkowitych, które mają dokładnie n cyfr i których suma cyfr jest równa 5. Ile spośród 2017 liczb całkowitych f(1), f(2), \ldots, f(2017) ma cyfrę jedności równą 1?
202
53 J / 53 S
Rysunek przedstawia dwa podobne sześciokąty wklęsłe, których pewne boki mają odpowiednio długości a, b, c, d oraz A, B, C, D. Układając te dwa sześciokąty obok siebie, jak pokazano na rysunku, uzyskujemy sześciokąt podobny do każdego z nich. Znajdź stosunek A:a.
\sqrt{(1+\sqrt 5)/2}
54 J / 54 S
Wyznacz wszystkie pary dodatnich liczb całkowitych (a,b), dla których wszystkie pierwiastki każdego z równań również są dodatnimi liczbami całkowitymi.
(2,2), (6,6), (7,8), (8,7)
55 J / 55 S
Trójkąt ABC jest wpisany w okrąg \omega, przy czym AB=3, BC=7 oraz AC=5. Dwusieczna kąta BAC przecina bok BC w punkcie D, a okrąg \omega w punkcie E (różnym od A). Niech \gamma będzie okręgiem o średnicy DE, a F — różnym od E punktem przecięcia okręgów \omega i \gamma. Wyznacz długość odcinka AF.
30/\sqrt{19}
56 J / 56 S
Wyznacz liczbę uporządkowanych trójek (x,y,z) nieujemnych liczb całkowitych mniejszych od 2017, dla których liczba jest podzielna przez 2017.
2017^2 + 1 = 4\,068\,290
57 J / 57 S
Ela i Adam używają do gry symetrycznej kostki sześciennej, która ma dwie ściany czerwone, dwie zielone i dwie niebieskie. Na przemian rzucają oni kostką, dopóki któreś z nich nie wyrzuci wszystkich trzech kolorów — ten gracz ogłaszany jest zwycięzcą. Jakie jest prawdopodobieństwo, że Ela wygra, jeżeli jest ona graczem rozpoczynającym?
81/140
58 J / 58 S
Znajdź największą liczbę całkowitą n, dla której istnieje taka liczba całkowita k, że
104
59 J / 59 S
Pizzeria „Obiady Ćwiartkowe” dostarcza pizzę w unikalnych pięciokątnych pudełkach, które są przystosowane zarówno do przewozu ćwiartki dużej pizzy, jak i trzech ćwiartek małej pizzy (jak pokazano na rysunku). Ile wynosi (w \text{cm}) promień małej pizzy, jeżeli promień dużej pizzy jest równy 30 cm?
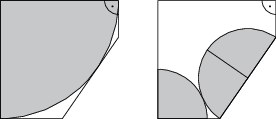
5(1+\sqrt{7}-\sqrt{2\sqrt{7}-4})