1 J
Na obrázku vidíte, ako vyzerajú okná na starých električkách. Všetky oblé rohy sú štvrťoblúky kružnice s polomerom 10\,\text{cm}. Na druhom obrázku je znázornená časť pootvoreného posuvného okna o 10\,\text{cm}. Časť, ktorá sa dá posúvať, má výšku 13\,\text{cm}. Aká je plocha otvorenej časti okna v \text{cm}^2?
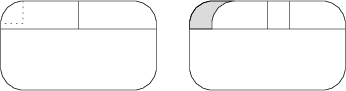
130
2 J
Veľký obdĺžnik je rozdelený na deväť menších obdĺžnikov tak, ako na obrázku. Číslo vpísané v menšom obdĺžniku značí jeho obvod. Nájdite obvod veľkého obdĺžnika.
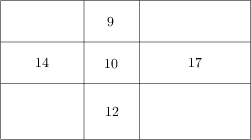
42
3 J
Matej zmazal jednu cifru zo štvorciferného prvočísla a dostal číslo 630. Aké bolo jeho prvočíslo?
6301
4 J
Slávny architekt Leonardo chce postaviť moderný palác s päťuholníkovou základňou na obdĺžnikovom pozemku s rozmermi 35\, \mbox{m} a 25\, \mbox{m}. Umiestniť ho chce presne tak, ako je naznačené na obrázku.
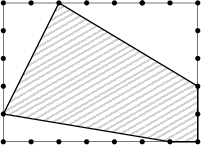
(Bodky na stranách obdĺžnika označujú vzdialenosť 5\,\text{m}.) Vyjadrite zlomkom, akú časť pozemku zaberá základňa paláca.
\frac{41}{70}
5 J
Na obrázku môžete vidieť štvorcovú mriežku pozostávajúcu zo 16 bodov, ktorá obsahuje deväť štvorcov 1\times 1, štyri štvorce 2\times 2 a jeden štvorec 3\times 3, teda celkom 14 štvorcov, ktorých strany sú rovnobežné so stranami mriežky. Aký je najmenší počet bodov, ktorý môžeme odobrať tak, že po ich odobratí bude každému zo 14-tich štvorcov chýbať aspoň jeden vrchol?

4
6 J
Nájdite poslednú cifru súčtu
5
7 J
Vyjadrite podiel ako zlomok \dfrac{a}{b} v základnom tvare, kde a a b sú kladné celé čísla.
Poznámka: Čiara nad číslom znamená desiatkový periodický rozvoj, napr. 0.\overline{123} = 0.123123\ldots.
\frac{11}{12}
8 J
Passau má železničnú stanicu v tvare trojuholníka. Anna, Boris a Cathy pozorujú železničnú dopravu v Linzi, Regensburgu a Waldkirchene na koľajniciach, ktoré prichádzajú z Passau. Anna napočítala 190, Boris 208 a Cathy 72 prichádzajúcich a odchádzajúcich vlakov dokopy. Koľko vlakov prejde z Linzu do Regensburgu alebo opačne, ak žiaden vlak nezačína, nekončí ani nemení smer v Passau?
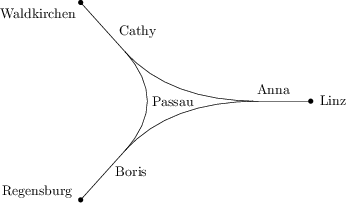
163
9 J
Nájdite všetky kladné celé čísla x < 10\,000 také, že x je štvrtou mocninou nejakého párneho čísla a po permutácii (preusporiadaní) cifier čísla x dostaneme štvrtú mocninu nejakého nepárneho čísla. Číslo po permutácii nemôže začínať nulou.
256
10 J
V rovnobežníku ABCD priamka z bodu C pretne stranu AB v bode E tak, že |EB| =\frac 15\, |AE|. Úsečka CE pretne diagonálu BD v bode F. Zistite pomer |BF| : |BD|.
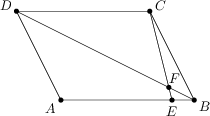
1 : 7
11 J / 11 S
Hotel má 100 očíslovaných izieb. V každej izbe sú jedno, dve alebo tri lôžka. V izbách č. 1 až č. 52 je dokopy 56 lôžok. V izbách č. 51 až č. 100 je dokopy 150 lôžok. Koľko lôžok je dokopy v celom hoteli?
200
12 J / 12 S
V prvom kroku Henka napísala na kúsok papiera červeným perom číslo 3 a zeleným perom číslo 2. V každom z ďalších krokov napísala súčet dvoch čísel z predchádzajúceho kroku červeným perom a ich rozdiel zeleným perom (väčšie z nich mínus menšie). Ktoré číslo napísala Henka červeným perom v 2017-tom kroku?
3 \cdot 2^{1008}
13 J / 13 S
Červená Čiapočka sa cestou k starej mame zatúlala pred „Obdĺžnikový les“. Nachádzala sa v bode A a potrebovala sa dostať do bodu B najrýchlejšie, ako to len ide. Jedna možnosť by bola obísť celý les po jeho okraji, musela by tak prejsť 140\,\text{m}. Samozrejme, Červená Čiapočka pozná trojuholníkovú nerovnosť a vie, že priama cesta by bola kratšia. Nanešťastie, cez les ide iba jedna kľukatá cestička s dvomi pravouhlými zákrutami tak, ako je znázornená na obrázku. Ak je cestička lesom kratšia ako 140\,\text{m}, pôjde ďalej po nej. Zistite dĺžku (v metroch) cestičky cez les.
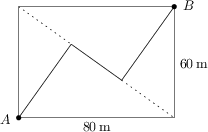
124
14 J / 14 S
Osemmiestny palindróm je číslo, ktoré má tvar \overline{abcddcba}, kde a, b, c a d sú nie nutne rozdielne číslice. O koľkých osemmiestnych palindrómoch platí, že z nich vieme vymazať niektoré číslice tak, že výsledné číslo bude 2017?
8
15 J / 15 S
Pre všetky kladné celé čísla n označíme ich ciferný súčet ako \operatorname S(n) a súčin cifier ako \operatorname P (n). Koľko kladných celých čísel n má vlastnosť n = \operatorname S (n) + \operatorname P (n)?
9
16 J / 16 S
Majiteľ továrne zamestnáva 100 zamestnancov. Každý manažér zarába 5\,000 € za mesiac, každý robotník zarába 1\,000 € za mesiac a každý brigádnik zarába 50 € za mesiac. Majiteľ továrne dokopy platí zamestnancom 100\,000 € za mesiac, pričom zamestnáva aspoň jedného zamestnanca z každého typu. Koľko manažérov pracuje v továrni?
19
17 J / 17 S
Na obrázku vidíte mozaiku zloženú z pravidelných n-uholníkov. Šesťuholník a tmavosivý trojuholník sú vpísané do tej istej kružnice. Každý z troch rovnakých šrafovaných trojuholníkov má obsah 17. Určte obsah tmavosivého trojuholníka.
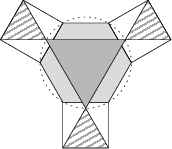
51
18 J / 18 S
V Passau renovujú železničnú stanicu a chcú spraviť aj špeciálny chodník pre nevidiacich. Tvar chodníka je znázornený na obrázku. Nanešťastie majú k dispozícii len dlaždice s rozmermi 1\times 2. Koľkými spôsobmi môžu podľa vzoru položiť chodník? Dlaždice sú nerozlíšiteľné a dve vydláždenia sú rôzne, ak sú aspoň na jednom mieste chodníka dlaždice v rôznych polohách.
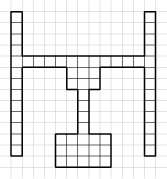
15
19 J / 19 S
Fero si vybral kladné celé číslo n. Potom si vybral kladného deliteľa čísla n, vynásobil ho štyrmi, výsledok odčítal od čísla n a dostal 2017. Nájdite všetky čísla, ktoré si Fero mohol vybrať.
2021, 10085
20 J / 20 S
Denisa a Vanesa sú veľmi dobré kamarátky, takže kedykoľvek sedia vedľa seba začnú spolu klebetiť. Päť študentov (vrátane Denisy a Vanesy) chce mať konštruktívnu diskusiu, takže si chcú posadať na päť stoličiek okolo okrúhleho stola tak, aby Denisa a Vanesa nesedeli vedľa seba. Koľkými možnosťami to dokážu spraviť? Možnosti, ktoré sa líšia otočením, sú rôzne.
60
21 J / 21 S
Ako vidíte na obrázku, AB je priemerom kružnice so stredom M. Dva body D a C sú na kružnici tak, aby platilo AC\perp DM a |\sphericalangle MAC| = 56^\circ. Zistite veľkosť ostrého uhla medzi priamkami AC a BD v stupňoch.
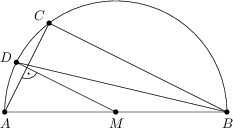
73^\circ
22 J / 22 S
Útvar je poskladaný zo štvorcov s jednotkovým obsahom postupným spájaním jeho kópií, ako je znázornené na obrázku. Aká je dĺžka hrubej hranice útvaru v šiestom kroku?
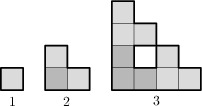
488
23 J / 23 S
Všetkých 2017 sedadiel okolo veľmi veľkého okrúhleho stola je obsadených superhrdinami alebo zloduchmi. Superhrdinovia vždy hovoria pravdu a každý zloduch vždy klame. Každý človek, ktorý sedí za stolom skonštatoval, že sedí medzi superhrdinom a zloduchom. Z neznámeho dôvodu práve jeden superhrdina urobil chybu. Koľko superhrdinov je za stolom?
1345
24 J / 24 S
Nájdite všetky kladné reálne čísla x také, že
\sqrt[2016]{2017}
25 J / 25 S
Leo chce zafarbiť hrany dvanásťstena špeciálnym spôsobom. Vyberie zvýrazňovač jednej farby a začne ľubovoľným vrcholom dvanásťstena. Potom postupuje po hranách bez toho, aby zodvihol zvýrazňovač alebo zafarbil jednu hranu dvakrát, až kým chce alebo je donútený prestať. Potom vezme zvýrazňovač inej farby a začne farbiť nejaké ešte nezafarbené pospájané hrany. Takto pokračuje s ďalšími farbami dovtedy, kým je každá hrana dvanásťstena zafarbená práve jednou farbou. Aký je minimálny počet farieb, ktoré môže použiť?
Dvanásťsten je pravidelné teleso s dvanástimi päťuholníkovými stenami ako je znázornené na obrázku:
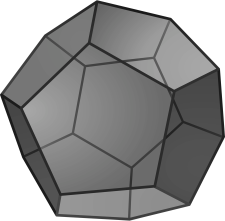
10
26 J / 26 S
Záhradný architekt Jožko navrhol nový štrkový chodníček okolo jazera. Trojuholník ABC predstavuje stred chodníčka so stranami dĺžky a = 80\,\text{m}, b = 100\,\text{m} a c = 120 \,\text{m}. Okraje chodníčka tvoria úsečky, ktoré sú vzdialené 1\,\text{m} od zodpovedajúcich strán trojuholníka ABC, ako môžeme vidieť na obrázku. Koľko \text{m}^3 vysokokvalitného štrku musí Jožko objednať, aby mohol vytvoriť štrkový chodníček s priemernou výškou 4\,\text{cm}?
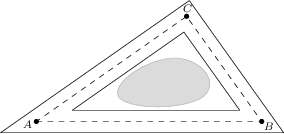
24
27 J / 27 S
Nájdite všetky štvorciferné druhé mocniny celých čísel také, že prvé dve číslice sú rovnaké a posledné dve číslice sú tiež rovnaké.
7744
28 J / 28 S
V lunaparku je jednou z atrakcií aj losovanie lotérie. Pravidlá sú nasledovné: súťažiaci vyberá jednu zo štyroch rôznych krabičiek a potom z nej vytiahne jednu loptičku. Ak je táto loptička biela, súťažiaci vyhráva, a ak je čierna, prehráva. Ak je rozdelenie loptičiek v krabičkách napríklad kde každá dvojica (b, c) označuje krabičku s b bielymi a c čiernymi loptičkami, potom súťažiaci vyhráva s pravdepodobnosťou \frac{5}{8}. Každý 1000-ci súťažiaci dostane superžolíka: Súžažiaci môže prerozdeliť loptičky v krabičkách podľa svojej vôle, pričom do každej krabičky musí dať aspoň jednu loptičku. Potom sa krabičky opäť pomiešajú a súťažiaci vyberá jednu krabičku a z nej jednu loptičku. Jolanka má šťastie a vyhrala superžolíka. Aká je najväčšia pravdepodobnosť výhry, ktorú môže mať po vhodnom prerozdelení loptičiek z príkladu?
\frac{51}{58}
29 J / 29 S
Autobus, nákladiak a motorka sa pohybujú konštantnou rýchlosťou a prechádzajú v tomto poradí okolo stojaceho pozorovateľa v rovnakých časových intervaloch. Ďalej po ceste prejdú okolo ďalšieho pozorovateľa v rovnakých časových intervaloch, ale v inom poradí. Tentokrát v poradí autobus, motorka a nákladiak. Zistite rýchlosť autobusu (v km/h), ak rýchlosť nákladiaka je 60\,\text{km/h} a rýchlosť motorky je 120\,\text{km/h}.
80
30 J / 30 S
Nájdite všetky možnosti, ako možno vyplniť voľné políčka vo výroku nižšie celými číslami tak, aby bol pravdivý.
„V tomto výroku je \boxed{\phantom{00}}\,\% cifier väčších ako 4, \boxed{\phantom{00}}\,\% cifier je menších ako 5 a \boxed{\phantom{00}}\,\% cifier je rovných jednej z dvojice cifier 4 alebo 5.“
50, 50, 60
31 J / 31 S
Paľov dobytok sa pasie na trojuholníkovej lúke ABC. Keďže jeho fľakaté a biele kravy spolu dobre nevychádzajú, Paľo postavil 20-metrový plot kolmý na stranu AC, ktorý začína v bode P na strane AC a končí v bode B. Plot rozdeľuje lúku na dva pravouhlé trojuholníky. Avšak toto rozdelenie nevyhovovalo fľakatým kravám, ktoré sa pasú v oblasti pri bode A. Tie oponovali, že |AP| : |PC| = 2 : 7 a vyžadovali spravodlivejšie delenie. Nakoniec Paľo vymenil plot za druhý, rovnobežný k pôvodnému, ktorý končí na stranách AC a BC. Tento plot rozdeľuje lúku na dve časti s rovnakou plochou. Aká je dĺžka tohto plotu v metroch?
30 \sqrt{\frac27}
32 J / 32 S
Na tabuli je napísaných päť (nie nutne rôznych) reálnych čísel. Pre každé dve z nich Veronika vypočítala ich súčet a napísala desať výsledkov na tabuľu, pričom pôvodných päť čísel vymazala. Určte všetky možné hodnoty súčinu zmazaných čísel.
-144
33 J / 33 S
Napíšte číslo 333 ako súčet ľubovoľného počtu štvorcov (druhých mocnín) rôznych kladných nepárnych celých čísel.
3^2 + 5^2 + 7^2 + 9^2 + 13^2
34 J / 34 S
Eliška si zobrala tri reálne čísla a, b, c a zadefinovala operáciu \odot ako x \odot y = ax + by + cxy. Na precvičenie vyrátala 1 \odot 2 = 3 a 2 \odot 3 = 4. Po ďalšom skúmaní zistila, že existuje nenulové reálne číslo u také, že z \odot u = z pre každé reálne z. Akú hodnotu má u?
4
35 J / 35 S
Tri kružnice s polomerom r a jedna s polomerom 1 sa navzájom dotýkajú podľa obrázku. Nájdite r.
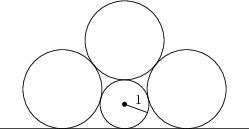
\frac{1+\sqrt{5}}{2}
36 J / 36 S
Na starú betónovú stenu niekto nasprejoval päť (nie nutne rôznych) reálnych čísel, ktorých súčet je 20. Pre každú dvojicu vytvorenú z týchto čísel Harry vypočítal ich súčet a zaokrúhlil ho nadol (t. j. namiesto presného súčtu s zobral najväčšie celé číslo s' neprevyšujúce s). Týmto postupom dostal desať celých čísel. Nakoniec všetky tieto novozískané čísla spočítal. Aký je najmenší možný súčet, ktorý mohol Harry dostať?
72
37 J / 37 S
Máme zložené prirodzené číslo n. Výraz \operatorname{M}(n) označuje súčet troch najmenších deliteľov n a výraz \operatorname{V}(n) označuje súčet dvoch najväčších deliteľov n. Nájdite všetky zložené čísla n, pre ktoré \operatorname{V}(n)=(\operatorname{M}(n))^4.
Poznámka: Za deliteľa daného čísla považujeme aj to samotné číslo.
864
38 J / 38 S
V tabuľke 3 \times 3 sedí myš v ľavom dolnom políčku. Jej úlohou je dostať sa ku kusu syra v pravom hornom políčku, pričom sa môže premiestňovať len na vedľajšie políčko toho, na ktorom práve stojí. Koľkými spôsobmi môžeme vyplniť niektoré (prípadne žiadne) z neobsadených políčok prekážkami tak, aby sa myš stále vedela dostať k syru?
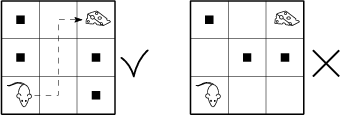
51
39 J / 39 S
Zo všetkých dvojíc reálnych čísel (x, y), ktoré vyhovujú rovnici je (x_0, y_0) to s minimálnou hodnotou x_0. Nájdite y_0.
-3
40 J / 40 S
Trojuholník ABC je pravouhlý s pravým uhlom pri vrchole C. Body D a E ležia na hrane AB, pričom D leží medzi bodmi A a E tak, že úsečky CD a CE delia uhol ACB na tri rovnaké časti. Ak |DE|:|BE| = 8:15, zistite pomer |AC| : |BC|.
\frac{4\sqrt3}{11}
41 J / 41 S
Miško sa hrá nasledovnú hru. Jeho úlohou je nájsť celé číslo medzi 1 a N (vrátane nich). V každom ťahu vyberie celé číslo z tohto intervalu, ak je to správne číslo, hra skončila, inak sa dozvie, či je jeho číslo príliš malé alebo príliš veľké. Avšak, ak je Miškovo číslo príliš veľké, musí zaplatiť 1 €, ak je príliš malé, musí zaplatiť 2 € (neplatí, ak uhádol). Aké je najväčšie celé číslo N také, že Miško vie vždy skončiť hru, pričom minie najviac 10 €?
232
42 J / 42 S
Kladné celé čísla a, b, c spĺňajú a \geq b \geq c a Nájdite všetky možné hodnoty čísla a.
134
43 J / 43 S
Vesmírna loď má tvar presnej gule s polomerom R, pričom je podopretá troma rovnobežnými zvislými piliermi s dĺžkou 1\,\text{vm} (vesmírny meter) a zanedbateľnou hrúbkou. Spodné konce týchto pilierov sa nachádzajú vo vrcholoch rovnostranného trojuholníka s dĺžkou strany 9\,\text{vm}. Keď je vesmírna loď položená na rovnom povrchu, najnižší bod gule sa dotýka povrchu. Ako dlhý je polomer R (v jednotkách \text{vm})?
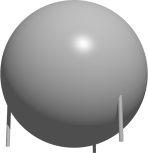
14
44 J / 44 S
Štyria bratia Andrej, Braňo, Cecil a Denis v lese nazbierali veľkú kopu orechov. Uprostred noci sa Andrej zobudil s obrovskou chuťou jesť, takže sa rozhodol zjesť nejaké z orechov, čo nazbierali. Keď ich spočítal, zistil, že keby odobral jeden orech, zvyšok by sa dal rozdeliť na štyri rovnaké časti. Zahodil preč teda jeden orech a zjedol jednu štvrtinu z toho, čo zostalo. Potom šiel znova spať. Neskôr v noci sa kvôli hladu zobudil aj Braňo a znovu zistil, že keď zahodí jeden orech, zvyšok sa bude dať rozdeliť na štvrtiny. Takže ho zahodil a zjedol štvrtinu zvyšku. Do rána sa presne to isté stalo aj Cecilovi a Denisovi. Keď sa všetci ráno zišli, zistili, že počet orechov bol stále deliteľný štyrmi po odstránení jedného orechu. Koľko najmenej orechov mohli mať na začiatku?
1021
45 J / 45 S
Číslo nazývame praktické, ak nemá iné prvočíselné delitele ako 2, 3 a 7. Koľko praktických čísel je medzi číslami 1000,\, 1001,\, \dots,\, 2000?
19
46 J / 46 S
Cisár Decimus zakázal používanie cifry 0 (zavedenej jeho predchodcom Nullusom) a nariadil, aby sa namiesto nej používala cifra \mathrm D, reprezentujúca množstvo 10, a tak zaviedol Decimovu notáciu. Každé prirodzené číslo má stále jednoznačný zápis, napr. Aby sa zjednodušil prechod na nový systém, napísal sa zoznam všetkých čísel od 1 do \mathrm{DDD} (vrátane). Koľko výskytov novej cifry \mathrm D je v zozname? Viacnásobné výskyty v jednom čísle sa počítajú podľa násobnosti, napr. \mathrm{DD} je rátané ako dve \mathrm D-čka.
321
47 J / 47 S
Štvorec ABCD má vpísanú kružnicu \omega, ktorá sa dotýka štvorca v bodoch W, X, Y, Z, ktoré ležia postupne na stranách AB, BC, CD, DA. Nech E je vnútorný bod (kratšieho) oblúku kružnice \omega medzi bodmi W a X a nech F je priesečník priamok BC a EY. Ak vieme, že |EF| = 5 a |EY| = 7, vypočítajte obsah trojuholníka FYC.
21
48 J / 48 S
V algebrograme rôzne písmená zastupujú rôzne číslice. Okrem toho vieme, že \operatorname{S}(W\!E)=11, \operatorname{S}(LIKE)=23 a \operatorname{S}(N\!ABOJ)=19, kde \operatorname{S}(n) označuje ciferný súčet čísla n. Žiadne z týchto čísel nemôže začínať nulou. Nájdite 5-ciferné číslo N\!ABOJ.
60\,724
49 J / 49 S
Nájdite všetky prirodzené čísla n s vlastnosťou, že súčet všetkých netriviálnych deliteľov čísla n je 63.
Poznámka: Netriviálny deliteľ d čísla n spĺňa 1 < d < n.
56, 76, 122
50 J / 50 S
Jožo má štýlové auto so štvorcovými zadnými kolesami (predné kolesá sú štandardné okrúhle). Také auto by sa normálne šoférovalo veľmi nepríjemne, ale Jožo nainštaloval veľmi dobré tlmiče pre zadné kolesá tak, aby auto ostalo v pevnej pozícii rovnobežnej s povrchom počas jazdy na rovnej ceste. Dĺžka strany zadného kolesa je 40\,\text{cm} a jeho náprava je v pevnej pozícii vzhľadom na auto v horizontálnom smere (teda vzhľadom na auto sa hýbe len dohora a dodola). Aký je polomer predného kolesa (v cm), ak vieme, že keď sa auto hýbe konštantnou rýchlosťou dopredu, tak je náprava zadného kolesa presne polovicu času vyššie a polovicu času nižšie nad povrchom ako náprava predného kolesa?
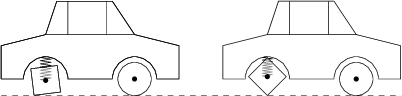
10 \sqrt{7}
51 J / 51 S
Mesto Budúcnosti má tvar pravidelného 2017-uholníka. Vo vrcholoch mesta je 2017 staníc metra, očíslovaných 1,\, 2,\, \ldots,\, 2017 proti smeru hodinových ručičiek. V meste premávajú dve linky metra: stranová a uhlopriečna. Stranová linka zabezpečuje priame spojenie zo stanice a do b (ale nie v opačnom smere) práve vtedy, keď a-b+1 je deliteľné číslom 2017, a jedna taká jazda trvá 1 minútu. Uhlopriečna linka premáva zo stanice a do b práve vtedy, keď 2b-2a+1 je deliteľné číslom 2017, a jedna jazda trvá 15 minút. Mr. Miro je vášnivý cestovateľ metrom a začínajúc zo stanice 1, chce nájsť cestu do stanice n s nasledujúcou vlastnosťou: Najkratší možný čas potrebný na to, aby sme sa dostali metrom do tejto stanice, je najväčší medzi všetkými stanicami. Nájdite všetky hodnoty n možných cieľových staníc pre Mr. Mira.
1984, 1985
52 J / 52 S
Nech f(n) je počet prirodzených čísel, ktoré majú presne n cifier a ktorých cifry majú súčet 5. Určte, koľko z 2017 prirodzených čísel f(1),\, f(2),\, \dots,\, f(2017) má cifru na mieste jednotiek rovnú 1.
202
53 J / 53 S
Na obrázku sú dva (nepriamo) podobné šesťuholníky, ktorých niektoré zo strán majú dĺžku a, b, c, d a A, B, C, D. Ak ich dáme dohromady tak, ako na obrázku, dostaneme nový šesťuholník, ktorý je s nimi tiež podobný (priamo podobný tomu napravo). Nájdite pomer A : a.
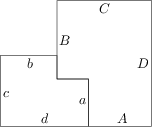
\sqrt{\frac{1+\sqrt 5}{2}}
54 J / 54 S
Nájdite všetky dvojice prirodzených čísel (a,b), pre ktoré sú všetky korene oboch rovníc tiež prirodzené čísla.
(2,2), (6,6), (7,8), (8,7)
55 J / 55 S
Trojuholník ABC s |AB| = 3, |BC| = 7, a |AC| = 5 je vpísaný do kružnice \omega. Os uhla BAC pretína stranu BC v bode D a kružnicu \omega po druhýkrát v bode E. Nech \gamma je kružnica s priemerom DE. Kružnice \omega a \gamma sa pretínajú v bodoch E a F. Určte dĺžku úsečky AF.
\frac{30}{\sqrt{19}}
56 J / 56 S
Určte počet usporiadaných trojíc (x, y, z), kde x, y, z sú nezáporné celé čísla menšie ako 2017 také, že výraz je deliteľný číslom 2017.
2017^2 + 1 = 4\,068\,290
57 J / 57 S
Slavo a Pedro hrajú hru so spravodlivou kockou, ktorá má dve červené steny, dve zelené a dve modré. Striedavo hádžu kockou, až dokým jeden z nich neuvidí pri svojich hodoch všetky tri farby na vrchu kocky. Ten hráč, ktorému sa to podarí, sa stáva víťazom. S akou pravdepodobnosťou Slavo vyhrá, za predpokladu, že on je prvý, ktorý hádže kockou?
81/140
58 J / 58 S
Pre danú rovnicu nájdite najväčšie celé číslo n, pre ktoré existuje celočíselné riešenie tejto rovnice (k, n).
104
59 J / 59 S
Pizzéria Štvrť roznáša pizze v špeciálnych päťuholníkových škatuliach, ktoré sú vhodné aj pre štvrtinu veľkej pizze, aj pre tri štvrtiny malej pizze (ako na obrázku). Aký je polomer malej pizze (v cm), ak polomer veľkej pizze je 30 cm?
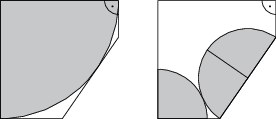
5(1+\sqrt{7}-\sqrt{2\sqrt{7}-4})






















